Cluster Analysis Mark Stamp Cluster Analysis 1 Cluster































































- Slides: 70

Cluster Analysis Mark Stamp Cluster Analysis 1

Cluster Analysis q Grouping objects in meaningful way o Clustered data fits together in some way o Can help to make sense of (big) data o Finds application in many fields q Many different clustering strategies q Overview, then details on 2 methods o K-means simple and can be effective o EM clustering not as simple Cluster Analysis 2

Intrinsic vs Extrinsic q Intrinsic clustering relies on unsupervised learning o No predetermined labels on objects o Apply analysis directly to data q Extrinsic requires category labels o Requires pre-processing of data o Can be viewed as a form of supervised learning Cluster Analysis 3

Agglomerative vs Divisive q Agglomerative o Each object starts in its own cluster o Clustering merges existing clusters o A “bottom up” approach q Divisive o All objects start in one cluster o Clustering process splits existing clusters o A “top down” approach Cluster Analysis 4

Hierarchical vs Partitional q Hierarchical clustering o “Child” and “parent” clusters o Can be viewed as dendrograms q Partitional clustering o Partition objects into disjoint clusters o No hierarchical relationship q We consider K-means and EM in detail o These are both partitional Cluster Analysis 5

Hierarchical Clustering q Example 1. 2. of a hierarchical approach. . . start: Every point is its own cluster while number of clusters exceeds 1 o Find 2 nearest clusters and merge end while q OK, but no real theoretical basis 3. o And some find that “disconcerting” o Even K-means has some theory behind it Cluster Analysis 6

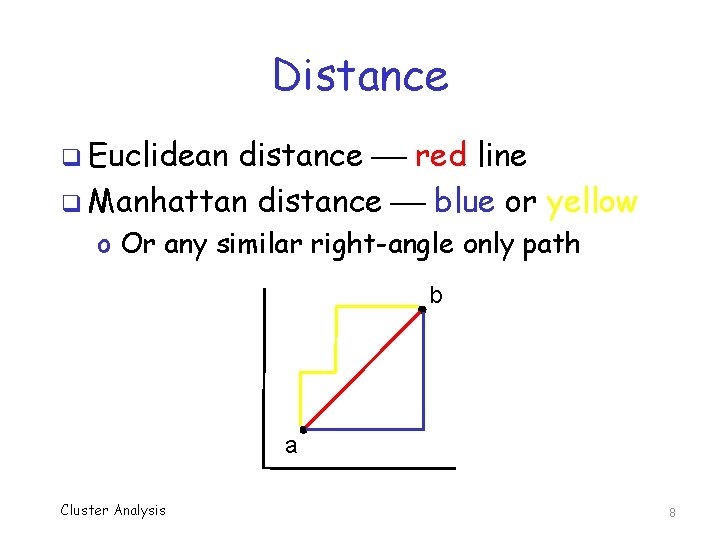
Distance q Distance between data points? q Suppose x = (x 1, x 2, …, xn) and y = (y 1, y 2, …, yn) where each xi and yi are real numbers q Euclidean distance is d(x, y) = sqrt((x 1 -y 1)2 + (x 2 -y 2)2 +…+ (xn-yn)2) q Manhattan (taxicab) distance is d(x, y) = |x 1 -y 1| + |x 2 -y 2| + … + |xn-yn| Cluster Analysis 7

Distance q Euclidean distance red line q Manhattan distance blue or yellow o Or any similar right-angle only path b a Cluster Analysis 8

Distance q Lots and lots more distance measures q Other examples include o Mahalanobis distance takes mean and covariance into account o Simple substitution distance measure of “decryption” distance o Chi-squared distance statistical o Or just about anything you can think of… Cluster Analysis 9

One Clustering Approach q Given data points x 1, x 2, x 3, …, xm q Want to partition into K clusters o I. e. , each point in exactly one cluster q. A centroid specified for each cluster o Let c 1, c 2, …, c. K denote current centroids q Each xi associated with one centroid o Let centroid(xi) be centroid for xi o If cj = centroid(xi), then xi is in cluster j Cluster Analysis 10

Clustering q Two crucial questions 1. How to determine centroids, cj? 2. How to determine clusters, that is, how to assign xi to centroids? q But first, what makes a cluster good? o For now, focus on one individual cluster o Relationship between clusters later… q What Cluster Analysis do you think? 11

Distortion q Intuitively, “compact” clusters good o Depends on data and K, which are given o And depends on centroids and assignment of xi to clusters (which we can control) q How to measure this “goodness”? q Define distortion = Σ d(xi, centroid(xi)) o Where d(x, y) is a distance measure q Given Cluster Analysis K, let’s try to minimize distortion 12

Distortion q Consider this 2 -d data o Choose K = 3 clusters q Same data for both o Which has smaller distortion? q How to minimize distortion? o Good question… Cluster Analysis 13

Distortion q Note, distortion depends on K o So, should probably write distortion. K q Typically, larger K, smaller distortion. K o Want to minimize distortion. K for fixed K q Best choice of K is a different issue o Briefly considered later o Also consider other measures of goodness q For now, assume K is given and fixed Cluster Analysis 14

How to Minimize Distortion? Given m data points and K … q Min distortion via exhaustive search? q o Try all m choose K different cases? o Too much work for realistic size data set q An approximate solution will have to do o Exact solution is NP-complete problem q Important Note: For minimum distortion… o Each xi grouped with nearest centroid o Centroid must be center of its group Cluster Analysis 15

K-Means q Previous slide implies that we can improve suboptimal cluster by either… 1. Re-assign each xi to nearest centroid 2. Re-compute centroids so they’re centered q No improvement from applying either 1 or 2 more than once in succession q But alternating might be useful o In fact, that is the K-means algorithm Cluster Analysis 16

K-Means Algorithm q Given 1. 2. 3. 4. 5. dataset… Select a value for K (how? ) Select initial centroids (how? ) Group data by nearest centroid Recompute centroids (cluster centers) If significant change, goto 3; else stop Cluster Analysis 17

K-Means Animation q Very good animation here http: //shabal. in/visuals/kmeans/2. html q Nice animations of movement of centroids in different cases here http: //www. ccs. neu. edu/home/kenb/db/examples/059. html (near bottom of web page) q Other? Cluster Analysis 18

K-Means q Are we assured of optimal solution? o Definitely not q Why not? o For one thing, initial centroid locations are critical o There is a (sensitive) dependence on initial conditions o This is a common issue in iterative processes (HMM training, is an example) Cluster Analysis 19

K-Means Initialization q Recall, K is the number of clusters q How to choose K? q No obvious “best” way to do so q But K-means is fast o So trial and error may be OK o That is, experiment with different K o Similar to choosing N in HMM q Is there a better way to choose K? Cluster Analysis 20

Optimal K? q Even for trial and error, need a way to measure “goodness” of results q Choosing optimal K is tricky q Most intuitive measures will tend to improve for larger K q But K “too big” may overfit data q So, when is K “big enough”? o But not too big… Cluster Analysis 21

Schwarz Criterion q f(K) Choose K that minimizes K f(K) = distortion. K + λd. K log m o Where d is the dimension, m is the number of data points, and λ is ? ? ? q Recall that distortion depends on K o Tends to decrease as K increases o Essentially, adding a penalty as K increases q Related to Bayes Information Criterion (BIC) o And some other similar things q Consider choice of K in more detail later… Cluster Analysis 22

K-Means Initialization q How to choose initial centroids? q Again, no best way to do this o Counterexamples to any “best” approach q Often just choose at random q Or uniform/maximum spacing o Or some variation on this idea q Other? Cluster Analysis 23

K-Means Initialization q In practice, often… q Try several different choices of K o For each K, test several initial centroids q Select the result that is best o How to measure “best”? o We’ll look at that next q May not be very scientific o But often works well Cluster Analysis 24

K-Means Variations q K-mediods o Centroids point must be actual data point q Fuzzy K-means o In K-means, any data point is in one cluster and not in any other o In fuzzy case, data point can be partly in several different clusters o “Degree of membership” vs distance q Many Cluster Analysis other variations… 25

Measuring Cluster Quality q How can we judge clustering results? o In general, that is, not just for K-means q Compare o o to typical training/scoring… Suppose we test new scoring method E. g. , score malware and benign files Compute ROC curves, AUC, etc. Many tools to measure success/accuracy q Clustering Cluster Analysis is different (Why? How? ) 26

Clustering Quality q Clustering is a fishing expedition o Not sure what we are looking for o Hoping to find structure, data discovery o If we know answer, no point to clustering q Might find something that’s not there o Even random data can be clustered q Some things to consider on next slides o Relative to the data to be clustered Cluster Analysis 27

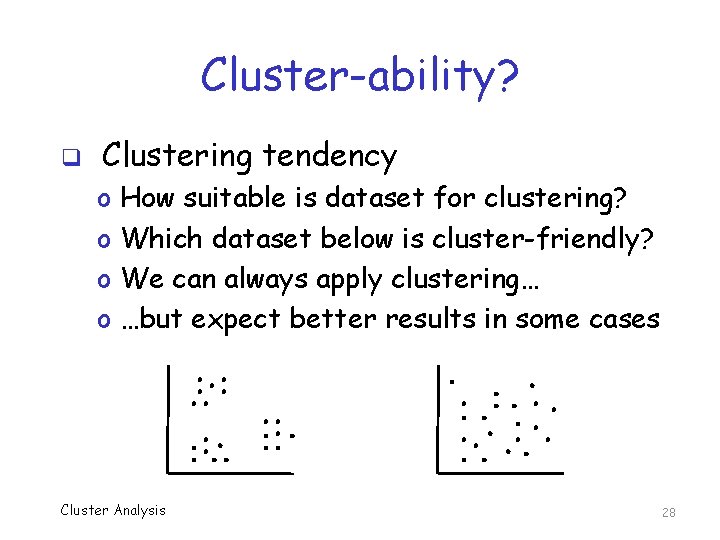
Cluster-ability? q Clustering tendency o o How suitable is dataset for clustering? Which dataset below is cluster-friendly? We can always apply clustering… …but expect better results in some cases Cluster Analysis 28

Validation q External validation o Compare clusters based on data labels o Similar to usual training/scoring scenario o Good idea if know something about data q Internal validation o Determine quality based only on clusters o E. g. , spacing between and within clusters o Generally applicable Cluster Analysis 29

It’s All Relative q Comparing clustering results o That is, compare one clustering result with others for same dataset o Would be very useful in practice o Often, lots of trial and error o Could enable us to “hill climb” to better clustering results… o …if we have a way to quantify things Cluster Analysis 30

How Many Clusters? q Optimal number of clusters? o o o Already mentioned this wrt K-means But what about the general case? I. e. , no reference to clustering technique Can the data tell us how many clusters? Or the topology of the clusters? q Next, we consider several relevant measures Cluster Analysis 31

Internal Validation q Direct measurement of clusters o Might call it “topological” validation q We’ll o o o consider the following Cluster correlation Similarity matrix Sum of squares error Cohesion and separation Silhouette coefficient Cluster Analysis 32

Cluster Correlation q Given data x 1, x 2, …, xm, and clusters, define 2 matrices q Distance matrix D = {dij} o Where dij is distance between xi and xj q Adjacency matrix A = {aij} o Where aij is 1 if xi and xj in same cluster o And aij is 0 otherwise q Now what? Cluster Analysis 33

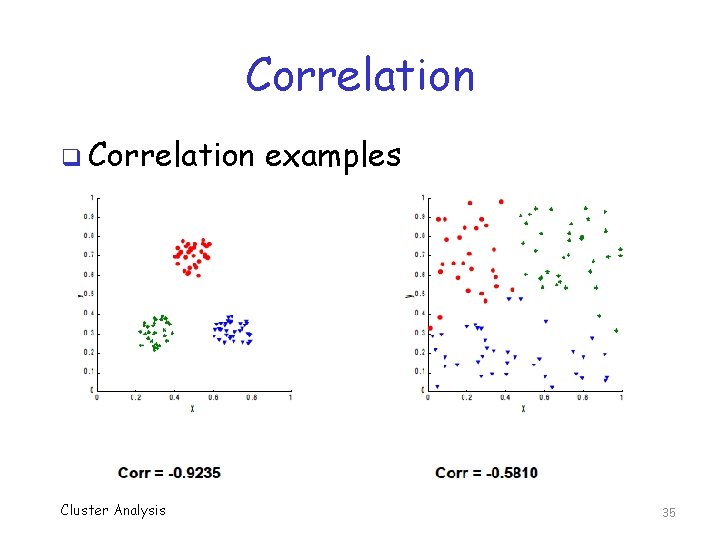
Cluster Correlation q Compute correlation between D and A r. AD = Corr(A, D) = cov(A, D) / (σAσD) = Σ(aij–μA)(dij–μD) / sqrt(Σ(aij–μA)2Σ(dij–μD)2) q Can show that r is between -1 and 1 o If r > 0 then positive Corr (and vice versa) o Magnitude is strength of correlation q High (inverse) correlation implies nearby things clustered together Cluster Analysis 34

Correlation q Correlation Cluster Analysis examples 35

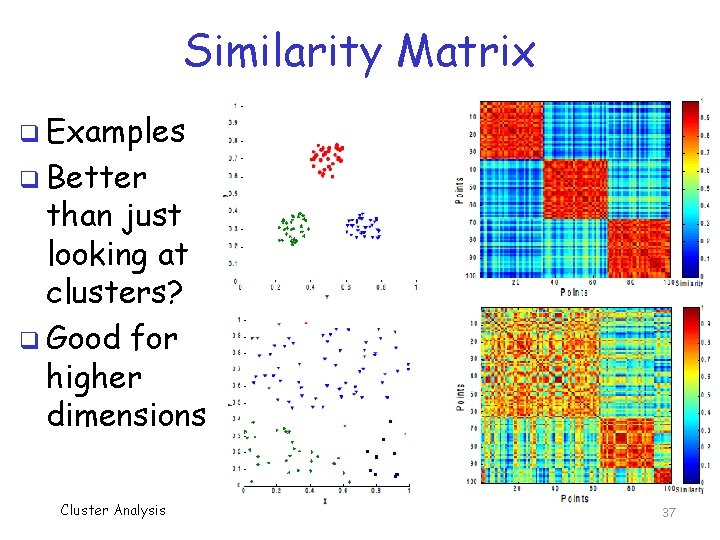
Similarity Matrix q Form “similarity matrix” o Could be based on just about anything o Typically, distance matrix D = {dij}, where dij = d(xi, xj) q Group rows and columns by cluster q Heat map for resulting matrix o Provides visual representation of similarity within clusters (so look at it…) Cluster Analysis 36

Similarity Matrix q Examples q Better than just looking at clusters? q Good for higher dimensions Cluster Analysis 37

Residual Sum of Squares q Residual Sum of Squares (RSS) o Aka Sum of Squared Errors (SSE) o RSS is squared sum of “error” terms o Definition of error depends on problem q What is “error” when clustering? o Distance from centroid? o Then same as distortion o But, could use other measures instead Cluster Analysis 38

Cohesion and Separation q Cluster cohesion o How tightly packed is a cluster o More cohesive clusters is more better q Cluster separation o Distance between clusters o The more separation, the better q Can we measure these things? o Yes, easily Cluster Analysis 39

Notation q Same notation is K-means o Let ci, i=1, 2, …, K, cluster centroids o Let x 1, x 2, …, xm be data points o Let centroid(xi) be centroid of xi o Clusters determined by centroids q Following results apply generally o Not just for K-means… Cluster Analysis 40

Cohesion q Lots of measures of cohesion o Previously defined distortion is useful o Recall, distortion = Σ d(xi, centroid(xi)) q Can also use distance between all pairs Cluster Analysis 41

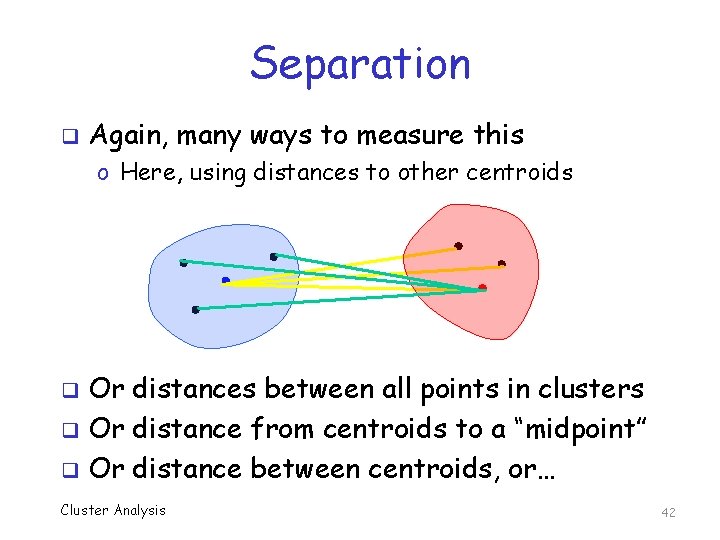
Separation q Again, many ways to measure this o Here, using distances to other centroids Or distances between all points in clusters q Or distance from centroids to a “midpoint” q Or distance between centroids, or… q Cluster Analysis 42

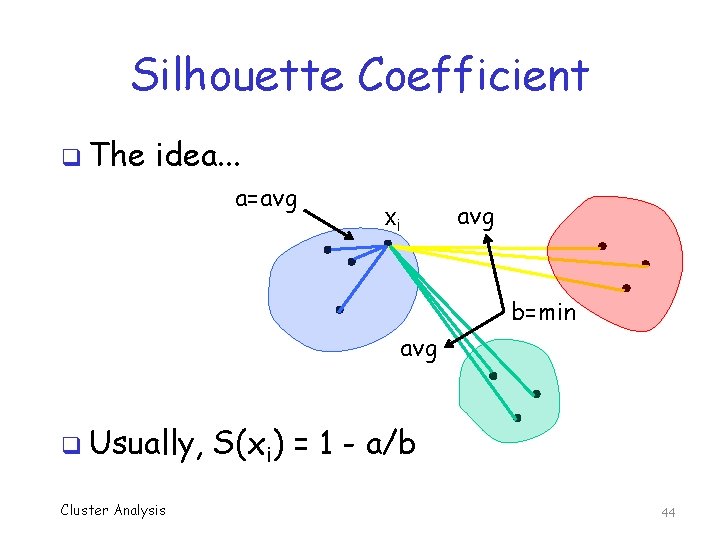
Silhouette Coefficient q Essentially, combines cohesion and separation into a single number q Let Ci be cluster of point xi o Let a be average of d(xi, y) for all y in Ci o For Cj ≠ Ci, let bj be avg d(xi, y) for y in Cj o Let b be minimum of bj q Then let S(xi) = (b – a) / max(a, b) o What the … ? Cluster Analysis 43

Silhouette Coefficient q The idea. . . a=avg xi avg b=min avg q Usually, Cluster Analysis S(xi) = 1 - a/b 44

Silhouette Coefficient q For given point xi, we o Let a be avg distance to points in its cluster o Let b be dist to nearest other cluster (in a sense) Usually, a < b and hence S(xi) = 1 – a/b q If a is a lot less than b, then S(xi) ≈ 1 q o Points inside cluster much closer together than nearest other cluster (this is good) q If a is almost same as b, then S(xi) ≈ 0 o Some other cluster is almost as close as things inside cluster (this is bad) Cluster Analysis 45

Silhouette Coefficient q Silhouette coefficient is defined for each point q Avg silhouette coefficient for a cluster o Measure of how good a cluster is q Avg silhouette coefficient for all points o Measure of clustering “goodness” q What is a good number for coefficient? o Rule of thumb on next slide Cluster Analysis 46

Silhouette Coefficient q Average o o coefficient (to 2 decimal places) 0. 71 to 1. 00 strong structure found 0. 51 to 0. 70 reasonable structure found 0. 26 to 0. 50 weak or artificial structure 0. 25 or less no significant structure q Bottom line on silhouette coefficient o Combine cohesion, separation in one number o One of most useful measures of quality Cluster Analysis 47

External Validation q “External” implies that we measure quality based on data in clusters o Not relying on cluster topology (“shape”) q Suppose clustering data is of several different types o Say, different malware families q We can compute statistics on clusters o We only consider 2 stats here Cluster Analysis 48

Entropy and Purity q Entropy o Standard measure of uncertainty or randomness o High entropy implies clusters less uniform q Purity o Another measure of uniformity o Ideally, cluster should be more “pure”, that is, more uniform Cluster Analysis 49

Entropy q Suppose total of m data elements o As usual, x 1, x 2, …, xm q Denote cluster j as Cj o Let mj be number of elements in Cj o Let mij be count of type i in cluster Cj q Compute probabilities based on relative frequencies o That is, pij = mij / mj Cluster Analysis 50

Entropy q Then entropy of cluster Cj is Ej = − Σ pij log pij, where sum is over i q Compute entropy Ej for each cluster Cj q Overall (weighted) entropy is then E = Σ mj/m Ej, where sum is from 1 to K and K is number of clusters q Smaller E is better o Implies clusters less uncertain/random Cluster Analysis 51

Purity q Ideally, each cluster is all one type q Using same notation as in entropy… o Purity of Cj defined as Uj = max pij o Where max is over i (i. e. , different types) q If Uj is 1, then Cj all one type of data o If Uj is near 0, no dominant type q Overall (weighted) purity is U = Σ mj/m Uj, where sum is from 1 to K Cluster Analysis 52

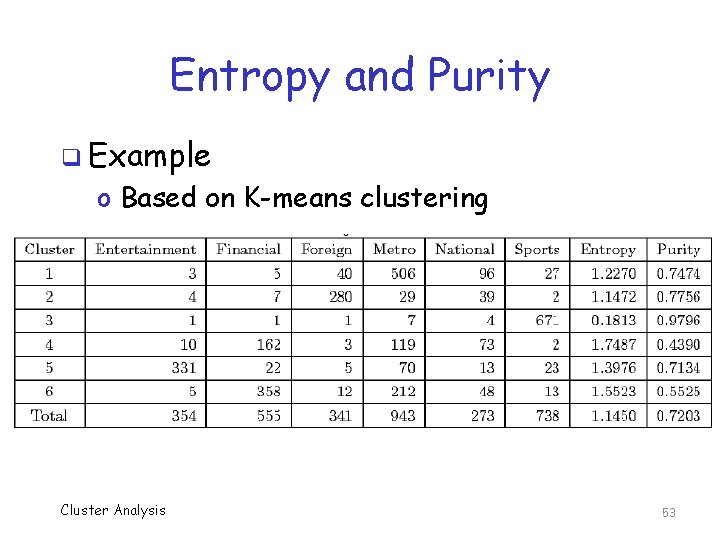
Entropy and Purity q Example o Based on K-means clustering Cluster Analysis 53

EM Clustering q Data might be from different probability distributions o If so, “distance” might be poor measure o Maybe better to use mean and variance q Cluster on probability distributions? o But distributions are unknown… q Expectation maximization (EM) o Technique to determine unknown parameters of probability distributions Cluster Analysis 54

EM Clustering Animation q Good animation on Wikipedia page http: //en. wikipedia. org/wiki/Expectation–maximization_algorithm q Another animation here http: //www. cs. cmu. edu/~alad/em/ q Probably Cluster Analysis others too… 55

Coin Experiment q Given 2 biased coins, A and B o Randomly select coin o Flip selected coin 10 times o Repeat 5 times, so 50 total coin flips q Can we determine P(H) for each coin? q Easy, if you know which coin selected o For each coin, just divide number of heads by number of flips of that coin Cluster Analysis 56

Coin Example q For example, suppose Coin B: HTTTHHTHTH Coin A: HHHHTHHHHH Coin A: HTHHHHHTHH Coin B: HTHTTTHHTT Coin A: THHHTH q Then 5 H and 5 T 9 H and 1 T 8 H and 2 T 4 H and 6 T 7 H and 3 T maximum likelihood estimate is PA(H) = 24/30 = 0. 80 and PB(H) = 9/20 = 0. 45 Cluster Analysis 57

Coin Example q Suppose we have same data, but we do not know which coin was selected Coin ? : 5 Coin ? : 9 Coin ? : 8 Coin ? : 4 Coin ? : 7 q Can H and 5 T H and 1 T H and 2 T H and 6 T H and 3 T we estimate PA(H) and PB(H)? Cluster Analysis 58

Coin Example q We do not know which coin was flipped q So, there is “hidden” information o This should sound familiar… q Train HMM on sequence of H and T ? ? o Using 2 hidden states o Use resulting model to find most likely state sequence (recall, problem 2) o Use sequence to estimate PA(H) and PB(H) Cluster Analysis 59

Coin Example q HMM is very “heavy artillery” o And HMM needs lot of data to converge (or lots of different initializations) o No need to work so hard here q EM algorithm o Alternate between following 2 steps… o Expectation: Recompute expected values o Maximization: Recompute max likelihood Cluster Analysis 60

EM for Coin Example q Start with a guess (initialization) o Say, PA(H) = 0. 6 and PB(H) = 0. 5 q Compute expectations (E-step) q First, from current PA(H) and PB(H) 5 H, 5 T 9 H, 1 T 8 H, 2 T 4 H, 6 T 7 H, 3 T Cluster Analysis P(A) =. 45, P(B) =. 55 P(A) =. 80, P(B) =. 20 P(A) =. 73, P(B) =. 27 P(A) =. 35, P(B) =. 65 P(A) =. 65, P(B) =. 35 61

E-step for Coin Example q So far, we have 5 H, 5 T 9 H, 1 T 8 H, 2 T 4 H, 6 T 7 H, 3 T P(A) =. 45, P(B) =. 55 P(A) =. 80, P(B) =. 20 P(A) =. 73, P(B) =. 27 P(A) =. 35, P(B) =. 65 P(A) =. 65, P(B) =. 35 Next, compute expected (weighted) H and T q For example, in 1 st line q o For A we have 5 x. 45 = 2. 25 H and T o For B we have 5 x. 55 = 2. 75 H and T Cluster Analysis 62

E-step for Coin Example q So far, we have 5 H, 5 T 9 H, 1 T 8 H, 2 T 4 H, 6 T 7 H, 3 T P(A) =. 45, P(B) =. 55 P(A) =. 80, P(B) =. 20 P(A) =. 73, P(B) =. 27 P(A) =. 35, P(B) =. 65 P(A) =. 65, P(B) =. 35 Compute expected (weighted) H and T q For example, in 2 nd line q o For A, we have 9 x. 8 = 7. 2 H and 1 x. 8 =. 8 T o For B, we have 9 x. 2 = 1. 8 H and 1 x. 2 =. 2 T Cluster Analysis 63

E-step for Coin Example q Rounded to nearest 0. 1: Coin A 5 H, 5 T 9 H, 1 T 8 H, 2 T 4 H, 6 T 7 H, 3 T P(A) =. 45, P(B) =. 55 P(A) =. 80, P(B) =. 20 P(A) =. 73, P(B) =. 27 P(A) =. 35, P(B) =. 65 P(A) =. 65, P(B) =. 35 2. 2 H 2. 2 T 7. 2 H 0. 8 T 5. 9 H 1. 5 T 1. 4 H 2. 1 T 4. 5 H 1. 9 T Coin B 2. 8 H 2. 8 T 1. 8 H 0. 2 T 2. 1 H 0. 5 T 2. 6 H 3. 9 T 2. 5 H 1. 1 T totals 21. 2 H 8. 5 T 11. 8 H 8. 5 T q This completes E-step q Note: We computed these expected numbers based on current PA(H) and PB(H) Cluster Analysis 64

M-step for Coin Example q M-step q Re-estimate PA(H) and PB(H) using results from E-step: PA(H) = 21. 2/(21. 2+8. 5) ≈ 0. 71 PB(H) = 11. 8/(11. 8+8. 5) ≈ 0. 58 q Next? E-step using these probabilities o Then M-step, then E-step, then… o …until convergence (or we get tired) Cluster Analysis 65

EM for Clustering q How is EM relevant to clustering? q Can use EM to obtain parameters of K “hidden” distributions o That is, means and variances, μi and σi 2 q Then, use μi as centers of clusters o And σi (standard deviations) as “radii” o Assume Gaussian (normal) distributions q Is this better than K-means? Cluster Analysis 66

EM vs K-Means q Whether it is better or not, EM is obviously different than K-means… o …or is it? q Actually, K-means is special case of EM o Using distance instead of probabilities q E-step? Re-assign points to centroids o Like “E” in EM, this “re-shapes” clusters q M-step? Cluster Analysis Recompute centroids 67

Conclusion q Clustering is fun, entertaining, very useful o Can explore mysterious data, and more… q And K-means is really simple o EM is powerful and not too difficult either q Measuring success is not so easy o Good clusters? And useful information? o Or just random noise? Can cluster anything… q Clustering is often a good starting point o Help us decide whether any “there” is there Cluster Analysis 68

References: K-Means A. W. Moore, K-means and hierarchical clustering q P. -N. Tan, M. Steinbach, and V. Kumar, Introduction to Data Mining, Addison-Wesley, 2006, Chapter 8, Cluster analysis: Basic concepts and algorithms q R. Jin, Cluster validation q M. J. Norusis, IBM SPSS Statistics 19 Statistical Procedures Companion, Chapter 17, Cluster analysis q Cluster Analysis 69

References: EM Clustering C. B. Do and S. Batzoglou, What is the expectation maximization algorithm? , Nature Biotechnology, 26(8): 897 -899, 2008 q J. A. Bilmes, A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models, ICSI Report TR-97 -021, 1998 q Cluster Analysis 70