GAS LAWS Kinetic Molecular Theory Particles in an

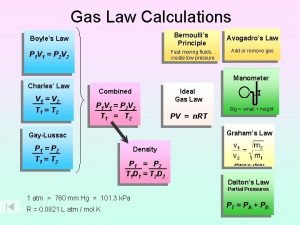
GAS LAWS

Kinetic Molecular Theory • Particles in an ideal gas… – have no volume. – have elastic collisions. – are in constant, random, straight line motion. – don’t attract or repel each other. – have an average KE directly related to Kelvin temperature.

Real Gases • Particles in a REAL gas… – have their own volume – attract and repel each other • Gas behavior is most ideal… – at low pressures – at high temperatures ***Most real gases act like ideal gases except under high pressure and low temperature.

Characteristics of Gases • Gases expand to fill any container. – Take the shape and volume of their container. • Gases are fluids (like liquids). – Little to no attraction between the particles • Gases have very low densities. = lots of empty space between the particles

Characteristics of Gases • Gases can be compressed. – lots of empty space between the particles – Indefinite density • Gases undergo diffusion. – random motion – scatter in all directions

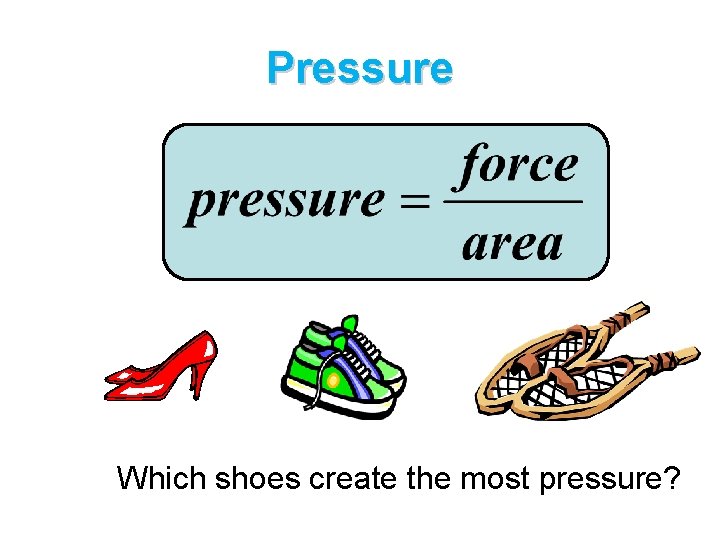
Pressure Which shoes create the most pressure?

Pressure how much a gas is pushing on a container. • Atmospheric pressure atmospheric gases push on everything on Earth • UNITS AT SEA LEVEL 1 atm =101. 3 k. Pa (kilopascal)= 760 mm. Hg =760 torr

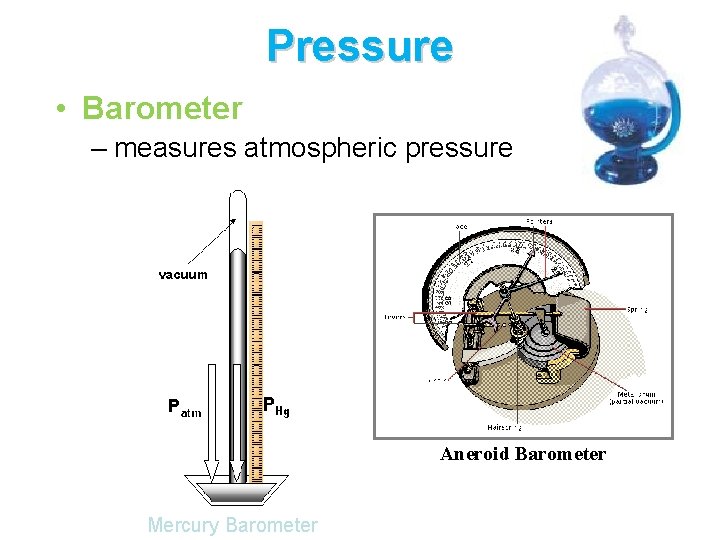
Pressure • Barometer – measures atmospheric pressure Aneroid Barometer Mercury Barometer

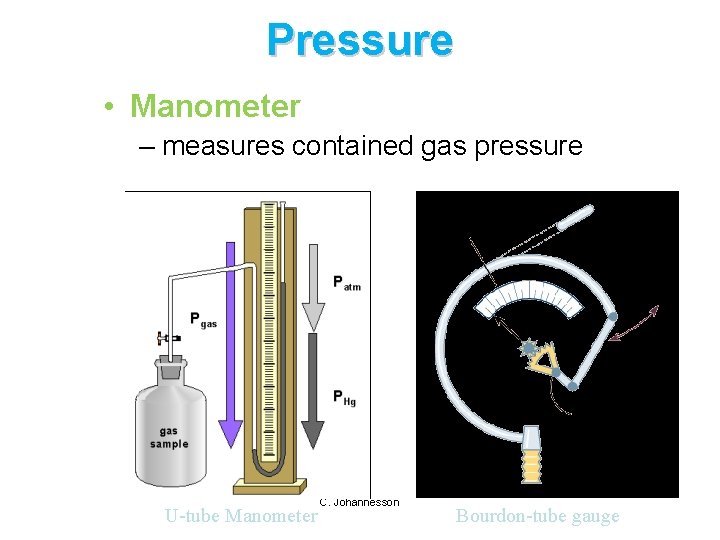
Pressure • Manometer – measures contained gas pressure U-tube Manometer C. Johannesson Bourdon-tube gauge

Temperature= how fast the molecules are moving • Always use absolute temperature (Kelvin) when working with gases. ºF -459 ºC -273 K 0 32 212 0 100 273 373 K = ºC + 273 C. Johannesson

STP Standard Temperature & Pressure 0°C 1 atm -OR- 273 K -OR- 101. 3 k. Pa 760 mm Hg

Volume = how much space a gas occupies Units – L, m. L, cm 3 • 1000 m. L = 1 L • 1 m. L = 1 cm 3

BASIC GAS LAWS

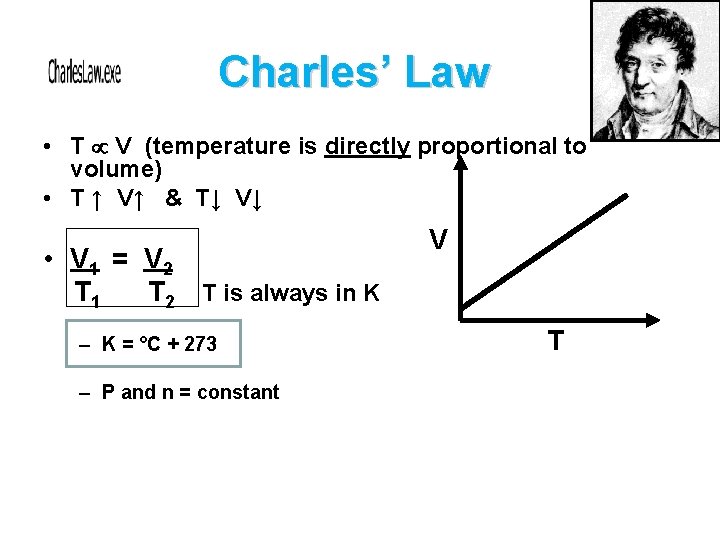
Charles’ Law • T V (temperature is directly proportional to volume) • T ↑ V↑ & T↓ V↓ • V 1 = V 2 T 1 T 2 T is always in K – K = °C + 273 – P and n = constant V T

Charles’ Law V 1 V 2 = T 1 T 2 (Pressure is held constant) Timberlake, Chemistry 7 th Edition, page 259

Timberlake, Chemistry 7 th Edition, page 254

Charles’ Law The egg out of the bottle Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Charles’ Law Problem • Mrs. Rodriguez inflates a balloon for a party. She is in an airconditioned room at 27. 0 o. C, and the balloon has a volume of 4. 0 L. Because she is a curious and intrepid chemistry teacher, she heats the balloon to a temperature of 57. 0 o. C. What is the new volume of the balloon if the pressure remains constant? Given Unkown T 1 = 27. 0 o. C +273= 300 K V = ? L 2 V 1 = 4. 0 L T 2 = 57. 0 o. C +273= 330 K Substitute and Solve 4. 0 L = V 2 = 300 K 330 K 4. 4 L Equation P 1 V 1 = P 2 V 2 T 1 V 1 T 2

Charles’ Law Learning Check • A 25 L balloon is released into the air on a warm afternoon (42º C). The next morning the balloon is recovered on the ground. It is a very cold morning and the balloon has shrunk to 22 L. What is the temperature in º C? Given Unkown V 1 = 25 L T 2 = ? ºC T 1 = 42 o. C +273= 315 K V 2 = 22 L Equation P 1 V 1 = P 2 V 2 T 1 V 1 T 2 Substitute and Solve 25 L = 22 L = 315 K T 2 277. 2 K -273 = 4. 2 ºC

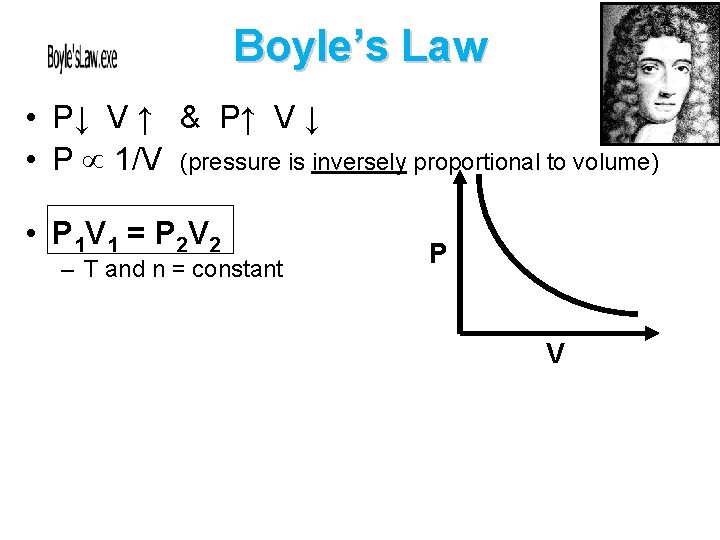
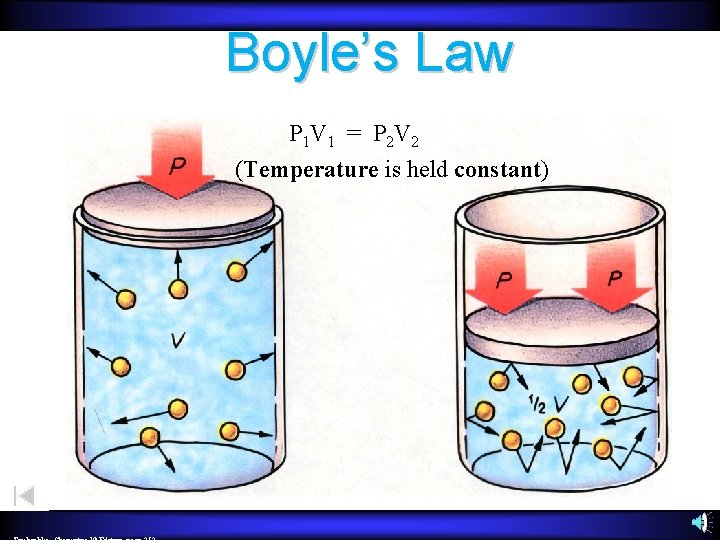
Boyle’s Law • P↓ V ↑ & P↑ V ↓ • P 1/V (pressure is inversely proportional to volume) • P 1 V 1 = P 2 V 2 – T and n = constant P V

Boyle’s Law P 1 V 1 = P 2 V 2 (Temperature is held constant)

Boyle’s Law Marshmallows in a vacuum Timberlake, Chemistry 7 th Edition, page 254

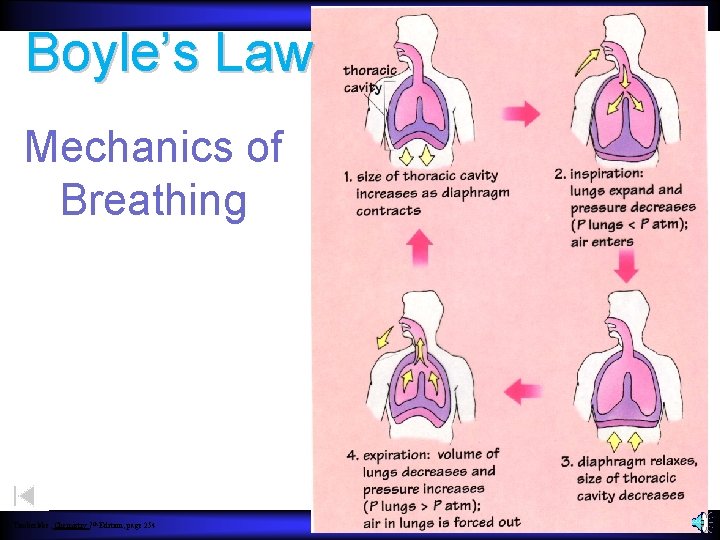
Boyle’s Law Mechanics of Breathing Timberlake, Chemistry 7 th Edition, page 254

Boyle’s Law Problem A balloon is filled with 30. L of helium gas at 1. 00 atm. What is the volume when the balloon rises to an altitude where the pressure is only 0. 25 atm? Given V 1 = 30 L P 1 = 1 atm P 2 =. 25 atm Unkown V 2 = ? L • Substitute and Solve V 2 0. 25 atm = 30 L x 1. 0 atm = 120 L Equation P 1 V 1 = P 2 V 2 T 1 T 2

Boyle’s Law Learning Check A gas occupies 100. m. L at 150. k. Pa. Find its volume at 200. k. Pa. Given V 1 = 100. m. L = 0. 100 L P 1 = 150. k. Pa P 2 = 200. k. Pa Unkown V 2 = ? L Equation P 1 V 1 = P 2 V 2 T 1 T 2 • Substitute and Solve V 2 x 200. k. Pa = 0. 100 L x 150. k. Pa= 75. 0 m. L 0. 0750 L

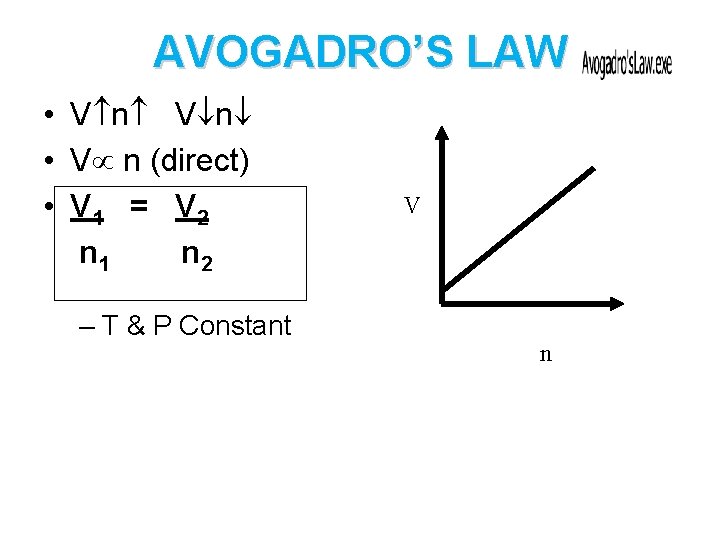
AVOGADRO’S LAW • V n (direct) • V 1 = V 2 n 1 n 2 – T & P Constant V n

Avogadro’s Law Problem A 3. 0 liter sample of gas contains 7. 0 moles. How much gas will there be, in order for the sample to be 2. 3 liters? P & T do not change Given V 1 = 3. 0 L n 1 = 7. 0 mol V 2 = 2. 3 L Unkown n 2 = ? mol • Substitute and Solve 3. 0 L = 2. 3 L = 7. 0 mol n 2 mol 5. 4 mol Equation P 1 V 1 = P 2 V 2 n 1 T 1 n 2 T 2

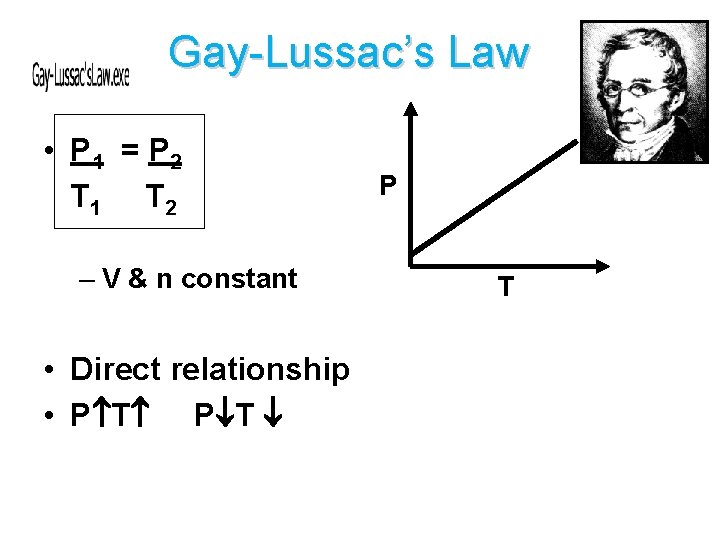
Gay-Lussac’s Law • P 1 = P 2 T 1 T 2 – V & n constant • Direct relationship • P T

Gay-Lussac Law • Collapsing Barrel

Gay-Lussac Law • Tank car implosion

COMBINED IDEAL GAS LAW • P 1 V 1 = P 2 V 2 n 1 T 1 n 2 T 2 • If P, V, n, or T are constant then they cancel out of the equation. • n usually constant (unless you add or remove gas), so • P 1 V 1 = P 2 V 2 T 1 T 2

Combined Gas Law Problem Ms. Evans travels to work in a hot air balloon from the Rocky Mountains. At her launch site, the temperature is 5. 00 °C, the atmospheric pressure is 0. 801 atm, and the volume of the air in the balloon is 120. 0 L. When she lands in Plano, the temperature is 28. 0 °C and the atmospheric pressure is 101. 3 k. Pa. What is the new volume of the air in the balloon? Given T 1 = 5. 0 o. C +273= 278 K P 1 = 0. 801 atm V 1 = 120. 0 L T 2 = 28. 0 o. C +273= 301 K P 2 = 101. 3 k. Pa = 1 atm Unkown V 2 = ? L Equation V 1 x P 1 = V 2 x P 2 T 1 T 2 Substitute and Solve V 2 x 1 atm = 120. 0 L x 0. 801 atm = 104 L 301 K 278 K

Combined Gas Law Learning Check Nitrogen gas is in a 7. 51 L container at 5. C and 0. 58 atm. What is the new volume of the gas at STP? Given T 1 = 5. 0 o. C +273= 278 K P 1 = 0. 58 atm V 1 = 7. 51 L T 2 = 273 K P 2 = 1 atm Unkown V 2 = ? L Equation V 1 x P 1 = V 2 x P 2 T 1 T 2 Substitute and Solve V 2 x 1. 0 atm = 7. 51 L x 0. 58 atm = 4. 3 L 273 K 278 K

Ideal Gas Law (“Pivnert”) PV=n. RT R = The Ideal Gas Constant R = 0. 0821 (L*atm) (mol*K) R = 8. 31 (L*k. Pa) (mol*K) • • • R = 62. 4 (L*mm Hg) (mol*K) V has to be in Liters, n in Moles, T in Kelvin, P can be in atm, k. Pa or mm. Hg * Choose which R to used based on the units of your pressure. P V (atm) (L) (k. Pa) (L) mm Hg (L) = n = (moles) R T (L*atm/mol*K) (L*k. Pa/mol*K) (L*mm. Hg/mol*K) (K)

Ideal Gas Law Problem A rigid steel cylinder with a volume of 20. 0 L is filled with nitrogen gas to a final pressure of 200. 0 atm at 27. 0 o. C. How many moles of gas does the cylinder hold? Given Unkown V = 20. 0 L moles of P = 200. 0 atm nitrogen? T =27. 0 o. C +273= 300 K Equation PV=n. RT R=. 0821 atm L/K Mole Substitute and Solve n 0821 atm L/K Mole x 300 K = 200. 0 atm x 20. 0 L= 162 moles

Ideal Gas Law Learning Check • A balloon contains 2. 00 mol of nitrogen at a pressure of 0. 980 atm and a temperature of 37 C. What is the volume of the balloon? Given Unkown n = 2. 00 mol V in L? P = 0. 980 atm T =37. 0 o. C +273= 310 K Equation PV=n. RT R=. 0821 atm L/K Mole Substitute and Solve 0. 980 atm x V= 2. 00 mol x. 0821 atm L/K Mole x 310 K = 51. 9 L

Dalton’s Law of Partial Pressure • The total pressure of a mixture of gases is equal to the sum of the partial pressures of the component gases. • Ptotal = Pgas 1 + Pgas 2 + P gas 3 + … A metal container holds a mixture of 2. 00 atm of nitrogen, 1. 50 atm of oxygen and 3. 00 atm of helium. What is the total pressure in the canister? 6. 5 atm

Welcome to Mole Island

Welcome to Mole Island

Welcome to Mole Island

Gas Stoichiometry Moles Liters of a Gas: – 2 C 4 H 10 (g) + 13 O 2(g) 8 CO 2(g) + 10 H 2 O(g) 2 mol + 13 mol 8 mol + 10 mol 2 L + 13 L 8 L + 10 L Recall: The coefficients in a chemical reaction represent molar amounts of substances taking part in the reaction. Avogadro’s principle states that one mole of any gas occupies 22. 4 L at STP. Thus when gases are involved, the coefficients in a balanced chemical equation represent not only molar amounts but also relatives volumes Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Stoichiometry Problem In the following combustion reaction, what volume of methane (CH 4) is needed to produce 26 L of water vapor? x L – CH 4 (g) + 2 O 2(g) 1 mol 1 L 26 L CO 2(g) + 2 H 2 O(g) 2 mol 2 L x L = 26 L x= 13 L 1 L 2 L

Gas Stoichiometry use ideal gas law PV=n. RT – Looking for grams or moles of gas? • Step 1: start with ideal gas law to find moles of gas • Step 2: 1 change to grams of gas Grams/mol? 1) Use Ideal Gas Law 2) Do stoichiometry calculations Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Example 1 How many grams of Al 2 O 3 are formed from 15. 0 L of O 2 at 97. 3 k. Pa & 21°C? PV=n. RT 4 Al(s) + 3 O 2(g) 2 Al 2 O 3(s) Given Unkown V O 2 = 15. 0 L O 2 grams of Al 2 O 3? R=. 0821 atm L/K Mole P O 2 = 97. 3 k. Pa= 0. 9605 atm Given liters: Start with T O 2 =21 o. C +273= 294 K Step 1: Calculate moles of O 2 Ideal Gas Law and calculate moles of O 2. n = PV = 0. 9605 atm x 15. 0 L = 0. 5969 mol O 2 RT 0. 0821 atm L/K Mole 294 K Step 2: Calculate mass of Al 2 O 3 Use stoich to convert moles of O 2 to grams Al 2 O 3. 0. 5969 mol O 2 = X mol Al 2 O 3 = 0. 3979 mol Al 2 O 3 3 mole. O 2 2 mole Al 2 O 3 0. 3979 mol Al 2 O 3 x 101. 96 g Al 2 O 3= 41 g Al 2 O 3 1 mol Al O Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Stoichiometry use ideal gas law • Looking for volume of gas? PV=n. RT • Step 1: start with stoichiometry conversion to find moles of gas • Step 2: use ideal gas law to find the volume Liters ? 1) Do stoichiometry calculations 2) Use Ideal Gas Law Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Example 2 What volume of CO 2 forms from 5. 25 g of Ca. CO 3 at 101. 3 k. Pa & 25ºC? Ca. CO 3 Ca. O + CO 2 Given Unkown PV=n. RT m = 5. 25 g Ca. CO 3 volume of CO 2? R=. 0821 atm L/K Mole P = 101. 3 k. Pa = 1 atm Looking for liters: Start with stoich T =25. 0 o. C +273= 298 K and calculate moles of CO 2. Step 1: Calculate moles of CO 2 5. 25 g Ca. CO 3 x 1 mole Ca. CO 3 = 0. 0525 mol Ca. CO 3 100 g Ca. CO 3 1 mole CO 2 = 1 mole Ca. CO 3 ; 0. 0525 mol CO 2 Plug this into the Ideal Gas Law to find volume. Step 2: Calculate volume of CO 2 V = n. RT = 0. 0525 mol CO 2 x. 0821 atm L/K Mole x 298 K = 1. 28 L P 1 atm