Gases Kinetic Molecular Theory The kinetic molecular theory



































- Slides: 38

Gases

Kinetic Molecular Theory The kinetic molecular theory is used to explain the behavior of gases. • All matter is made up of particles called atoms. • The atoms are in constant motion. • Collisions between the particles are elastic (no energy is gained or lost due to the collision).

Properties used to describe gases. The following four properties are used to describe gases: • Temperature (o. C or K)-how fast the particles making up the gas are moving. • Volume (L)-the amount of space the gas occupies (usually the size of the container) • Amount of sample (moles)-# of particles in the sample • Pressure (atm, k. Pa, mm Hg, torrs)

How is temperature measured? • Temperature is measured with a thermometer. • Almost all substances expand with an increase in temperature (exception is water). • Thermometers are designed so that the substances they contain (mercury, etc. ) expand contract more than the volume of the glass tube that contains them so that the column height of the substance changes.

Temperature Scales • Several temperature scales have been devised: - Fahrenheit (o. F): weather is measured using this scale. - Celsius (o. C): the scale used in the metric system. -Kelvin (K): based on absolute zero; used in the International System (SI).

Comparison of Temperature Scales

Comparison of Temperature Scales • Celsius degrees are larger in size than Fahrenheit degrees. • Celsius degrees are the same size as kelvins. • The Kelvin scale is the same as the Celsius scale (only 273 o higher). • The only temperature that is the same on the Celsius and Fahrenheit scale is -40 o.

Converting Between Scales • Celsius to Kelvin K = o. C + 273 • Kelvin to Celsius o. C = K - 273

Practice Problems • 65 o C = _______K • 25 o. C = _______K • -50 o. C = ______K • 300 K = _______o. C • 273 K = _______o. C • 150 K = _______o. C a) 338 K b) 298 K c) 223 K e) 0 o. C f) -123 o. C d) 27 o. C

Pressure • Pressure is the force that is exerted on a surface. • P = F/A • Units for pressure are N/m 2 • One pascal (Pa) = 1 N/m 2 • Since the pascal is a very small unit, the k. Pa is more commonly used. • 1 k. Pa = 1000 Pa

Practice Problem • A car tire makes contact with the ground on a rectangular area of. 12 m x. 18 m. If the car’s mass is 9300 N, what pressure does it exert on ground as it rests on all four tires?

Gases and Pressure • Gases exert pressure due to the collisions between the molecules and the walls of the container. • The atmosphere exerts a pressure of 14. 7 psi (pounds per square inch) • Gravity acts as the atmosphere’s container.

The atmosphere exerts a pressure that can support a column of mercury 760 mm tall. 1 atm of pressure = 760 mm Hg/torr = 14. 7 psi = 101. 3 k. Pa

Complete the following conversion problems: 1) 2) 3) 4) Convert 2. 2 atm to k. Pa. Convert 750 torrs to atm. Convert 202. 5 k. Pa to mm. Hg. Convert 10. 5 psi to atm.

The Components of the Atmosphere • The atmosphere consists of the following gases: Nitrogen (N 2) = 78% Oxygen (O 2) = 21 % Argon (Ar) = 0. 93% Carbon Dioxide (CO 2) = 0. 038%

The Structure of the Atmosphere • The atmosphere consists of five principal layers (starting closest to the earth and moving outward): 1) Troposphere (<20 km): where weather occurs, planes fly, etc. 2) Stratosphere (20 -50 km) : where ozone layer is located, weather balloons fly, etc. 3) Mesosphere (50 -85 km): where most meteors burn up 4) Thermosphere (85 -690 km): International Space Station located here, aurora borealis , etc. 5) Exosphere (690 -10, 000 km): mostly consists of hydrogen and helium

Layers of the atmosphere

Gas Laws

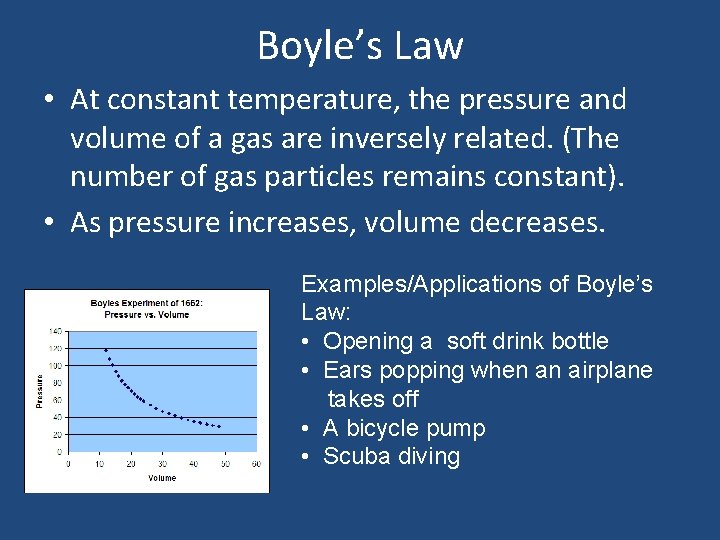
Boyle’s Law • At constant temperature, the pressure and volume of a gas are inversely related. (The number of gas particles remains constant). • As pressure increases, volume decreases. Examples/Applications of Boyle’s Law: • Opening a soft drink bottle • Ears popping when an airplane takes off • A bicycle pump • Scuba diving

Predicting Pressure and Volume Using Boyle’s Law • • • P 1 x V 1 = P 2 x V 2 P 1: Original/Starting Pressure V 1: Original/Starting Volume P 2: New/Resulting Pressure V 2: New/Resulting Volume

The volume of a gas at 99. 0 k. Pa is 300. 0 m. L. If the pressure is increased to 188 k. Pa, what will be the new volume? • • P 1 = 99. 0 k. Pa V 1 = 300. 0 m. L P 2 = 188 k. Pa V 2 = ? P 1 x V 1 = P 2 x V 2 (99. 0) (300. 0) = (188) x X = 158 m. L (The pressure increased, so the volume decreased).

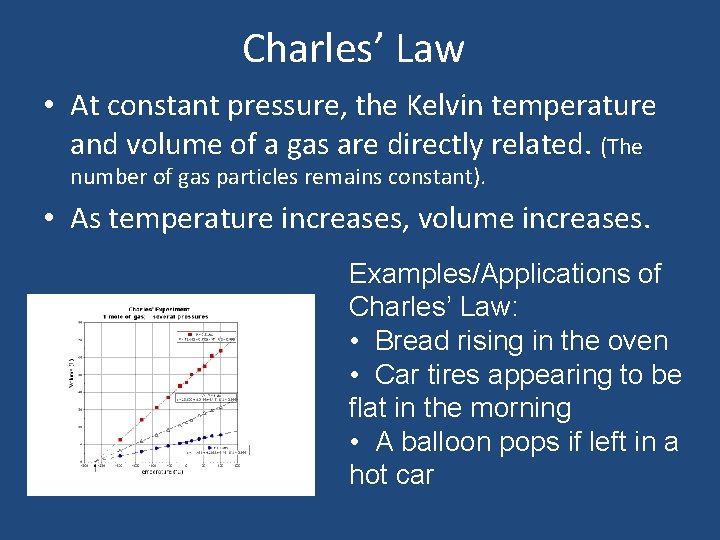
Charles’ Law • At constant pressure, the Kelvin temperature and volume of a gas are directly related. (The number of gas particles remains constant). • As temperature increases, volume increases. Examples/Applications of Charles’ Law: • Bread rising in the oven • Car tires appearing to be flat in the morning • A balloon pops if left in a hot car

Predicting Temperature and Volume Using Charles’ Law • V 1 = V 2 T 1 T 2 • • V 1: Original/Starting Volume T 1: Original/Starting Temperature (Kelvin) V 2: New/Resulting Volume T 2: New/Resulting Temperature (Kelvin)

A helium balloon in a closed car occupies a volume of 2. 32 L at 40. 0 o. C. If the car is parked on a hot day and the temperature inside rises to 75. 0 o. C, what is the new volume of the balloon (assuming the pressure remains constant)? • • V 1= 2. 32 L T 1 = 40. 0 o + 273 = 313 K T 2 = 75. 0 o + 273 = 348 K V 2 = ? V 1 = V 2 T 1 T 2 2. 32 = x 313 348 x = 2. 58 L (The temperature increased, so the volume increased also)

Gay-Lussac’s Law • At constant volume, the Kelvin temperature and pressure of a gas are directly related. (The number of gas particles remains constant). • As temperature increases, pressure increases. Everyday Examples/Applications of Gay-Lussac’s Law: • An aerosol can explodes if left in a fire. • A pressure cooker • http: //preparatorychemistry. com/Bishop_Gay_Lussac_frames. htm

Predicting Temperature and Pressure Using Gay-Lussac’s Law • P 1 = P 2 T 1 T 2 • • P 1: T 1 : P 2: T 2 : Original/Starting Pressure Original /Starting Temperature (in Kelvin) New/Resulting Pressure New/Resulting Temperature

A cylinder contain a gas which has a pressure of 125 k. Pa at a temperature of 200 K. Find the temperature of the gas which has a pressure of 100 k. Pa. P 1 = 125 k. Pa T 1 = 200 K P 2 = 100 k. Pa T 2 = ? P 1 = P 2 T 1 T 2 • 125 = 100 200 x • • • X=

Combined Gas Law • The combined gas law states the relationship among pressure, temperature, and volume of a fixed amount of gas. • All three variables have the same relationship to each other as they have in the other gas laws. • This law can be represented by the following equation: V 1 P 1 = V 2 P 2 T 1 T 2

Practice Problem • A sample of air in a syringe exerts a pressure of 1. 02 atm at 22. 0 o. C. The syringe is placed in a boiling water bath at 100. 0 o. C. The pressure is increased to 1. 23 atm by pushing the plunger in, which reduces the volume to 0. 224 m. L. What was the initial volume? • P 1 = 1. 02 atm P 1 V 1 = P 2 V 2 • T 1 = 22. 0 o. C + 273 = 295 K T 1 T 2 • V 1=? • P 2 = 1. 23 atm (1. 02)(x) = (1. 23)(0. 224) • T 2 = 100. 0 o. C + 273= 373. 0 K 295 373 • V 2 = 0. 224 m. L x = 0. 214 m. L

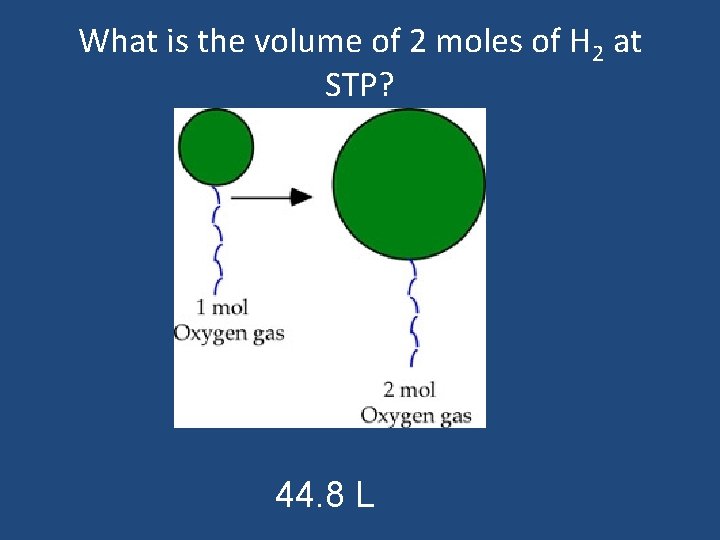
Avogadro’s Principle • Equal volumes of gases at the same temperature and pressure contain equal numbers of molecules. • 1 mole of any gas at standard temperature (0 o. C) and pressure (1 atm) occupies 22. 4 L of space. (STP) 22. 4 L is known as the molar volume.

What is the volume of 2 moles of H 2 at STP? 44. 8 L

Predicting Volume and Moles of Gases Using Avogadro’s Principle. • V 1 = V 2 n 1 n 2 • V 1 : Original/Starting Volume • n 1 : Original/Starting Number of Moles • V 2 : New/Resulting Volume • n 2: New/Resulting Number of Moles

What size container do you need to hold 0. 05 moles of N 2 gas at STP? V 1 = ? n 1 = 0. 05 moles V 2 = 22. 4 L n 2 = 1 mole V 1 = V 2 n 1 n 2 x = 22. 4. 05 1 X = 1. 12 L • •

Ideal Gas Law • The ideal gas law is a mathematical equation that describes the relationship among all 4 properties. • The formula works best when gases obey the assumptions of the kinetic molecular theory. • PV = n. RT • P is pressure; V is volume in liters; T is temperature in Kelvin; n is the number of moles; and R is the gas constant • R = 8. 314 if pressure is in k. PA; R= 0. 0821 if pressure is in atm; R= 62. 4 if pressure is in mm Hg or torrs.

Calculate the number of moles of ammonia gas contained in a 3. 0 L container at 300. 0 K with a pressure of 1. 50 atm. • V = 3. 0 L • P = 1. 50 atm • T = 300. 0 K • R = 0. 0821 • n=? • PV = n. RT (1. 50)(3. 0) = x (0. 0821)(300) X = 0. 18 mol

Graham’s Law • Diffusion is the term used to describe the movement of one material through another. • Effusion is a term used to describe the escape of a gas through an opening. • Example: Helium will effuse through a hole in a balloon. • Graham’s law states that the heavier the gas, the slower its rate of effusion.

Predicting Rates of Effusion Using Graham’s Law • Which gas will diffuse the fastest: – He or O 2 – H 2 or CO 2

Dalton’s Law of Partial Pressures • The total pressure of a mixture of gases is equal to the sum of the pressures of all of the gases in the mixture. • Ptotal = P 1 + P 2 + P 3 + … • A mixture of oxygen, nitrogen and hydrogen gases have a total pressure of 0. 97 atm. What is the partial pressure of oxygen if the partial pressure of nitrogen is 0. 70 atm and the partial pressure of hydrogen is 0. 12 atm? • 0. 97 = x + 0. 70 + 0. 12 • 0. 15 atm