Gas Law Calculations Bernoullis Principle Boyles Law Fast

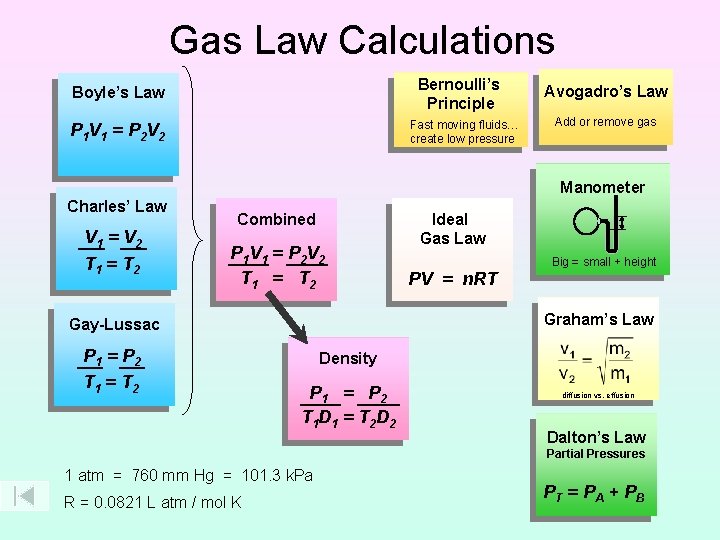
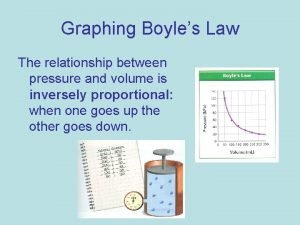
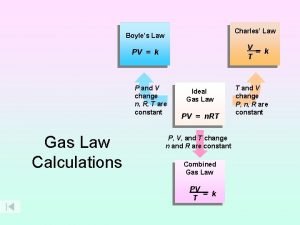
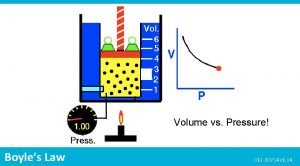
Gas Law Calculations Bernoulli’s Principle Boyle’s Law Fast moving fluids… create low pressure P 1 V 1 = P 2 V 2 Avogadro’s Law Add or remove gas Manometer Charles’ Law V 1 = V 2 T 1 = T 2 Combined P 1 V 1 = P 2 V 2 T 1 = T 2 PV = n. RT Big = small + height Graham’s Law Gay-Lussac P 1 = P 2 T 1 = T 2 Ideal Gas Law Density P 1 = P 2 T 1 D 1 = T 2 D 2 diffusion vs. effusion Dalton’s Law Partial Pressures 1 atm = 760 mm Hg = 101. 3 k. Pa R = 0. 0821 L atm / mol K PT = P A + P B

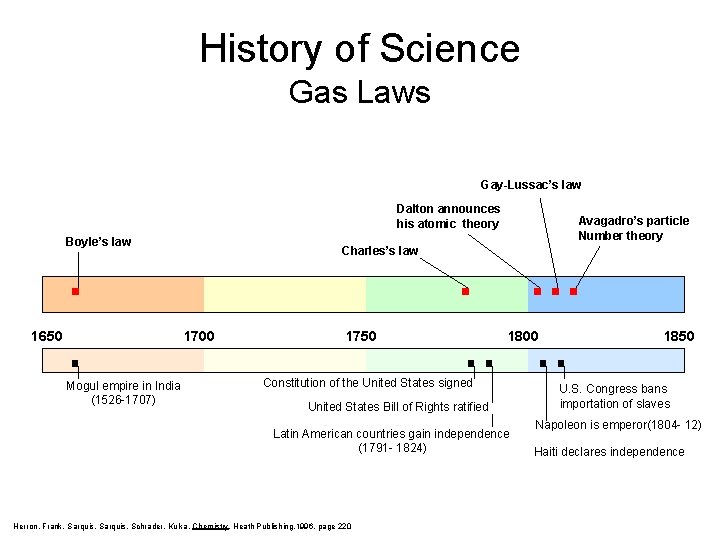
History of Science Gas Laws Gay-Lussac’s law Dalton announces his atomic theory Boyle’s law 1650 Charles’s law 1700 Mogul empire in India (1526 -1707) Avagadro’s particle Number theory 1750 1800 Constitution of the United States signed United States Bill of Rights ratified Latin American countries gain independence (1791 - 1824) Herron, Frank, Sarquis, Schrader, Kulka, Chemistry, Heath Publishing, 1996, page 220 1850 U. S. Congress bans importation of slaves Napoleon is emperor(1804 - 12) Haiti declares independence

Scientists • Evangelista Torricelli (1608 -1647) – Published first scientific explanation of a vacuum. – Invented mercury barometer. • Robert Boyle (1627 - 1691) – Volume inversely related to pressure (temperature remains constant) • Jacques Charles (1746 -1823) – Volume directly related to temperature (pressure remains constant) • Joseph Gay-Lussac (1778 -1850) – Pressure directly related to temperature (volume remains constant)

Apply the Gas Law • The pressure shown on a tire gauge doubles as twice the volume of air is added at the same temperature. Avogadro’s principle • A balloon over the mouth of a bottle containing air begins to inflate as it stands in the sunlight. Charles’ law • An automobile piston compresses gases. • • An inflated raft gets softer when some of the gas is allowed to escape. Avogadro’s principle A balloon placed in the freezer decreases in size. Charles’ law • A hot air balloon takes off when burners heat the air under its open end. • When you squeeze an inflated balloon, it seems to push back harder. Boyle’s law • A tank of helium gas will fill hundreds of balloons. Boyle’s law • Model: When red, blue, and white ping-pong balls are shaken in a box, the effect is the same as if an equal number of red balls were in the box. Dalton’s law Boyle’s law Charles’ law

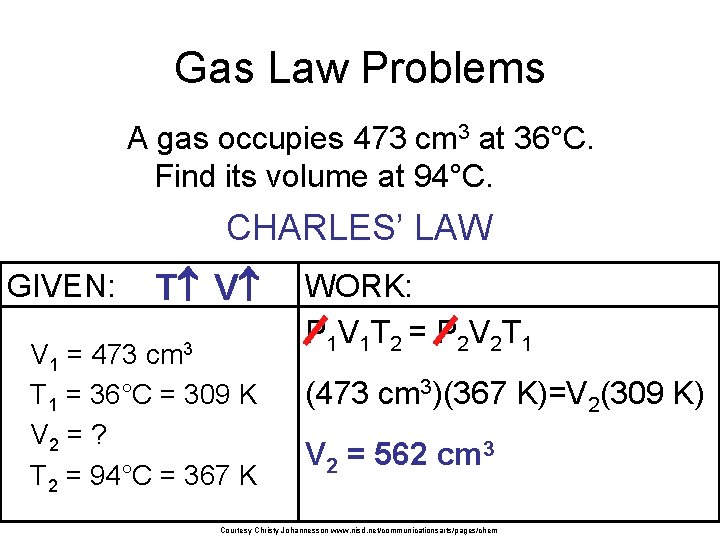
Gas Law Problems A gas occupies 473 cm 3 at 36°C. Find its volume at 94°C. CHARLES’ LAW GIVEN: T V V 1 = 473 cm 3 T 1 = 36°C = 309 K V 2 = ? T 2 = 94°C = 367 K WORK: P 1 V 1 T 2 = P 2 V 2 T 1 (473 cm 3)(367 K)=V 2(309 K) V 2 = 562 cm 3 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Law Problems A gas occupies 100. m. L at 150. k. Pa. Find its volume at 200. k. Pa. BOYLE’S LAW GIVEN: P V WORK: P 1 V 1 T 2 = P 2 V 2 T 1 V 1 = 100. m. L P 1 = 150. k. Pa V 2 = ? P 2 = 200. k. Pa (150. k. Pa)(100. m. L)=(200. k. Pa)V 2 = 75. 0 m. L Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Law Problems A gas occupies 7. 84 cm 3 at 71. 8 k. Pa & 25°C. Find its volume at STP. COMBINED GAS LAW GIVEN: P T V WORK: P 1 V 1 T 2 = P 2 V 2 T 1 V 1 = 7. 84 cm 3 P 1 = 71. 8 k. Pa T 1 = 25°C = 298 K V 2 = ? P 2 = 101. 325 k. Pa T 2 = 273 K (71. 8 k. Pa)(7. 84 cm 3)(273 K) =(101. 325 k. Pa) V 2 (298 K) V 2 = 5. 09 cm 3 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Law Problems A gas’ pressure is 765 torr at 23°C. At what temperature will the pressure be 560. torr? GAY-LUSSAC’S LAW GIVEN: P T P 1 = 765 torr T 1 = 23°C = 296 K P 2 = 560. torr T 2 = ? WORK: P 1 V 1 T 2 = P 2 V 2 T 1 (765 torr)T 2 = (560. torr)(309 K) T 2 = 226 K = -47°C Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

The Combined Gas Law (This “gas law” comes from “combining” Boyle’s, Charles’, and Gay-Lussac’s law) P = pressure (any unit will work) V = volume (any unit will work) T = temperature (must be in Kelvin) 1 = initial conditions 2 = final conditions

A gas has volume of 4. 2 L at 110 k. Pa. If temperature is constant, find pressure of gas when the volume changes to 11. 3 L. P 1 V 1 T 1 = P 2 V 2 T 2 P 1 V 1 = P 2 V 2 110 k. Pa (4. 2 L) = P 2 (11. 3 L) P 2 = 40. 9 k. Pa (temperature is constant) (substitute into equation)

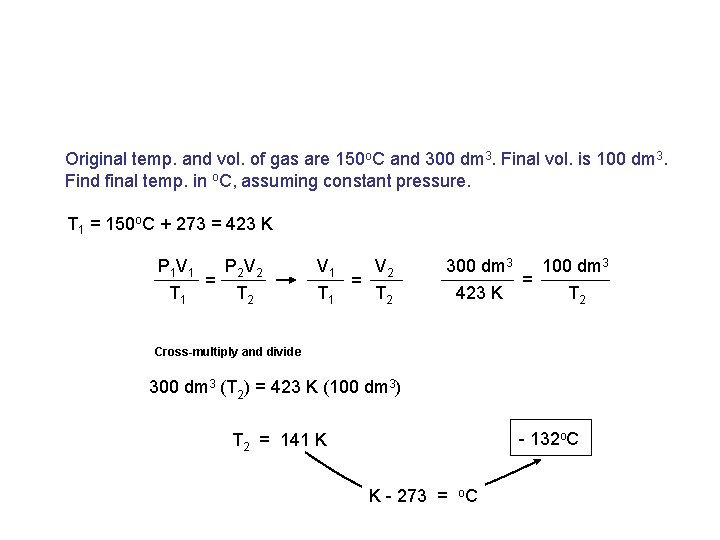
Original temp. and vol. of gas are 150 o. C and 300 dm 3. Final vol. is 100 dm 3. Find final temp. in o. C, assuming constant pressure. T 1 = 150 o. C + 273 = 423 K P 1 V 1 T 1 = P 2 V 2 V 1 T 2 T 1 = V 2 300 dm 3 T 2 423 K = 100 dm 3 T 2 Cross-multiply and divide 300 dm 3 (T 2) = 423 K (100 dm 3) - 132 o. C T 2 = 141 K K - 273 = o. C

A sample of methane occupies 126 cm 3 at -75 o. C and 985 mm Hg. Find its volume at STP. T 1 = -75 o. C + 273 = 198 K P 1 V 1 T 1 = P 2 V 2 985 mm Hg (126 cm 3) T 2 198 K = 760 mm Hg (V 2) 273 K Cross-multiply and divide: 985 (126) (273) = 198 (760) V 2 = 225 cm 3

Density of Gases Density formula for any substance: For a sample of gas, mass is constant, but pres. and/or temp. changes cause gas’s vol. to change. Thus, its density will change, too. ORIG. VOL. If V (due to P NEW VOL. or T ), then… D Density of Gases Equation: ORIG. VOL. If V (due to P NEW VOL. or T ), then… D ** As always, T’s must be in K.

Density of Gases Density formula for any substance: For a sample of gas, mass is constant, but pres. and/or temp. changes cause gas’s vol. to change. Thus, its density will change, too. Because mass is constant, any value can be put into the equation: lets use 1 g for mass. For gas #1: Take reciprocal of both sides: Substitute into equation “new” values for V 1 and V 2 For gas #2:

A sample of gas has density 0. 0021 g/cm 3 at – 18 o. C and 812 mm Hg. Find density at 113 o. C and 548 mm Hg. T 1 = – 18 o. C + 273 = 255 K P 1 P 2 = T 1 D 1 T 2 D 2 T 2 = 113 o. C + 273 = 386 K 812 mm Hg 548 mm Hg = 255 K (0. 0021 g/cm 3) 386 K (D 2) Cross multiply and divide (drop units) 812 (386)(D 2) = 255 (0. 0021)(548) D 2 = 9. 4 x 10– 4 g/cm 3

A gas has density 0. 87 g/L at 30 o. C and 131. 2 k. Pa. Find density at STP. T 1 = 30 o. C + 273 = 303 K P 1 P 2 = T 1 D 1 T 2 D 2 131. 2 k. Pa = 303 K (0. 87 g/L) 101. 3 k. Pa 273 K (D 2) Cross multiply and divide (drop units) 131. 2 (273)(D 2) = 303 (0. 87)(101. 3) D 2 = 0. 75 g/L

Find density of argon at STP. m 39. 9 g D = = V 22. 4 L 1. 78 g/L 1 mole of Ar = 39. 9 g Ar = 6. 02 x 1023 atoms Ar = 22. 4 L @ STP

Find density of nitrogen dioxide at 75 o. C and 0. 805 atm. D of NO 2 @ STP… T 2 = 75 o. C + 273 = 348 K 1 (348) (D 2) = 273 (2. 05) (0. 805) D 2 = 1. 29 g/L

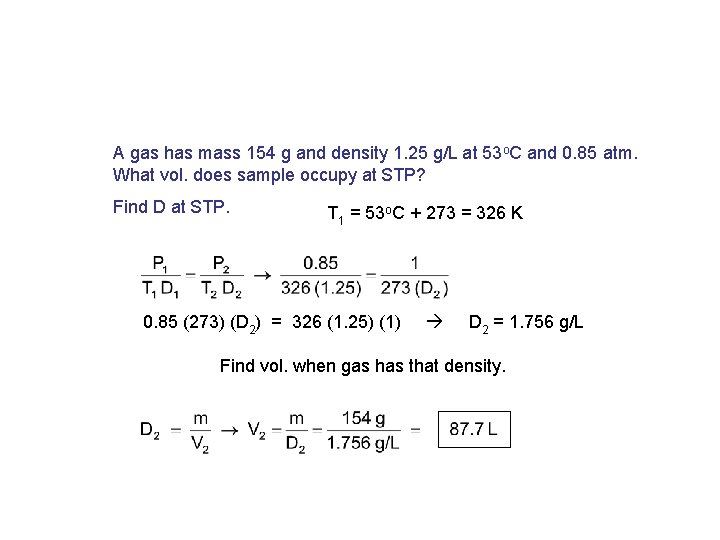
A gas has mass 154 g and density 1. 25 g/L at 53 o. C and 0. 85 atm. What vol. does sample occupy at STP? Find D at STP. T 1 = 53 o. C + 273 = 326 K 0. 85 (273) (D 2) = 326 (1. 25) (1) D 2 = 1. 756 g/L Find vol. when gas has that density.

Density and the Ideal Gas Law Combining the formula for density with the Ideal Gas law, substituting and rearranging algebraically: M = Molar Mass P = Pressure R = Gas Constant T = Temperature in Kelvin