Chapter 13 Gases 13 1 The Gas Laws

























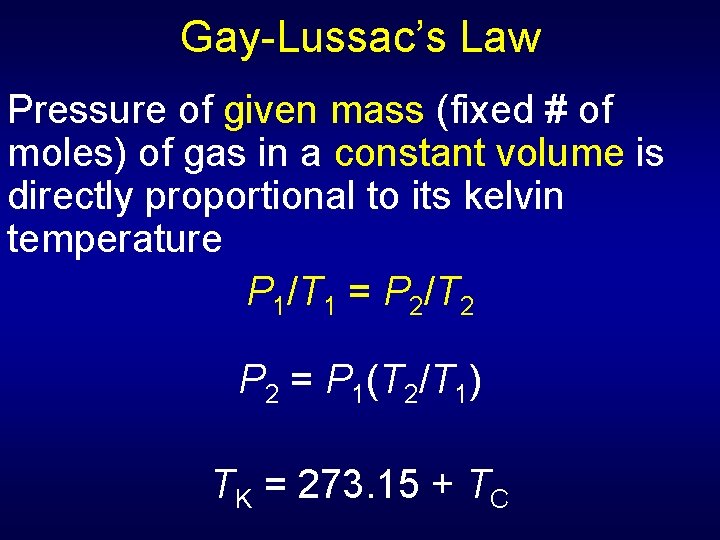






























- Slides: 65

Chapter 13 – Gases 13. 1 The Gas Laws 13. 2 The Ideal Gas Law (Part I – Equation Only) 13. 3 Gas Stoichiometry

Section 13. 2 The Ideal Gas Law The ideal gas law relates the number of particles to pressure, temperature, and volume. • Relate the amount of gas present to its pressure, temperature, and volume using the ideal gas law.

Section 13. 2 The Ideal Gas Law Key Concept • The ideal gas law relates the amount of a gas present to its pressure, temperature, and volume PV = n. RT

Gas Laws – Mechanistic and Empirical “Named” laws described in section 13. 1 were empirically determined from experiments – stated relationships “fit the data” Example: Boyle experimentally determined that P & V are inversely related but there was no underlying understanding of why this occurs – this is an empirical model

Gas Laws – Mechanistic and Empirical Ideal gas law is mechanistic – it can be derived by using the basic theory (kineticmolecular) of how gases behave; the underlying mechanism that leads to the equation is known and understood Ideal gas law was formulated after the empirical (named) laws were discovered It predicted the same behavior as the empirical laws but provided a way to understand why they were true

Kinetic-Molecular Theory (KMT) of Gases (see section 12. 1) Mostly empty space No attractions/repulsions between particles Constant straight-line motion until collisions with other particles or walls Collisions perfectly elastic: KE constant • T constant, KE constant All gases have same KEavg at a given T

Ideal Gas Law Relationship between pressure P, volume V, Kelvin temperature T, and number of moles n PV = n. RT T must be expressed in units of kelvin Equation derived using KMT assumptions R = Gas Constant – value depends upon units used for P

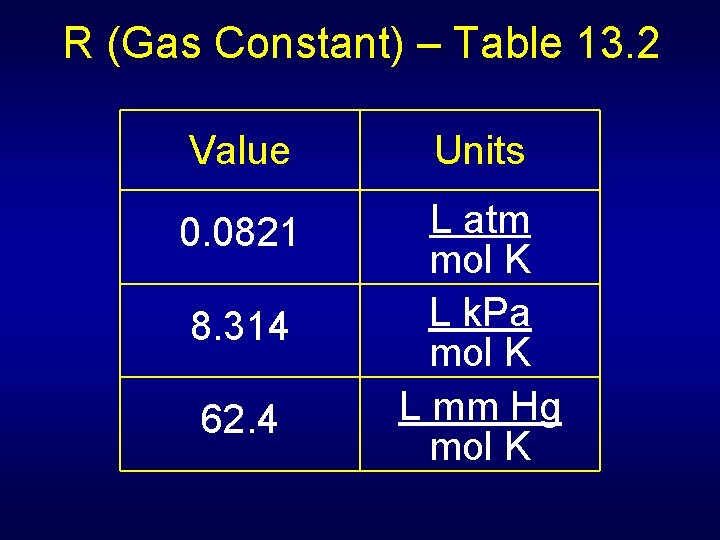
R (Gas Constant) – Table 13. 2 Value Units 0. 0821 L atm mol K L k. Pa mol K L mm Hg mol K 8. 314 62. 4

Ideal Gas Law – Dependence on n PV = n. RT Fixed V, T then P n Fixed P, T V n

Ideal Gas Law: Example Problem 13. 6 Calculate number of moles of NH 3 for V = 3. 0 L, T = 3. 00 x 102 K, P = 1. 50 atm PV = n. RT n = PV / RT n = (1. 50 atm 3. 0 L) / (8. 21 x 10 -2 L atm/mol K 3. 00 x 102 K) n = 0. 18 mol Note that value of R was chosen that has atm as the pressure unit

Practice (Ideal Gas Law) Problems 26 – 30, page 455 Problems 68, 69, 74, 75, 77 – 78, pages 468 – 9 Problems 15, 16, 18, page 985

Ideal Gas Law and the Combined Gas Law PV = n. RT If the # of moles of gas (n) is fixed, then PV/T = n. R = constant If P, V, T conditions change (from 1 to 2) P 1 V 1/T 1 = P 2 V 2/T 2 (have derived the Combined Gas Law)

Combined & Named Gas Laws (Subject of Section 13. 1) For given mass (fixed # moles) of gas P 1 V 1/T 1 = P 2 V 2/T 2 3 laws can be derived from this: Fix T: P 1 V 1 = P 2 V 2 (Boyle’s) Fix P: V 1/T 1 = V 2/T 2 (Charles’) Fix V: P 1/T 1 = P 2/T 2 (Gay-Lussac’s)

Chapter 13 – Gases 13. 1 The Gas Laws 13. 2 The Ideal Gas Law (Part I) 13. 3 Gas Stoichiometry

Section 13. 1 The Gas Laws For a fixed amount of gas, a change in one variable—pressure, temperature, or volume—affects the other two. • State the relationships among pressure, temperature, and volume of a constant amount of gas. • Apply the gas laws to problems involving the pressure, temperature, and volume of a constant amount of gas.

Section 13. 1 The Gas Laws Key Concepts • Boyle’s law states that the volume of a fixed amount of gas is inversely proportional to its pressure at constant temperature. P 1 V 1 = P 2 V 2 • Charles’s law states that the volume of a fixed amount of gas is directly proportional to its kelvin temperature at constant pressure.

Section 13. 1 The Gas Laws Key Concepts • Gay-Lussac’s law states that the pressure of a fixed amount of gas is directly proportional to its kelvin temperature at constant volume. • The combined gas law relates pressure, temperature, and volume in a single statement.

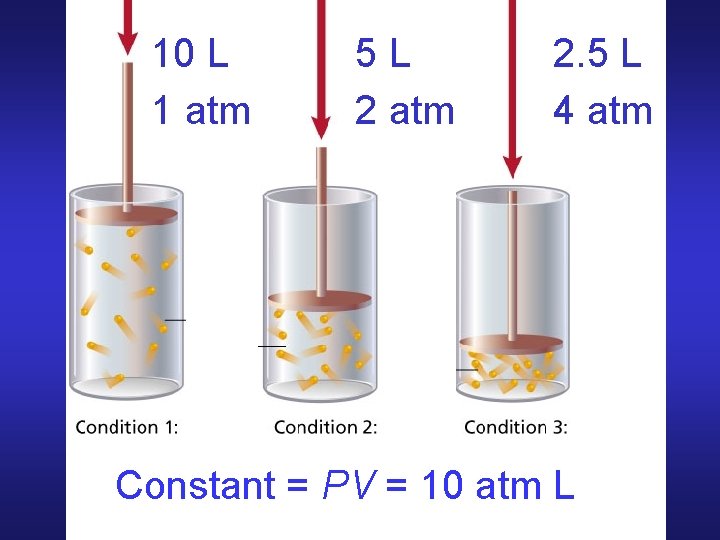
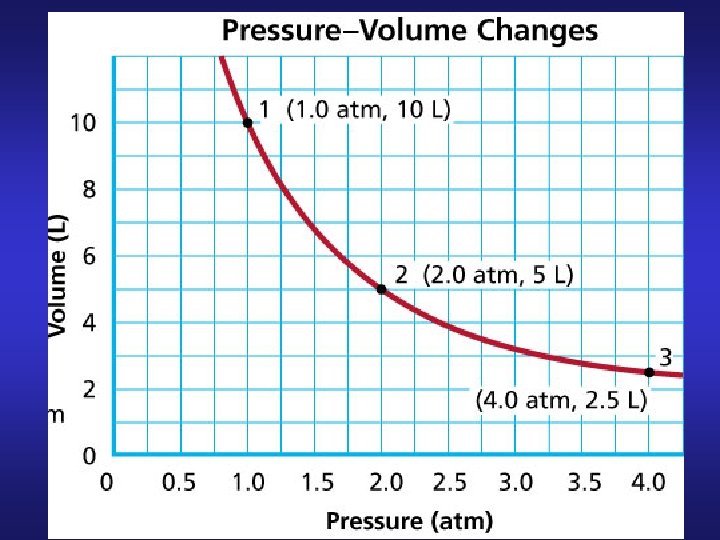
Boyle’s Law Volume of given mass (fixed # of moles) of gas held at constant T varies inversely with pressure P 1 V 1 = P 2 V 2 PV = constant V 2 = V 1 (P 1/P 2)

10 L 1 atm 5 L 2 atm 2. 5 L 4 atm Constant = PV = 10 atm L


Boyle’s Law – Example Problem 13. 1 Diver blows bubble of volume = 0. 75 L at 10 m depth & pressure = 2. 25 atm. Volume of bubble at surface when pressure = 1. 03 atm? P 1 V 1 = P 2 V 2 = V 1 (P 1/P 2) V 2 = 0. 75 L (2. 25 atm / 1. 03 atm) V 2 = 1. 6 L

Practice (Boyle’s Law) Problems 1 - 3 page 443 Problems 59 – 60, page 468 Problems 1 – 2, page 984

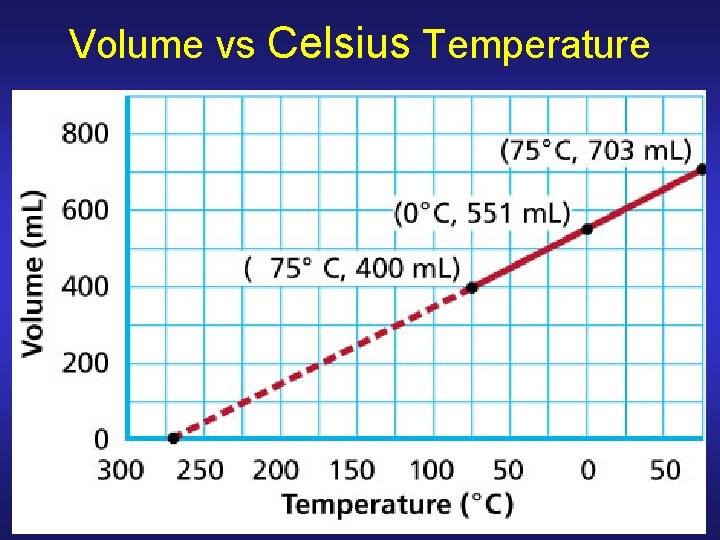
Charles’s Law Volume of given mass (fixed # of moles) of gas held at constant P is directly proportional to its kelvin temperature V 1/T 1 = V 2/T 2 V 2 = V 1(T 2/T 1) TK = 273. 15 + TC

V change with T at fixed P

Volume vs Celsius Temperature

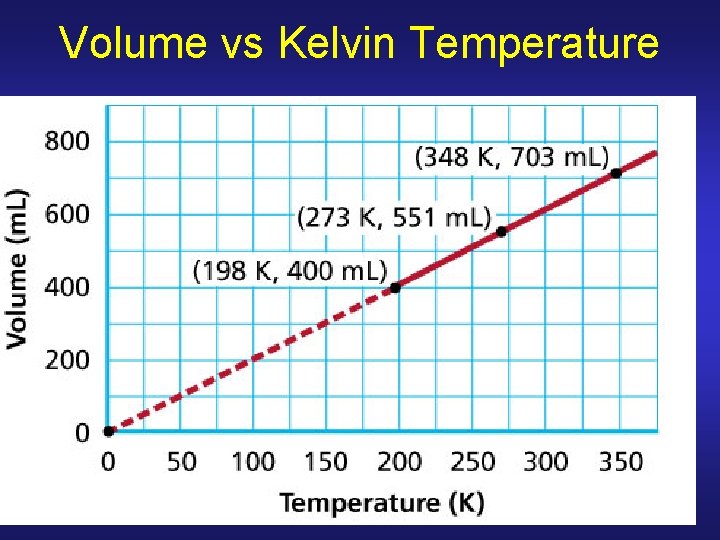
Volume vs Kelvin Temperature

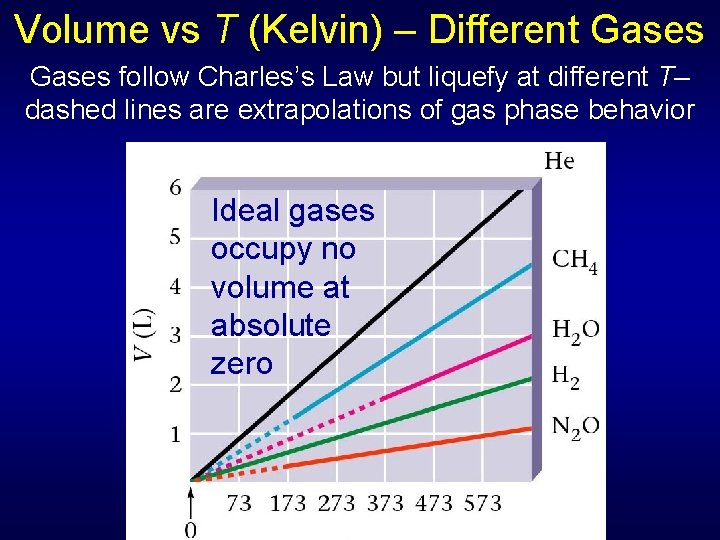
Volume vs T (Kelvin) – Different Gases follow Charles’s Law but liquefy at different T– dashed lines are extrapolations of gas phase behavior Ideal gases occupy no volume at absolute zero

Charles’s Law: Example Problem 13. 2 Balloon has volume of 2. 32 L at 40. 0 C. Volume at 75. 0 C if P remains constant? V 1/T 1 = V 2/T 2 T 1 = 40. 0 C + 273. 15 = 313. 2 K T 2 = 75. 0 C + 273. 15 = 348. 2 K V 2 = V 1 (T 2/T 1) V 2 = 2. 32 L (348. 2 K/ 313. 2 K) V 2 = 2. 58 L

Practice (Charles’s Law) Problems 4 – 7, page 446 Problems 55, 58, 59 page 448 Problems 3 – 4, page 984

Joseph Louis Gay-Lussac (1778 – 1850) http: //en. wikipedia. org/wiki/Gay-Lussac French chemist & physicist. Known mostly for 2 laws related to gases, & for his work on alcohol-water mixtures, which led to the degrees Gay-Lussac used to measure alcoholic beverages in many countries. Prof. of physics at Sorbonne (1808 to 1832), a post which he only resigned for the chair of chemistry at the Jardin des Plantes. In 1802, first formulated law stating that if mass and pressure of gas are held constant, then gas volume increases linearly as temperature rises.

Gay-Lussac’s Law P change with T at fixed V
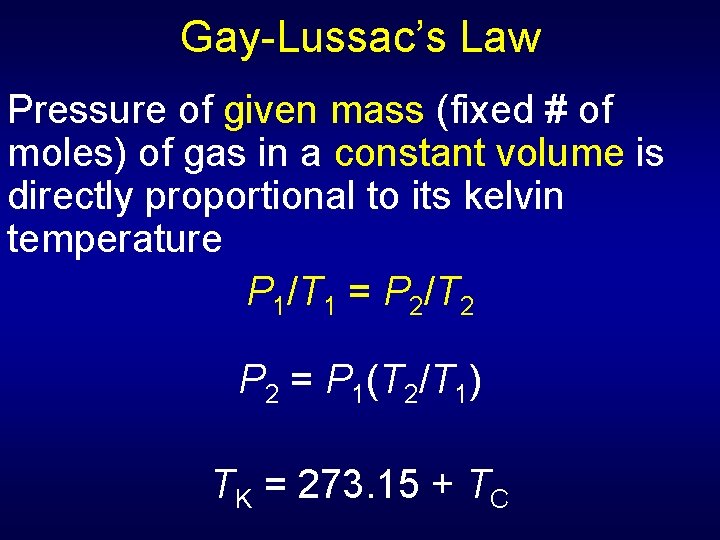
Gay-Lussac’s Law Pressure of given mass (fixed # of moles) of gas in a constant volume is directly proportional to its kelvin temperature P 1/T 1 = P 2/T 2 P 2 = P 1(T 2/T 1) TK = 273. 15 + TC

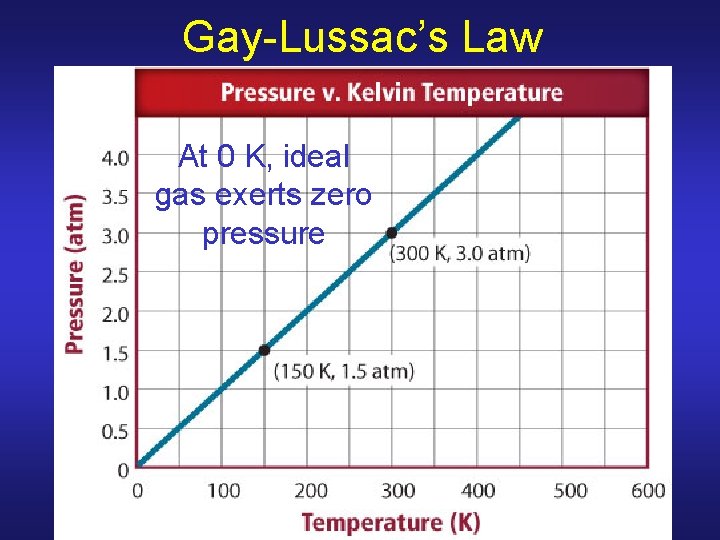
Gay-Lussac’s Law At 0 K, ideal gas exerts zero pressure

Gay-Lussac’s Law: Example Problem 13. 3 Pressure of O 2 in canister is 5. 00 atm at 25. 0 C. New pressure at T of -10. 0 C? P 1/T 1 = P 2/T 2 T 1 = 25. 0 C + 273. 15 = 298. 2 K T 2 = -10. 0 C + 273. 15 = 263. 2 K P 2 = P 1(T 2/T 1) P 2 = 5. 00 atm (263. 2 K / 298. 2 K) P 2 = 4. 41 atm

Practice (Gay-Lussac’s Law) Problems 8 – 10, page 448 Problem 18, page 451 Problem 59 page 468 Problems 5 – 7, page 984

Combined Gas Law If P, V, T conditions change (from 1 to 2) P 1 V 1/T 1 = P 2 V 2/T 2

Combined Gas Law: Practice Problem 13. 4 Gas at 110 k. Pa and 30. 0 C fills flexible container with initial V of 2. 00 L. If T and P raised to 80. 0 C and 440 k. Pa, new V? T 1 = 30. 0 C + 273. 15 = 303. 2 K T 2 = 80. 0 C + 273. 15 = 353. 2 K P 1 V 1/T 1 = P 2 V 2/T 2 V 2 = V 1 (P 2 /P 1) (T 1/T 2) V 2 = 2. 00 L (440 k. Pa/ 110 k. Pa) (303. 2 K/ 353. 2 K) V 2 = 0. 58 L

Practice (Combined Gas Law) Problems 11 – 13, page 450 Problem 60 page 468 Problems 8 – 9, page 984

Gas Laws Summary – Table 13. 1 All require fixed n (moles of gas)

Chapter 13 – Gases 13. 1 The Gas Laws (includes Combined) 13. 2 The Ideal Gas Law (Part II Avogadro’s Principle, Gas Density, Real Gases) 13. 3 Gas Stoichiometry

Section 13. 2 The Ideal Gas Law The ideal gas law relates the number of particles to pressure, temperature, and volume. • Relate number of particles and volume using Avogadro’s principle. • Compare the properties of real and ideal gases.

Section 13. 2 The Ideal Gas Law Key Concepts • Avogadro’s principle states that equal volumes of gases at the same pressure and temperature contain equal numbers of particles. • The ideal gas law can be used to find molar mass if the mass of the gas is known, or the density of the gas if its molar mass is known. • At very high pressures and very low temperatures, real gases behave differently than ideal gases.

Avogadro’s Principle Equal volumes of gases at same T and P contain equal numbers of particles Size of gas particles negligible compared to volume occupied, so it doesn’t matter which gas you are using

Molar Volume of Gas Volume occupied by one mole of gas at 0. 00 C and 1. 00 atmosphere pressure T, P conditions known as STP – Standard Temperature and Pressure At STP, 1 mole of any gas occupies 22. 4 L Key to lots of problems involving gases at STP

Molar Volume of Gas: Example Problem 13. 5 V of 2. 00 kg of methane at STP? 2. 00 kg CH 4 1. 00 x 103 g/kg mol CH 4/16. 05 g CH 4 = 125 mol CH 4 22. 4 L CH 4 / mol CH 4 (at STP) V = 2. 80 x 103 L

Practice (Avogadro’s Principle & Molar Volume) Problems 20 – 25, page 453 Problems 67, 71, 73 pages 468 -9 Problems 10 - 14, page 984

Ideal Gas Law: Calculate M or Density PV = n. RT n = # moles = mass /molar mass = m / M PV = m. RT / M MP = m. RT / V M = m. RT / PV M = (m/V) RT / P (m/V) = density = D M = D RT / P or D = MP / RT For a given P, T , if know: 1. mass m & V, can compute molar mass M 2. density D, can compute molar mass M 3. molar mass M, can compute density D

Practice (Molar Mass, Density from Ideal Gas Law) Problems 70, 72, 76 page 469 Problems 17 – 18, page 985

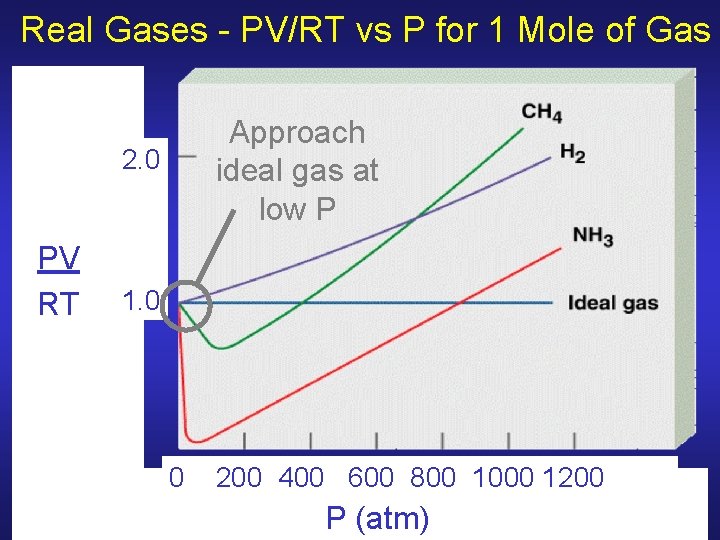
Ideal Gas Law - Deviations No gas truly ideal, but most behave as ideal gases over wide range of T & P Deviations happen at high P and low T where assumptions of KMT break down • Volume of gas no longer negligible • An ideal gas can’t be liquefied • Intermolecular forces more significant ² Polar molecules especially affected

Ideal Gas Law - Deviations Polar molecules have larger attractive forces between particles and generally do not behave as ideal gases at low T where slower-moving particles can be affected by these forces Large gas particles occupy more space and deviate more from ideal gases at high density (high P, low T) where there is less empty space

Real Gases - PV/RT vs P for 1 Mole of Gas Approach ideal gas at low P 2. 0 PV RT 1. 0 0 200 400 600 800 1000 1200 P (atm)

Chapter 13 – Gases 13. 1 The Gas Laws 13. 2 The Ideal Gas Law 13. 3 Gas Stoichiometry

Section 13. 3 Gas Stoichiometry When gases react, the coefficients in the balanced chemical equation represent both molar amounts and relative volumes. • Determine volume ratios for gaseous reactants and products by using coefficients from chemical equations. • Apply gas laws to calculate amounts of gaseous reactants and products in a chemical reaction.

Section 13. 3 Gas Stoichiometry Key Concepts • The coefficients in a balanced chemical equation specify volume ratios for gaseous reactants and products. • The gas laws can be used along with balanced chemical equations to calculate the amount of a gaseous reactant or product in a reaction.

Balanced Equation & Gas Volumes Gas laws can be applied to calculate stoichiometry of reactions in which gases are reactants or products 2 H 2(g) + O 2(g) → 2 H 2 O(g) 2 mol H 2 reacts with 1 mol O 2 to produce 2 mol water vapor Coefficients in balanced equation represent volume ratios for gases if P and T are fixed during reaction

Balanced Equation & Gas Volumes CH 4(g) + 2 O 2(g) CO 2(g) + 2 H 2 O(g) There is a one-to-one relationship between number of moles and gas volume

Balanced Equation & Gas Volumes 2 C 4 H 10(g) + 13 O 2(g) 8 CO 2(g) + 10 H 2 O(g) Interpreted as moles: 2 mol butane + 13 mol oxygen 8 mol carbon dioxide + 10 mol water Avogadro’s principle can also be volume 2 L butane + 13 L oxygen 8 L carbon dioxide + 10 L water

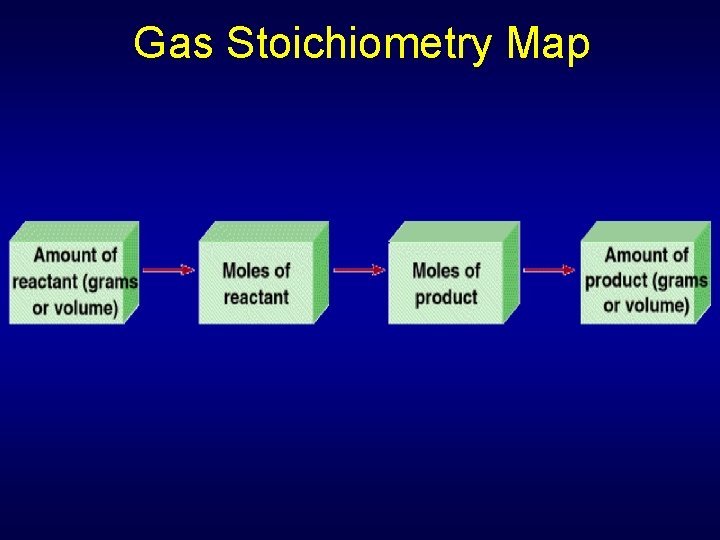
Gas Stoichiometry Map

Practice – Gas Stoichiometry How many mol of hydrogen gas are required to react with 1. 50 mol oxygen gas in the following reaction? 2 H 2(g) + O 2(g) → 2 H 2 O(g) A. B. C. D. 1. 00 2. 00 3. 00 4. 00 ?

V to. V Stoichiometry: Practice Problem 13. 7 Volume of oxygen gas needed for complete combustion of 4. 00 L of propane (C 3 H 8) assuming P and T remain constant? C 3 H 8(g) + 5 O 2(g) 3 CO 2(g) + 4 H 2 O(g) 4. 00 L C 3 H 8 5 L O 2 / L C 3 H 8 = 20. 0 L O 2

Practice – Gas Stoich. (all V to V) Problems 38 – 41, page 461 Problems 84 – 86, page 469 Problems 19 – 20, page 985

Combo Mass/Volume Problems Need: a) Balanced equation b) At least one mass or V for product or reactant c) Conditions under which volumes measured

Combo Mass/Volume – Prob 13. 8 N 2(g) + 3 H 2(g) 2 NH 3(g) 5. 00 L N 2 reacts completely P = 3. 00 atm T = 298 K Mass of ammonia produced? 5. 00 L N 2 [2 L NH 3/1 L N 2] = 10. 0 L NH 3 volume ratio from equation

Combo Mass/Volume – Prob 13. 8 N 2(g) + 3 H 2(g) 2 NH 3(g) 10. 0 L NH 3 P = 3. 00 atm T = 298 K n = PV/RT = ( 3. 00 atm 10. 0 L ) (298 K 0. 0821 L atm/mol K) = 1. 23 mol NH 3 Molar mass NH 3 = 17. 04 g/mol 1. 23 mol NH 3 17. 04 g NH 3/mol NH 3 = 21. 0 g NH 3

Practice (Stoich. m & V combo) Problems 42 – 45, page 463 Problems 88 – 90, page 469 Problems 21 – 22, page 985