Controllo delle operazioni nelle linee A Agnetis MODELLI

Controllo delle operazioni nelle linee * **A. Agnetis: ”MODELLI COMBINATORI NELLA PRODUZIONE FLESSIBILE”, Dispense ad uso esclusivo degli studenti, disponibili nella cartella 08_09 AU 9 crediti, nella pagina web: http: //nicolo. dia. uniroma 3. it/ Altri riferimenti * R. G. Askin, C. R. Stantridge: “Modeling and Analysis of manufacturing system”, John Wiley & Sons. 1993 * S. French: “SEQUENCING AND SCHEDULING, An Introduction to the Mathematics of the Job-Shop”, Ellis Horwood. 1982

min Cm S Nelle precedenti unità didattiche abbiamo risolto il problema per: - n lavori di 2 operazioni strettamente sequenziate, ciascuna delle quali ha bisogno di una macchina di una linea senza buffer intermedi -2 lavori di m operazioni strettamente sequenziate, ciascuna delle quali ha bisogno di una macchina di una linea con buffer intermedi (qui sotto raffigurata per m = 4) Il problema non è risolvibile con algoritmi semplici per n lavori ed m macchine, con o senza buffer M 1 B M 2 B M 3 B Linea di 4 macchine con buffer M 4

Prima di affrontare esempi “facili” di linee con buffer, consideriamo un’altra semplice applicazione: minimizzare il tempo di ciclo Cm di n lavori da eseguire ripetitivamente con mix 11… 111 (n volte): si può applicare Gilmore e Gomery, attribuendo ad ogni lavoro Ji stato di inizio ai e stato di fine bi Ji-1 Ji ai sulla macchina M 1 M 2 M 1 bi sulla su M 2 NO BUFFER Quando finisce l’ultimo lavoro del ciclo su M 1, vi entra il primo Nel grafo dei lavori non si aggiunge il lavoro “riposo” J 0. Infatti la linea non riposa “mai” e alla fine della sequenza di ciclo M 2 opera sull’ultimo lavoro Ji(n) mentre M 1 opera sul primo Ji(1) 1 2 n i

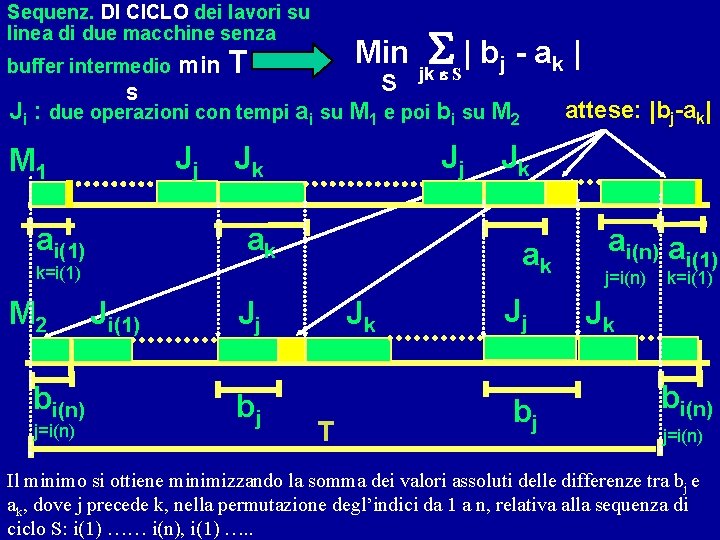
Sequenz. DI CICLO dei lavori su linea di due macchine senza buffer intermedio Min min T S S | b j - ak | jk e S attese: |bj-ak| Ji : due operazioni con tempi ai su M 1 e poi bi su M 2 Jj M 1 ai(1) Jj Jk ak ak k=i(1) M 2 bi(n) j=i(n) Ji(1) Jj bj Jk Jk T Jj bj ai(n) ai(1) j=i(n) k=i(1) Jk bi(n) j=i(n) Il minimo si ottiene minimizzando la somma dei valori assoluti delle differenze tra bj e ak, dove j precede k, nella permutazione degl’indici da 1 a n, relativa alla sequenza di ciclo S: i(1) …… i(n), i(1) …. .

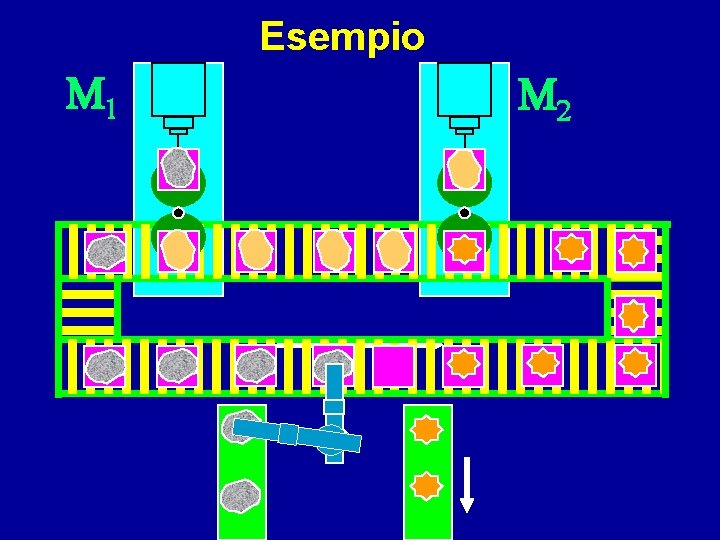
Esempio M 1 M 2

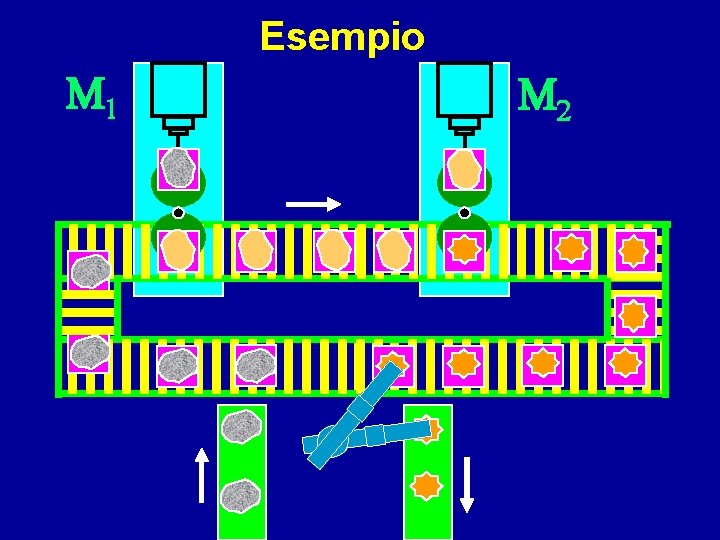
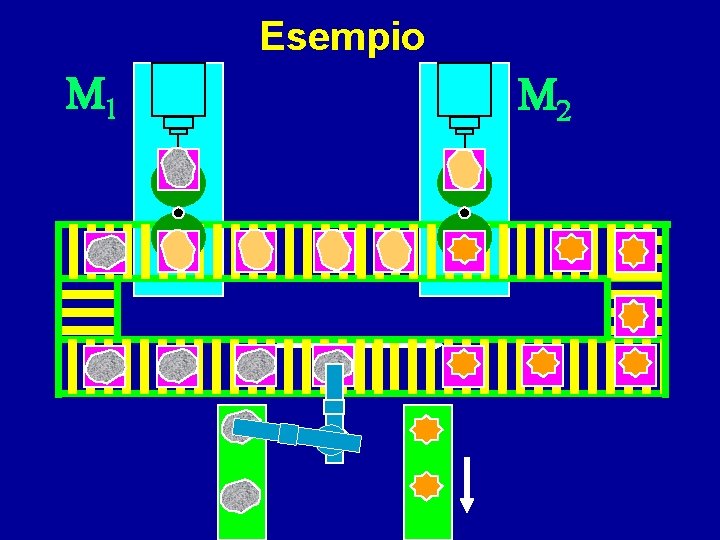
Il sistema rappresenta una linea di produzione in cui i pezzi sono lavorati in serie da 2 macchine Un pezzo, dopo la lavorazione, torna alla stazione di carico e scarico Tra le due macchine c’è un buffer con 4 posti

Esempio M 1 M 2

Esempio M 1 M 2

Flow shop In una linea esiste un vincolo tecnologico detto “flow shop”: tutti i lavori devono visitare le macchine nello stesso ordine Il Flow shop è un caso particolare di Job Shop Quando non altrimenti specificato, si intende che i lavori possono aspettare tra un’operazione e la seguente (ATTENZIONE: grazie ai buffer, le macchine possono operarli in ordine diverso)

Permutation schedule Quando in un flow shop si ha uno schedule nel quale le macchine processano i lavori nello stesso ordine (cioè quando: se la macchina M 1 processa Ji prima Jk, ciò è vero anche per le altre macchine), allora si ha un “Permutation schedule” ATTENZIONE. Senza buffer si ha sempre un Permutation schedule

INDICI REGOLARI Cm è un particolare, importante, “indice regolare” cioè una funzione non decrescente dei tempi di completamento dei lavori: f (C 1…Cn) Quando l’indice di comportamento è regolare, in un Flow Shop, senza perdita di generalità, ci si può limitare a considerare un “Permutation flow shop” sulle prime due macchine

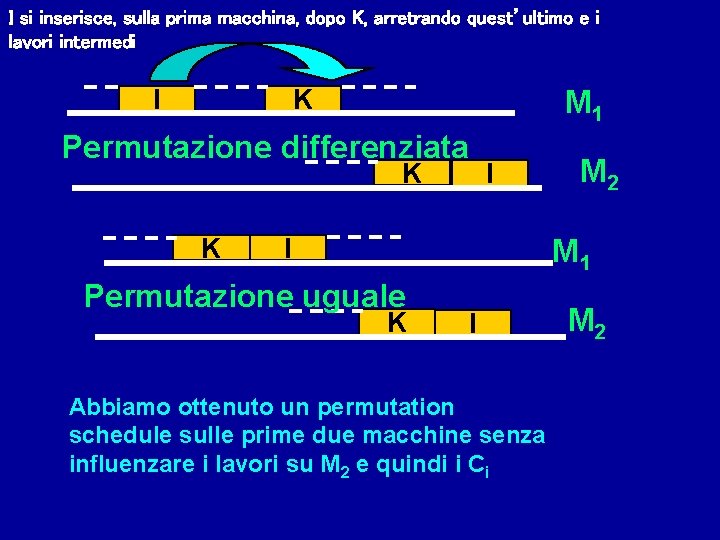
I si inserisce, sulla prima macchina, dopo K, arretrando quest’ultimo e i lavori intermedi I K M 1 Permutazione differenziata K K I I M 2 M 1 Permutazione uguale K I Abbiamo ottenuto un permutation schedule sulle prime due macchine senza influenzare i lavori su M 2 e quindi i Ci M 2

Indice di comportamento Cm Quando l’indice è Cm, in un Flow Shop ci si può limitare a considerare un “Permutation flow shop” sulle ultime due macchine , senza perdita di generalità

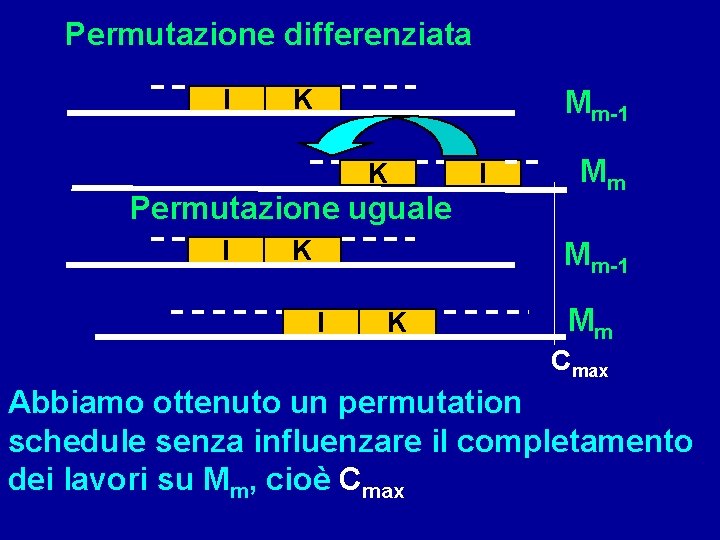
Permutazione differenziata I K Mm-1 K Permutazione uguale I K I Mm Mm-1 I K Mm Cmax Abbiamo ottenuto un permutation schedule senza influenzare il completamento dei lavori su Mm, cioè Cmax

PROBLEMA n LAVORI 2 MACCHINE Min { Fmax (= Cm)} Si usa indicare questo problema con (n /2/F/Fmax): il primo campo indica il numero dei lavori, il secondo il numero di risorse, il terzo la corrispondenza tra operazioni e risorse utilizzate, il terzo l’indice di comportamento

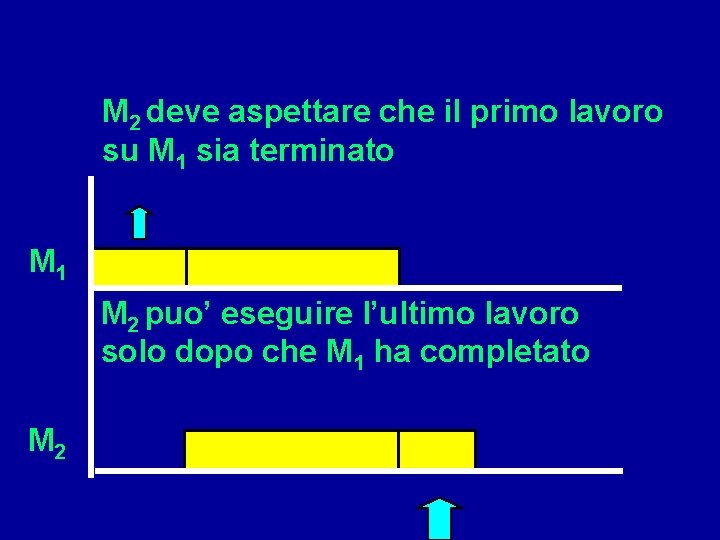
M 2 deve aspettare che il primo lavoro su M 1 sia terminato M 1 M 2 puo’ eseguire l’ultimo lavoro solo dopo che M 1 ha completato M 2

ALGORITMO DI JOHNSON ai = pi 1 tempo di processamento di Ji su M 1 bi = pi 2 tempo di processamento di Ji su M 2

ALGORITMO DI JOHNSON Se 1) ak = min{ a 1, . . , an, b 1, …bn} uno schedule ottimo nel quale Jk è processato per primo. 2) bu = min{ a 1, . . , an, b 1, …bn} uno schedule ottimo nel quale Ju è processato per ultimo.

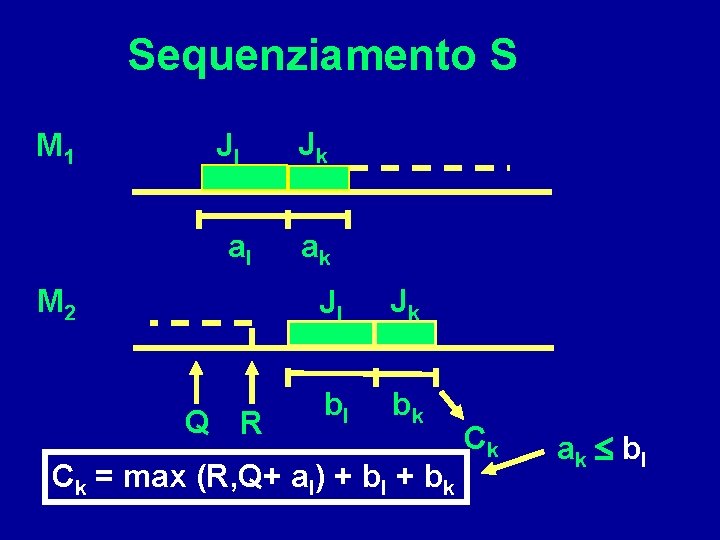
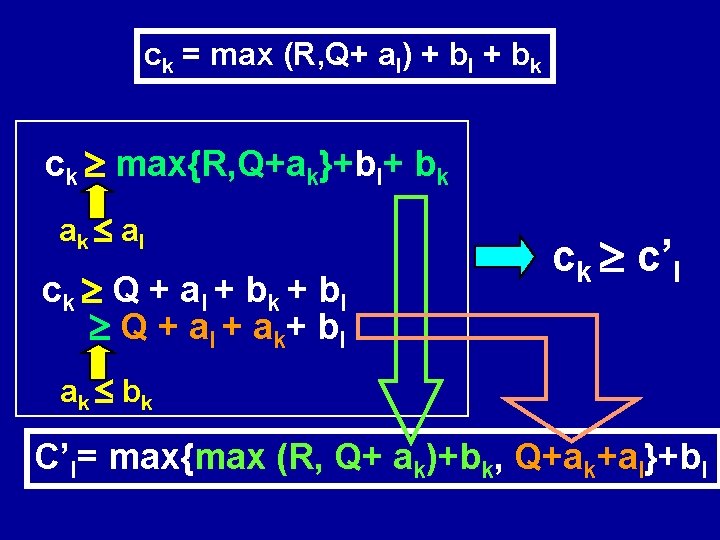
Sequenziamento S M 1 Jl al M 2 Q R Jk ak Jl Jk bl bk Ck = max (R, Q+ al) + bl + bk Ck ak b l

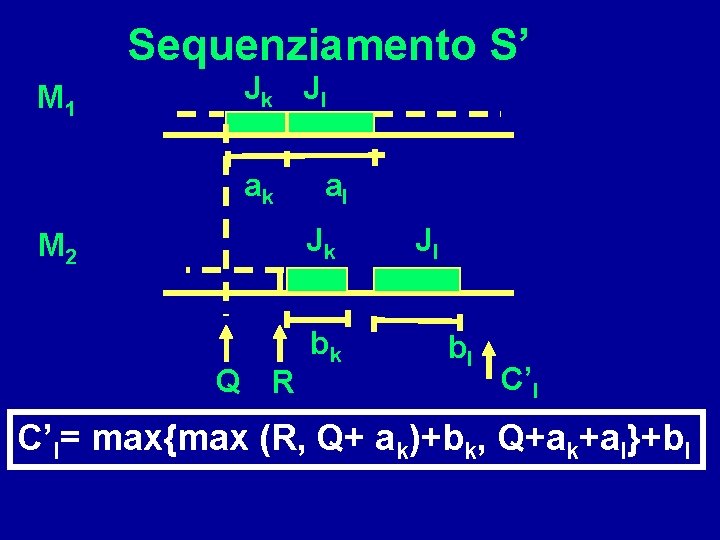
Sequenziamento S’ M 1 Jk Jl ak al Jk M 2 Q R bk Jl bl C’l= max{max (R, Q+ ak)+bk, Q+ak+al}+bl

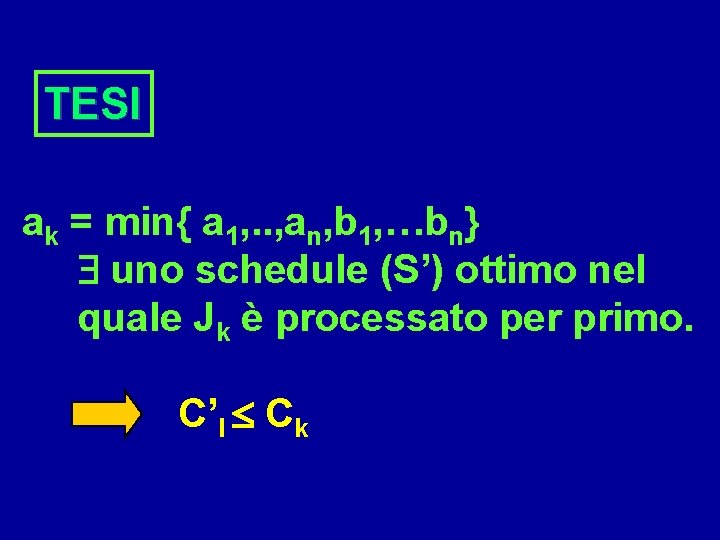
TESI ak = min{ a 1, . . , an, b 1, …bn} uno schedule (S’) ottimo nel quale Jk è processato per primo. C’l Ck

ck = max (R, Q+ al) + bl + bk ck max{R, Q+ak}+bl+ bk ak a l ck Q + a l + b k + b l Q + a l + a k+ b l ck c’l ak b k C’l= max{max (R, Q+ ak)+bk, Q+ak+al}+bl

ALGORITMO Si è dimostrato che si può anticipare Jk rispetto al Jl che lo precede in una schedule ottima senza alcuna ipotesi sulla schedule dei lavori sequenziati prima di Jl. Ne consegue che, assegnato Jk al primo posto, lo stesso ragionamento si applica agli n-1 lavori ancora da schedulare. Da cui l’algoritmo che segue

Algoritmo di Johnson (1954) Passo 1 K = 1, l = n Passo 2 NS : = { J 1, … Jn} Passo 3 Se aj = min (ai , bi )) i : Ji N S i(k) = j NS : = NS/ {Jj} k: = k+1

Algoritmo di Johnson (1954) Passo 4 Se bj = min (ai , bi )) i : Ji N S i(l) = j NS : = NS/ {Jj} l: = l-1 Passo 5 Se NS { } Passo 3 Altrimenti la sequenza ottima è {Ji(. )}

Esercizio su Johnson I tempi sulle macchine sono: Lavori: 1 su M 1 1 su M 2 6 2 2 6 3 3 6 4 4 5 5 5 3 6 7 5 Per vedere quanto si guadagna con il buffer, si minimizzi rispetto alla sequenza Cm quando non c’è buffer intermedio (con Gilmore e Gomery)

Esercizio su Johnson I tempi sulle macchine sono: Lavori: 1 su M 1 1 su M 2 6 2 2 6 3 3 6 4 4 5 Johnson 5 5 3 6 7 5 La sequenza ottima, di Johnson, è: 1 -2 -3 -4 -6 -5 Dal Gantt si vede che: Cm= ai(1) + i=1, . . n bi =32 cioè, dopo la prima, non ci sono attese in M 2, così come non ci sono in M 1 per la presenza del buffer intermedio Se inoltre, come accade con questa sequenza di Johnson, ai(k) bi(k-1) per k=2, …, n, allora eliminando il buffer intermedio Cm non aumenta, anche se si possono creare attese di M 1

Sequenziamento generale* su due macchine (n /2/G*/Fmax) Tipo A Lavori solo su M 1 Tipo B Lavori solo su M 2 Tipo C prima su M 1 poi su M 2 Tipo D prima su M 2 poi su M 1 *senza rivisitazione della stessa macchina

Sequenziamento generale su due macchine (n /2/G*/ Fmax) SA qualsiasi sequenza dei lavori di tipo A SB qualsiasi sequenza dei lavori di tipo B

SC SD sequenza di Johnson di quelli di tipo C sequenza di Johnson di quelli di tipo D Le sequenze ottime sono allora: su M 1 Sc SA Sd su M 2 Sd SB SC

Sequenziamento con tre macchine

Sequenziamento per flusso su tre macchine M 1 M 2 M 3 Con tempi di processamento qualsiasi è un problema difficile. Se min pi 1 max pi 2 i=1, …, n il problema è facile.

M 1 ai = pi 1 + pi 2 bi = pi 2 + pi 3 M 2 M 3 Algoritmo di Johnson Sequenza ottima si devono considerare solo le permutazioni (stesso sequenziamento sulle tre macchine)

Linea monoprodotto con assiemature (modello: pettine): lotto, flusso Minimo tempo di completamento: pezzo singolo, lotto finito, linea satura

Sistemi di movimentazione PIPELINE In questo tipo di sistemi : pipeline/ linee seriali/ flow shop i pezzi sono trasportati da un sistema di movimentazione unidirezionale. I pezzi possono muoversi solo dalla macchina Mj alla Mj+1

IPOTESI DI LAVORO Ogni macchina può eseguire un qualunque insieme di operazioni; tutte le macchine impiegano lo stesso tempo per eseguire una stessa operazione.

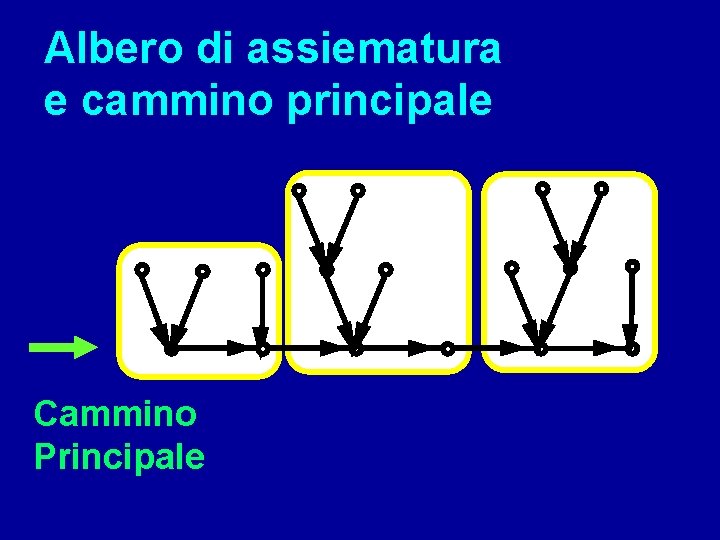
Albero di assiematura e cammino principale Cammino Principale

Esiste un cammino principale di operazioni strettamente ordinate, ciascuna delle quali deve essere preceduta da un albero di operazioni secondarie di predisposizione per quella principale corrispondente La definizione di principale per un’operazione è relativa all’assegnazione ad una macchina, nel senso che le secondarie devono essere assegnate alla stessa macchina che esegue la corrispondente principale

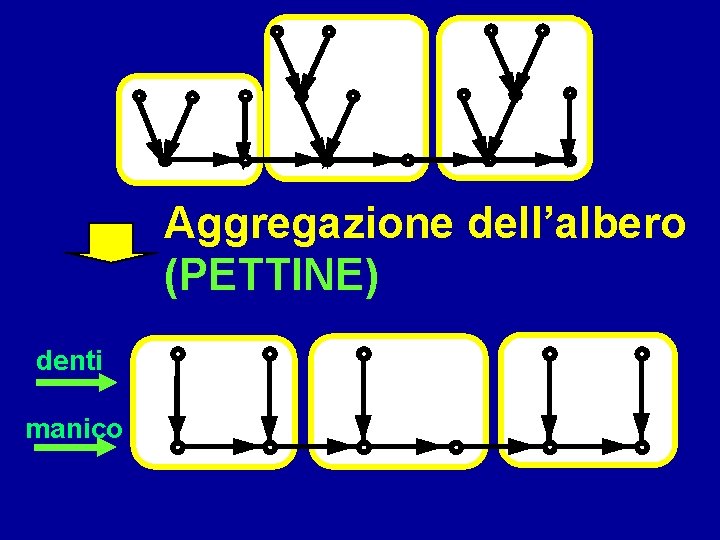
Aggregazione dell’albero (PETTINE) denti manico

IPOTESI DI LAVORO Il sistema deve produrre un numero totale di q unità identiche Il prodotto è caratterizzato da un albero di assiematura, avente la struttura di pettine

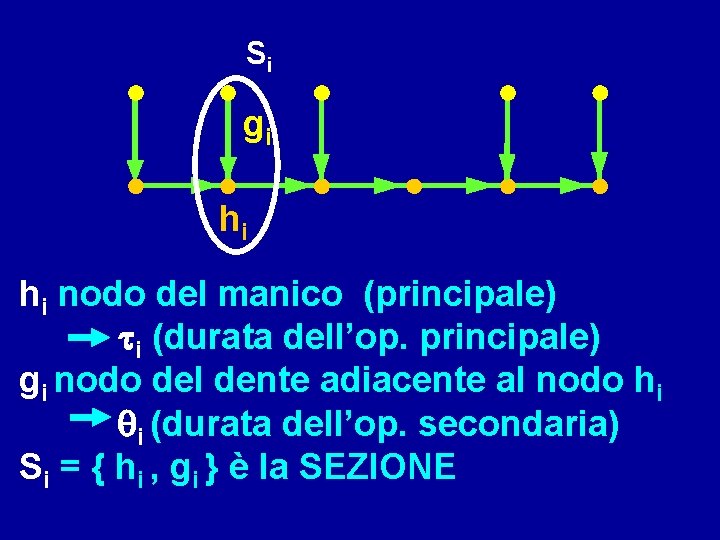
Si gi hi hi nodo del manico (principale) ti (durata dell’op. principale) gi nodo del dente adiacente al nodo hi qi (durata dell’op. secondaria) Si = { hi , gi } è la SEZIONE

Per ipotesi ogni operazione secondaria (e. g. : di predisposizione) è assegnata alla stessa macchina che esegue la corrispondente operazione principale (e. g. : di assiematura) CIOE’ se un nodo gi è assegnato ad una macchina, anche il corrispondente nodo del manico hi deve essere assegnato alla stessa macchina

L’assegnamento di operazioni alle macchine che si vuole determinare è unico per tutti i pezzi dello stesso tipo L’assegnamento è unico e definisce una PARTIZIONE dell’albero. Si vuol trovare l’assegnamento che minimizza il tempo di completamento dei q pezzi uguali

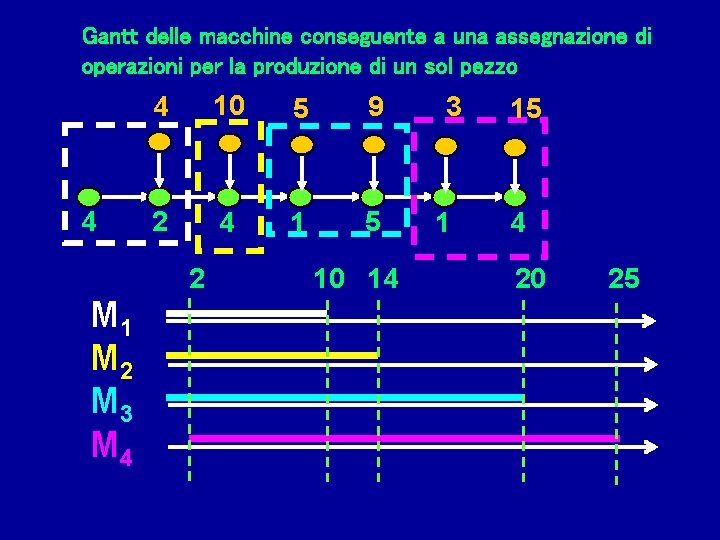
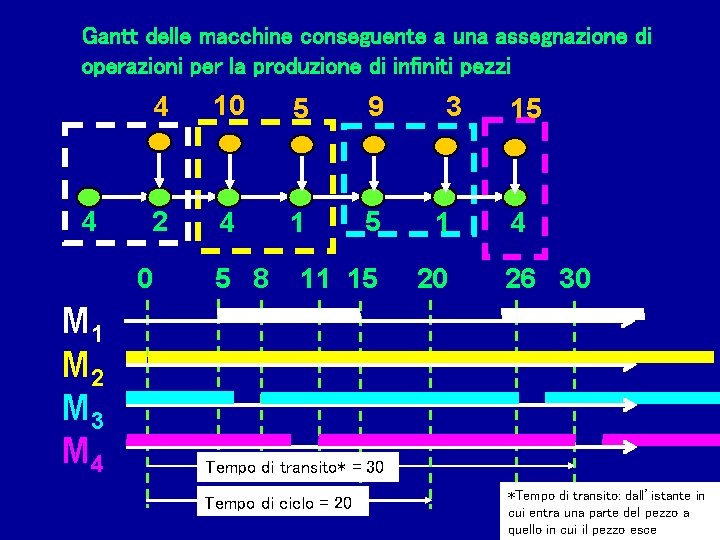
Gantt delle macchine conseguente a una assegnazione di operazioni per la produzione di un sol pezzo 4 4 10 5 9 2 4 1 5 2 M 1 M 2 M 3 M 4 10 14 3 1 15 4 20 25

L’assegnamento di operazioni a m macchine produce una m_partizione P {P 1, P 2, …, Pm} delle sezioni del pettine le operazioni nella classe Pj sono assegnate alla macchina Mj Per ipotesi la partizione riguarda le sezioni del pettine: i se hi Pk gi Pk

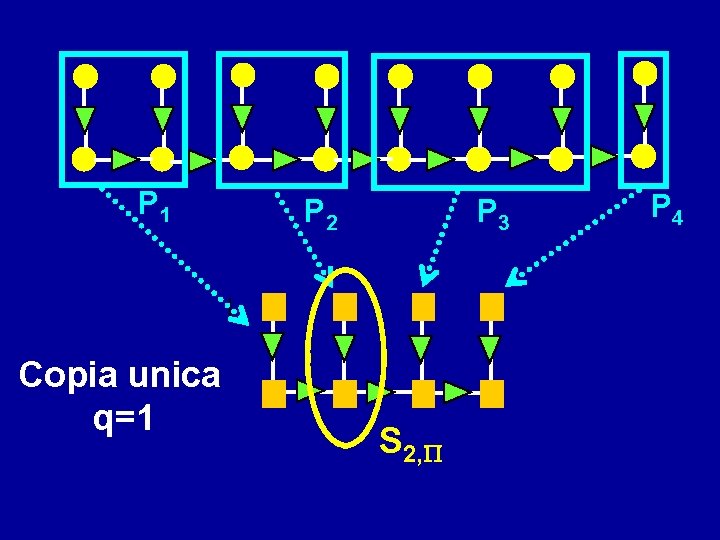
Data una partizione ammissibile P {P 1 , . , Pm} di un pettine C , associamo a C e P un nuovo pettine CP avente m sezioni vj è il j-esimo nodo del manico di CP uj è il suo dente la sezione Sj, P di CP corrisponde alla classe Pj di P tj, P è il peso di vi (somma dei pesi degli hj) qj, P è il peso di ui (somma dei pesi dei gj)

P 1 Copia unica q=1 P 2 P 3 S 2, P P 4

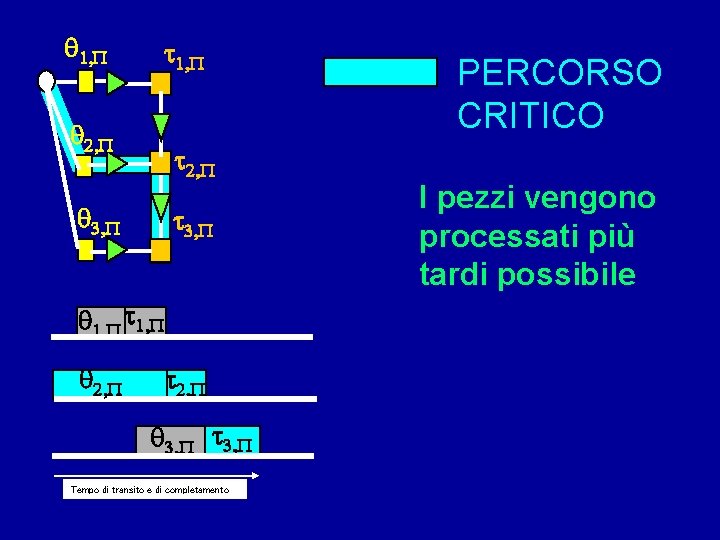
q 1, P t 1, P q 2, P t 2, P q 3, P t 3, P Tempo di transito e di completamento PERCORSO CRITICO I pezzi vengono processati più tardi possibile

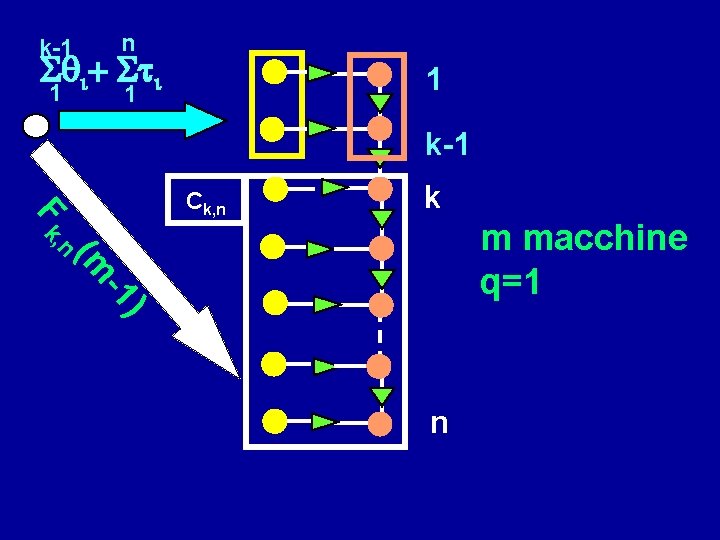
k-1 n 1 1 qi+ ti 1 k-1 k m macchine q=1 ) -1 (m n F k, Ck, n n

Ch, k sottografo indotto dalle sezioni da Sh a Sk Fk, n(p) : = lunghezza minima di un percorso critico sul pettine C P k, n, tra tutte le partizioni Pkn tali che |P|=p m,

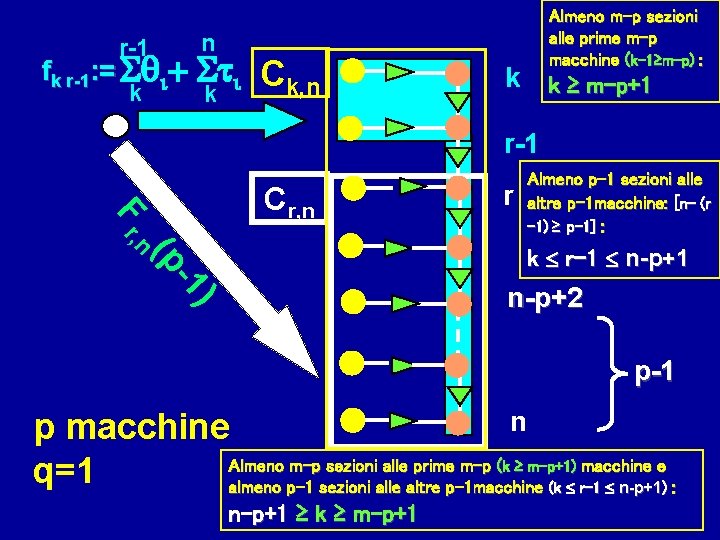
r-1 n fk r-1: = qi+ ti k k Ck, n Almeno m-p sezioni alle prime m-p macchine (k-1≥m-p) : k k ≥ m-p+1 r-1 F r, Cr, n r Almeno p-1 sezioni alle altre p-1 macchine: [n- (r -1) ≥ p-1] : (p n k r-1 n-p+1 1) n-p+2 p-1 n p macchine Almeno m-p sezioni alle prime m-p (k ≥ m-p+1) macchine e q=1 almeno p-1 sezioni alle altre p-1 macchine (k r-1 n-p+1) : n-p+1 ≥ k ≥ m-p+1

r-1 n k+1 r n-p+2 k k Fkn(p) = min {max{ qi+ ti ; Frn(p-1)}} fk r-1 m–p+1 k n–p+1 per ogni p ≥ 2, quindi, i valori possibili per k sono n-m+1 anche per p=m, ma interessa ovviamente solo k=1 Ne consegue che per ogni k la formula è valida per p min{m, n-k+1} Per il calcolo si comincia da: n Fkn(1) = i (ti + qi) m k n k

GRAFO DI CALCOLO DEGLI Fkn(p) Per organizzare il calcolo degli F può convenire un grafo orientato pesato in cui il peso dei nodi sorgente è assegnato e quello nj degli altri è determinato in base ai pesi ni , con i e d-j dei nodi predecessori (appartenenti cioè alla stella negativa d-j del nodo j) e i pesi aij dei relativi archi entranti secondo la formula nj = min { max[ aij; ni ] } i e d-j ni Fkn(p) = min {max[fkr-1 ; Frn(p-1)]} k+1 r n-p+2 aij nj aij Fn-p+2, n(p-1) ni fk, r-p+1 fk, r-1 ni Fkn(p) fkk Frn(p-1) Fk+1, n(p-1)

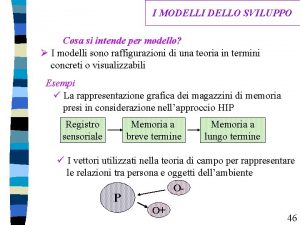
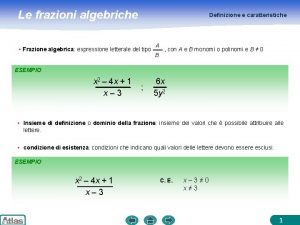
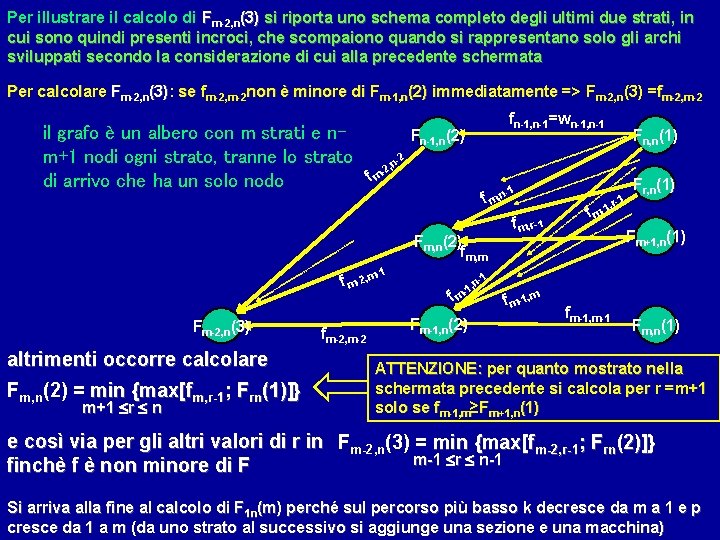
Applicando ricursivamente la formula Fn, n(1) fm-1, n-1 Frn(1) Fkn(p) = min {max[fkr-1 ; Frn(p-1)]} k+1 r n-p+2 fm-1, r-1 Fm-1, n(2) il primo confronto da fare è per il calcolo di fm-1, m-1 Fm, n(1) Fm-1, n(2) = min { max[ fm-1, r-1; Frn(1) ] } m r n All’aumentare di r, fkr-1 non diminuisce ed Frn(1) non aumenta, quindi per trovare il minimo bisogna aumentare r finchè f diventa non minore di F: se fm-1, m-1 ≥ Fmn(1), allora immediatamente => Fm-1, n(2) = fm-1, m-1; se, per r > m, fm-1, r-1 = Frn(1), allora immediatamente => Fm-1, n(2) = fm-1, m-1; se, fm-1, r-1 > Frn(1) => si riconsidera il confronto precedente e: Fm-1, n(2) = min { fm-1, r-1; Fr-1, n(1)} Per procedere quindi, in modo analogo, al calcolo di Fm-2, n(3) = min {max[fm-2, r-1; Frn(2)]} m-1 r n-1 bisogna tener conto (=>p. seguente) del fatto che, per un generico Fh+1, n(p), non occorre partire dal valore più basso di r, se si è gia colcolato Fh, n(p)

Fh+1, n(p) = min {max[fh+1, r-1 ; Frn(p-1)]} Fs+1, n(p-1) fh , s h+2 r n-p+2 Se s è il minimo valore tale che fh, s sia non fh+1, s-1 ≤ fh, s-1 < Fs, n(p-1) minore di Fs+1, n(p-1) allora nel calcolo di Fh+1, n(p) basta far crescere r dal , s 1 f h+ valore s+1, cioè 1 cominciare da fh+1, s : f h+1, s-1 Infatti fh+1, s-1 è non s , fh maggiore di fh, s-1, da cui si ottiene sottraendo il f h+1, s- i-1 tempo delle operazioni Fh+1, n(p) della sezione h, e quest’ultima è minore di Fs, n(p-1), per ipotesi. Inoltre le Fs-i, n(p) aumentano con i, mentre le fh+1, s-i-1 diminuiscono Fh, n(p) SVILUPPANDO GLI ARCHI DAL BASSO, NON OCCORRE SVILUPPARE QUELLI CHE INCROCIANO GLI ARCHI SVILUPPATI IN PRECEDENZA Fs, n(p-1) Fs-i, n(p-1) Fh-1, n(p-1)

Per illustrare il calcolo di Fm-2, n(3) si riporta uno schema completo degli ultimi due strati, in cui sono quindi presenti incroci, che scompaiono quando si rappresentano solo gli archi sviluppati secondo la considerazione di cui alla precedente schermata Per calcolare Fm-2, n(3): se fm-2, m-2 non è minore di Fm-1, n(2) immediatamente => Fm-2, n(3) =fm-2, m-2 fn-1, n-1=wn-1, n-1 il grafo è un albero con m strati e n. Fn-1, n(2) m+1 nodi ogni strato, tranne lo strato -2 , n -2 fm di arrivo che ha un solo nodo f m, n Fm, n(2) fm, m -1 f m-2, m Fm-2, n(3) altrimenti occorre calcolare Fm, n(2) = min {max[fm, r-1; Frn(1)]} m+1 r n fm-2, m-2 , n -1 fm Fm-1, n(2) Fn, n(1) 1 r-1 Fr, n(1) , f m, r-1 f m-1 Fm+1, n(1) -1 f m-1, m fm-1, m-1 Fm, n(1) ATTENZIONE: per quanto mostrato nella schermata precedente si calcola per r =m+1 solo se fm-1, m≥Fm+1, n(1) e così via per gli altri valori di r in Fm-2, n(3) = min {max[fm-2, r-1; Frn(2)]} m-1 r n-1 finchè f è non minore di F Si arriva alla fine al calcolo di F 1 n(m) perché sul percorso più basso k decresce da m a 1 e p cresce da 1 a m (da uno strato al successivo si aggiunge una sezione e una macchina)

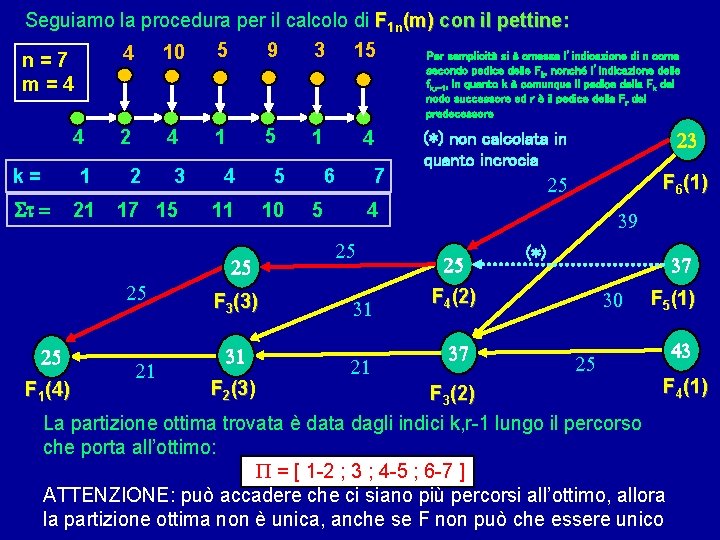
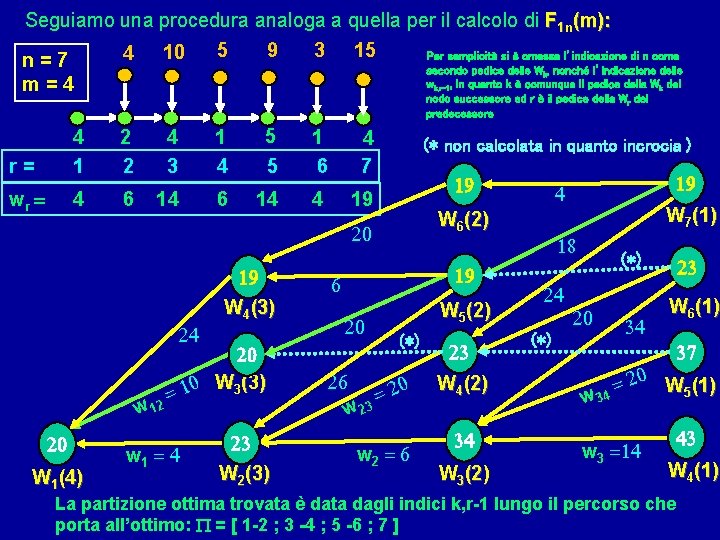
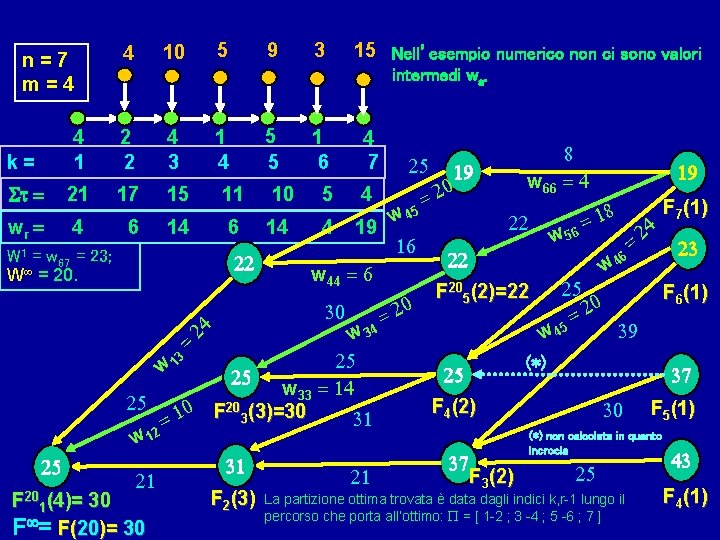
Seguiamo la procedura per il calcolo di F 1 n(m) con il pettine: 9 3 15 5 Per semplicità si è omessa l’indicazione di n come 4 10 n=7 secondo pedice delle F , nonché l’indicazione delle f , in quanto k è comunque il pedice della F del m=4 k k, r-1 nodo successore ed r è il pedice della Fr del predecessore 4 k= 1 t = 21 2 4 2 3 17 15 5 1 4 5 11 10 25 25 25 21 F 3(3) 31 1 4 6 7 5 23 (*) non calcolata in quanto incrocia F 6(1) 25 4 25 31 21 k 39 25 (*) 37 F 4(2) 37 30 25 F 5(1) 43 F 4(1) F 3(2) La partizione ottima trovata è data dagli indici k, r-1 lungo il percorso che porta all’ottimo: P = [ 1 -2 ; 3 ; 4 -5 ; 6 -7 ] ATTENZIONE: può accadere che ci siano più percorsi all’ottimo, allora la partizione ottima non è unica, anche se F non può che essere unico F 1(4) F 2(3)

Gantt delle macchine conseguente a una assegnazione di operazioni per la produzione di infiniti pezzi 4 4 10 5 9 2 4 1 5 1 11 15 20 0 M 1 M 2 M 3 M 4 5 8 3 15 4 26 30 Tempo di transito* = 30 Tempo di ciclo = 20 *Tempo di transito: dall’istante in cui entra una parte del pezzo a quello in cui il pezzo esce

infiniti pezzi (produzione continua): min tempo di ciclo=> min tempo per pezzo della macchina più carica: = W∞: = W 1 n(m) data P: wkn (P) : = tempo più elevato tra i pesi delle sezioni di C P kn, Wkn(p) : = min { wkn (P) } P |P|=p m , 1 k n

Analogamente a quanto visto per q=1, si ottiene: r-1 Wkn(p) = min {max{ i (qi+ ti) ; Wrn(p-1)}} k+1 r n-p+2 m–p+1 k n–p+1 2 p min{m, n-k+1} n Wkn(1) = i (ti + qi) k W = W 1 n(m) k wk r-1 è il tempo di lavoro della macchina p per ogni pezzo pari alla somma dei tempi delle operazioni delle sezioni da k a r-1 Sostituendo w a f e W a F si può impiegare un GRAFO DI CALCOLO analogo a quello già definito, facendo analoghe osservazioni sulla struttura del grafo e sulla possibilità di avere più di una P∞, pur essendo W unica

Seguiamo una procedura analoga a quella per il calcolo di F 1 n(m): 9 3 15 5 Per semplicità si è omessa l’indicazione di n come 4 10 n=7 secondo pedice delle W , nonché l’indicazione delle w , in quanto k è comunque il pedice della W del m=4 k k, r-1 nodo successore ed r è il pedice della Wr del predecessore 4 1 r= wr = 4 2 2 6 4 3 5 5 1 4 14 6 14 1 6 4 7 4 (* non calcolata in quanto incrocia ) 19 19 24 20 10 W 3(3) = 2 w 1 20 W 1(4) w 1 = 4 23 W 2(3) 19 6 20 W 5(2) (*) 26 20 = w 23 w 2 = 6 23 W 4(2) 34 W 3(2) 19 4 W 6(2) 20 19 W 4(3) k W 7(1) 18 24 (*) 20 34 (*) 23 W 6(1) 37 20 W (1) = 5 4 w 3 =14 43 W 4(1) La partizione ottima trovata è data dagli indici k, r-1 lungo il percorso che porta all’ottimo: P = [ 1 -2 ; 3 -4 ; 5 -6 ; 7 ]

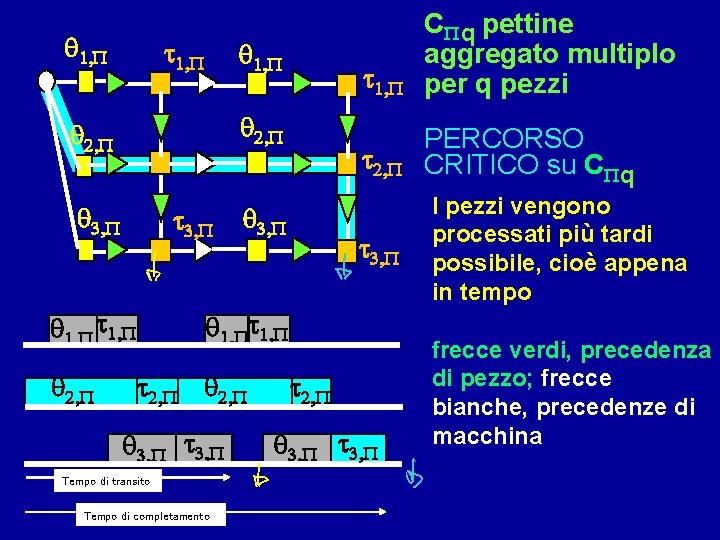
q 1, P t 1, P q 2, P q 3, P t 3, P q 1, P t 1, P q 2, P t 1, P CP q pettine aggregato multiplo per q pezzi t 2, P PERCORSO CRITICO su CP q t 3, P q 1, Pt 1, P t 2, P q 3, P t 3, P Tempo di transito Tempo di completamento t 2, P q 3, P t 3, P I pezzi vengono processati più tardi possibile, cioè appena in tempo frecce verdi, precedenza di pezzo; frecce bianche, precedenze di macchina

Tra i percorsi critici di CP q ne esiste almeno uno privo di ginocchia su CP[S] per s 1, s q Se si passa a sinistra di un percorso critico, così come indicato, si ha b a. Se si passa a destra si ha a b. Quindi a = b e i 3 percorsi sono tutti critici a b a a b s indice di pezzo [S] pettine aggregato per il pezzo S con la part. P ogni dorsale verticale è il pettine aggregato relativo a un pezzo: C

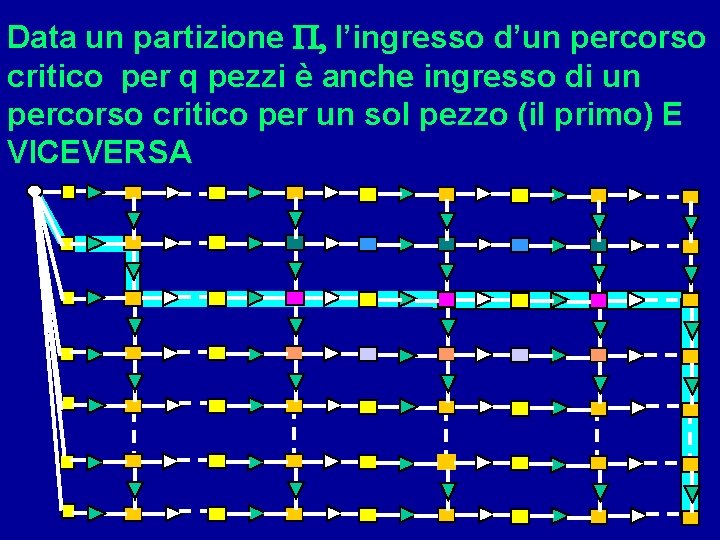
Data un partizione P, l’ingresso d’un percorso critico per q pezzi è anche ingresso di un percorso critico per un sol pezzo (il primo) E VICEVERSA

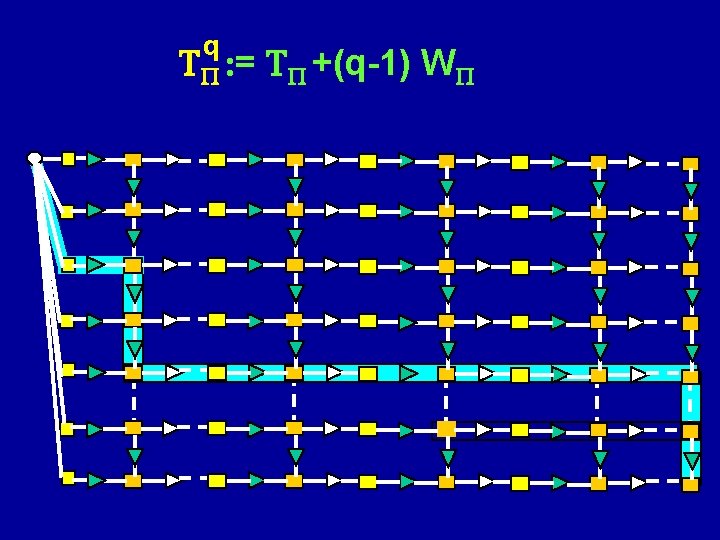
q TP : = TP +(q-1) WP

TP è tempo del percorso critico su CP WP : =max wi, P (carico di Mi con P) i= 1, . . , m q [TP : = TP +(q-1) WP] tempo del percorso q critico su CP , pettine aggregato multiplato q volte (q pezzi)

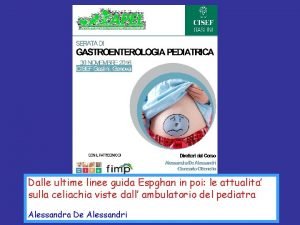
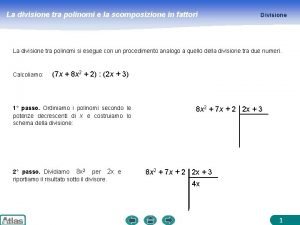
q q T : = min. P TP = min. P (TP +(q-1) WP) = min [ TP + (q-1)WP ] w Pw Pw: maxi wi. P = w

min [ TP + (q-1)WP ] = w Pw = min [min TP + (q-1)W] w Pw min TP = min TP : =F(w) Pw P: wi. P w

F 1 n (m) = min. P TP F(w) = [ F 1 n(m) : wi w ] q T = min { F(w) + (q-1)w } W Wq: Tq= F(Wq) + (q-1)Wq O(# {valori di w}) = O(n 2)

per calcolare F(w), si usa la stessa formula con un vincolo sull’escursione di r relativo al dato w n FW kn(p) = min{max{ wk r-1 + iti ; Frn(p-1)}} k+1 r n-p+2 wk r-1 = r r-1 i k (ti + qi) w wk r-1 è il tempo di lavoro totale delle operazioni relative ai denti da k a r-1 Il vincolo si inserisce facilmente nella procedura che impiega il GRAFO DI CALCOLO già usato

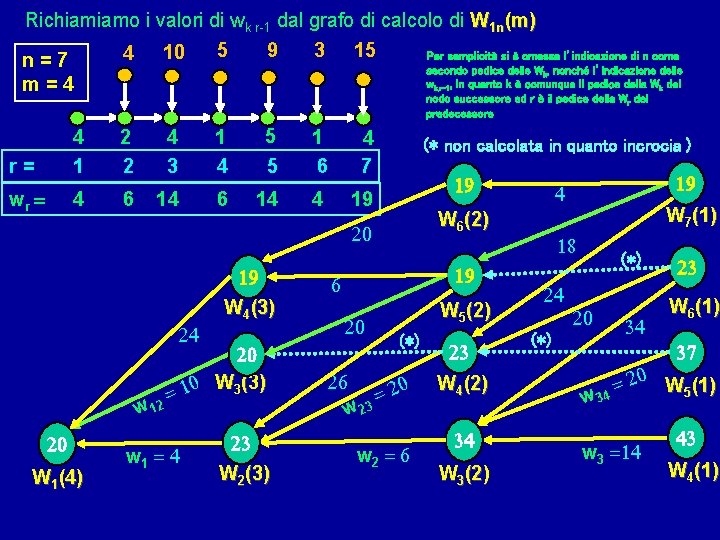
Richiamiamo i valori di wk r-1 dal grafo di calcolo di W 1 n(m) 9 3 15 5 Per semplicità si è omessa l’indicazione di n come 4 10 n=7 secondo pedice delle W , nonché l’indicazione delle w , in quanto k è comunque il pedice della W del m=4 k k, r-1 nodo successore ed r è il pedice della Wr del predecessore 4 1 r= wr = 4 2 2 6 4 3 5 5 1 4 14 6 14 1 6 4 7 4 (* non calcolata in quanto incrocia ) 19 19 24 20 10 W 3(3) = 2 w 1 20 W 1(4) w 1 = 4 23 W 2(3) 19 6 20 W 5(2) (*) 26 20 = w 23 w 2 = 6 23 W 4(2) 34 W 3(2) 19 4 W 6(2) 20 19 W 4(3) k W 7(1) 18 24 (*) 20 34 (*) 23 W 6(1) 37 20 W (1) = 5 4 w 3 =14 43 W 4(1)

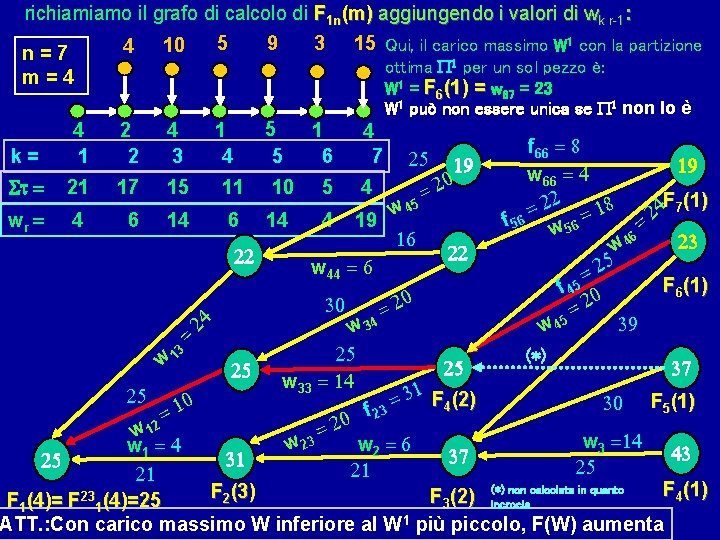
richiamiamo il grafo di calcolo di F 1 n(m) aggiungendo i valori di wk r-1: 9 3 15 Qui, il carico massimo W 1 con la partizione 5 10 4 n=7 ottima P 1 per un sol pezzo è: m=4 W 1 = F 6(1) = w 67 = 23 5 5 1 4 W 1 può non essere unica se P 1 non lo è k= 4 1 2 2 4 3 t = 21 17 15 11 10 5 4 wr = 4 6 14 4 19 22 24 1 6 4 7 25 w 45 16 w 44 = 6 30 0 =2 = 19 0 2 22 f 66 = 8 19 w 66 = 4 F 7(1) 22 8 4 1 = 2 f 56 w 56 = = 6 23 w 4 5 =2 F 6(1) f 45 0 =2 39 w 45 34 w = 3 25 (*) w 1 25 37 25 w 33 = 14 31 F (2) 25 = 0 30 F 5(1) 4 1 3 f 2 = 20 2 1 = w w 3 =14 w 2 = 6 w 23 w 1 = 4 43 37 31 25 25 21 21 non calcolata in quanto F 4(1) F 2(3) F 3(2) (*) F 1(4)= F 231(4)=25 incrocia ATT. : Con carico massimo W inferiore al W 1 più piccolo, F(W) aumenta

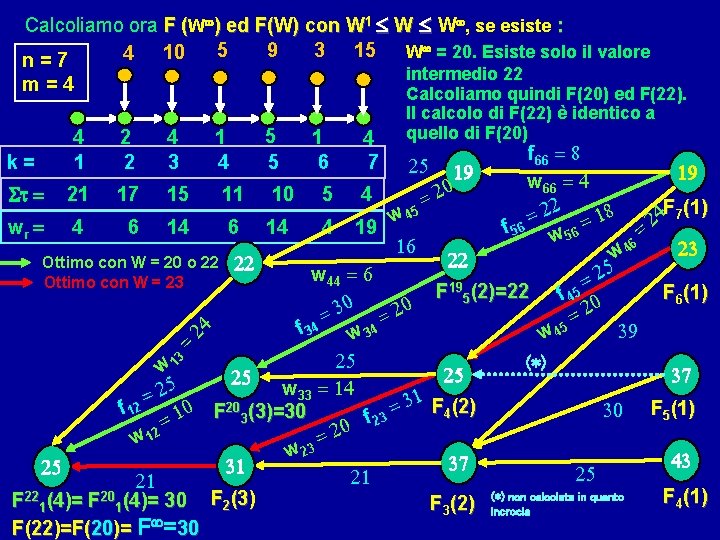
Calcoliamo ora F (W ) ed F(W) con W 1 W W , se esiste : 9 3 15 W = 20. Esiste solo il valore 5 4 10 n=7 m=4 4 1 2 2 4 3 1 4 5 5 1 6 4 7 intermedio 22 Calcoliamo quindi F(20) ed F(22). Il calcolo di F(22) è identico a quello di F(20) f 66 = 8 19 19 w = 4 66 0 t = 21 17 15 11 10 5 4 =2 F 7(1) 22 8 4 1 w 45 = 2 f 56 w 56 = wr = 4 6 14 4 19 = 6 16 23 w 4 22 Ottimo con W = 20 o 22 22 5 2 w 44 = 6 Ottimo con W = 23 = F 195(2)=22 F 6(1) f 45 0 0 3 2 20 = = = f 34 w 34 45 39 24 w = 3 25 (*) w 1 25 37 25 5 w = 14 2 33 = 31 F (2) 20 = f 12 0 30 F 5(1) 4 f 23 = 1 F 3(3)=30 20 = w 12 w 23 43 37 31 25 25 21 21 F 4(1) F 221(4)= F 201(4)= 30 F 2(3) F (2) (*) non calcolata in quanto k= F(22)=F(20)= F =30 30 25 3 incrocia

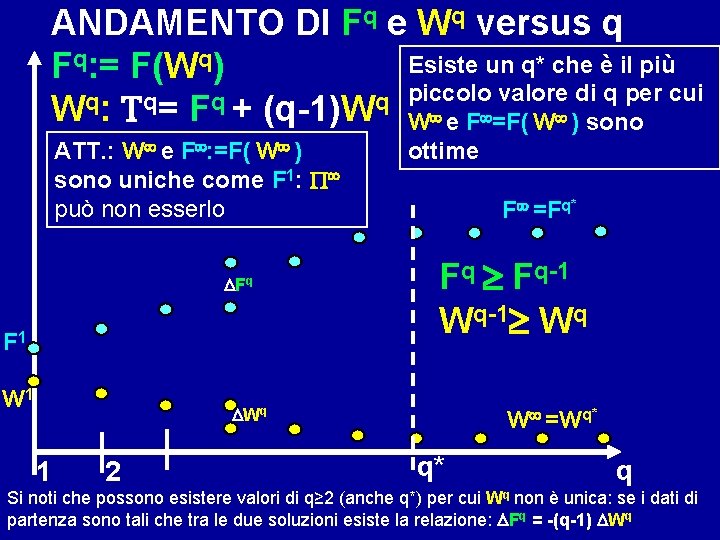
ANDAMENTO DI Fq e Wq versus q Esiste un q* che è il più Fq: = F(Wq) piccolo valore di q per cui q q W : T = F + (q-1)W W e F =F( W ) sono ATT. : W e F : =F( W ) sono uniche come F 1: P può non esserlo DFq F 1 W 1 ottime F =Fq* Fq Fq-1 Wq DWq 1 2 W =Wq* q* q Si noti che possono esistere valori di q≥ 2 (anche q*) per cui Wq non è unica: se i dati di partenza sono tali che tra le due soluzioni esiste la relazione: DFq = -(q-1) DWq

q*: num. pezzi che “saturano” le possibilità di migliorare la distribuzione delle operazioni alle macchine Conviene prima calcolare F : = F(W ). Se F 1=F si ha q*=1 e W 1=W si noti che P può non essere unica e ciascuna P può dar luogo a diverse F, la più piccola delle quali è F . Analogamente P 1 può non essere unica e, se q*=1, si può dar luogo a diverse W 1, la più piccola delle quali vale W Se F 1<F , allora q*>1 È IL PIÙ PICCOLO VALORE PER CUI, per tutte le possibili W, SI HA: F + (q*-1) W ≤ F(W)+(q*-1)W cioè il più piccolo intero per cui: q* ≥ 1+ [F - F(Whs)] / [Whs- W ] per tutte le coppie hs per cui [ Whs >W , F(W)]

Le possibili coppie sono anche relative alle Wa : = Whs < W 1 che risulta dalla P 1 travata. Quindi occorre scegliere h ed s tali che: W s < Whs : = i (ti + qi) < W 1 h Conviene prendere la Wa subito inferiore a W 1 e calcolare la relativa F (Wa): - se è uguale a F 1, si aggiorna il valore di W 1 e si prende quella ancora inferiore finchè non si ottiene Fe 2>F 1: se Fe 2 < F si rileva il relativo carico massimo We 2, che può essere inferiore alla Wa che si era posto come limite; se Fe 2 = F il relativo carico massimo è ovviamente W e non ci sono altre coppie; - quindi si prende la Wa subito inferiore a We 2 fino a ottenere, se esiste, altrimenti stop, F >Fe 3>Fe 2 e così via fino alla più piccola Wa>W. Come anche nel caso Fe 2 = F , può accadere che non ci siano valori intermedi tra la W 1, aggiornata eventualmente, e W.

n=7 m=4 4 9 5 10 3 15 Nell’esempio numerico non ci sono valori intermedi wa. 5 5 k= 4 1 2 2 4 3 1 4 t = 21 17 15 11 10 5 4 wr = 4 6 14 4 19 W 1 = w 67 = 23; W = 20. 22 24 1 6 4 7 25 w 45 16 w 44 = 6 30 0 =2 = 19 20 8 w 66 = 4 22 22 F 205(2)=22 w 56 19 8 =1 w 25 0 =2 46 = 24 F 7(1) 23 F 6(1) 45 39 34 w w = 3 25 (*) w 1 25 37 25 w 33 = 14 25 20 F 4(2) 0 30 F 5(1) 31 = 1 F 3(3)=30 (*) non calcolata in quanto w 12 incrocia 43 37 31 25 25 F 3(2) 21 21 F 4(1) F 2(3) La partizione ottima trovata è data dagli indici k, r-1 lungo il F 201(4)= 30 percorso che porta all’ottimo: P = [ 1 -2 ; 3 -4 ; 5 -6 ; 7 ] F = F(20)= 30

Posto Fe 1=F 1 e We 1=W 1, il valore di q* è il più piccolo intero per cui: q*≥ 1+ [F - Fei] /[Wei - W ] i = 1, 2, …. . Nell’esempio numerico q*= 1+intero_sup[(30 -25)/(23 -20)]=4 cioè non inferiore alle minoranti: 1+ [F - Fei] /[Wei - W ] per tutti i valori di i Se q*>2, per i valori di q intermedi, Wq=Wej e Fq=Fej si trovano per le j tali che: Fej + (q-1) Wej Fei + (q-1)Wei per i= 1, 2, . . . Se esiste solo We 1=W 1 allora Pq=Pe 1, Wq=We 1 e Fq=Fe 1 per ogni q<q*. Nell’esempio numerico P 3=P 2=Pe 1, etc. Per valori di i per cui nelle due diseguaglianze qui sopra vige l’eguale, anche Pei è ottima e DFq = -(q-1) DWq. Attenzione: se ciò è vero per q*, Pei è ottima per q*, ma non per q infinito, perché Wei < W per definizione!

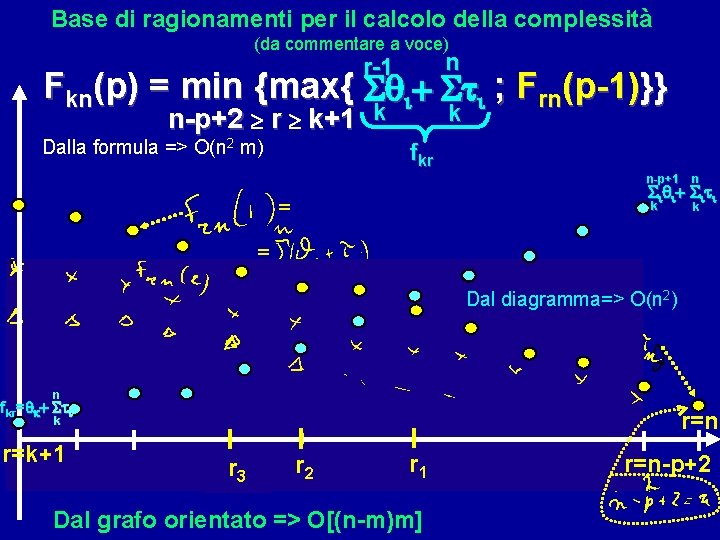
Base di ragionamenti per il calcolo della complessità (da commentare a voce) r-1 n n-p+2 r k+1 k k Fkn(p) = min {max{ qi+ ti ; Frn(p-1)}} Dalla formula => O(n 2 m) fkr n-p+1 n iqi+ iti = k k = Dal diagramma=> O(n 2) n fkr=qk+ ti r=n k r=k+1 r 3 r 2 r 1 Dal grafo orientato => O[(n-m)m] r=n-p+2