Controllo delle operazioni su una macchina Sequenziamento delle













- Slides: 24

Controllo delle operazioni su una macchina Sequenziamento delle operazioni a minimo: tempo di completamento medio, ritardo massimo, scarto minimo

Sequenziamento (Scheduling) delle operazioni magazzino con movimentazione interna controllo della successione dei tempi Ipotesi: tutti i grezzi sono disponibili dall’inizio (ri= 0)

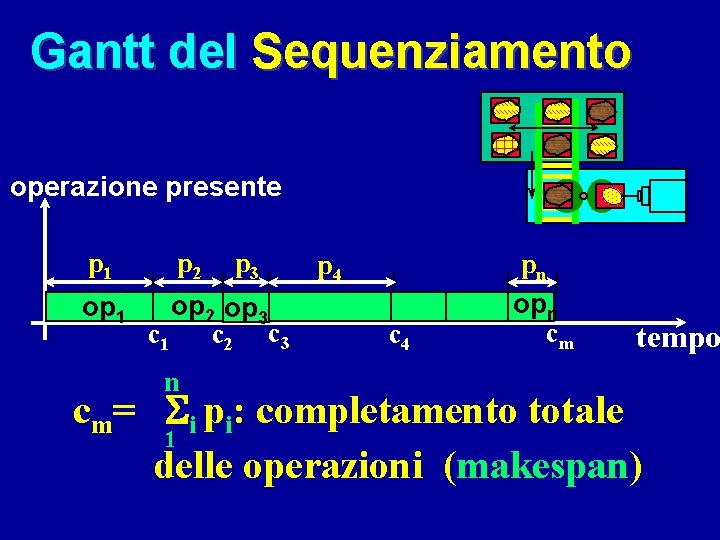
Gantt del Sequenziamento operazione presente p 1 op 1 p 2 p 3 op 2 op 3 c 1 c 2 c 3 n p 4 op 4 c 4 pn opn cm tempo cm= Si pi: completamento totale 1 delle operazioni (makespan)

op. p 1 op 1 p 2 p 3 p 4 op 2 op 3 c 1 c 2 c 3 c 4 pn opn cm 1 tempo 1 c = n Si ci: completamento medio n delle operazioni Si ci : somma dei tempi di completamento

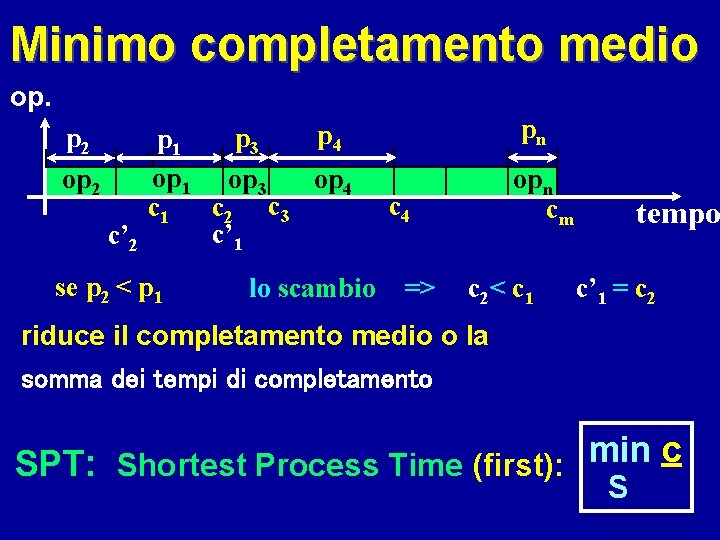
Minimo completamento medio op. p 2 op 2 p 4 p 3 p 1 op 3 op 4 c 1 c 2 c 3 c’ 1 c’ 2 se p 2 < p 1 lo scambio pn opn cm c 4 => c 2< c 1 tempo c’ 1 = c 2 riduce il completamento medio o la somma dei tempi di completamento min c SPT: Shortest Process Time (first): S

Minimo completamento medio presenza dell’operazione pn p 4 p 2 p 3 p 1 op 3 opn op 4 op 2 c 4 c 1 c 2 c 3 cm tempo c’ 1 c’ 2 lo scambio => se p 2/w 2 < p 1/w 1 c’ /w < c /w c’ 1/w 1= c 2/w 1 2 2 1 1 riduce la somma pesata dei tempi di completamento min Si ci/w 2 S SWPT: Shortest Weighted Process Time (first)

(ri= 0 => fi: = ci-ri = ci) SPT: p 3 pn op 3 opn c 3 cn p 2 op 2 c 2 p 4 op 4 cm Minimizza anche: - flusso medio F - attesa media W - num. medio p. in att. Nw

Nw(t) n-1 n c / c m= 1 + N w 2 1 cn ci n ck cj cy cx =cmt 1 Nw = c Sr x cr + cm- cm = n c / cm -1 m 1

SPT Massimizza: Numero medio ultimati Nu(t) n-1 2 1 ci cj 1 Nu = c ck cn cy cm n S (c c ) + c m- c m r i m r m 1 1 = cm ( ncm- nc ) = n(1 -c/ cm) t

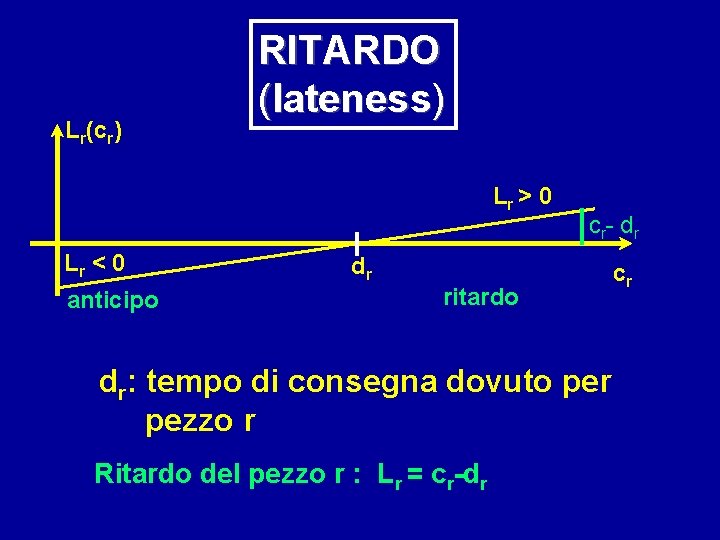
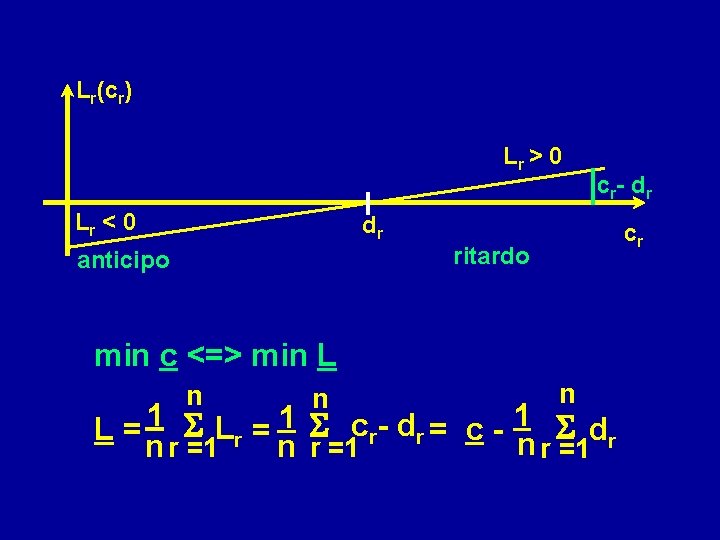
Lr(cr) RITARDO (lateness) Lr > 0 Lr < 0 anticipo cr- dr dr ritardo dr: tempo di consegna dovuto per pezzo r Ritardo del pezzo r : Lr = cr-dr cr

Lr(cr) Lr > 0 Lr < 0 c r- d r dr cr ritardo anticipo min c <=> min L n n n L = 1 S Lr = 1 S cr- dr = c - 1 n S dr n r =1

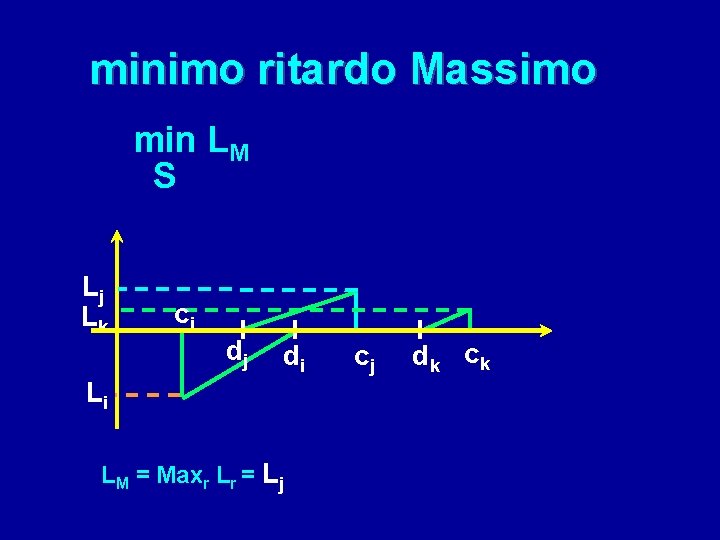
minimo ritardo Massimo min LM S Lj Lk ci dj di Li LM = Maxr Lr = Lj cj d k ck

Earliest Due Date EDD dati lavori J 1. . . Jn Si hanno le seguenti date di consegna: di (1) di (2) di (3) di (4) d i ( l)

Earliest Due Date EDD Si riordinano gli indici nell’ordine delle date dovute d 1 d 3 d 2 d 4 dn e si sequenziano i lavori nello stesso ordine J 1 J 3 J 2 d 1 d 2 Jn J 4 d 3 d 4 dn

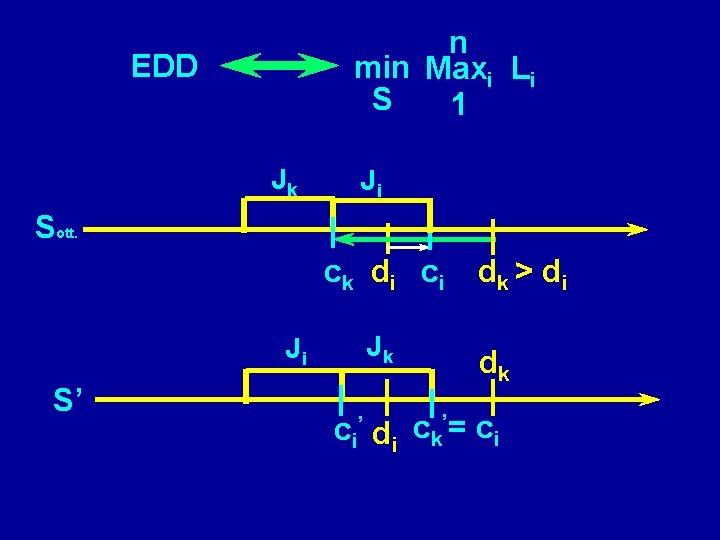
n min Maxi Li S 1 EDD Jk Ji Sott. ck d i ci Ji S’ Jk dk > d i dk c i ’ d i c k’ = c i

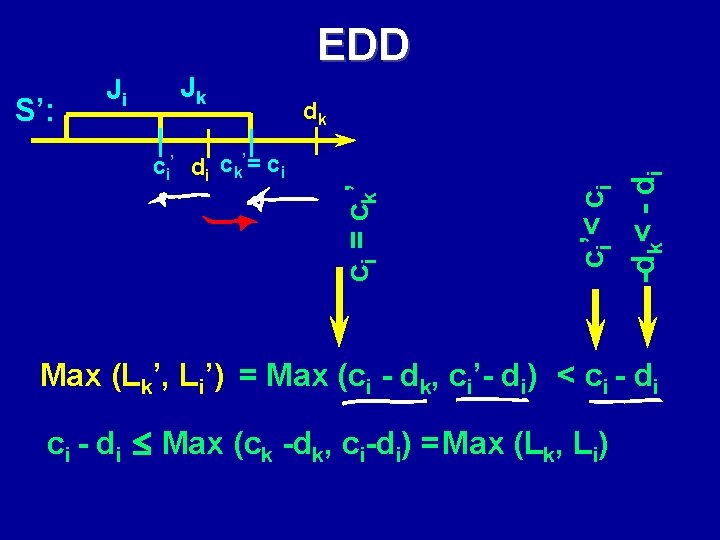
EDD -dk< - di c i ’ d i c k’ = c i dk ci’< ci Jk c i = c k’ S’: Ji Max (Lk’, Li’) = Max (ci - dk, ci’- di) < ci - di Max (ck -dk, ci-di) = Max (Lk, Li)

Earliest Due Date EDD n min Maxi Li : Massimo anticipo minimo S 1 : n Max mini Ai ci di Ai = -Li> 0 S 1 Ai < 0 ci di

Algoritmo di Moore per la minimizzazione dello scarto (numero di lavori, ciascuno di una sola operazione, in ritardo)

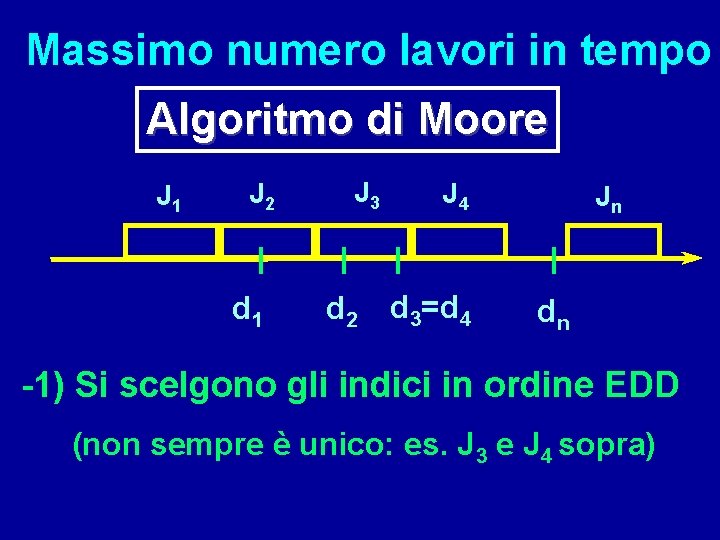
Massimo numero lavori in tempo Algoritmo di Moore J 1 J 2 d 1 J 3 d 2 J 4 d 3=d 4 Jn dn -1) Si scelgono gli indici in ordine EDD (non sempre è unico: es. J 3 e J 4 sopra)

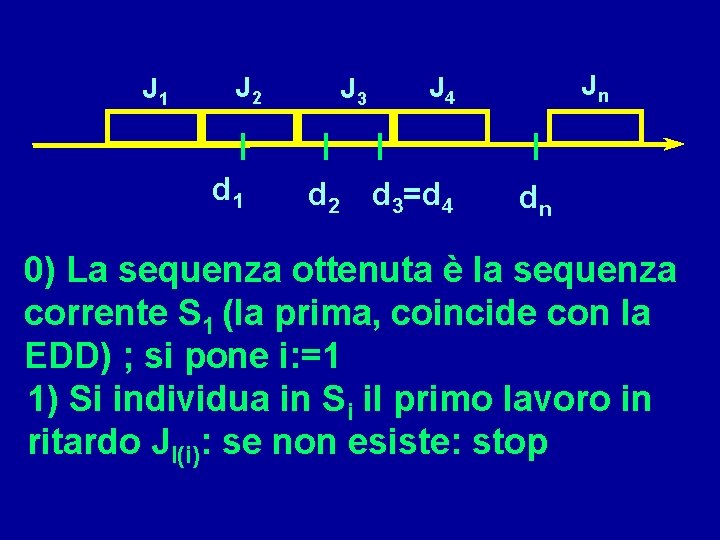
J 1 J 2 d 1 J 3 d 2 Jn J 4 d 3=d 4 dn 0) La sequenza ottenuta è la sequenza corrente S 1 (la prima, coincide con la EDD) ; si pone i: =1 1) Si individua in Si il primo lavoro in ritardo Jl(i): se non esiste: stop

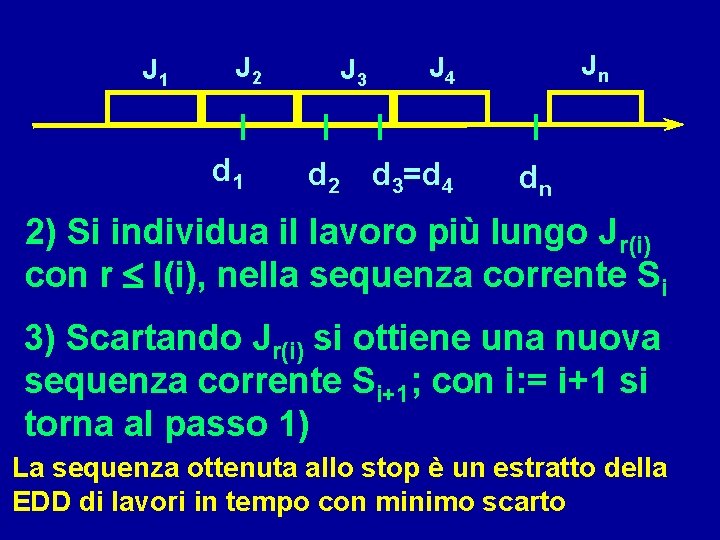
J 1 J 2 d 1 J 3 d 2 Jn J 4 d 3=d 4 dn 2) Si individua il lavoro più lungo Jr(i) con r l(i), nella sequenza corrente Si 3) Scartando Jr(i) si ottiene una nuova sequenza corrente Si+1; con i: = i+1 si torna al passo 1) La sequenza ottenuta allo stop è un estratto della EDD di lavori in tempo con minimo scarto

Dimostrazione di Moore 1968 d 1 d 2 … dn ( i lavori sono ordinati secondo EDD ) Si costruisce un estratto Mk del massimo numero, n. K k, di lavori terminati in tempo tra i primi k della EDD e con il minimo tempo totale di processamento (MK è quindi ottima per l’insieme dei primi k lavori e, tra quelle ottime, di lunghezza minima) Mn e’ una sequenza ottima (i lavori in ritardo sono scartati). nk : = massimo numero di lavori in tempo, cioè la dimensione di Mk [indici di Mk]: = { i(1), … i(nk) } sequenza dei lavori in tempo tra i primi k lavori nella EDD (nessuno scarto: i(h)=h, nk=k)

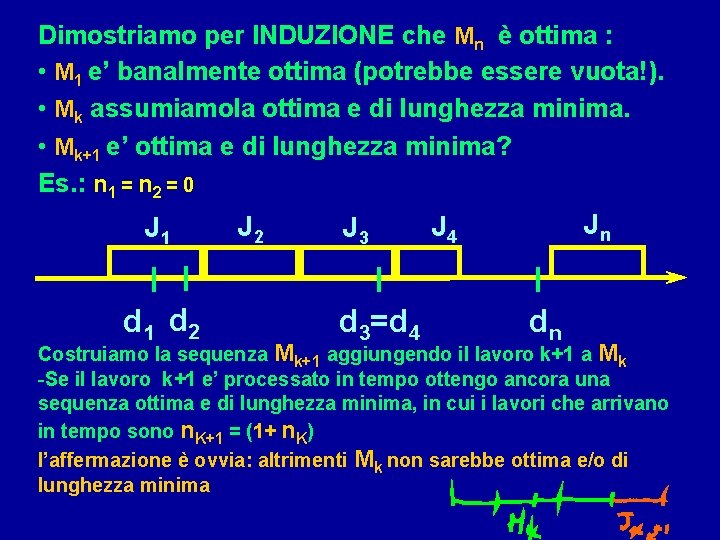
Dimostriamo per INDUZIONE che Mn è ottima : • M 1 e’ banalmente ottima (potrebbe essere vuota!). • Mk assumiamola ottima e di lunghezza minima. • Mk+1 e’ ottima e di lunghezza minima? Es. : n 1 = n 2 = 0 J 1 d 2 J 3 d 3=d 4 Jn J 4 dn Costruiamo la sequenza Mk+1 aggiungendo il lavoro k+1 a Mk -Se il lavoro k+1 e’ processato in tempo ottengo ancora una sequenza ottima e di lunghezza minima, in cui i lavori che arrivano in tempo sono n. K+1 = (1+ n. K) l’affermazione è ovvia: altrimenti Mk non sarebbe ottima e/o di lunghezza minima

- se k+1 non e’ processato in tempo, elimino uno dei lavori con tempo di processamento più lungo, fra gli (1+ nk). Ottengo una sequenza ottima di n. K+1= n. K lavori che arrivano in tempo, con tempo di processamento totale minimo. se il lavoro più lungo eliminato è quello aggiunto l’affermazione è ovvia: Mk è ottima perché n. K+1= n. K ; di lunghezza minima perché sostituendo un lavoro di Mk con il k+1 se ne ottiene una ottima più lunga altrimenti l’affermazione, ancorché intuitiva, va dimostrata: sia r con r k il lavoro eliminato e p(r) il suo tempo di processamento: la sequenza Mk senza r è un estratto di lunghezza minima con n. K – 1 lavori in tempo fra i primi k della EDD. Infatti è divisa in due segmenti: il primo segmento è un estratto del massimo numero di lavori in tempo tra i primi r-1 della EDD e il secondo segmento è un estratto del massimo numero di lavori in tempo tra quelli da r+1 a k della EDD: per avere un altro estratto con n. K – 1 lavori in tempo si dovrebbe sostiuire uno dei lavori di Mk con r che è di lunghezza massima. Alla sequenza Mk senza r si aggiunge il lavoro k+1 per dare una sequenza che è ottima (ha n. K+1= n. K lavori in tempo), di lunghezza minima (minore di Mk ), cioè è Mk+1 , in quanto k+1 è stato aggiunto ad un estratto di lunghezza minima con n. K – 1 lavori in tempo ed è più corto di r. In effetti andrebbe anche dimostrato che non serve recuperare i lavori scartati in M Chi è interessato veda la dimostra<ione di Francis riportata nel file dim MOORE. PPT
 Proprietà delle operazioni
Proprietà delle operazioni Macchina delle quarantore napoli
Macchina delle quarantore napoli La vita è come una macchina fotografica
La vita è come una macchina fotografica Leve e macchine semplici
Leve e macchine semplici Limiti
Limiti Operazioni con i monomi esercizi
Operazioni con i monomi esercizi Operazioni triangolari extra ue
Operazioni triangolari extra ue Le cifre significative
Le cifre significative Operazioni musicali
Operazioni musicali I monomi mappa concettuale
I monomi mappa concettuale Operazioni radicali
Operazioni radicali Notazione scientifica divisione
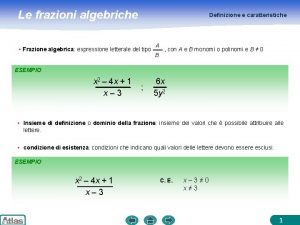
Notazione scientifica divisione Definizione di frazione algebrica
Definizione di frazione algebrica Indicatori di anomalia antiriciclaggio
Indicatori di anomalia antiriciclaggio Espressioni con esponente negativo
Espressioni con esponente negativo Operazioni coi vettori
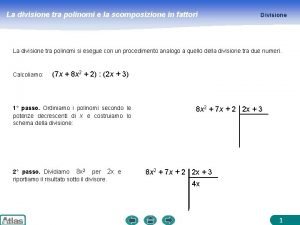
Operazioni coi vettori Raccoglimenti polinomi
Raccoglimenti polinomi Parti correlate nota integrativa
Parti correlate nota integrativa Proprietà distributiva
Proprietà distributiva Sotto forma di numero decimale
Sotto forma di numero decimale Cose moderne
Cose moderne La nascita delle lingue e delle letterature romanze
La nascita delle lingue e delle letterature romanze L'esperienza delle cose moderne e la lezione delle antique
L'esperienza delle cose moderne e la lezione delle antique Le prime macchine termiche
Le prime macchine termiche Grafico adiabatica
Grafico adiabatica