Lezione 5 Operazioni musicali nel sistema di rappresentazione

Lezione 5 Operazioni musicali nel sistema di rappresentazione binomiale Programmazione per la Musica | Prof. Luca A. Ludovico

Coppie <pc, nc> ammissibili Sulle colonne sono disposte le note con lo stesso nome e diverso stato di alterazione (sempre 5), sulle righe le enarmonie (sempre 3, ad eccezione di G#/Ab). Quante sono le possibili combinazioni? Teoricamente 12 ∙ 7 = 84, ossia tutte le celle nella tabella a fianco In pratica, considerando al più le doppie alterazioni, 7 ∙ 5 = 35. Fino ad alterazioni quintuple non ci sarebbe ambiguità (vedi colonna C). 0 1 0 C D√ B# 1 C# D¯ B� 2 C� D E√ 3 C� # D# E¯ F√ 4 C�� D� E F¯ 5 C�� # E# F G√ E� F# G¯ F� G A√ pc nc 2 3 4 5 6 6 ? 7 C√√¯ 8 C√√ G# A¯ 9 C√ ¯ G� A B√ 10 C√ A# B¯ 11 C¯ A� B Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

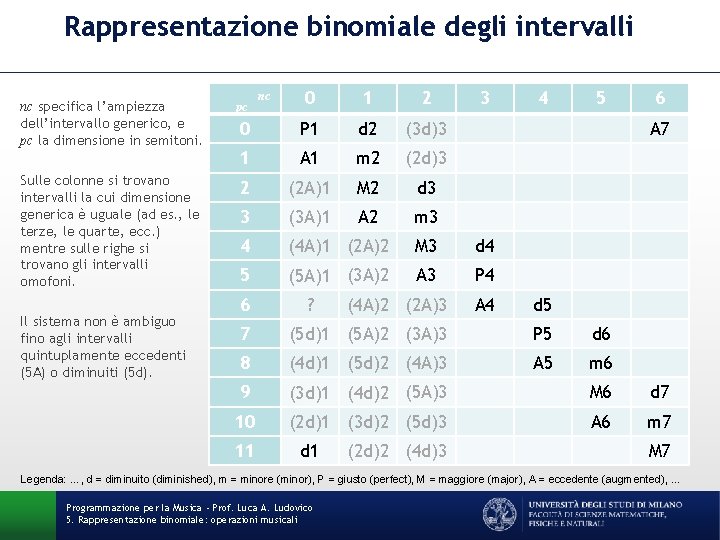
Rappresentazione binomiale degli intervalli 0 1 2 0 P 1 d 2 (3 d)3 1 A 1 m 2 (2 d)3 2 (2 A)1 M 2 d 3 3 (3 A)1 A 2 m 3 4 (4 A)1 (2 A)2 M 3 d 4 5 (5 A)1 (3 A)2 A 3 P 4 nc specifica l’ampiezza dell’intervallo generico, e pc la dimensione in semitoni. pc Sulle colonne si trovano intervalli la cui dimensione generica è uguale (ad es. , le terze, le quarte, ecc. ) mentre sulle righe si trovano gli intervalli omofoni. Il sistema non è ambiguo fino agli intervalli quintuplamente eccedenti (5 A) o diminuiti (5 d). 6 nc ? (4 A)2 (2 A)3 3 4 5 6 A 7 A 4 d 5 7 (5 d)1 (5 A)2 (3 A)3 P 5 d 6 8 (4 d)1 (5 d)2 (4 A)3 A 5 m 6 9 (3 d)1 (4 d)2 (5 A)3 M 6 d 7 10 (2 d)1 (3 d)2 (5 d)3 A 6 m 7 11 d 1 (2 d)2 (4 d)3 M 7 Legenda: …, d = diminuito (diminished), m = minore (minor), P = giusto (perfect), M = maggiore (major), A = eccedente (augmented), … Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Un’osservazione • Nelle lezioni precedenti abbiamo visto operazioni aritmetiche coinvolgono contemporaneamente rappresentazioni binomiali di altezze e di intervalli. – Ad esempio, il calcolo dell’intervallo determinato da due note si effettua attraverso una differenza di <pc, nc> relativi ad altezze, e il risultato è una coppia <pc, nc> relativa ad un intervallo. • Questo mescolamento di concetti musicali differenti è giustificato dal fatto che le altezze stesse, viste nel sistema binomiale, possano essere viste anche come intervalli rispetto al riferimento <0, 0> assegnato convenzionalmente al Do naturale. • Ad esempio, <2, 1> è la rappresentazione binomiale tanto dell’altezza della nota Re naturale quanto dell’intervallo di 2 a magg. che permette di passare dal Do naturale al Re naturale. Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Trasposizione cromatica e diatonica • Nei software di editing digitale della partitura (ad es. Finale) si è soliti distinguere tra: – traspozione diatonica, ossia di un certo numero di gradi sulla scala corrente; – trasposizione cromatica, ossia di un certo numero di semitoni • Nel primo caso, la trasposizione viene dimensionata attraverso il solo parametro di distanza dell’intervallo. Ad es. , trasporre di una quinta significa traslare tutti i gradi della scala di +4 (la tonica diventa dominante, il sesto grado abbassato diventa un terzo grado abbassato, ecc. ) • Nel secondo caso, si usa la definizione completa di intervallo, ossia distanza più specie. Ad es. , si traspone di una terza minore. Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Esempi di trasposizione diatonica Trasposizione diatonica di una quarta ascendente La scala di Do magg. da tonica (I grado) diventa una scala di Do magg. da sottodominante (IV grado) Trasposizione diatonica di una terza ascendente Il IV grado alterato in senso ascendente diventa un sesto grado alterato in senso ascendente Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Esempi di trasposizione cromatica Trasposizione cromatica di una quarta giusta ascendente La scala di Do magg. diventa una scala di Fa magg. Trasposizione cromatica di una terza minore ascendente Ogni nota viene trasposta secondo un valore di name class e pitch class. Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Operatori musicali: trasposizione • Tutte le operazioni viste nei sistemi pc e nc sono possibili anche in rappresentazione binomiale: vengono eseguite separatamente sulle componenti pc in modulo 12 e nc in modulo 7. • La trasposizione corrisponde all’addizione. Trasporre una nota <a, b> di un intervallo <c, d> significa: <a, b> + <c, d> = <(a + c) mod 12, (b + d) mod 7> • Esempio: trasporre D (Re naturale) di una terza maggiore <2, 1> + <4, 2> = <6, 3> D + M 3 = F# • La trasposizione può avvenire in senso discendente. Trasporre di una terza maggiore discendente implica sommare <-4, -2> Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Proprietà della trasposizione nel sistema binomiale • Sia U l’insieme universo costituito dalle 84 classi di altezze binomiali, ottenibili come combinazione dei 7 valori ammessi per nc e dei 12 valori ammessi per pc. Siano A, B e C tre binomi qualsiasi U. • • • (A + B) U A+B=B+A la somma è commutativa (A + B) + C = A + (B + C) la somma è associativa <0, 0> è l’elemento neutro per l’addizione, in quanto A + <0, 0> = A Per ogni A esiste un inverso A’ tale che A’ + A = <0, 0> L’inversione di <a, b> è <a, b>’ = <0, 0> – <a, b> = <(– a) mod 12, (– b) mod 7> e poiché <0, 0> = <12, 7> allora <a, b>’ = <(12 – a) mod 12, (7 – b) mod 7> Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Operatori musicali: calcolo dell’intervallo • Per determinare l’intervallo tra due note, si sottrae la prima nota dalla seconda. Tale calcolo corrisponde all’operazione di sottrazione. • Calcolare l’intervallo tra le note <c, d> e <a, b> significa: <a, b> – <c, d> = <(a – c) mod 12, (b – d) mod 7> • Esempio: l’intervallo tra Eb (Mi bemolle) e A (La naturale) è <9, 5> – <3, 2> = <6, 3> A - Eb = A 4 [quarta eccedente] • Invertendo gli estremi dell’intervallo: <3, 2> – <9, 5> = <6, 4> Eb – A = d 5 [quinta diminuita] Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Operatori musicali: inversione dell’intervallo • Come specificato sopra, l’inversione di un generico intervallo <a, b> è <a, b>’ = <12, 7> – <a, b> = <(12 – a) mod 12, (7 – b) mod 7> • Attenzione: apparentemente l’operazione è simile al calcolo di un intervallo, in quanto implica la differenza tra due binomi. In questo caso però la rappresentazione binomiale codifica intervalli e non altezze delle note. • Esempio: l’inversione di una quarta giusta è <12, 7> – <5, 3> = <7, 4> P 4 [4 a giusta] P 5 [5 a giusta] Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Operatori musicali: inversione melodica • L’inversione melodica di una sequenza è la sottrazione di ciascuna nota della sequenza da una costante binomiale • Esempio: inversione melodica rispetto alla costante <4, 2> Si osservi che pc e nc della costante binomiale divisi per 2 rappresentano l’altezza della nota (se esiste) rispetto la quale avviene l’inversione. – Nell’esempio, si tratta proprio della prima nota della sequenza. D E <2, 1> <4, 2> - F# A C <6, 3> <9, 5> <0, 0> <4, 2> - <2, 1> = <4, 2> = <6, 3> = <9, 5> = <0, 0> = <2, 1> <0, 0> <10, 6> <7, 4> <4, 2> D C B¯ G E Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

Operatori musicali: prodotto • Si definisca ora l’operatore × nel seguente modo: <a, b> × <c, d> = <(a × c) mod 12, (b × d) mod 7> • • • (A x B) U A×B=B×A il prodotto è commutativo (A × B) × C = A × (B × C) il prodotto è associativo <1, 1> è l’elemento neutro per il prodotto, in quanto A × <1, 1> = A La moltiplicazione è distributiva rispetto alla somma: A × (B + C) = (A × B) + (A × C) (A + B) × C = (A × C) + (B × C) • Le proprietà qui elencate, più le proprietà della somma, sono sufficienti per dimostrare che si tratta di un anello commutativo con identità. Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

ESEMPI Cbr. Stats. java Il software legge in ingresso una sequenza di valori numerici interi codificati come Continuous Binomial Representation, e calcola: • la frequenza (espressa in Hz) del pitch più acuto • la frequenza (espressa in Hz) del pitch più grave • la frequenza media dei pitch. Osservazione: ci si sta concentrando sull’aspetto acustico delle note (le frequenze in Hertz) Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali

ESERCIZIO Si scriva un programma che richieda in ingresso una sequenza di pitch, espressi come cbr, e produca in uscita (in formato cbr) una trasposizione diatonica, ossia di un certo numero di gradi della scala • • • es. : T-7(C#3, A 5, B 4, G#6) cbr: 3010, 5095, 4116, 6084 = → C#2, A 4, B 3, G#5 es. : T 1(C#3, A 5, B 4, G#6) cbr: 3010, 5095, 4116, 6084 = → D#3, B 5, C 5, A#6 es. : T 2(C#3, A 5, B 4, G#6) cbr: 3010, 5095, 4116, 6084 = → E#3, C 6, D 5, B#6 Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali 2010, 4095, 3116, 5084 3031, 5116, 5000, 6105 3052, 6000, 5021, 6006

ESERCIZIO Si scriva un programma che richieda in ingresso una sequenza di pitch, espressi come cbr, e produca in uscita (in formato cbr) una tra le possibili scritture enarmoniche di ciascuna nota, limitandosi al più alle alterazioni doppie. Osservazione: in input sono ammesse scritture che vanno oltre le alterazioni doppie! Ad esempio E(C#3, A 5, B 4, G#6) = D¯ 3, B¯¯ 5, C¯ 5, A¯ 6 oppure E(C#3, A 5, B 4, G#6) = B� 2, G� 5, A� 4, A¯ 6 Programmazione per la Musica - Prof. Luca A. Ludovico 5. Rappresentazione binomiale: operazioni musicali