PLANTWIDE CONTROL How to design the control system













































- Slides: 71

PLANTWIDE CONTROL How to design the control system for a complete plant in a systematic manner Sigurd Skogestad Department of Chemical Engineering Norwegian University of Science and Tecnology (NTNU) Trondheim, Norway Singapore / Petronas / Petrobras, March 2010, India 2010 1

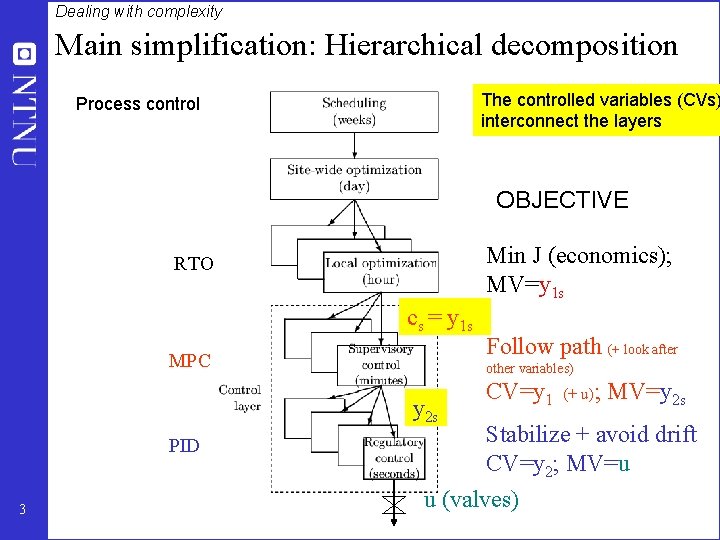
Dealing with complexity Main simplification: Hierarchical decomposition The controlled variables (CVs) interconnect the layers Process control OBJECTIVE Min J (economics); MV=y 1 s RTO cs = y 1 s MPC other variables) y 2 s PID 3 Follow path (+ look after CV=y 1 (+ u); MV=y 2 s Stabilize + avoid drift CV=y 2; MV=u u (valves)

Summary and references • The following paper summarizes the procedure: – S. Skogestad, ``Control structure design for complete chemical plants'', Computers and Chemical Engineering, 28 (1 -2), 219 -234 (2004). • There are many approaches to plantwide control as discussed in the following review paper: – T. Larsson and S. Skogestad, ``Plantwide control: A review and a new design procedure'' Modeling, Identification and Control, 21, 209 -240 (2000). 4

• • • • • • 5 • • S. Skogestad ``Plantwide control: the search for the self-optimizing control structure'', J. Proc. Control, 10, 487 -507 (2000). S. Skogestad, ``Self-optimizing control: the missing link between steady-state optimization and control'', Comp. Chem. Engng. , 24, 569575 (2000). I. J. Halvorsen, M. Serra and S. Skogestad, ``Evaluation of self-optimising control structuresfor an integrated Petlyuk distillation column'', Hung. J. of Ind. Chem. , 28, 11 -15 (2000). T. Larsson, K. Hestetun, E. Hovland, and S. Skogestad, ``Self-Optimizing Control of a Large-Scale Plant: The Tennessee Eastman Process'', Ind. Eng. Chem. Res. , 40 (22), 4889 -4901 (2001). K. L. Wu, C. C. Yu, W. L. Luyben and S. Skogestad, ``Reactor/separatorprocesses with recycles-2. Design for composition control'', Comp. Chem. Engng. , 27 (3), 401 -421 (2003). T. Larsson, M. S. Govatsmark, S. Skogestad, and C. C. Yu, ``Control structureselection for reactor, separator andrecycle processes'', Ind. Eng. Chem. Res. , 42 (6), 1225 -1234 (2003). A. Faanes and S. Skogestad, ``Buffer Tank Design for Acceptable Control Performance'', Ind. Eng. Chem. Res. , 42 (10), 2198 -2208 (2003). I. J. Halvorsen, S. Skogestad, J. C. Morud and V. Alstad, ``Optimal selection of controlled variables'', Ind. Eng. Chem. Res. , 42 (14), 3273 -3284 (2003). A. Faanes and S. Skogestad, ``p. H-neutralization: integrated process and control design'', Computers and Chemical Engineering, 28 (8), 1475 -1487 (2004). S. Skogestad, ``Near-optimal operation by self-optimizing control: From process control to marathonrunning and business systems'', Computers and Chemical Engineering, 29 (1), 127 -137 (2004). E. S. Hori, S. Skogestad and V. Alstad, ``Perfect steady-state indirect control'', Ind. Eng. Chem. Res, 44 (4), 863 -867 (2005). M. S. Govatsmarkand S. Skogestad, ``Selection of controlled variables and robust setpoints'', Ind. Eng. Chem. Res, 44 (7), 2207 -2217 (2005). V. Alstad and S. Skogestad, ``Null Space Method for Selecting Optimal Measurement Combinations as. Controlled Variables'', Ind. Eng. Chem. Res, 46 (3), 846 -853 (2007). S. Skogestad, ``The dos and don'ts of distillation columns control'', Chemical Engineering Research and Design (Trans IChem. E, Part A), 85 (A 1), 13 -23 (2007). E. S. Hori and S. Skogestad, ``Selection of control structureand temperaturelocation for two-product distillation columns'', Chemical Engineering Research and Design (Trans IChem. E, Part A), 85 (A 3), 293 -306 (2007). A. C. B. Araujo, M. Govatsmarkand S. Skogestad, ``Application of plantwide control to the HDA process. I Steady-state and selfoptimizing control'', Control Engineering Practice, 15, 1222 -1237 (2007). A. C. B. Araujo, E. S. Hori and S. Skogestad, ``Application of plantwide control to the HDA process. Part IIRegulatory control'', Ind. Eng. Chem. Res, 46 (15), 5159 -5174 (2007). V. Kariwala, S. Skogestad and J. F. Forbes, ``Reply to ``Further. Theoretical results on Relative Gain Array for Norn-Bounded Uncertain systems''''Ind. Eng. Chem. Res, 46 (24), 8290 (2007). V. Lersbamrungsuk, T. Srinophakun, S. Narasimhanand S. Skogestad, ``Control structuredesign for optimal operation of heat exchanger networks'', AICh. E J. , 54 (1), 150 -162 (2008). DOI 10. 1002/aic. 11366 T. Lid and S. Skogestad, ``Scaled steady state models for effective on-line applications'', Computers and Chemical Engineering, 32, 990 -999 (2008). T. Lid and S. Skogestad, ``Data reconciliation and optimal operation of a catalytic naphthareformer'', Journal of Process Control, 18, 320 -331 (2008). E. M. B. Aske, S. Strand S. Skogestad, ``Coordinator. MPC for maximizing plant throughput'', Computers and Chemical Engineering, 32, 195 -204 (2008). A. Araujo and S. Skogestad, ``Control structuredesign for the ammonia synthesis process'', Computers and Chemical Engineering, 32 (12), 2920 -2932 (2008). E. S. Hori and S. Skogestad, ``Selection of controlled variables: Maximum gain rule and combination of measurements'', Ind. Eng. Chem. Res, 47 (23), 9465 -9471 (2008). V. Alstad, S. Skogestad and E. S. Hori, ``Optimal measurement combinations as controlled variables'', Journal of Process Control, 19, 138 -148 (2009) E. M. B. Aske and S. Skogestad, ``Consistent inventory control'', Ind. Eng. Chem. Res, 48 (44), 10892 -10902 (2009).

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Define operational objective (cost) and constraints Step 2: Identify degrees of freedom and optimizate for disturbances Step 3: What to control ? (primary CV’s) (self-optimizing control) Step 4: Where set the production rate? (Inventory control) II Bottom Up • Step 5: Regulatory control: What more to control (secondary CV’s) ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 6

Main message • 1. Control for economics (Top-down steady-state arguments) – Primary controlled variables c = y 1 : • • • Control active constraints For remaining unconstrained degrees of freedom: Look for “self-optimizing” variables 2. Control for stabilization (Bottom-up; regulatory PID control) – Secondary controlled variables y 2 (“inner cascade loops”) • • 7 Control variables which otherwise may “drift” Both cases: Control “sensitive” variables (with a large gain)!

Idealized view of control (“Ph. D. control”) 8

Practice: Tennessee Eastman challenge problem (Downs, 1991) (“PID control”) 9

How we design a control system for a complete chemical plant? • • 10 Where do we start? What should we control? and why? etc.

• Alan Foss (“Critique of chemical process control theory”, AICh. E Journal, 1973): The central issue to be resolved. . . is the determination of control system structure. Which variables should be measured, which inputs should be manipulated and which links should be made between the two sets? There is more than a suspicion that the work of a genius is needed here, for without it the control configuration problem will likely remain in a primitive, hazily stated and wholly unmanageable form. The gap is present indeed, but contrary to the views of many, it is theoretician who must close it. • Carl Nett (1989): Minimize control system complexity subject to the achievement of accuracy specifications in the face of uncertainty. 11

Control structure design • Not the tuning and behavior of each control loop, • But rather the control philosophy of the overall plant with emphasis on the structural decisions: – – Selection of controlled variables (“outputs”) Selection of manipulated variables (“inputs”) Selection of (extra) measurements Selection of control configuration (structure of overall controller that interconnects the controlled, manipulated and measured variables) – Selection of controller type (LQG, H-infinity, PID, decoupler, MPC etc. ). • That is: Control structure design includes all the decisions we need make to get from ``PID control’’ to “Ph. D” control 12

Process control: “Plantwide control” = “Control structure design for complete chemical plant” • • Large systems Each plant usually different – modeling expensive Slow processes – no problem with computation time Structural issues important – What to control? Extra measurements, Pairing of loops Previous work on plantwide control: 13 • Page Buckley (1964) - Chapter on “Overall process control” (still industrial practice) • Greg Shinskey (1967) – process control systems • Alan Foss (1973) - control system structure • Bill Luyben et al. (1975 - ) – case studies ; “snowball effect” • George Stephanopoulos and Manfred Morari (1980) – synthesis of control structures for chemical processes • Ruel Shinnar (1981 - ) - “dominant variables” • Jim Downs (1991) - Tennessee Eastman challenge problem • Larsson and Skogestad (2000): Review of plantwide control

• Control structure selection issues are identified as important also in other industries. Professor Gary Balas (Minnesota) at ECC’ 03 about flight control at Boeing: The most important control issue has always been to select the right controlled variables --- no systematic tools used! 14

Main objectives control system 1. Stabilization 2. Implementation of acceptable (near-optimal) operation ARE THESE OBJECTIVES CONFLICTING? • Usually NOT – Different time scales • Stabilization fast time scale – Stabilization doesn’t “use up” any degrees of freedom • • 15 Reference value (setpoint) available for layer above But it “uses up” part of the time window (frequency range)

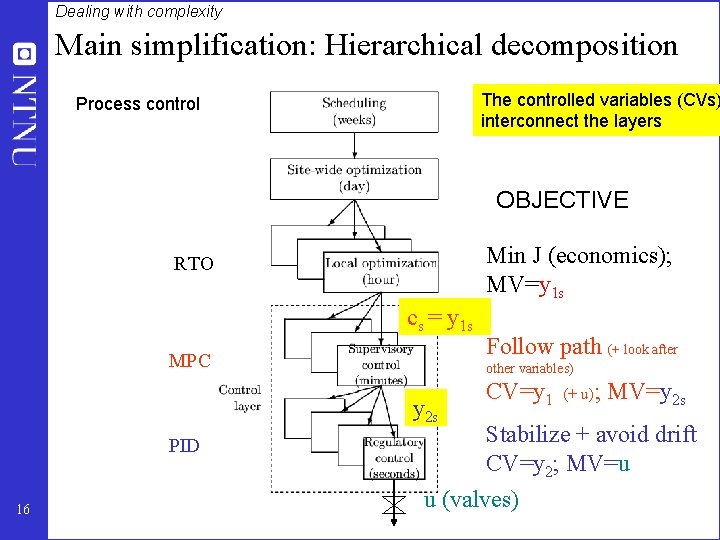
Dealing with complexity Main simplification: Hierarchical decomposition The controlled variables (CVs) interconnect the layers Process control OBJECTIVE Min J (economics); MV=y 1 s RTO cs = y 1 s MPC other variables) y 2 s PID 16 Follow path (+ look after CV=y 1 (+ u); MV=y 2 s Stabilize + avoid drift CV=y 2; MV=u u (valves)

Hierarchical decomposition Example: Bicycle riding Note: design starts from the bottom • Regulatory control: – First need to learn to stabilize the bicycle • CV = y 2 = tilt of bike • MV = body position • Supervisory control: – Then need to follow the road. • CV = y 1 = distance from right hand side • MV=y 2 s – Usually a constant setpoint policy is OK, e. g. y 1 s=0. 5 m • Optimization: – Which road should you follow? – Temporary (discrete) changes in y 1 s 17

Summary: The three layers • Optimization layer (RTO; steady-state nonlinear model): • • Supervisory control (MPC; linear model with constraints): • • • Identifies active constraints and computes optimal setpoints for primary controlled variables (y 1). Follow setpoints for y 1 (usually constant) by adjusting setpoints for secondary variables (MV=y 2 s) Look after other variables (e. g. , avoid saturation for MV’s used in regulatory layer) Regulatory control (PID): • Stabilizes the plant and avoids drift, in addition to following setpoints for y 2. MV=valves (u). Problem definition and overall control objectives (y 1, y 2) starts from the top. Design starts from the bottom. A good example is bicycle riding: • Regulatory control: • • Supervisory control: • 21 • First you need to learn how to stabilize the bicycle (y 2) Then you need to follow the road. Usually a constant setpoint policy is OK, for example, stay y 1 s=0. 5 m from the right hand side of the road (in this case the "magic" self-optimizing variable is y 1=distance to right hand side of road) Optimization: • Which road (route) should you follow?

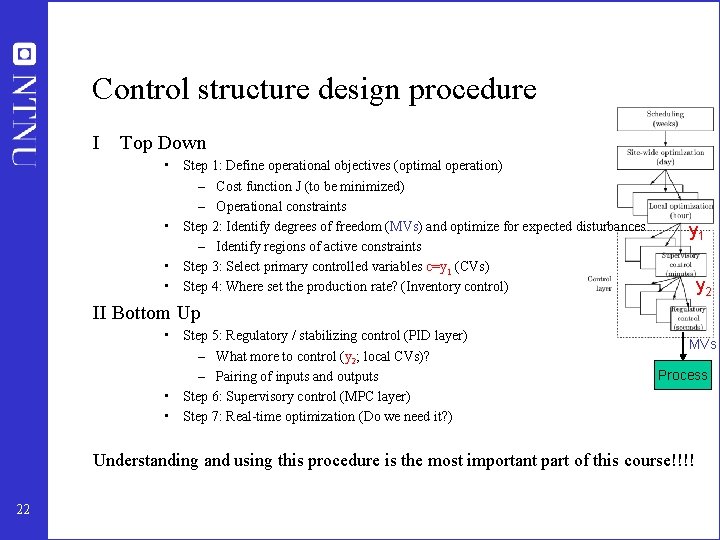
Control structure design procedure I Top Down • Step 1: Define operational objectives (optimal operation) – Cost function J (to be minimized) – Operational constraints • Step 2: Identify degrees of freedom (MVs) and optimize for expected disturbances – Identify regions of active constraints • Step 3: Select primary controlled variables c=y 1 (CVs) • Step 4: Where set the production rate? (Inventory control) y 1 y 2 II Bottom Up • Step 5: Regulatory / stabilizing control (PID layer) – What more to control (y 2; local CVs)? – Pairing of inputs and outputs • Step 6: Supervisory control (MPC layer) • Step 7: Real-time optimization (Do we need it? ) MVs Process Understanding and using this procedure is the most important part of this course!!!! 22

Step 1. Define optimal operation (economics) • • What are we going to use our degrees of freedom u (MVs) for? Define scalar cost function J(u, x, d) – u: degrees of freedom (usually steady-state) – d: disturbances – x: states (internal variables) Typical cost function: J = cost feed + cost energy – value products • Optimize operation with respect to u for given d (usually steady-state): minu J(u, x, d) subject to: Model equations: f(u, x, d) = 0 Operational constraints: g(u, x, d) < 0 23

Optimal operation distillation column • • Distillation at steady state with given p and F: N=2 DOFs, e. g. L and V Cost to be minimized (economics) cost energy (heating+ cooling) J = - P where P= p. D D + p. B B – p. F F – p. V V value products 24 cost feed • Constraints Purity D: For example x. D, impurity · max Purity B: For example, x. B, impurity · max Flow constraints: min · D, B, L etc. · max Column capacity (flooding): V · Vmax, etc. Pressure: 1) p given, 2) p free: pmin · pmax Feed: 1) F given 2) F free: F · Fmax • Optimal operation: Minimize J with respect to steady-state DOFs

Optimal operation minimize J = cost feed + cost energy – value products Two main cases (modes) depending on marked conditions: 1. Given feed Amount of products is then usually indirectly given and J = cost energy. Optimal operation is then usually unconstrained: “maximize efficiency (energy)” 2. Feed free Control: Operate at optimal tradeoff (not obvious what to control to achieve this) Products usually much more valuable than feed + energy costs small. Optimal operation is then usually constrained: 25 “maximize production” Control: Operate at bottleneck (“obvious what to control”)

Comments optimal operation • Do not forget to include feedrate as a degree of freedom!! – For LNG plant it may be optimal to have max. compressor power or max. compressor speed, and adjust feedrate of LNG – For paper machine it may be optimal to have max. drying and adjust the feedrate of paper (speed of the paper machine) to meet spec! • Control at bottleneck – see later: “Where to set the production rate” 26

Step 2: (a) Identify degrees of freedom and (b) optimize for expected disturbances • Optimization: Identify regions of active constraints • Time consuming! Control 3 active constraints 1 2 3 27 2 1 3 unconstrained degrees of freedom -> Find 3 CVs

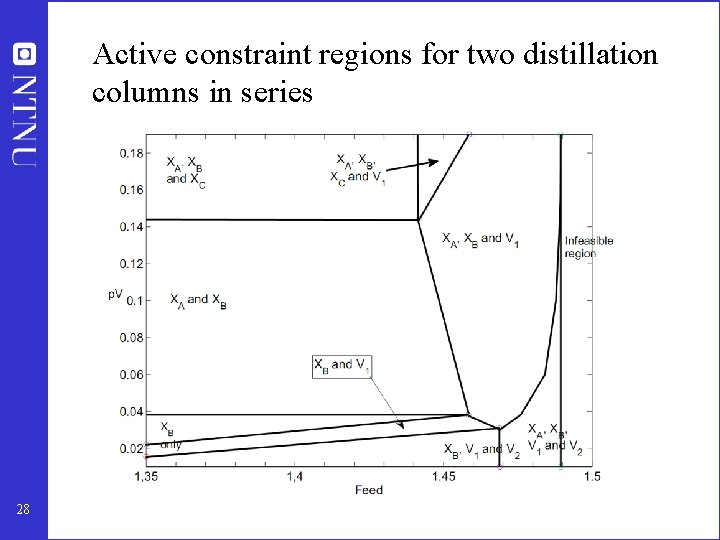
Active constraint regions for two distillation columns in series 28

Step 2 a: Degrees of freedom (DOFs) for operation NOT as simple as one may think! To find all operational (dynamic) degrees of freedom: • Count valves! (Nvalves) • “Valves” also includes adjustable compressor power, etc. Anything we can manipulate! BUT: not all these have a (steady-state) effect on the economics 29

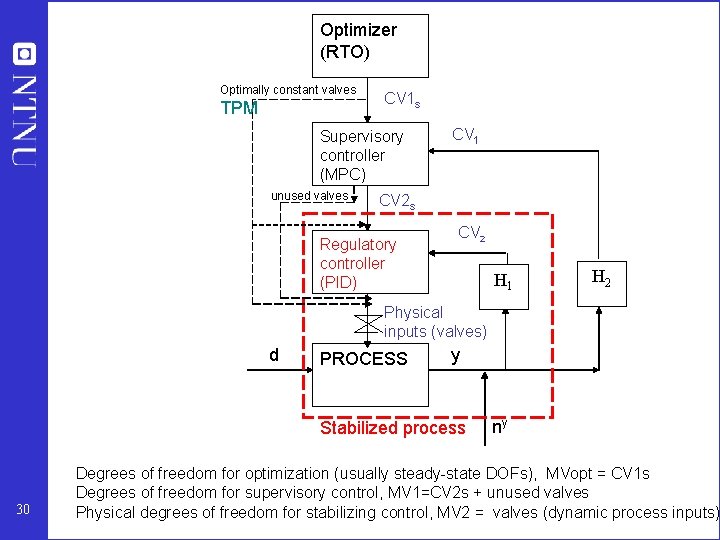
Optimizer (RTO) Optimally constant valves TPM CV 1 s Supervisory controller (MPC) unused valves CV 1 CV 2 s Regulatory controller (PID) CV 2 H 1 H 2 Physical inputs (valves) d PROCESS y Stabilized process 30 ny Degrees of freedom for optimization (usually steady-state DOFs), MVopt = CV 1 s Degrees of freedom for supervisory control, MV 1=CV 2 s + unused valves Physical degrees of freedom for stabilizing control, MV 2 = valves (dynamic process inputs)

Steady-state degrees of freedom (DOFs) IMPORTANT! DETERMINES THE NUMBER OF VARIABLES TO CONTROL! • No. of primary CVs = No. of steady-state DOFs Methods to obtain no. of steady-state degrees of freedom (Nss): 1. Equation-counting • • Nss = no. of variables – no. of equations/specifications Very difficult in practice 2. Valve-counting (easier!) • • Nss = Nvalves – N 0 ss – Nspecs N 0 ss = variables with no steady-state effect 3. Potential number for some units (useful for checking!) 4. Correct answer: Will eventually it when we perform optimization 31 CV = controlled variable (c)

Steady-state degrees of freedom (Nss): 2. Valve-counting • Nvalves = no. of dynamic (control) DOFs (valves) • Nss = Nvalves – N 0 ss – Nspecs : no. of steady-state DOFs • N 0 ss = N 0 y + N 0, valves : no. of variables with no steady-state effect – N 0, valves : no. purely dynamic control DOFs – N 0 y : no. controlled variables (liquid levels) with no steady-state effect • Nspecs: No of equality specifications (e. g. , given pressure) 32

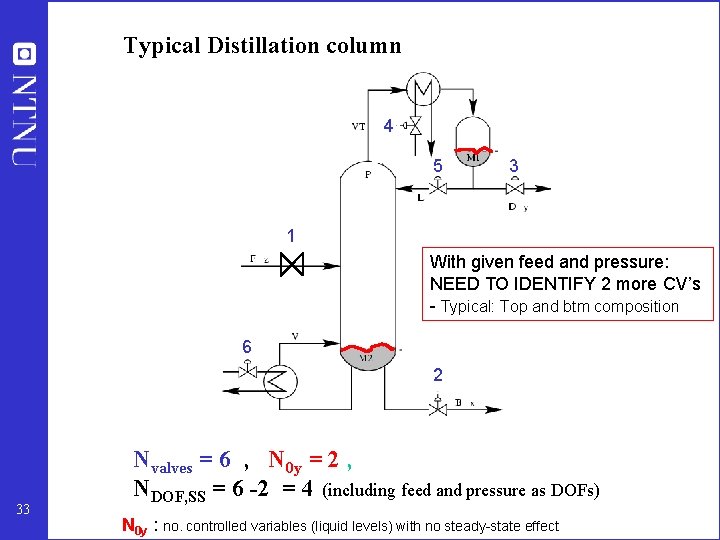
Typical Distillation column 4 5 3 1 With given feed and pressure: NEED TO IDENTIFY 2 more CV’s - Typical: Top and btm composition 6 2 33 Nvalves = 6 , N 0 y = 2 , NDOF, SS = 6 -2 = 4 (including feed and pressure as DOFs) N 0 y : no. controlled variables (liquid levels) with no steady-state effect

Heat-integrated distillation process 34

Heat-integrated distillation process 35

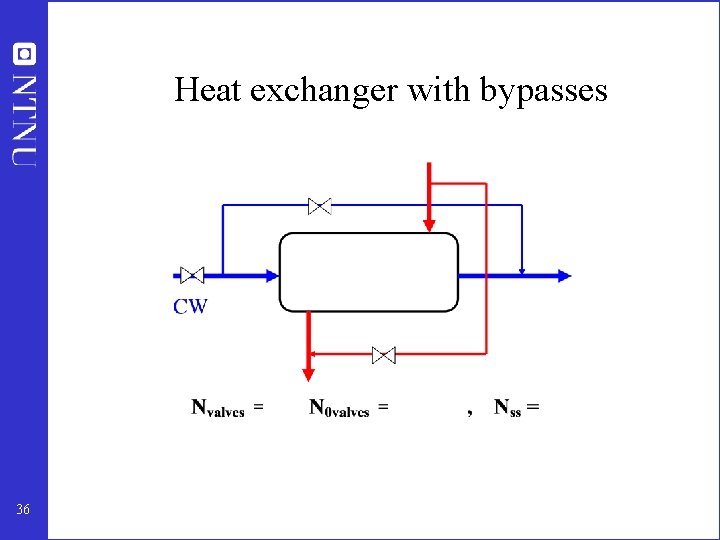
Heat exchanger with bypasses 36

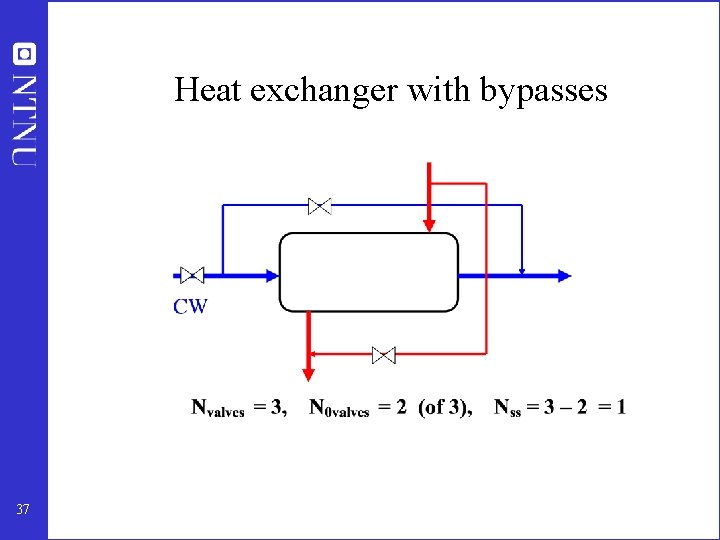
Heat exchanger with bypasses 37

Steady-state degrees of freedom (Nss): 3. Potential number for some process units • • • 38 • • each external feedstream: 1 (feedrate) splitter: n-1 (split fractions) where n is the number of exit streams mixer: 0 compressor, turbine, pump: 1 (work/speed) adiabatic flash tank: 0* liquid phase reactor: 1 (holdup reactant) gas phase reactor: 0* heat exchanger: 1 (bypass or flow) column (e. g. distillation) excluding heat exchangers: 0* + no. of sidestreams pressure* : add 1 DOF at each extra place you set pressure (using an extra valve, compressor or pump), e. g. in adiabatic flash tank, gas phase reactor or absorption column *Pressure is normally assumed to be given by the surrounding process and is then not a degree of freedom Ref: Araujo, Govatsmark and Skogestad (2007) Extension to closed cycles: Jensen and Skogestad (2009) Real number may be less, for example, if there is no bypass valve

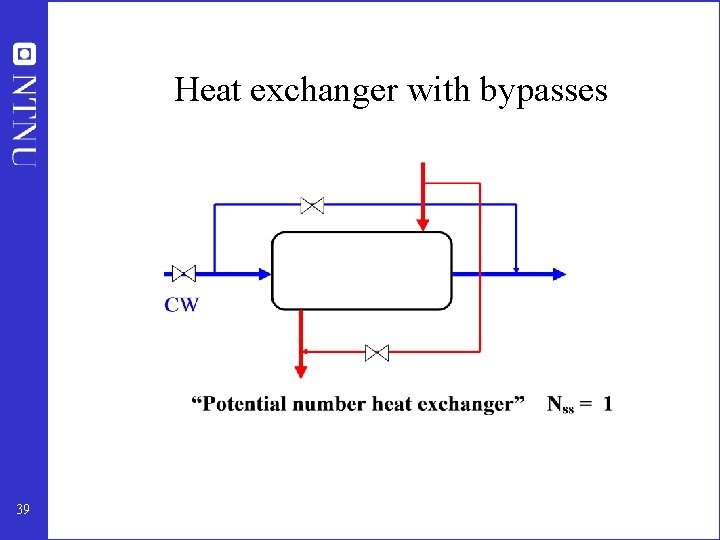
Heat exchanger with bypasses 39

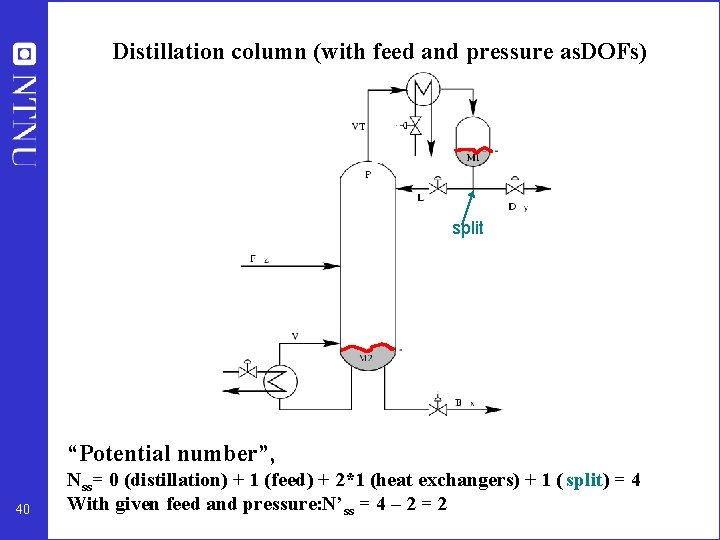
Distillation column (with feed and pressure as. DOFs) split “Potential number”, 40 Nss= 0 (distillation) + 1 (feed) + 2*1 (heat exchangers) + 1 ( split) = 4 With given feed and pressure: N’ ss = 4 – 2 = 2

Heat-integrated distillation process 41

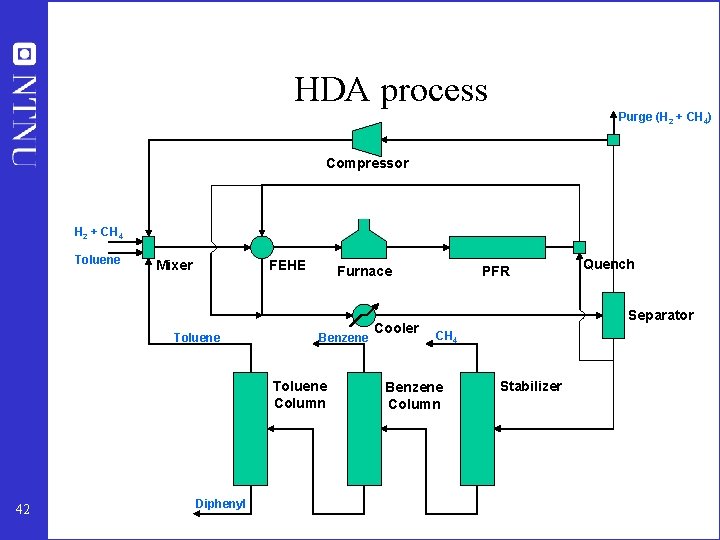
HDA process Purge (H 2 + CH 4) Compressor H 2 + CH 4 Toluene Mixer FEHE Toluene Furnace Benzene Toluene Column 42 Diphenyl Cooler PFR Quench Separator CH 4 Benzene Column Stabilizer

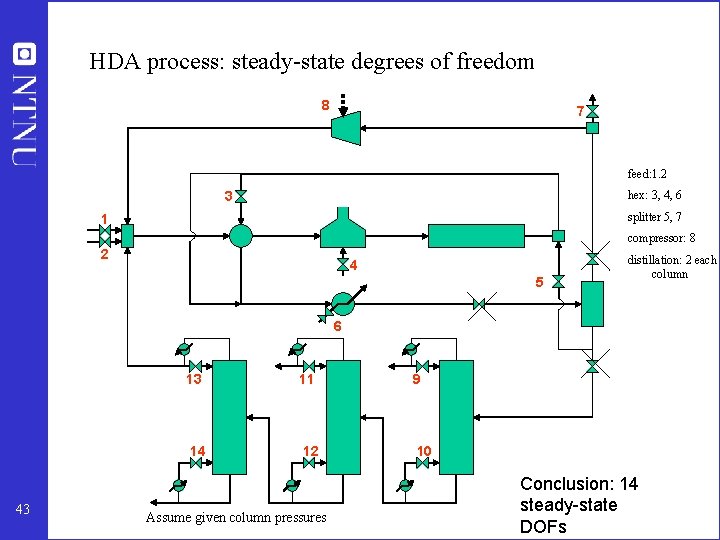
HDA process: steady-state degrees of freedom 8 7 feed: 1. 2 3 hex: 3, 4, 6 splitter 5, 7 1 compressor: 8 2 4 5 distillation: 2 each column 6 43 13 11 9 14 12 10 Assume given column pressures Conclusion: 14 steady-state DOFs

• Check that there are enough manipulated variables (DOFs) - both dynamically and at steady-state (step 2) • Otherwise: Need to add equipment – extra heat exchanger – bypass – surge tank 44

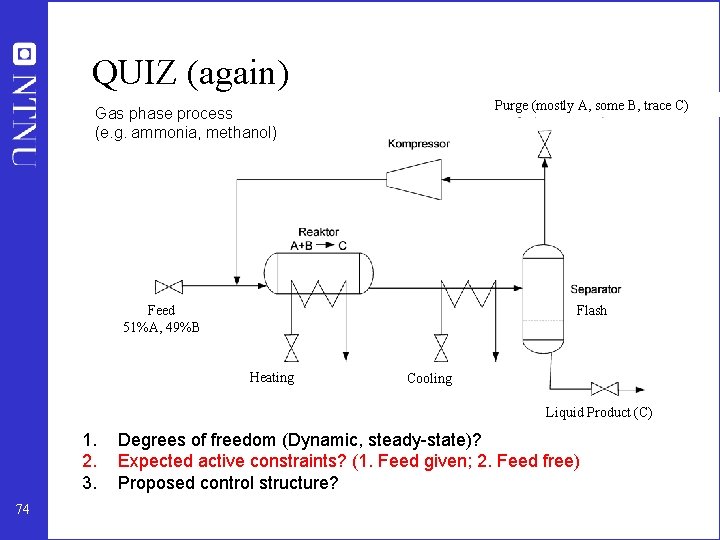
QUIZ Purge (mostly A, some B, trace C) Gas phase process (e. g. ammonia, methanol) Feed 51%A, 49%B Flash Heating Cooling Liquid Product (C) 1. 2. 3. 45 Degrees of freedom (Dynamic, steady-state)? Expected active constraints? Proposed control structure?

Step 3: Implementation of optimal operation • Optimal operation for given d*: minu J(u, x, d) subject to: Model equations: Operational constraints: → uopt(d*) f(u, x, d) = 0 g(u, x, d) < 0 Problem: Usally cannot keep uopt constant because disturbances d change 46 How should we adjust the degrees of freedom (u)? What should we control?

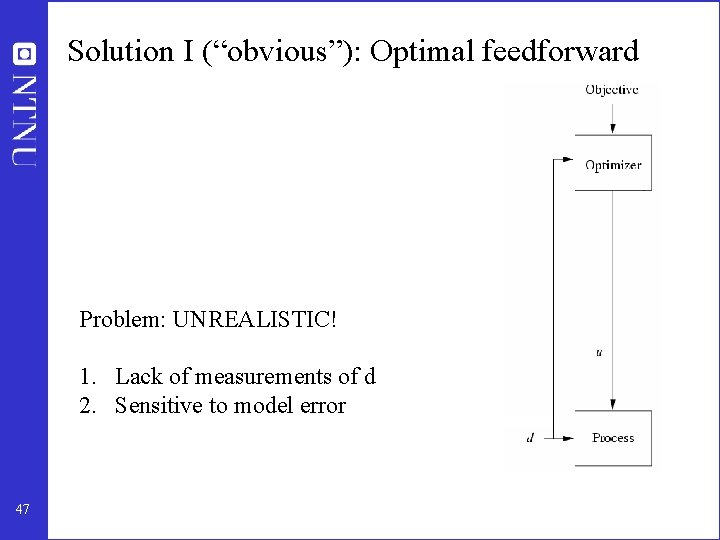
Solution I (“obvious”): Optimal feedforward Problem: UNREALISTIC! 1. Lack of measurements of d 2. Sensitive to model error 47

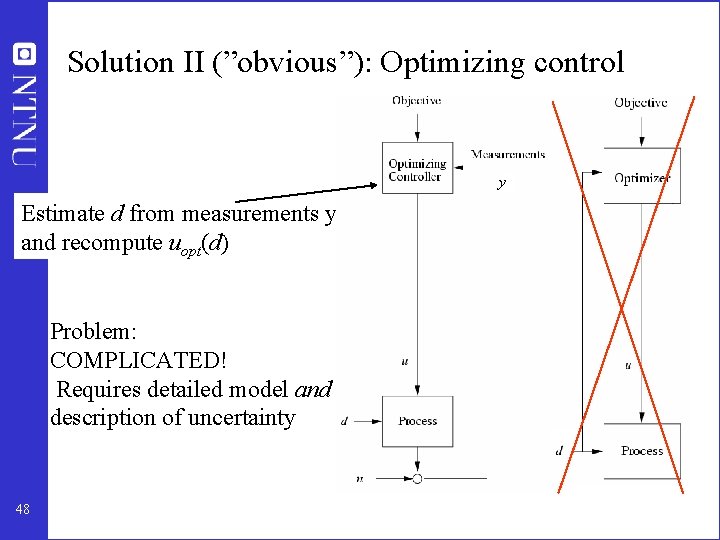
Solution II (”obvious”): Optimizing control y Estimate d from measurements y and recompute uopt(d) Problem: COMPLICATED! Requires detailed model and description of uncertainty 48

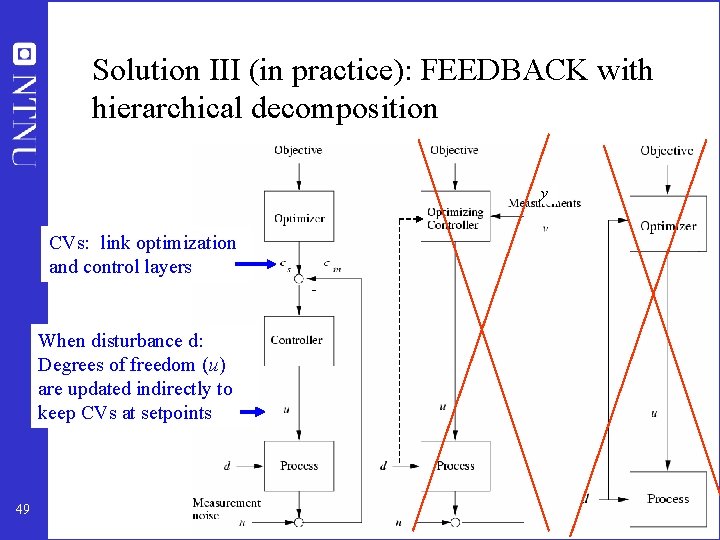
Solution III (in practice): FEEDBACK with hierarchical decomposition y CVs: link optimization and control layers When disturbance d: Degrees of freedom (u) are updated indirectly to keep CVs at setpoints 49

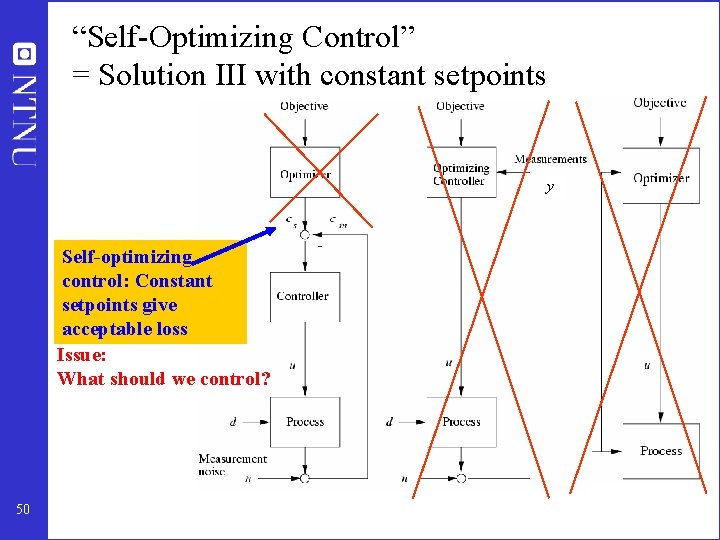
“Self-Optimizing Control” = Solution III with constant setpoints y Self-optimizing control: Constant setpoints give acceptable loss Issue: What should we control? 50

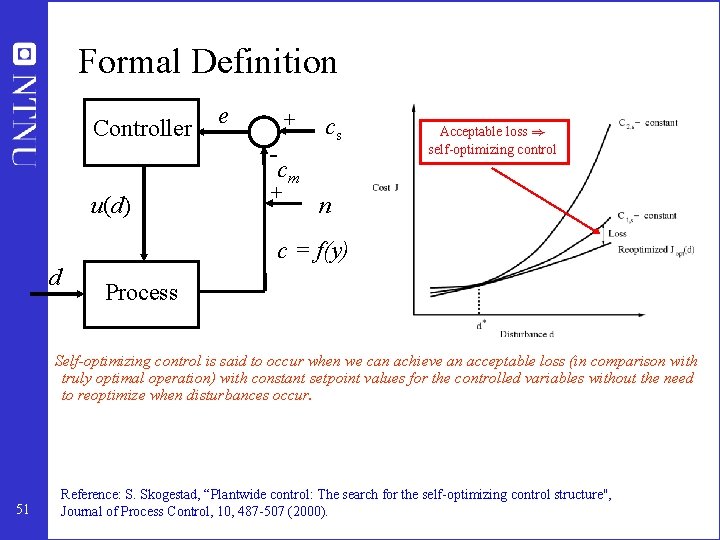
Formal Definition Controller e + - cs cm u(d) + Acceptable loss ) self-optimizing control n c = f(y) d Process Self-optimizing control is said to occur when we can achieve an acceptable loss (in comparison with truly optimal operation) with constant setpoint values for the controlled variables without the need to reoptimize when disturbances occur. 51 Reference: S. Skogestad, “Plantwide control: The search for the self-optimizing control structure'', Journal of Process Control, 10, 487 -507 (2000).

How does self-optimizing control (solution III) work? • • • When disturbances d occur, controlled variable c deviates from setpoint cs Feedback controller changes degree of freedom u to u. FB(d) to keep c at cs Near-optimal operation / acceptable loss (self-optimizing control) is achieved if – u. FB(d) ≈ uopt(d) – or more generally, J(u. FB(d)) ≈ J(uopt(d)) 52 • Of course, variation of u. FB(d) is different for different CVs c. • We need to look for variables, for which J(u. FB(d)) ≈ J(uopt(d)) or Loss = J(u. FB(d)) J(uopt(d)) is small

Remarks “self-optimizing control” 1. Old idea (Morari et al. , 1980): “We want to find a function c of the process variables which when held constant, leads automatically to the optimal adjustments of the manipulated variables, and with it, the optimal operating conditions. ” 2. “Self-optimizing control” = acceptable steady-state behavior (loss) with constant CVs. is similar to “Self-regulation” = acceptable dynamic behavior with constant MVs. 3. The ideal self-optimizing variable c is the gradient (c = J/ u = Ju) 53 – Keep gradient at zero for all disturbances (c = Ju=0) – Problem: no measurement of gradient

Step 3. What should we control (c)? Simple examples What should we control? 54

Optimal operation - Runner Optimal operation of runner – Cost to be minimized, J=T – One degree of freedom (u=power) – What should we control? 55

Optimal operation - Runner Self-optimizing control: Sprinter (100 m) • 1. Optimal operation of Sprinter, J=T – Active constraint control: • Maximum speed (”no thinking required”) 56

Optimal operation - Runner Self-optimizing control: Marathon (40 km) • 2. Optimal operation of Marathon runner, J=T 57

Optimal operation - Runner Solution 1 Marathon: Optimizing control • Even getting a reasonable model requires > 10 Ph. D’s … and the model has to be fitted to each individual…. • Clearly impractical! 58

Optimal operation - Runner Solution 2 Marathon – Feedback (Self-optimizing control) – What should we control? 59

Optimal operation - Runner Self-optimizing control: Marathon (40 km) • Optimal operation of Marathon runner, J=T • Any self-optimizing variable c (to control at constant setpoint)? • • 60 c 1 = distance to leader of race c 2 = speed c 3 = heart rate c 4 = level of lactate in muscles

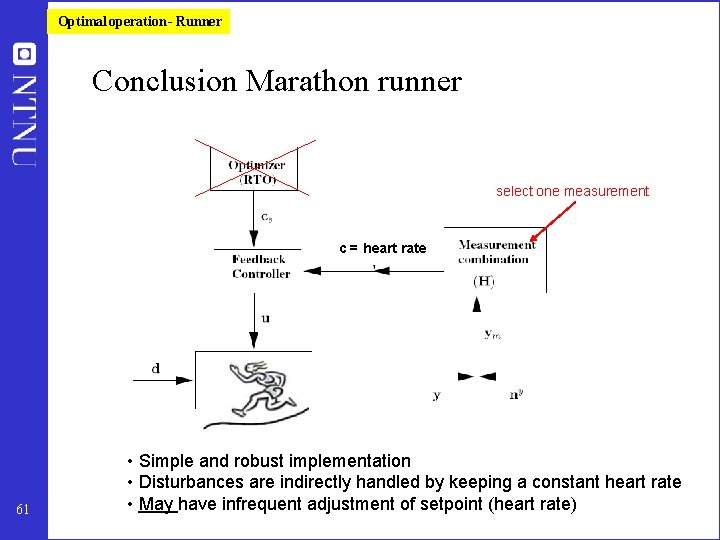
Optimal operation - Runner Conclusion Marathon runner select one measurement c = heart rate 61 • Simple and robust implementation • Disturbances are indirectly handled by keeping a constant heart rate • May have infrequent adjustment of setpoint (heart rate)

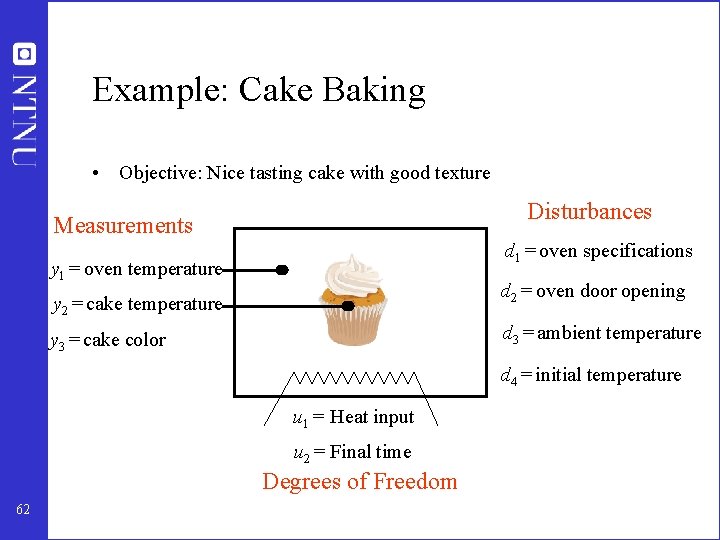
Example: Cake Baking • Objective: Nice tasting cake with good texture Disturbances Measurements d 1 = oven specifications y 1 = oven temperature d 2 = oven door opening y 2 = cake temperature d 3 = ambient temperature y 3 = cake color d 4 = initial temperature u 1 = Heat input u 2 = Final time Degrees of Freedom 62

Further examples self-optimizing control • • Marathon runner Central bank Cake baking Business systems (KPIs) Investment portifolio Biology Chemical process plants: Optimal blending of gasoline Define optimal operation (J) and look for ”magic” variable (c) which when kept constant gives acceptable loss (selfoptimizing control) 63

More on further examples • • • Central bank. J = welfare. u = interest rate. c=inflation rate (2. 5%) Cake baking. J = nice taste, u = heat input. c = Temperature (200 C) Business, J = profit. c = ”Key performance indicator (KPI), e. g. – Response time to order – Energy consumption pr. kg or unit – Number of employees – Research spending Optimal values obtained by ”benchmarking” • • Investment (portofolio management). J = profit. c = Fraction of investment in shares (50%) Biological systems: – ”Self-optimizing” controlled variables c have been found by natural selection – Need to do ”reverse engineering” : • • 64 Find the controlled variables used in nature From this possibly identify what overall objective J the biological system has been attempting to optimize

Summary Step 3. What should we control (c)? c=Hy y – available measurements (including u’s) H – selection of combination matrix What should we control? Equivalently: What should H be? 1. Control active constraints! 2. Unconstrained variables: Control self-optimizing variables! 65

1. CONTROL ACTIVE CONSTRAINTS! 66

Example: Optimal operation distillation • Cost to be minimized (economics) cost energy (heating+ cooling) J = - P where P= p. D D + p. B B – p. F F – p. V V value products cost feed • Constraints Purity D: For example Purity B: For example, Flow constraints: Column capacity (flooding): 67 x. D, impurity · max x. B, impurity · max 0 · D, B, L etc. · max V · Vmax, etc.

Expected active constraints distillation 1. Valuable product: Purity spec. always active (if we get paid for impurity) – Reason: Amount of valuable product (D or B) should always be maximized • Avoid product “give-away” (“Sell water as methanol”) • Also saves energy • valuable product methanol + max. 5% water Control implications valuable product: Control purityat spec. 2. “Cheap” product. May want to over-purify! Trade-off: – Yes, increased recovery of valuable product (less loss) – No, costs energy May give unconstrained optimum 68 methanol + water cheap product (byproduct) water + max. 2% methanol

Active constraint regions distillation • No pay for impurity (p. D=x*PD 0): Can have no active constraints p. V x. Dmax, x. Bmax (0) x. Dmax (1) Region below here does not exist if p. D is constant (“expensive product purity constraint x. Dmax always active”) p. V=0 No constraints. Overpurify D and B (2) Vmax, (1) Vmax, x. Dmax (0) Infeas. x. Dmax x. Bmax, Vmax (-1) F 69

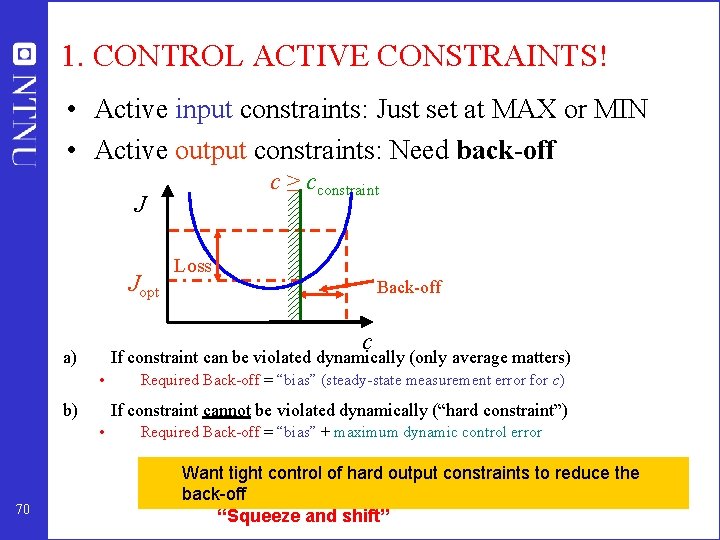
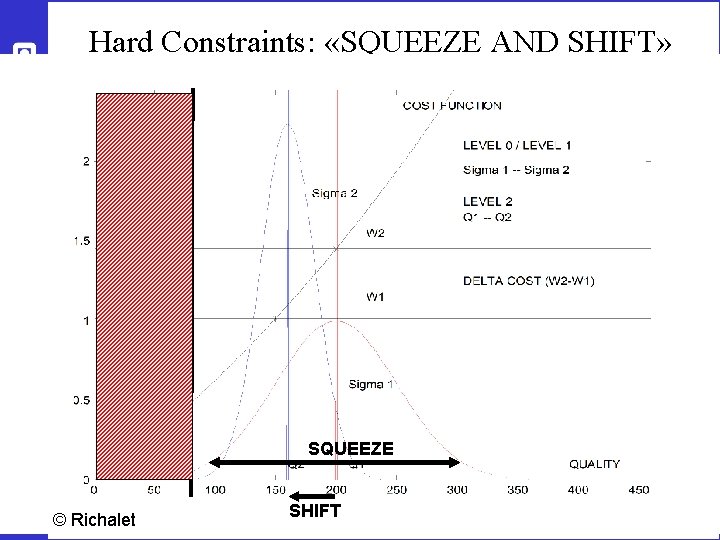
1. CONTROL ACTIVE CONSTRAINTS! • Active input constraints: Just set at MAX or MIN • Active output constraints: Need back-off c ≥ cconstraint J Jopt Back-off c a) If constraint can be violated dynamically (only average matters) • b) Required Back-off = “bias” (steady-state measurement error for c) If constraint cannot be violated dynamically (“hard constraint”) • 70 Loss Required Back-off = “bias” + maximum dynamic control error Want tight control of hard output constraints to reduce the back-off “Squeeze and shift”

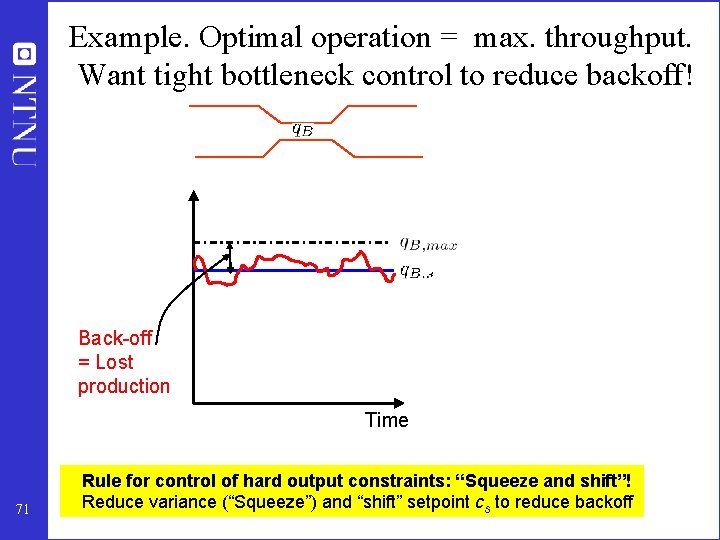
Example. Optimal operation = max. throughput. Want tight bottleneck control to reduce backoff! Back-off = Lost production Time 71 Rule for control of hard output constraints: “Squeeze and shift”! Reduce variance (“Squeeze”) and “shift” setpoint cs to reduce backoff

Hard Constraints: «SQUEEZE AND SHIFT» SQUEEZE 72 © Richalet SHIFT

• SUMMARY ACTIVE CONSTRAINTS – cconstraint = value of active constraint – Implementation of active constraints is usually “obvious”, but may need “back-off” (safety limit) for hard output constraints • Cs = Cconstraint - backoff – Want tight control of hard output constraints to reduce the back-off • “Squeeze and shift” 73

QUIZ (again) Purge (mostly A, some B, trace C) Gas phase process (e. g. ammonia, methanol) Feed 51%A, 49%B Flash Heating Cooling Liquid Product (C) 1. 2. 3. 74 Degrees of freedom (Dynamic, steady-state)? Expected active constraints? (1. Feed given; 2. Feed free) Proposed control structure?

2. UNCONSTRAINED VARIABLES: - WHAT MORE SHOULD WE CONTROL? - WHAT ARE GOOD “SELF-OPTIMIZING” VARIABLES? • Intuition: “Dominant variables” (Shinnar) • Is there any systematic procedure? A. Sensitive variables: “Max. gain rule” (Gain= Minimum singular value) B. “Brute force” loss evaluation C. Optimal linear combination of measurements, c = Hy 75