PLANTWIDE CONTROL Sigurd Skogestad Department of Chemical Engineering

PLANTWIDE CONTROL Sigurd Skogestad Department of Chemical Engineering Norwegian University of Science and Tecnology (NTNU) Trondheim, Norway Sept. 2005 1

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (primary CV’s) (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control (secondary CV’s) ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 2

Idealized view of control (“Ph. D. control”) 3

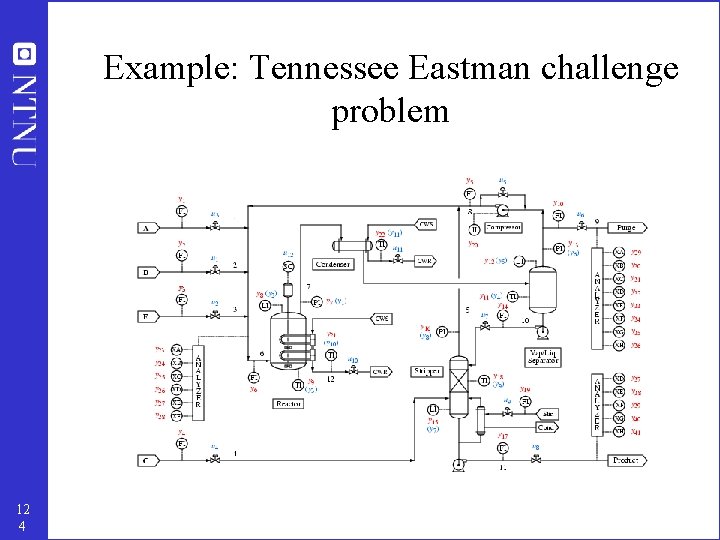
Practice: Tennessee Eastman challenge problem (Downs, 1991) (“PID control”) 4

How we design a control system for a complete chemical plant? • • 5 Where do we start? What should we control? and why? etc.

Idealized view II: Optimizing control 6

Practice II: Hierarchical decomposition with separate layers What should we control? 7

• Alan Foss (“Critique of chemical process control theory”, AICh. E Journal, 1973): The central issue to be resolved. . . is the determination of control system structure. Which variables should be measured, which inputs should be manipulated and which links should be made between the two sets? There is more than a suspicion that the work of a genius is needed here, for without it the control configuration problem will likely remain in a primitive, hazily stated and wholly unmanageable form. The gap is present indeed, but contrary to the views of many, it is theoretician who must close it. • Carl Nett (1989): Minimize control system complexity subject to the achievement of accuracy specifications in the face of uncertainty. 8

Control structure design • Not the tuning and behavior of each control loop, • But rather the control philosophy of the overall plant with emphasis on the structural decisions: – – Selection of controlled variables (“outputs”) Selection of manipulated variables (“inputs”) Selection of (extra) measurements Selection of control configuration (structure of overall controller that interconnects the controlled, manipulated and measured variables) – Selection of controller type (LQG, H-infinity, PID, decoupler, MPC etc. ). • That is: Control structure design includes all the decisions we need make to get from ``PID control’’ to “Ph. D” control 9

Process control: “Plantwide control” = “Control structure design for complete chemical plant” • • Large systems Each plant usually different – modeling expensive Slow processes – no problem with computation time Structural issues important – What to control? – Extra measurements – Pairing of loops 10

Previous work on plantwide control • Page Buckley (1964) - Chapter on “Overall process control” (still industrial practice) • Greg Shinskey (1967) – process control systems • Alan Foss (1973) - control system structure • Bill Luyben et al. (1975 - ) – case studies ; “snowball effect” • George Stephanopoulos and Manfred Morari (1980) – synthesis of control structures for chemical processes • Ruel Shinnar (1981 - ) - “dominant variables” • Jim Downs (1991) - Tennessee Eastman challenge problem • Larsson and Skogestad (2000): Review of plantwide control 11

• Control structure selection issues are identified as important also in other industries. Professor Gary Balas (Minnesota) at ECC’ 03 about flight control at Boeing: The most important control issue has always been to select the right controlled variables --- no systematic tools used! 12

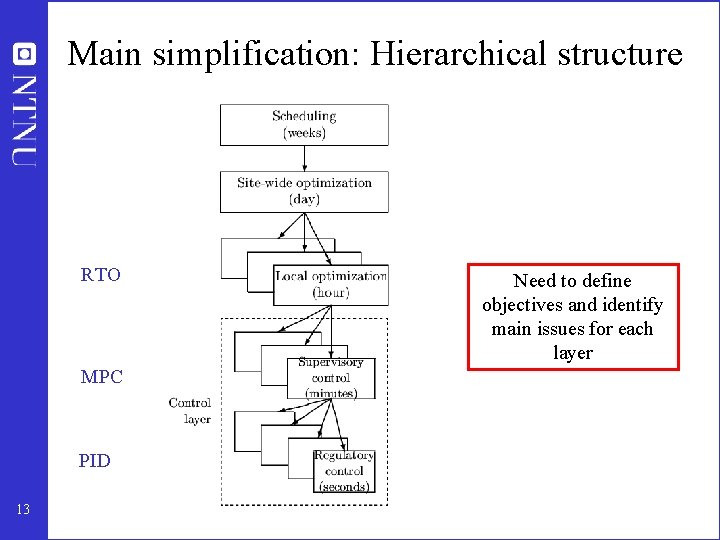
Main simplification: Hierarchical structure RTO MPC PID 13 Need to define objectives and identify main issues for each layer

Regulatory control (seconds) • Purpose: “Stabilize” the plant by controlling selected ‘’secondary’’ variables (y 2) such that the plant does not drift too far away from its desired operation • Use simple single-loop PI(D) controllers • Status: Many loops poorly tuned – Most common setting: Kc=1, I=1 min (default) – Even wrong sign of gain Kc …. 14

Regulatory control……. . . • Trend: Can do better! Carefully go through plant and retune important loops using standardized tuning procedure • Exists many tuning rules, including Skogestad (SIMC) rules: – Kc = (1/k) ( 1/ [ c + ]) I = min ( 1, 4[ c + ]), Typical: c= – “Probably the best simple PID tuning rules in the world” © Carlsberg • Outstanding structural issue: What loops to close, that is, which variables (y 2) to control? 15

Supervisory control (minutes) • Purpose: Keep primary controlled variables (c=y 1) at desired values, using as degrees of freedom the setpoints y 2 s for the regulatory layer. • Status: Many different “advanced” controllers, including feedforward, decouplers, overrides, cascades, selectors, Smith Predictors, etc. • Issues: – Which variables to control may change due to change of “active constraints” – Interactions and “pairing” 16

Supervisory control…. . . • Trend: Model predictive control (MPC) used as unifying tool. – Linear multivariable models with input constraints – Tuning (modelling) is time-consuming and expensive • Issue: When use MPC and when use simpler single-loop decentralized controllers ? – MPC is preferred if active constraints (“bottleneck”) change. – Avoids logic for reconfiguration of loops • Outstanding structural issue: – What primary variables c=y 1 to control? 17

Local optimization (hour) • Purpose: Minimize cost function J and: – Identify active constraints – Recompute optimal setpoints y 1 s for the controlled variables • Status: Done manually by clever operators and engineers • Trend: Real-time optimization (RTO) based on detailed nonlinear steady-state model • Issues: – Optimization not reliable. – Need nonlinear steady-state model – Modelling is time-consuming and expensive 18

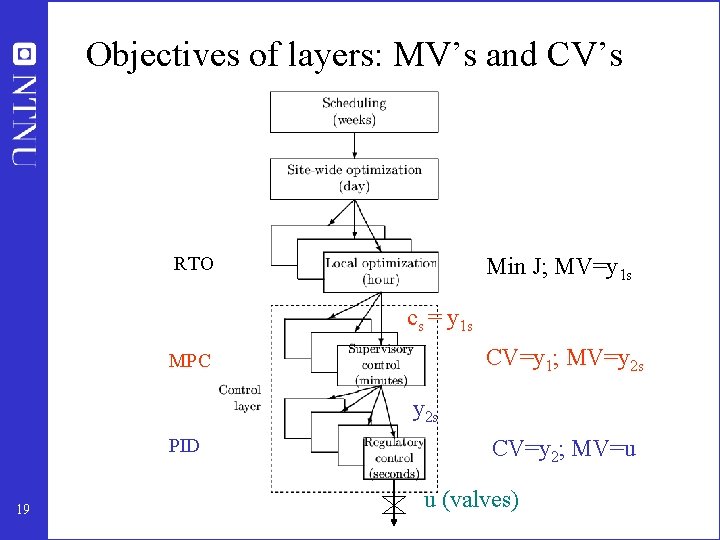
Objectives of layers: MV’s and CV’s RTO Min J; MV=y 1 s cs = y 1 s CV=y 1; MV=y 2 s MPC y 2 s PID 19 CV=y 2; MV=u u (valves)

Stepwise procedure plantwide control I. TOP-DOWN Step 1. DEGREES OF FREEDOM Step 2. OPERATIONAL OBJECTIVES Step 3. WHAT TO CONTROL? (primary CV’s c=y 1) Step 4. PRODUCTION RATE II. BOTTOM-UP (structure control system): Step 5. REGULATORY CONTROL LAYER (PID) “Stabilization” What more to control? (secondary CV’s y 2) Step 6. SUPERVISORY CONTROL LAYER (MPC) Decentralization Step 7. OPTIMIZATION LAYER (RTO) Can we do without it? 20

Outline • About Trondheim and myself • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimzing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 21

Step 1. Degrees of freedom (DOFs) • m – dynamic (control) degrees of freedom = valves • u 0 – steady-state degrees of freedom • Nm : no. of dynamic (control) DOFs (valves) • Nu 0 = Nm- N 0 : no. of steady-state DOFs – N 0 = N 0 y + N 0 m : no. of variables with no steady-state effect • N 0 m : no. purely dynamic control DOFs • N 0 y : no. controlled variables (liquid levels) with no steady-state effect • Cost J depends normally on steady-state DOFs 22

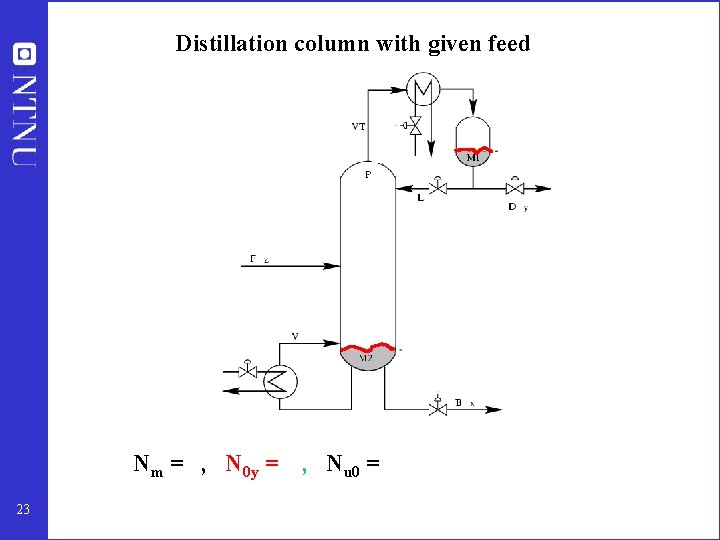
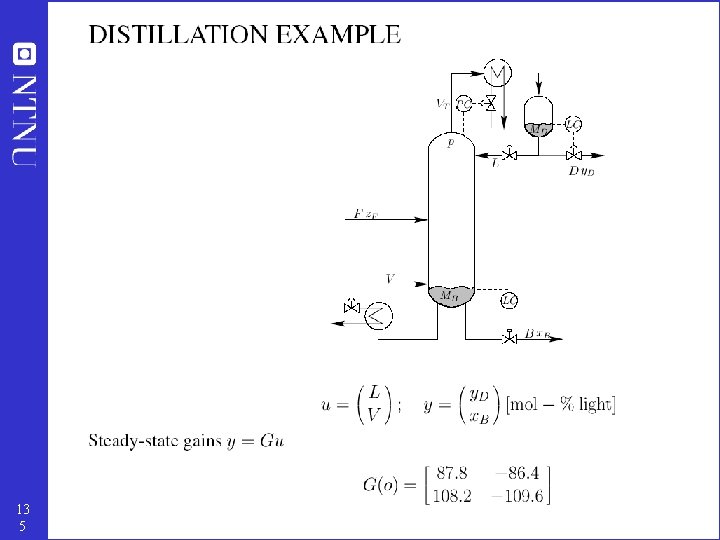
Distillation column with given feed Nm = , N 0 y = 23 , Nu 0 =

Heat-integrated distillation process 24

Heat exchanger with bypasses 25

Typical number of steady-state degrees of freedom (u 0) for some process units • • • 26 each external feedstream: 1 (feedrate) splitter: n-1 (split fractions) where n is the number of exit streams mixer: 0 compressor, turbine, pump: 1 (work) adiabatic flash tank: 1 (0 with “given” pressure) liquid phase reactor: 1 (volume) gas phase reactor: 1 (0 with “given” pressure) heat exchanger: 1 (duty or net area) distillation column excluding heat exchangers: 1 (0 with “given” pressure) + number of sidestreams Comment “given” pressure: Either (1) pressure is fixed, or (2) there is no MV (valve) for setting the pressure in the unit, so it is “given” by the surrounding process

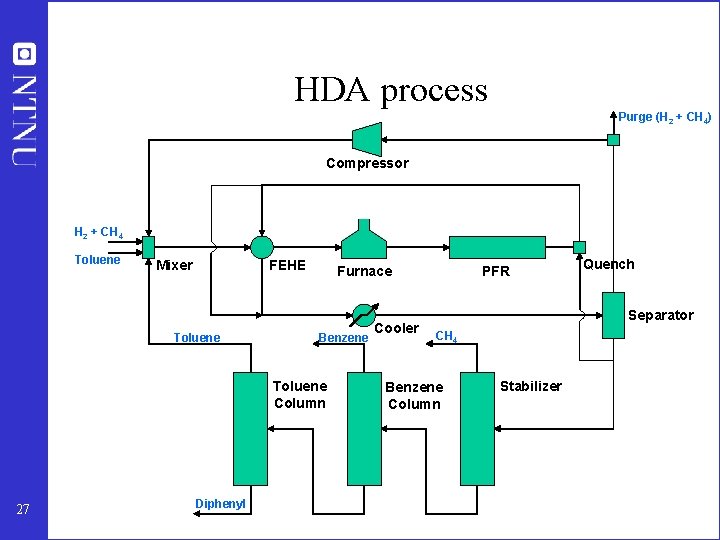
HDA process Purge (H 2 + CH 4) Compressor H 2 + CH 4 Toluene Mixer FEHE Toluene Furnace Benzene Toluene Column 27 Diphenyl Cooler PFR Quench Separator CH 4 Benzene Column Stabilizer

• Check that there are enough manipulated variables (DOFs) - both dynamically and at steady-state (step 2) • Otherwise: Need to add equipment – extra heat exchanger – bypass – surge tank 28

Outline • About Trondheim and myself • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimzing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 29

Optimal operation (economics) • • What are we going to use our degrees of freedom for? Define scalar cost function J(u 0, x, d) – u 0: degrees of freedom – d: disturbances – x: states (internal variables) Typical cost function: J = cost feed + cost energy – value products • Optimal operation for given d: minu 0 J(u 0, x, d) subject to: Model equations: f(u 0, x, d) = 0 Operational constraints: g(u 0, x, d) < 0 30

Optimal operation distillation column • • Steady-state DOFs (given p and F): 2, for example L/D and V Cost to be minimized (economics) cost energy (heating+ cooling) J = - P where P= p. D D + p. B B – p. F F – p. V V • value products cost feed Constraints Purity D: For example Purity B: For example, Flow constraints: Column capacity (flooding): Pressure: 1) p given, Feed: 1) F given • 31 x. D, impurity · max x. B, impurity · max min · D, B, L etc. · max V · Vmax, etc. 2) p free: pmin · pmax 2) F free: F · Fmax Optimal operation: Minimize J with respect to steady-state DOFs

Outline • About Trondheim and myself • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 32

Step 3. What should we control (c)? Outline • Implementation of optimal operation • Self-optimizing control • Uncertainty (d and n) • Example: Marathon runner • Methods for finding the “magic” self-optimizing variables: A. Large gain: Minimum singular value rule B. “Brute force” loss evaluation C. Optimal combination of measurements • Example: Recycle process • Summary 33

Implementation of optimal operation • Optimal operation for given d*: minu 0 J(u 0, x, d) subject to: Model equations: Operational constraints: → u 0 opt(d*) f(u 0, x, d) = 0 g(u 0, x, d) < 0 Problem: Cannot keep u 0 opt constant because disturbances d change 34 Distillation: Steady-state degrees of freedom u 0 could be L/D and V. Cannot keep these constant

Implementation of optimal operation (Cannot keep u 0 opt constant) ”Obvious” solution: Optimizing control Estimate d from measurements and recompute u 0 opt(d) Problem: Too complicated (requires detailed model and description of uncertainty) 35

Implementation of optimal operation (Cannot keep u 0 opt constant) Simpler solution: Look for another variable c which is better to keep constant Note: u 0 will indirectly change when d changes and control c at constant setpoint cs = copt(d*) 36

What c’s should we control? • Optimal solution is usually at constraints, that is, most of the degrees of freedom are used to satisfy “active constraints”, g(u 0, d) = 0 • CONTROL ACTIVE CONSTRAINTS! – cs = value of active constraint – Implementation of active constraints is usually simple. • WHAT MORE SHOULD WE CONTROL? – Find variables c for remaining unconstrained degrees of freedom u. 37

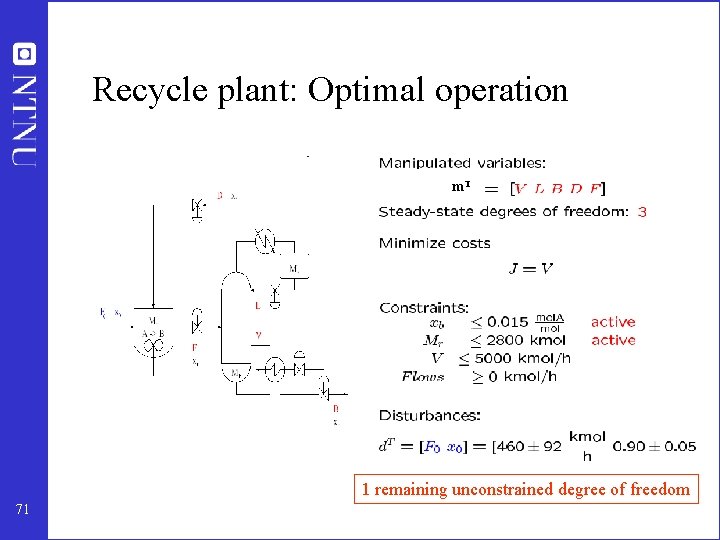
Solution to optimal operation distillation • Cost to be minimized J = - P where P= p. D D + p. B B – p. F F – p. V V • • Optimal operation: Minimize J with respect to DOFs General: Optimal solution with N DOFs: – – • N – Nu DOFs used to satisfy “active” constraints (· is =) Nu remaining unconstrained variables Usually: Nu zero or small Distillation at steady state with given p and F: • N=2 DOFs. Three cases: 1. 2. 3. Nu=0: Two active constraints (for example, x. D, impurity = max. x. B, impurity = max, “TWO-POINT” CONTROL) Nu=1: One constraint active Nu=2: No constraints active very unlikely unless there are no purity specifications (e. g. byproducts or recycle) 38

Remaining unconstrained variables: What should we control? (primary controlled variables y 1=c) • Intuition: “Dominant variables” (Shinnar) • Systematic: Minimize cost J(u 0, d*) w. r. t. DOFs u 0. 1. Control active constraints (constant setpoint is optimal) 2. Remaining unconstrained DOFs: Control “self-optimizing” variables c for which constant setpoints cs = copt(d*) give small (economic) loss Loss = J - Jopt(d) when disturbances d ≠ d* occur 39 c = ? (economics) y 2 = ? (stabilization)

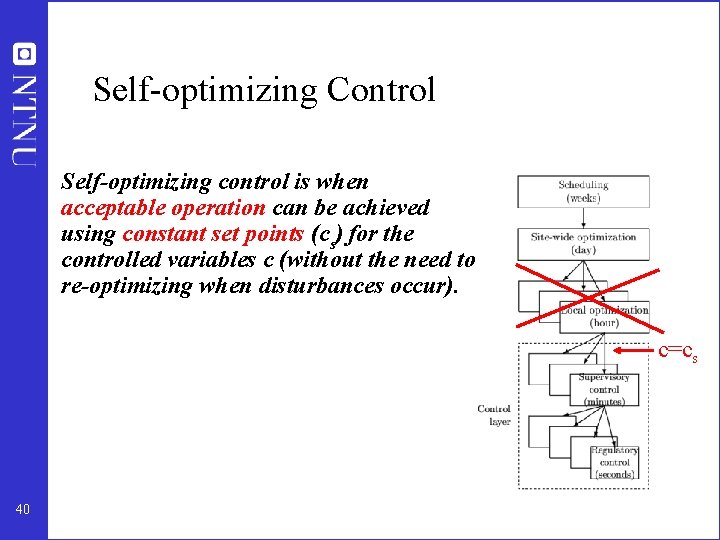
Self-optimizing Control Self-optimizing control is when acceptable operation can be achieved using constant set points (cs) for the controlled variables c (without the need to re-optimizing when disturbances occur). c=cs 40

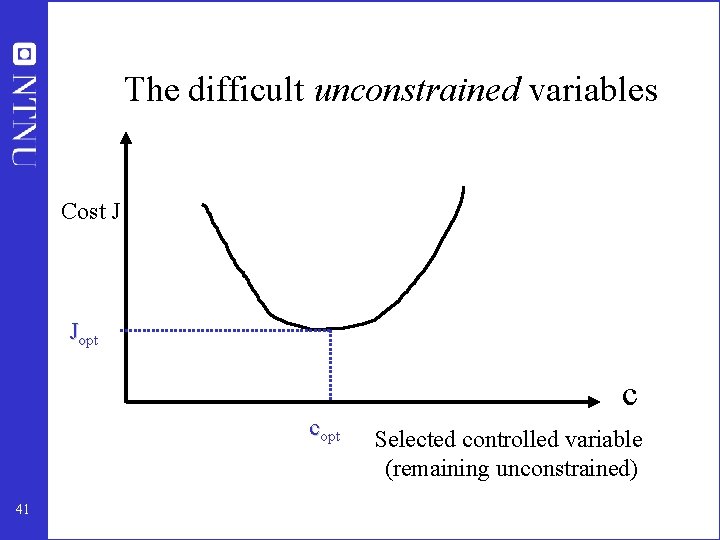
The difficult unconstrained variables Cost J Jopt c copt 41 Selected controlled variable (remaining unconstrained)

Implementation of unconstrained variables is not trivial: How do we deal with uncertainty? • 1. Disturbances d (copt(d) changes) • 2. Implementation error n (actual c ≠ copt) cs = copt(d*) – nominal optimization n c = cs + n d Cost J Jopt(d) 42

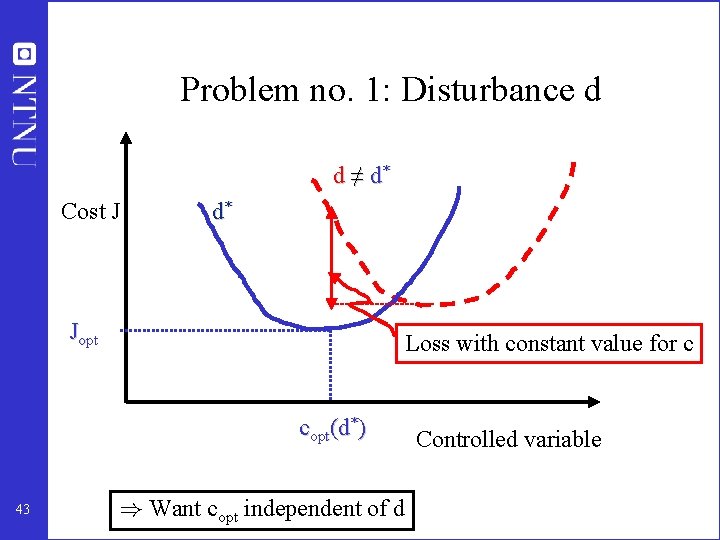
Problem no. 1: Disturbance d d ≠ d* Cost J d* Jopt Loss with constant value for c copt(d*) 43 ) Want copt independent of d Controlled variable

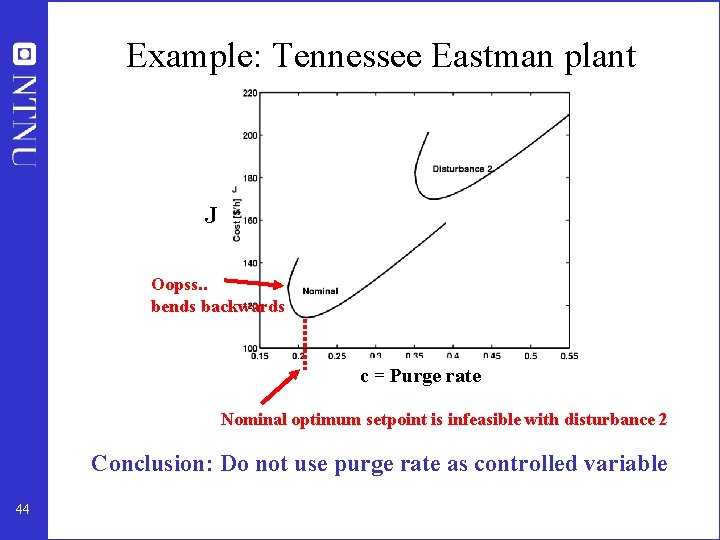
Example: Tennessee Eastman plant J Oopss. . bends backwards c = Purge rate Nominal optimum setpoint is infeasible with disturbance 2 Conclusion: Do not use purge rate as controlled variable 44

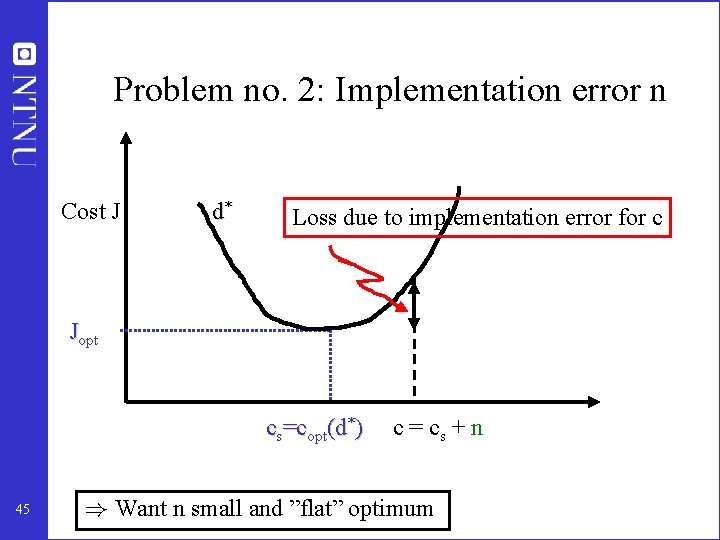
Problem no. 2: Implementation error n Cost J d* Loss due to implementation error for c Jopt cs=copt(d*) 45 c = cs + n ) Want n small and ”flat” optimum

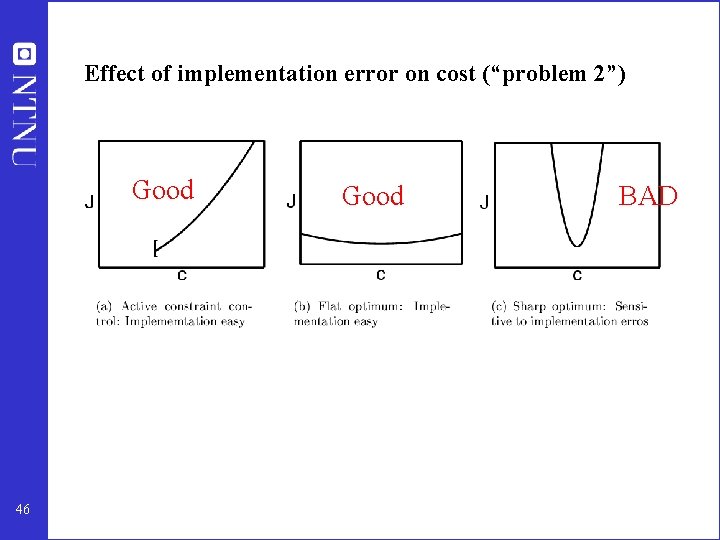
Effect of implementation error on cost (“problem 2”) Good 46 Good BAD

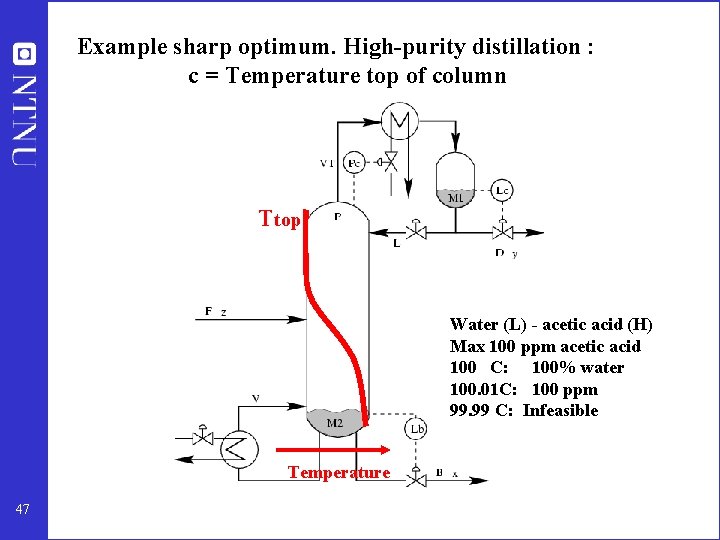
Example sharp optimum. High-purity distillation : c = Temperature top of column Ttop Water (L) - acetic acid (H) Max 100 ppm acetic acid 100 C: 100% water 100. 01 C: 100 ppm 99. 99 C: Infeasible Temperature 47

Summary unconstrained variables: Which variable c to control? • Self-optimizing control: Constant setpoints cs give ”near-optimal operation” (= acceptable loss L for expected disturbances d and implementation errors n) 48 Acceptable loss ) self-optimizing control

Examples self-optimizing control • • Marathon runner Central bank Cake baking Business systems (KPIs) Investment portifolio Biology Chemical process plants: Optimal blending of gasoline Define optimal operation (J) and look for ”magic” variable (c) which when kept constant gives acceptable loss (selfoptimizing control) 49

Self-optimizing Control – Marathon • Optimal operation of Marathon runner, J=T – Any self-optimizing variable c (to control at constant setpoint)? 50

Self-optimizing Control – Marathon • Optimal operation of Marathon runner, J=T – Any self-optimizing variable c (to control at constant setpoint)? • • 51 c 1 = distance to leader of race c 2 = speed c 3 = heart rate c 4 = level of lactate in muscles

Self-optimizing Control – Marathon • Optimal operation of Marathon runner, J=T – Any self-optimizing variable c (to control at constant setpoint)? • • 52 c 1 = distance to leader of race (Problem: Feasibility for d) c 2 = speed (Problem: Feasibility for d) c 3 = heart rate (Problem: Impl. Error n) c 4 = level of lactate in muscles (Problem: Impl. error n)

Self-optimizing Control – Sprinter • Optimal operation of Sprinter (100 m), J=T – Active constraint control: • Maximum speed (”no thinking required”) 53

Further examples • • • Central bank. J = welfare. u = interest rate. c=inflation rate (2. 5%) Cake baking. J = nice taste, u = heat input. c = Temperature (200 C) Business, J = profit. c = ”Key performance indicator (KPI), e. g. – Response time to order – Energy consumption pr. kg or unit – Number of employees – Research spending Optimal values obtained by ”benchmarking” • • Investment (portofolio management). J = profit. c = Fraction of investment in shares (50%) Biological systems: – ”Self-optimizing” controlled variables c have been found by natural selection – Need to do ”reverse engineering” : • • 54 Find the controlled variables used in nature From this possibly identify what overall objective J the biological system has been attempting to optimize

Mathematical: Local analysis cost J uopt 55 u

Unconstrained degrees of freedom: Looking for “magic” variables to keep at constant setpoints. What properties do they have? Skogestad and Postlethwaite (1996): • c-copt should be small: The optimal value of c should be insensitive to disturbances • c should be easy to measure and control accurately • G-1 should be small, i. e (G) should be large: The value of c should be sensitive to changes in the steadystate degrees of freedom (Equivalently, J as a function of c should be flat) 56 • For cases with more than one unconstrained degrees of freedom, the selected controlled variables should be independent. • Summarized by maximum gain (min. singular value) rule Avoid problem 1 (d) Avoid problem 2 (n)

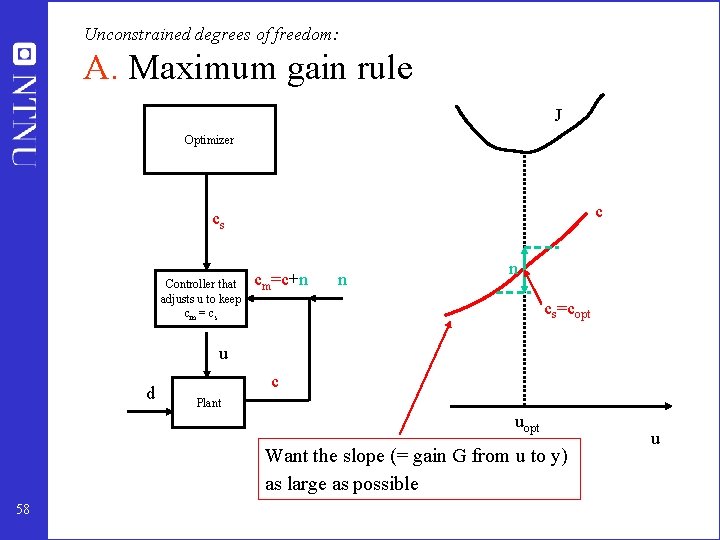
Unconstrained degrees of freedom: Looking for “magic” variables to keep at constant setpoints. How can we find them systematically? A. Maximum gain (minimum singular value) rule: B. “Brute force”: Consider available measurements y, and evaluate loss when they are kept constant: C. More general: Find optimal linear combination (matrix H): 57

Unconstrained degrees of freedom: A. Maximum gain rule J Optimizer c cs Controller that adjusts u to keep cm = cs cm=c+n n n cs=copt u d c Plant uopt Want the slope (= gain G from u to y) as large as possible 58 u

Unconstrained degrees of freedom: A. Maximum gain (minimum singular value) rule “Maximum gain rule” (Skogestad and Postlethwaite, 1996): Look for variables c that maximize the minimum singular value (G) of the appropriately scaled steady-state gain matrix G from u to c • u: unconstrained degrees of freedom • Loss • Scaling is important: – Scale c such that their expected variation is similar (divide by “span”= optimal variation + noise) – Scale inputs u such that they have similar effect on cost J (Juu unitary) • • 59 (G) is called the Morari Resiliency index (MRI) by Luyben Detailed proof: I. J. Halvorsen, S. Skogestad, J. C. Morud and V. Alstad, ``Optimal selection of controlled variables'', Ind. Eng. Chem. Res. , 42 (14), 3273 -3284 (2003).

Maximum gain rule in words Select controlled variables c for which their controllable range is large compared to their sum of optimal variation and control error controllable range = range c may reach by varying the inputs (=gain) optimal variation: due to disturbance span control error = implementation error n 60

What should we control? Rule: Maximize the scaled gain • Scalar case. Minimum singular value = gain |G| • Maximize scaled gain: |Gs| = |G| / span – |G|: gain from independent variable (u) to candidate controlled variable (c) – span (of c) = optimal variation in c + control error for c 61

Generally (more than unconstrained variable): Scaling for “maximum gain ( ) rule” • “Control active constraints” and look at the remaining unconstrained problem • Candidate outputs: Divide by span = optimal range + implementation error • Candidate inputs: – A unit deviation in each input should have the same effect on the cost function (i. e. Juu should be constant times identity) – Alternatively (often simpler), consider (Juu 1/2 G) 62

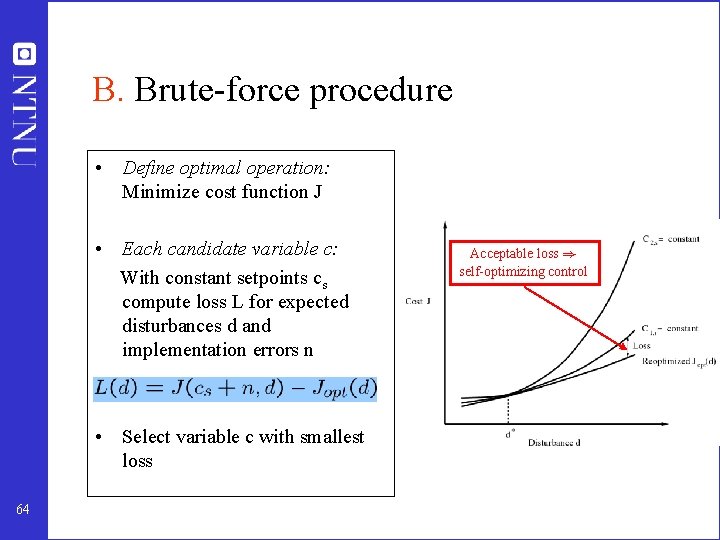
B. “Brute-force” procedure for selecting (primary) controlled variables (Skogestad, 2000) • • Step 1 Determine DOFs for optimization Step 2 Definition of optimal operation J (cost and constraints) Step 3 Identification of important disturbances Step 4 Optimization (nominally and with disturbances) Step 5 Identification of candidate controlled variables (use active constraint control) Step 6 Evaluation of loss with constant setpoints for alternative controlled variables Step 7 Evaluation and selection (including controllability analysis) Case studies: Tenneessee-Eastman, Propane-propylene splitter, recycle process, heat-integrated distillation 63

B. Brute-force procedure • Define optimal operation: Minimize cost function J • Each candidate variable c: With constant setpoints cs compute loss L for expected disturbances d and implementation errors n • Select variable c with smallest loss 64 Acceptable loss ) self-optimizing control

Unconstrained degrees of freedom: C. Optimal measurement combination (Alstad, 2002) Basis: Want optimal value of c independent of disturbances ) – copt = 0 ¢ d • Find optimal solution as a function of d: uopt(d), yopt(d) • Linearize this relationship: yopt = F d • F – sensitivity matrix • Want: • To achieve this for all values of d: • Always possible if • Optimal when we disregard implementation error (n) 65

Alstad-method continued • To handle implementation error: Use “sensitive” measurements, with information about all independent variables (u and d) 66

Toy Example 67

Toy Example 68

Toy Example 69

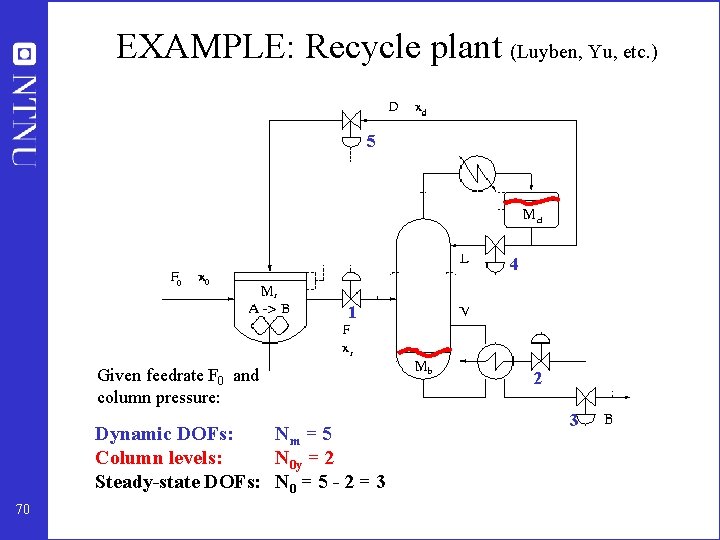
EXAMPLE: Recycle plant (Luyben, Yu, etc. ) 5 4 1 Given feedrate F 0 and column pressure: Dynamic DOFs: Nm = 5 Column levels: N 0 y = 2 Steady-state DOFs: N 0 = 5 - 2 = 3 70 2 3

Recycle plant: Optimal operation m. T 1 remaining unconstrained degree of freedom 71

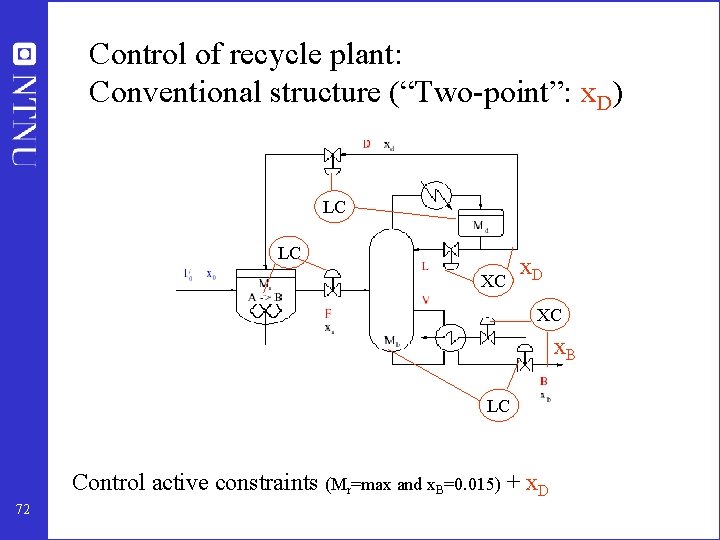
Control of recycle plant: Conventional structure (“Two-point”: x. D) LC LC XC x. D XC x. B LC Control active constraints (Mr=max and x. B=0. 015) + x. D 72

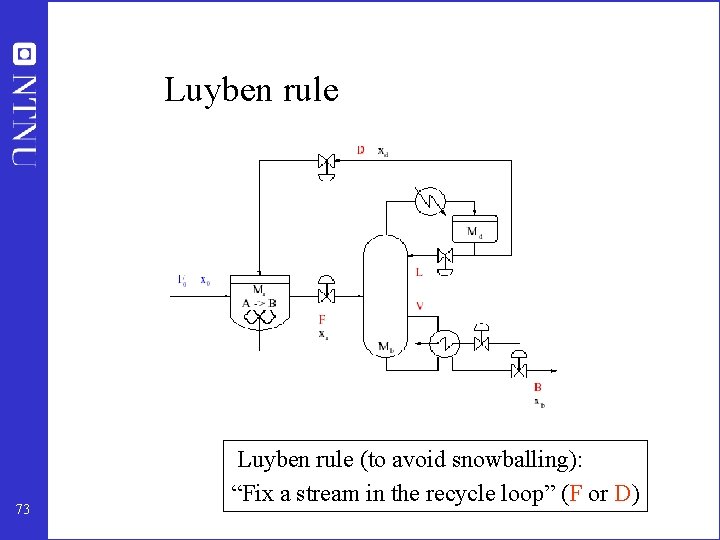
Luyben rule 73 Luyben rule (to avoid snowballing): “Fix a stream in the recycle loop” (F or D)

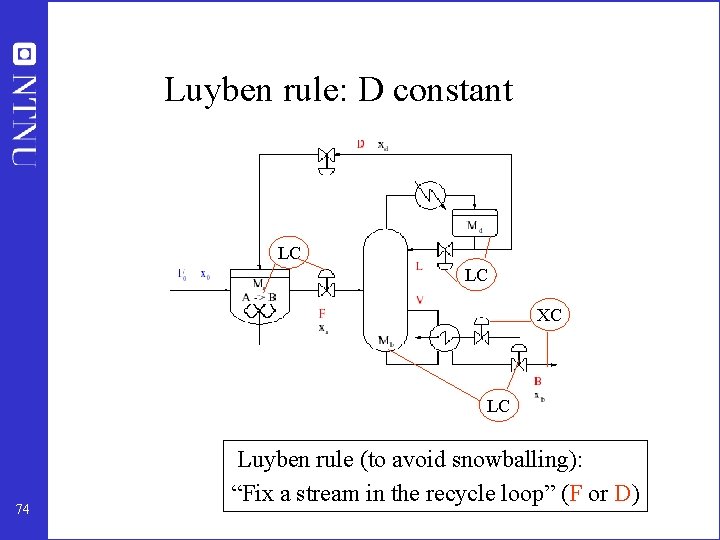
Luyben rule: D constant LC LC XC LC 74 Luyben rule (to avoid snowballing): “Fix a stream in the recycle loop” (F or D)

A. Maximum gain rule: Steady-state gain Conventional: Looks good Luyben rule: Not promising economically 75

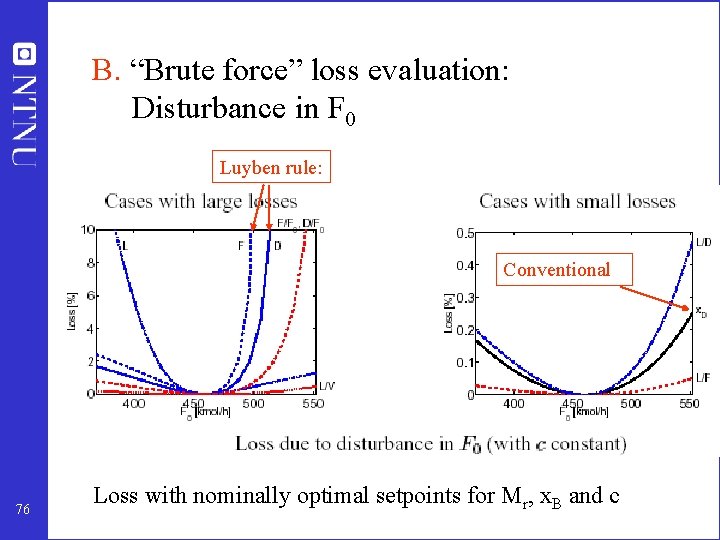
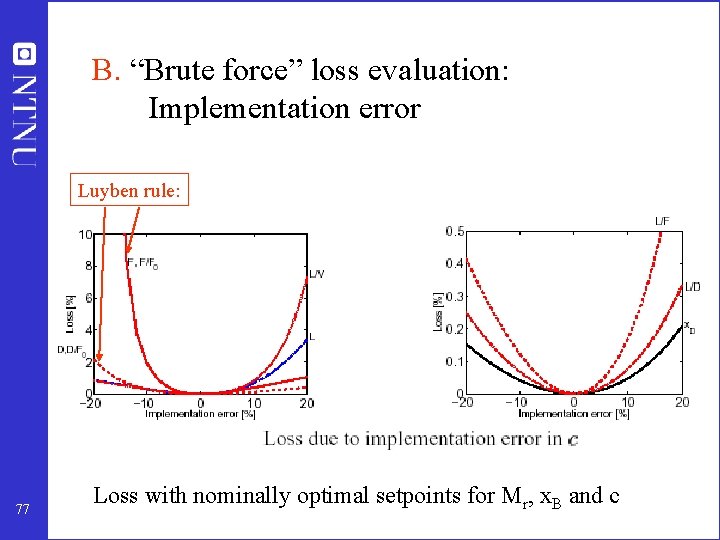
B. “Brute force” loss evaluation: Disturbance in F 0 Luyben rule: Conventional 76 Loss with nominally optimal setpoints for Mr, x. B and c

B. “Brute force” loss evaluation: Implementation error Luyben rule: 77 Loss with nominally optimal setpoints for Mr, x. B and c

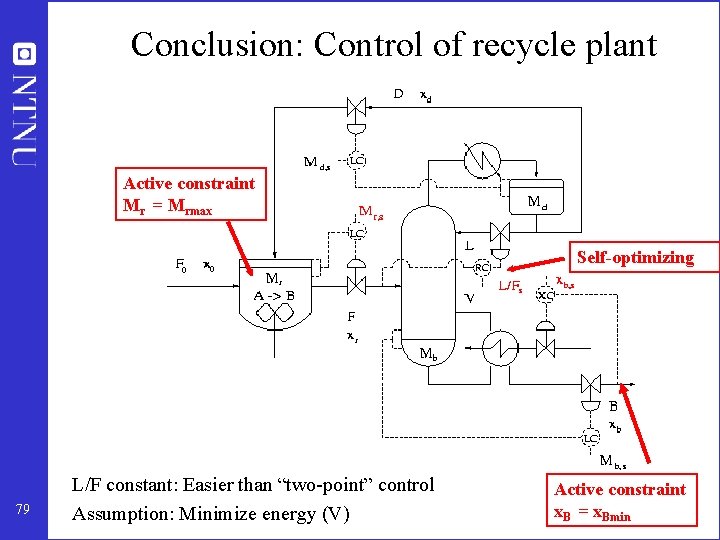
C. Optimal measurement combination • 1 unconstrained variable (#c = 1) • 1 (important) disturbance: F 0 (#d = 1) • “Optimal” combination requires 2 “measurements” (#y = #u + #d = 2) – For example, c = h 1 L + h 2 F • BUT: Not much to be gained compared to control of single variable (e. g. L/F or x. D) 78

Conclusion: Control of recycle plant Active constraint Mr = Mrmax Self-optimizing 79 L/F constant: Easier than “two-point” control Assumption: Minimize energy (V) Active constraint x. B = x. Bmin

Recycle systems: Do not recommend Luyben’s rule of fixing a flow in each recycle loop (even to avoid “snowballing”) 80

Summary: Procedure selection controlled variables 1. 2. 3. 4. Define economics and operational constraints Identify degrees of freedom and important disturbances Optimize for various disturbances Identify (and control) active constraints (off-line calculations) • May vary depending on operating region. For each operating region do step 5: 5. Identify “self-optimizing” controlled variables for remaining degrees of freedom 1. (A) Identify promising (single) measurements from “maximize gain rule” (gain = minimum singular value) • (C) Possibly consider measurement combinations if no promising 2. (B) “Brute force” evaluation of loss for promising alternatives • • Necessary because “maximum gain rule” is local. In particular: Look out for feasibility problems. 3. Controllability evaluation for promising alternatives 81

Selection of controlled variables More examples and exercises • • 82 HDA process Cooling cycle Distillation (C 3 -splitter) Blending

Summary ”self-optimizing” control • Operation of most real system: Constant setpoint policy (c = cs) – – • Central bank Business systems: KPI’s Biological systems Chemical processes Goal: Find controlled variables c such that constant setpoint policy gives acceptable operation in spite of uncertainty ) Self-optimizing control • • • Method A: Maximize (G) Method B: Evaluate loss L = J - Jopt Method C: Optimal linear measurement combination: c = H y where HF=0 83

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimzing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 84

Step 4. Where set production rate? • • 85 Very important! Determines structure of remaining inventory (level) control system Set production rate at (dynamic) bottleneck Link between Top-down and Bottom-up parts

Production rate set at inlet : Inventory control in direction of flow 86

Production rate set at outlet: Inventory control opposite flow 87

Production rate set inside process 88

Where set the production rate? • Very important decision that determines the structure of the rest of the control system! • May also have important economic implications 89

Often optimal: Set production rate at bottleneck! • "A bottleneck is an extensive variable that prevents an increase in the overall feed rate to the plant" • If feed is cheap and available: Optimal to set production rate at bottleneck • If the flow for some time is not at its maximum through the bottleneck, then this loss can never be recovered. 90

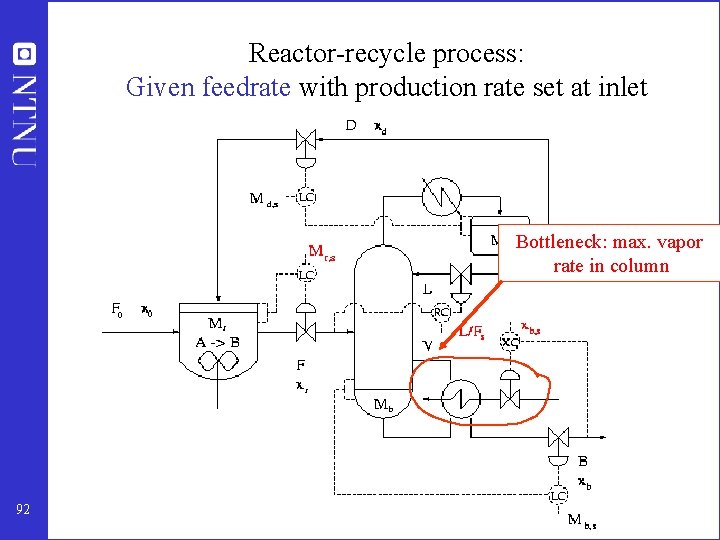
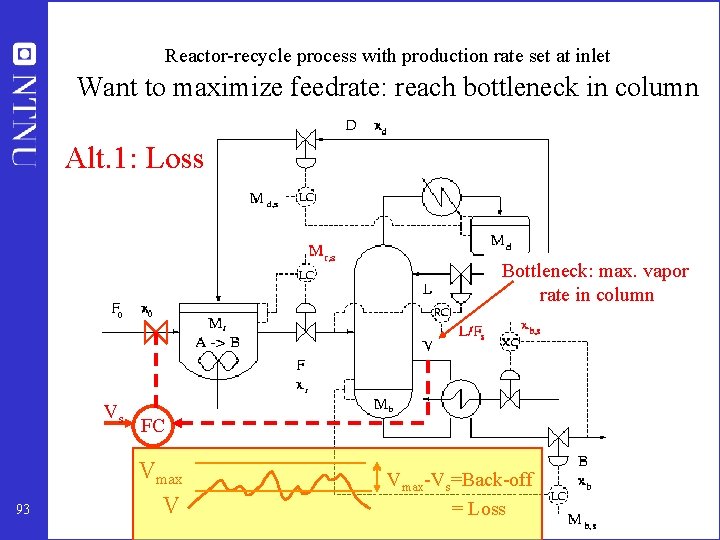
Reactor-recycle process: Given feedrate with production rate set at inlet 91

Reactor-recycle process: Given feedrate with production rate set at inlet Bottleneck: max. vapor rate in column 92

Reactor-recycle process with production rate set at inlet Want to maximize feedrate: reach bottleneck in column Alt. 1: Loss Bottleneck: max. vapor rate in column Vs 93 FC Vmax V Vmax-Vs=Back-off = Loss

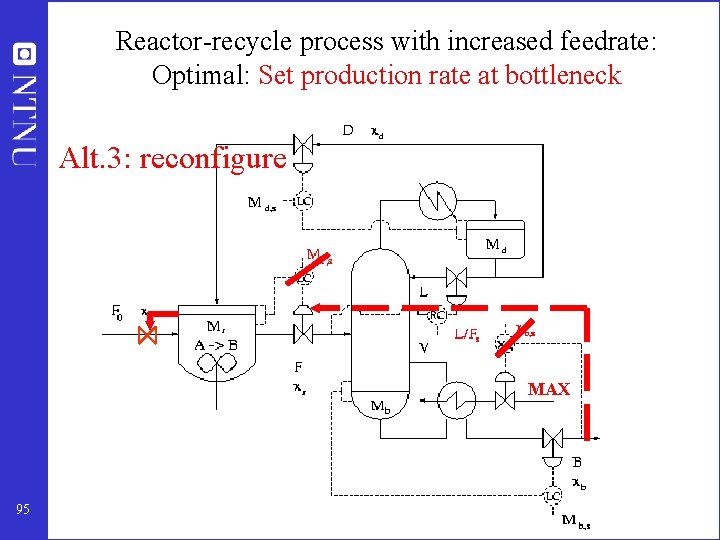
Reactor-recycle process with increased feedrate: Optimal: Set production rate at bottleneck Alt. 2 “long loop” MAX 94

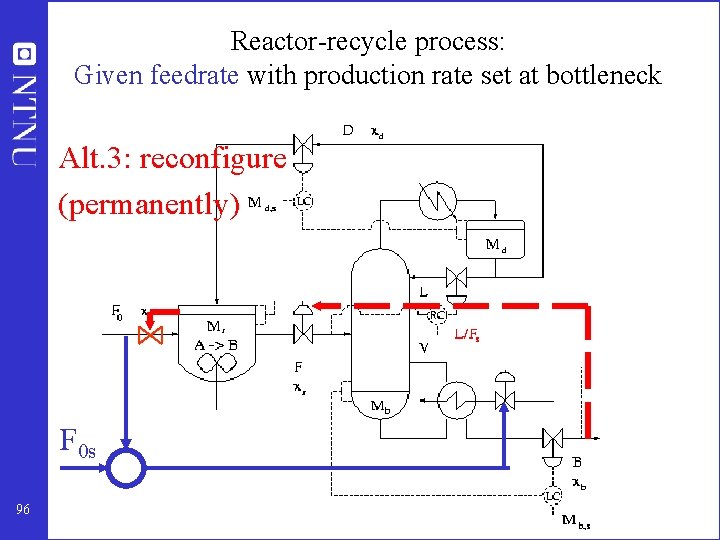
Reactor-recycle process with increased feedrate: Optimal: Set production rate at bottleneck Alt. 3: reconfigure MAX 95

Reactor-recycle process: Given feedrate with production rate set at bottleneck Alt. 3: reconfigure (permanently) F 0 s 96

Alt. 4: Multivariable control (MPC) • Can reduce loss • BUT: Is generally placed on top of the regulatory control system (including level loops), so it still important where the production rate is set! 97

Conclusion production rate manipulator • Think carefully about where to place it! • Difficult to undo later 98

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 99

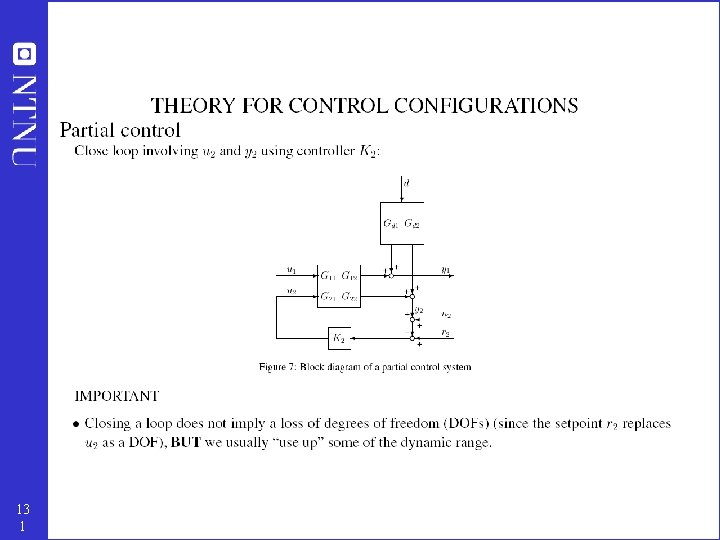
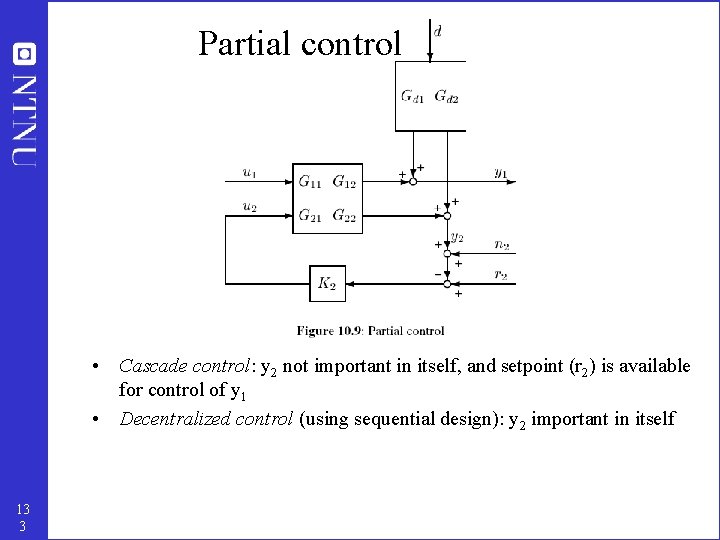
II. Bottom-up • Determine secondary controlled variables and structure (configuration) of control system (pairing) • A good control configuration is insensitive to parameter changes Step 5. REGULATORY CONTROL LAYER 5. 1 Stabilization (including level control) 5. 2 Local disturbance rejection (inner cascades) What more to control? (secondary variables) Step 6. SUPERVISORY CONTROL LAYER Decentralized or multivariable control (MPC)? Pairing? Step 7. OPTIMIZATION LAYER (RTO) 10 0

Example: Distillation • Primary controlled variable: y 1 = c = x. D, x. B (compositions top, bottom) • BUT: Delay in measurement of x + unreliable • Regulatory control: For “stabilization” need control of: – – 10 1 Liquid level condenser (MD) Unstable (Integrating) + No steady-state effect Liquid level reboiler (MB) Disturbs (“destabilizes”) other loops Pressure (p) Holdup of light component in column (temperature profile) Almost unstable (integrating)

Step 5. Regulatory control layer • Purpose: “Stabilize” the plant using local SISO PID controllers • Enable manual operation (by operators) • Main structural issues: • What more should we control? (secondary cv’s, y 2) • Pairing with manipulated variables (mv’s u 2) y 1 = c y 2 = ? 10 2

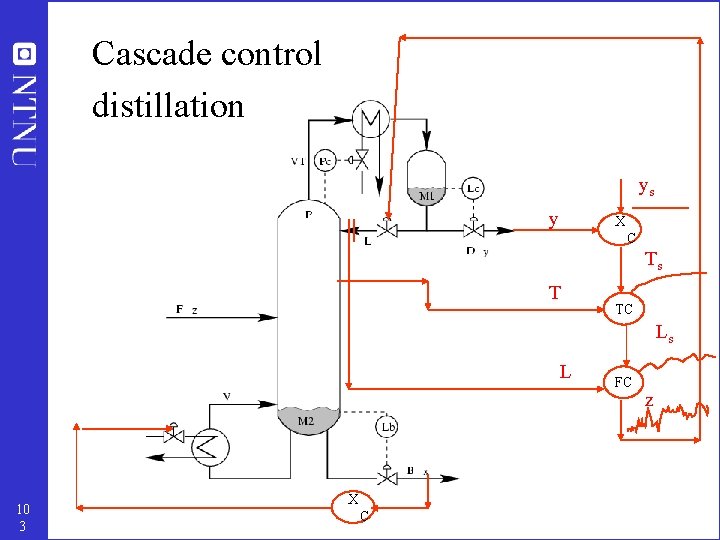
Cascade control distillation ys y X C Ts T TC Ls L 10 3 X C FC z

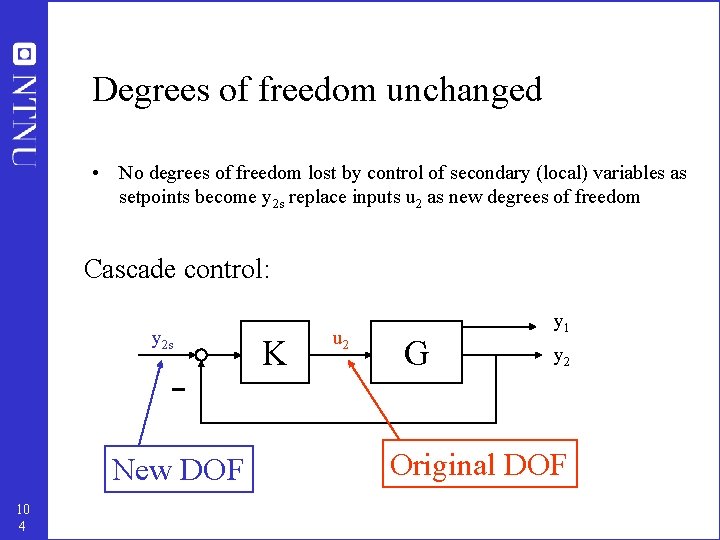
Degrees of freedom unchanged • No degrees of freedom lost by control of secondary (local) variables as setpoints become y 2 s replace inputs u 2 as new degrees of freedom Cascade control: y 2 s New DOF 10 4 K u 2 G y 1 y 2 Original DOF

Hierarchical control: Time scale separation • With a “reasonable” time scale separation between the layers (typically by a factor 5 or more in terms of closed-loop response time) we have the following advantages: 1. The stability and performance of the lower (faster) layer (involving y 2) is not much influenced by the presence of the upper (slow) layers (involving y 1) Reason: The frequency of the “disturbance” from the upper layer is well inside the bandwidth of the lower layers 2. With the lower (faster) layer in place, the stability and performance of the upper (slower) layers do not depend much on the specific controller settings used in the lower layers Reason: The lower layers only effect frequencies outside the bandwidth of the upper layers 10 5

Objectives regulatory control layer 1. 2. 3. 4. 5. 6. 7. Allow for manual operation Simple decentralized (local) PID controllers that can be tuned on-line Take care of “fast” control Track setpoint changes from the layer above Local disturbance rejection Stabilization (mathematical sense) Avoid “drift” (due to disturbances) so system stays in “linear region” – “stabilization” (practical sense) 8. Allow for “slow” control in layer above (supervisory control) 9. Make control problem easy as seen from layer above 10 6 Implications for selection of y 2: 1. Control of y 2 “stabilizes the plant” 2. y 2 is easy to control (favorable dynamics)

1. “Control of y 2 stabilizes the plant” A. “Mathematical stabilization” (e. g. reactor): • Unstable mode is “quickly” detected (state observability) in the measurement (y 2) and is easily affected (state controllability) by the input (u 2). • Tool for selecting input/output: Pole vectors – y 2: Want large element in output pole vector: Instability easily detected relative to noise – u 2: Want large element in input pole vector: Small input usage required for stabilization 10 7 B. “Practical extended stabilization” (avoid “drift” due to disturbance sensitivity): • Intuitive: y 2 located close to important disturbance • Or rather: Controllable range for y 2 is large compared to sum of optimal variation and control error • More exact tool: Partial control analysis

Recall rule for selecting primary controlled variables c: Controlled variables c for which their controllable range is large compared to their sum of optimal variation and control error Restated for secondary controlled variables y 2: Control variables y 2 for which their controllable range is large compared to their sum of optimal variation and control error controllable range = range y 2 may reach by varying the inputs optimal variation: due to disturbances Want small control error = implementation error n 10 8 Want large

What should we control (y 2)? Rule: Maximize the scaled gain • • Scalar case. Minimum singular value = gain |G| Maximize scaled gain: |Gs| = |G| / span – |G|: gain from independent variable (u) to candidate controlled variable (y) – span (of y) = optimal variation in c + control error for y • Note optimal variation: This is generally NOT the same as the optimal variation used for selecting primary controlled variables (c) because we at the “fast” regulatory time scale have that the “slower” (unused) inputs (u 1) are constant. – 10 9 For each disturbance find optimal input change (u 2) that keeps primary variables c=y 1 closest to setpoint (with u 1 constant), and from this obtain optimal variation (copt)

2. “y 2 is easy to control” • Main rule: y 2 is easy to measure and located close to manipulated variable u 2 • Statics: Want large gain (from u 2 to y 2) • Dynamics: Want small effective delay (from u 2 to y 2) 11 0

Aside: Effective delay and tunings • PI-tunings from “SIMC rule” • Use half rule to obtain first-order model – Effective delay θ = “True” delay + inverse response time constant + half of second time constant + all smaller time constants – Time constant τ1 = original time constant + half of second time constant – NOTE: The first (largest) time constant is NOT important for controllability! 11 1

Summary: Rules for selecting y 2 1. y 2 should be easy to measure 2. Control of y 2 stabilizes the plant 3. y 2 should have good controllability, that is, favorable dynamics for control 4. y 2 should be located “close” to a manipulated input (u 2) (follows from rule 3) 5. The (scaled) gain from u 2 to y 2 should be large • 11 2 Additional rule for selecting u 2: Avoid using inputs u 2 that may saturate (should generally avoid saturation in lower layers)

Exercise level control (10. 1 in Seborg) • Consider control of liquid condenser level (M 1) in a distillation column. – Should we use L or D to control M 1? – What is your answer if L/D=5? – What is your answer if it is important to avoid disturbing downstream process? 11 3

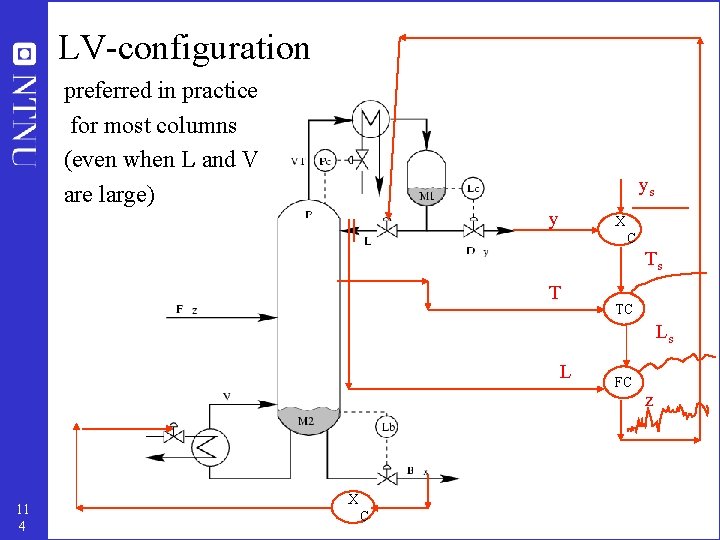
LV-configuration preferred in practice for most columns (even when L and V are large) ys y X C Ts T TC Ls L 11 4 X C FC z

Exercise distillation (10. 3 in Seborg) • Consider a column design to separate methanol and water. The desired distillate composition (x. D) is methanol with only 5 ppm of water. Because a composition analyzer is not available, it is proposed to control XD indirectly by measuring and controlling a temperature at one of the following locations (a) the reflux stream (b) the top tray (stage) of the column (c) an intermediate tray in the top section (where? ) Discuss the relative advantages and disadvantages of each choice based on both steady-state and dynamic considerations 11 5

More exact: Selecting stage for temperature control (y 2) in distillation • • • Consider controlling temperature (y=T) with reflux (u=L) – Avoid V because it may saturate (i. e. reach maximum) – This is generally NOT the same as the optimal variation used for selecting primary controlled variables (c) because we have to assume that the “slower” variables (e. g. u 1=V) are constant. Here: We want to control product compositions. The optimal variation in T will be small towards the end of the column and largest toward the feed stage G= “Controllable range”: Given by gain T/ L (“sensitivity”). This will be largest where temperature changes are the largest, that is, toward the feed stage for a binary separation Topt = “Optimal variation” for disturbances (in F, z. F, etc. ): – • • Terr = “Control error” (=implementation error = static measurement error) – This will typically be 0. 5 C and the same on stages Rule: Select location corresponding to max. value of – • • 11 6 G / (Topt + Terr) Binary separation: This will have a max. in the middle of the top section and middle of bottom section Multicomponent separation: Will have a max. towards column ends

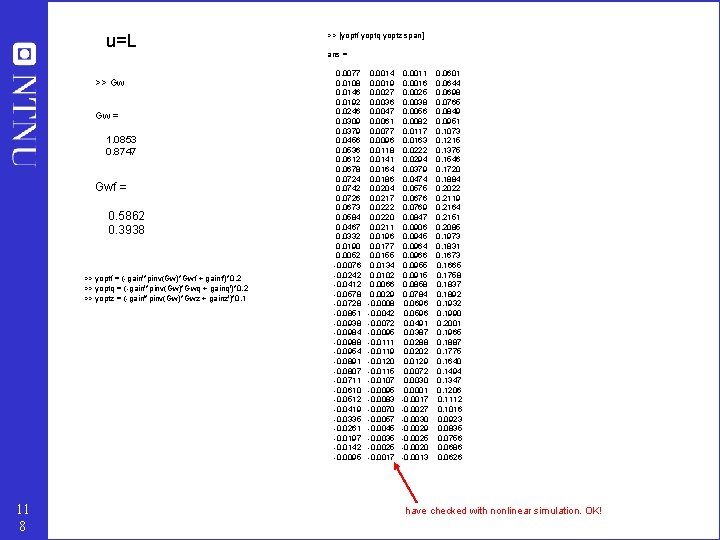
Distillation example columnn A. u=L. Which temperature (c) to control? 1. Nominal simulation (gives x 0) 2. One simulation: Gain with constant inputs (u) – Make small change in input (L) with the other inputs (V) constant Find gain = xi/ L 3. From process gains: Obtain “optimal” change for candidate measurements to disturbances, (with input L adjusted to keep both x. D and x. B close to setpoint, i. e. min ||x. D-0. 99; xb-0. 01|| , with V=constant). w=[x. B, x. D]. Then (- Gy pinv(Gw) Gwd + Gyd) d (Note: Gy=gain, d=F: Gyd=gainf etc. ) Find xi, opt (yopt) for the following disturbances 1. 2. 3. 4. 4. 5. 11 7 F (from 1 to 1. 2; has effect!) z. F from 0. 5 to 0. 6 q. F from 1 to 1. 2 x. B from 0. 01 to 0. 02 yoptf yoptz yoptq yoptxb=0 (no effect) Control (implementation) error. Assume=0. 05 on all stages Find scaled-gain = gain/span where span = abs(yoptf)+abs(yoptz)+abs(yoptq)+0. 05 “Maximize gain rule”: Prefer stage where scaled-gain is large >> res=[x 0' gainf' gainz' gainq'] res = 0. 0100 1. 0853 0. 5862 1. 1195 1. 0930 0. 0143 1. 5396 0. 8311 1. 5893 1. 5506 0. 0197 2. 1134 1. 1397 2. 1842 2. 1285 0. 0267 2. 8310 1. 5247 2. 9303 2. 8513 0. 0355 3. 7170 1. 9990 3. 8539 3. 7437 0. 0467 4. 7929 2. 5734 4. 9789 4. 8273 0. 0605 6. 0718 3. 2542 6. 3205 6. 1155 0. 0776 7. 5510 4. 0392 7. 8779 7. 6055 0. 0982 9. 2028 4. 9126 9. 6244 9. 2694 0. 1229 10. 9654 5. 8404 11. 4975 11. 0449 0. 1515 12. 7374 6. 7676 13. 3931 12. 8301 0. 1841 14. 3808 7. 6202 15. 1675 14. 4857 0. 2202 15. 7358 8. 3133 16. 6530 15. 8509 0. 2587 16. 6486 8. 7659 17. 6861 16. 7709 0. 2986 17. 0057 8. 9194 18. 1436 17. 1311 0. 3385 16. 7628 8. 7524 17. 9737 16. 8870 0. 3770 15. 9568 8. 2872 17. 2098 16. 0758 0. 4130 14. 6955 7. 5832 15. 9597 14. 8058 0. 4455 13. 1286 6. 7215 14. 3776 13. 2280 0. 4742 11. 4148 5. 7872 12. 6286 11. 5021 0. 4987 9. 6930 4. 8542 10. 8586 9. 7680 0. 5265 11. 0449 5. 4538 12. 1996 11. 1051 0. 5578 12. 2975 6. 0007 13. 4225 12. 3410 0. 5922 13. 3469 6. 4473 14. 4211 13. 3727 0. 6290 14. 0910 6. 7478 15. 0929 14. 0989 0. 6675 14. 4487 6. 8669 15. 3588 14. 4397 0. 7065 14. 3766 6. 7871 15. 1800 14. 3528 0. 7449 13. 8797 6. 5135 14. 5676 13. 8438 0. 7816 13. 0098 6. 0724 13. 5807 12. 9654 0. 8158 11. 8545 5. 5060 12. 3136 11. 8051 0. 8469 10. 5187 4. 8635 10. 8764 10. 4677 0. 8744 9. 1066 4. 1929 9. 3765 9. 0566 0. 8983 7. 7071 3. 5346 7. 9044 7. 6602 0. 9187 6. 3866 2. 9184 6. 5261 6. 3443 0. 9358 5. 1876 2. 3624 5. 2829 5. 1505 0. 9501 4. 1314 1. 8756 4. 1942 4. 1000 0. 9617 3. 2233 1. 4592 3. 2631 3. 1975 0. 9712 2. 4574 1. 1098 2. 4816 2. 4368 0. 9789 1. 8211 0. 8208 1. 8355 1. 8053 0. 9851 1. 2990 0. 5848 1. 3077 1. 2875 0. 9900 0. 8747 0. 3938 0. 8805 0. 8670

u=L >> Gw Gw = 1. 0853 0. 8747 Gwf = 0. 5862 0. 3938 >> yoptf = (-gain'*pinv(Gw)*Gwf + gainf')*0. 2 >> yoptq = (-gain'*pinv(Gw)*Gwq + gainq')*0. 2 >> yoptz = (-gain'*pinv(Gw)*Gwz + gainz')*0. 1 11 8 >> [yoptf yoptq yoptz span] ans = 0. 0077 0. 0014 0. 0011 0. 0601 0. 0108 0. 0019 0. 0016 0. 0644 0. 0146 0. 0027 0. 0025 0. 0698 0. 0192 0. 0036 0. 0038 0. 0765 0. 0246 0. 0047 0. 0056 0. 0849 0. 0309 0. 0061 0. 0082 0. 0951 0. 0379 0. 0077 0. 0117 0. 1073 0. 0456 0. 0096 0. 0163 0. 1215 0. 0536 0. 0118 0. 0222 0. 1375 0. 0612 0. 0141 0. 0294 0. 1546 0. 0678 0. 0164 0. 0379 0. 1720 0. 0724 0. 0186 0. 0474 0. 1884 0. 0742 0. 0204 0. 0575 0. 2022 0. 0726 0. 0217 0. 0676 0. 2119 0. 0673 0. 0222 0. 0769 0. 2164 0. 0584 0. 0220 0. 0847 0. 2151 0. 0467 0. 0211 0. 0906 0. 2085 0. 0332 0. 0196 0. 0945 0. 1973 0. 0190 0. 0177 0. 0964 0. 1831 0. 0052 0. 0155 0. 0966 0. 1673 -0. 0076 0. 0134 0. 0955 0. 1665 -0. 0242 0. 0102 0. 0915 0. 1758 -0. 0412 0. 0066 0. 0858 0. 1837 -0. 0578 0. 0029 0. 0784 0. 1892 -0. 0728 -0. 0008 0. 0696 0. 1932 -0. 0851 -0. 0042 0. 0596 0. 1990 -0. 0938 -0. 0072 0. 0491 0. 2001 -0. 0984 -0. 0095 0. 0387 0. 1965 -0. 0988 -0. 0111 0. 0288 0. 1887 -0. 0954 -0. 0119 0. 0202 0. 1775 -0. 0891 -0. 0120 0. 0129 0. 1640 -0. 0807 -0. 0115 0. 0072 0. 1494 -0. 0711 -0. 0107 0. 0030 0. 1347 -0. 0610 -0. 0095 0. 0001 0. 1206 -0. 0512 -0. 0083 -0. 0017 0. 1112 -0. 0419 -0. 0070 -0. 0027 0. 1016 -0. 0335 -0. 0057 -0. 0030 0. 0923 -0. 0261 -0. 0045 -0. 0029 0. 0835 -0. 0197 -0. 0035 -0. 0025 0. 0756 -0. 0142 -0. 0025 -0. 0020 0. 0686 -0. 0095 -0. 0017 -0. 0013 0. 0626 have checked with nonlinear simulation. OK!

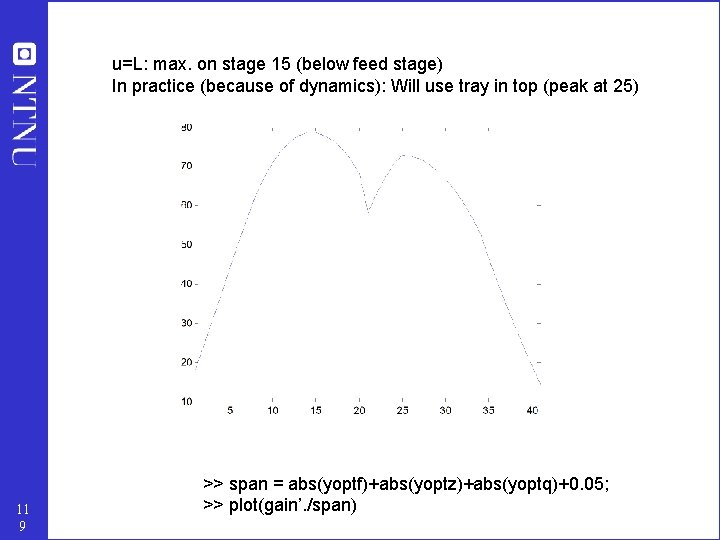
u=L: max. on stage 15 (below feed stage) In practice (because of dynamics): Will use tray in top (peak at 25) 11 9 >> span = abs(yoptf)+abs(yoptz)+abs(yoptq)+0. 05; >> plot(gain’. /span)

NOT QUITE CORRECT: Using scalings from selection of primary variables stage 31 TOP variation=yoptz+yoptq+yoptxb+0. 05 plot(gain. /variation) 12 0

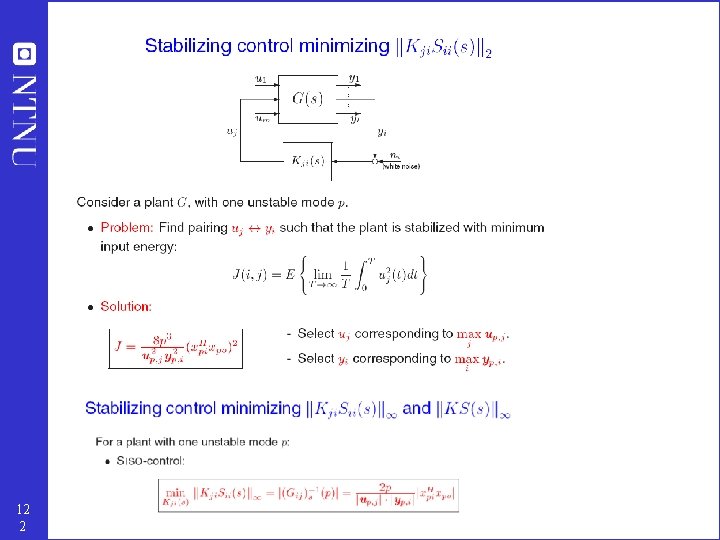
Another tool for stabilization: Pole vectors • Maximum gain rule is good for integrating (drifting) modes • For “fast” unstable modes (e. g. reactor): Pole vectors useful for determining which input (valve) and output (measurement) to use for stabilizing unstable modes • Assumes input usage (avoiding saturation) may be a problem 12 1

12 2

12 3

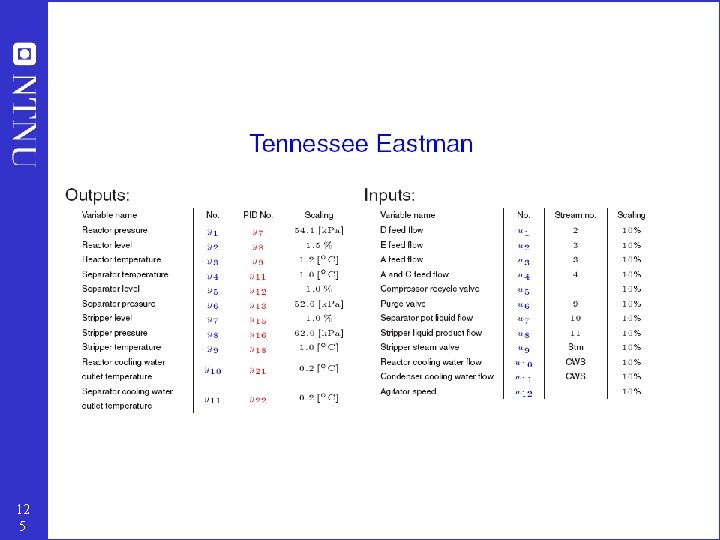
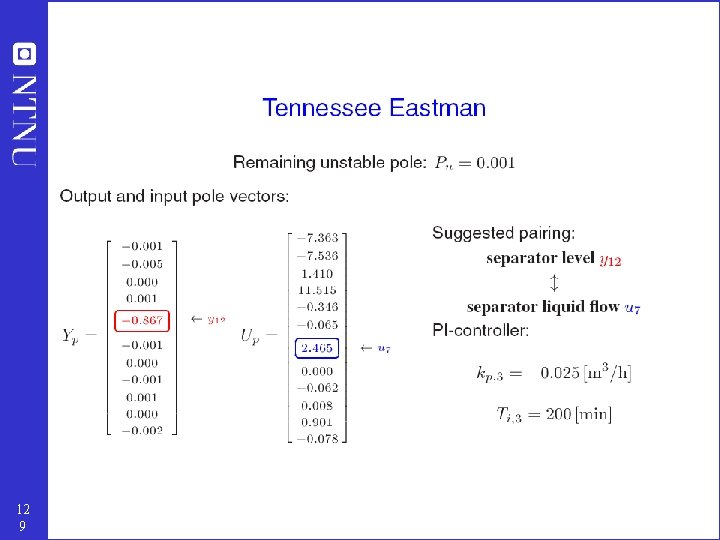
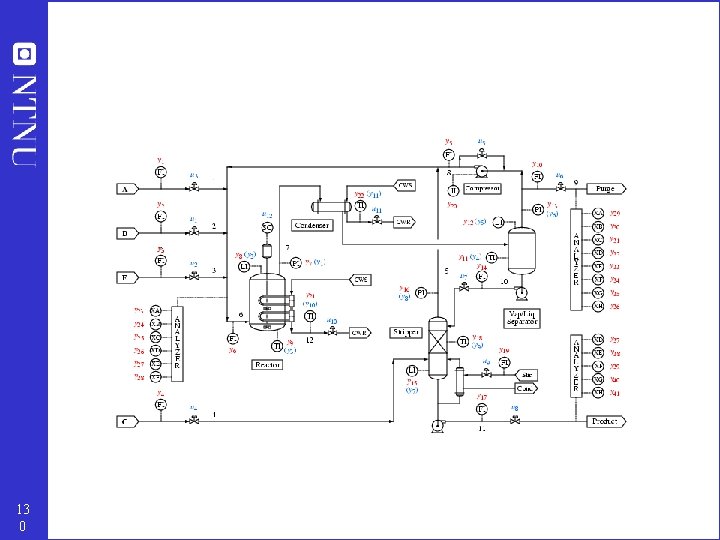
Example: Tennessee Eastman challenge problem 12 4

12 5

12 6

12 7

12 8

12 9

13 0

13 1

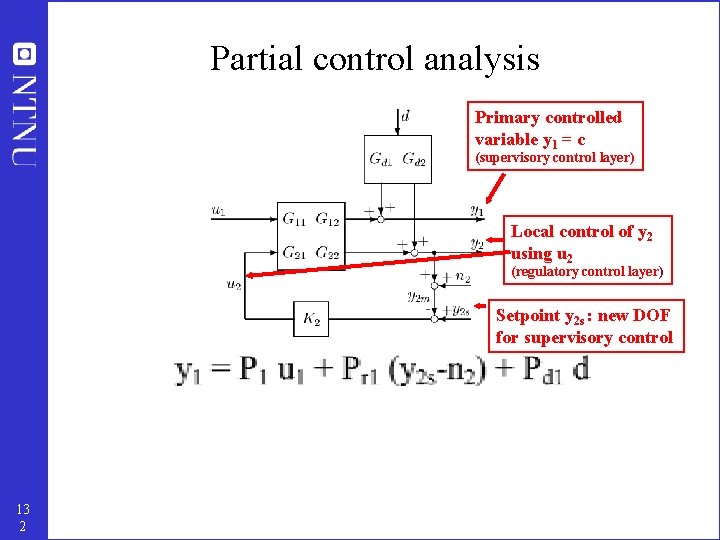
Partial control analysis Primary controlled variable y 1 = c (supervisory control layer) Local control of y 2 using u 2 (regulatory control layer) Setpoint y 2 s : new DOF for supervisory control 13 2

Partial control • Cascade control: y 2 not important in itself, and setpoint (r 2) is available for control of y 1 • Decentralized control (using sequential design): y 2 important in itself 13 3

Limitations of partial control? • Cascade control: Closing of secondary loops does not by itself impose new problems – Theorem 10. 2. The partially controlled system [P 1 Pr 1] from [u 1 r 2] to y 1 has no new RHP-zeros that are not present in the open-loop system [G 11 G 12] from [u 1 u 2] to y 1 provided • r 2 is available for control of y 1 • K 2 has no RHP-zeros • Decentralized control (sequential design): Can introduce limitations. – Avoid pairing on negative RGA for u 2/y 2 – otherwise Pu likely has a RHPzero 13 4

13 5

13 6

13 7

13 8

13 9

14 0

Control configuration elements • Control configuration. The restrictions imposed on the overall controller by decomposing it into a set of local controllers (subcontrollers, units, elements, blocks) with predetermined links and with a possibly predetermined design sequence where subcontrollers are designed locally. Control configuration elements: • Cascade controllers • Decentralized controllers • Feedforward elements • Decoupling elements 14 1

• • • 14 2 Cascade control arises when the output from one controller is the input to another. This is broader than the conventional definition of cascade control which is that the output from one controller is the reference command (setpoint) to another. In addition, in cascade control, it is usually assumed that the inner loop K 2 is much faster than the outer loop K 1. Feedforward elements link measured disturbances to manipulated inputs. Decoupling elements link one set of manipulated inputs (“measurements”) with another set of manipulated inputs. They are used to improve the performance of decentralized control systems, and are often viewed as feedforward elements (although this is not correct when we view the control system as a whole) where the “measured disturbance” is the manipulated input computed by another decentralized controller.

Why simplified configurations? • Fundamental: Save on modelling effort • Other: – – – 14 3 easy to understand easy to tune and retune insensitive to model uncertainty possible to design for failure tolerance fewer links reduced computation load

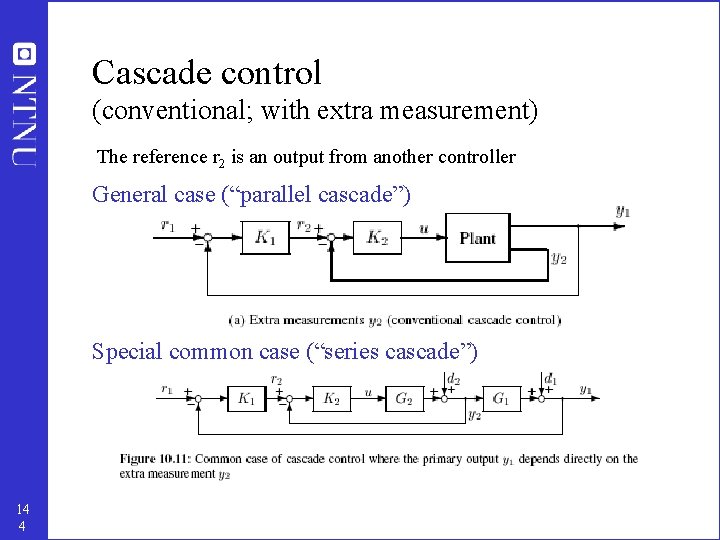
Cascade control (conventional; with extra measurement) The reference r 2 is an output from another controller General case (“parallel cascade”) Special common case (“series cascade”) 14 4

Series cascade 1. 2. 3. Disturbances arising within the secondary loop (before y 2) are corrected by the secondary controller before they can influence the primary variable y 1 Phase lag existing in the secondary part of the process (G 2) is reduced by the secondary loop. This improves the speed of response of the primary loop. Gain variations in G 2 are overcome within its own loop. Thus, use cascade control (with an extra secondary measurement y 2) when: • The disturbance d 2 is significant and G 1 has an effective delay • The plant G 2 is uncertain (varies) or n onlinear 14 5 Design: • First design K 2 (“fast loop”) to deal with d 2 • Then design K 1 to deal with d 1

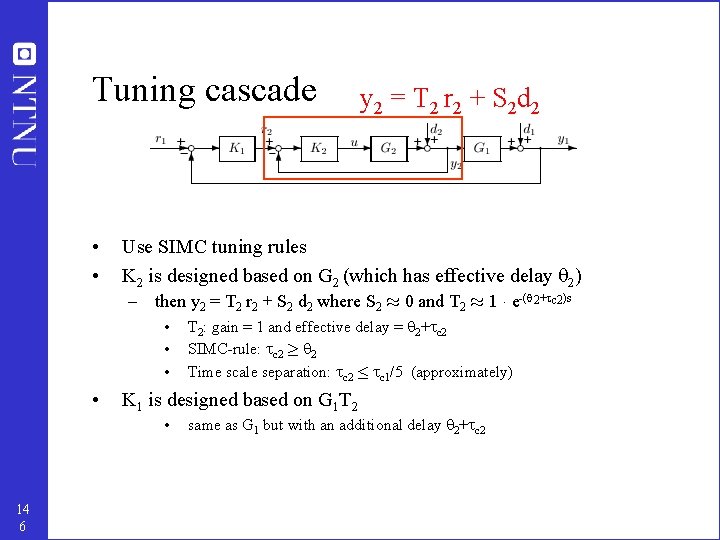
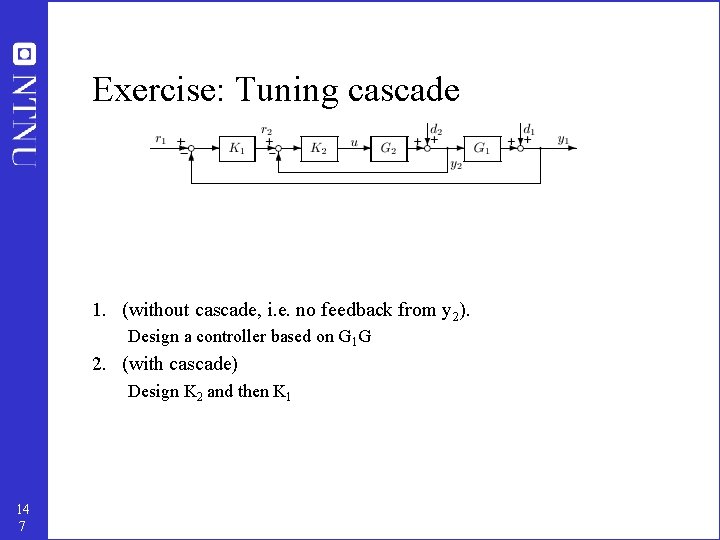
Tuning cascade • • y 2 = T 2 r 2 + S 2 d 2 Use SIMC tuning rules K 2 is designed based on G 2 (which has effective delay 2) – then y 2 = T 2 r 2 + S 2 d 2 where S 2 ¼ 0 and T 2 ¼ 1 ¢ e-( 2+ c 2)s • • K 1 is designed based on G 1 T 2 • 14 6 T 2: gain = 1 and effective delay = 2+ c 2 SIMC-rule: c 2 ¸ 2 Time scale separation: c 2 · c 1/5 (approximately) same as G 1 but with an additional delay 2+ c 2

Exercise: Tuning cascade 1. (without cascade, i. e. no feedback from y 2). Design a controller based on G 1 G 2. (with cascade) Design K 2 and then K 1 14 7

Exercise: Tuning cascade 14 8

Extra inputs • Exercise: Explain how “valve position control” fits into this framework. As en example consider a heat exchanger with bypass 14 9

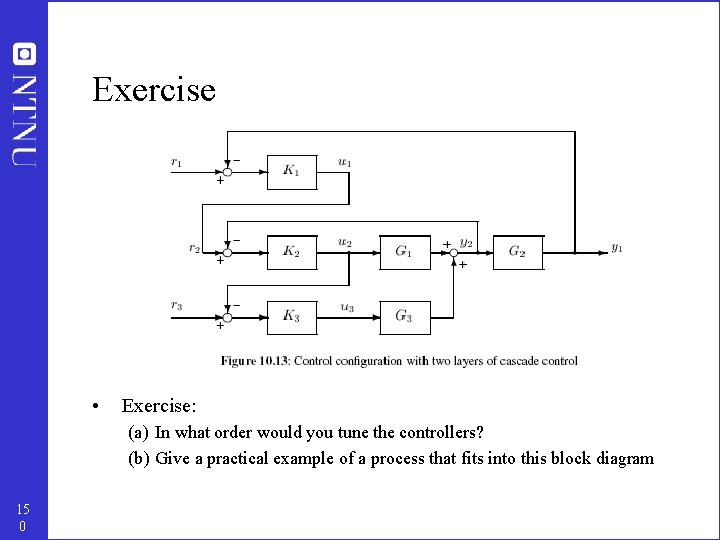
Exercise • Exercise: (a) In what order would you tune the controllers? (b) Give a practical example of a process that fits into this block diagram 15 0

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (primary CV’s) (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control (secondary CV’s) ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 15 1

Step 6. Supervisory control layer • Purpose: Keep primary controlled outputs c=y 1 at optimal setpoints cs • Degrees of freedom: Setpoints y 2 s in reg. control layer • Main structural issue: Decentralized or multivariable? 15 2

Decentralized control (single-loop controllers) Use for: Noninteracting process and no change in active constraints + Tuning may be done on-line + No or minimal model requirements + Easy to fix and change - Need to determine pairing - Performance loss compared to multivariable control - Complicated logic required for reconfiguration when active constraints move 15 3

Multivariable control (with explicit constraint handling = MPC) Use for: Interacting process and changes in active constraints + Easy handling of feedforward control + Easy handling of changing constraints • no need for logic • smooth transition - 15 4 Requires multivariable dynamic model Tuning may be difficult Less transparent “Everything goes down at the same time”

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Case studies 15 5

Step 7. Optimization layer (RTO) • Purpose: Identify active constraints and compute optimal setpoints (to be implemented by supervisory control layer) • Main structural issue: Do we need RTO? (or is process selfoptimizing) • RTO not needed when – Can “easily” identify change in active constraints (operating region) – For each operating region there exists self-optimizing var 15 6

Outline • Control structure design (plantwide control) • A procedure for control structure design I Top Down • • Step 1: Degrees of freedom Step 2: Operational objectives (optimal operation) Step 3: What to control ? (self-optimizing control) Step 4: Where set production rate? II Bottom Up • Step 5: Regulatory control: What more to control ? • Step 6: Supervisory control • Step 7: Real-time optimization • Conclusion / References 15 7

Summary: Main steps 1. What should we control (y 1=c=z)? • Must define optimal operation! 2. Where should we set the production rate? • At bottleneck 3. What more should we control (y 2)? • Variables that “stabilize” the plant 4. Control of primary variables • • 15 8 Decentralized? Multivariable (MPC)?

Conclusion Procedure plantwide control: I. Top-down analysis to identify degrees of freedom and primary controlled variables (look for self-optimizing variables) II. Bottom-up analysis to determine secondary controlled variables and structure of control system (pairing). 15 9

References • • • Halvorsen, I. J, Skogestad, S. , Morud, J. C. , Alstad, V. (2003), “Optimal selection of controlled variables”, Ind. Eng. Chem. Res. , 42, 3273 -3284. Larsson, T. and S. Skogestad (2000), “Plantwide control: A review and a new design procedure”, Modeling, Identification and Control, 21, 209 -240. Larsson, T. , K. Hestetun, E. Hovland S. Skogestad (2001), “Self-optimizing control of a large-scale plant: The Tennessee Eastman process’’, Ind. Eng. Chem. Res. , 40, 4889 -4901. Larsson, T. , M. S. Govatsmark, S. Skogestad and C. C. Yu (2003), “Control of reactor, separator and recycle process’’, Ind. Eng. Chem. Res. , 42, 1225 -1234 Skogestad, S. and Postlethwaite, I. (1996), Multivariable feedback control, Wiley • Skogestad, S. (2000). “Plantwide control: The search for the self-optimizing control structure”. J. Proc. Control 10, 487 -507. • Skogestad, S. (2003), ”Simple analytic rules for model reduction and PID controller tuning”, J. Proc. Control, 13, 291 -309. • Skogestad, S. (2004), “Control structure design for complete chemical plants”, Computers and Chemical Engineering, 28, 219 -234. (Special issue from ESCAPE’ 12 Symposium, Haag, May 2002). … + more…. . • See home page of S. Skogestad: 16 0 http: //www. chembio. ntnu. no/users/skoge/