Practical plantwide process control PID tuning Sigurd Skogestad

Practical plantwide process control: PID tuning Sigurd Skogestad, NTNU Thailand, April 2014

Part 2: PID tuning Part 2 (4 h). PID controller tuning: It pays off to be systematic! n 1. Obtaining first-order plus delay models q q q Open-loop step response From detailed model (half rule) From closed-loop setpoint response n 2. Derivation SIMC PID tuning rules q Controller gain, Integral time, derivative time n 3. Special topics q q q Integrating processes (level control) Other special processes and examples When do we need derivative action? Near-optimality of SIMC PID tuning rules Non PID-control: Is there an advantage in using Smith Predictor? (No) n. Examples

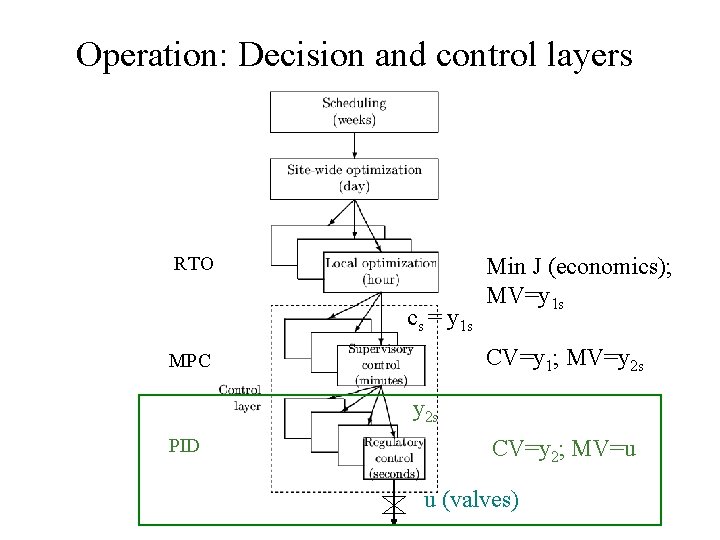
Operation: Decision and control layers RTO cs = y 1 s Min J (economics); MV=y 1 s CV=y 1; MV=y 2 s MPC y 2 s PID CV=y 2; MV=u u (valves)

PID controller e n Time domain (“ideal” PID) n Laplace domain (“ideal”/”parallel” form) n For our purposes. Simpler with cascade form n Usually τD=0. Then the two forms are identical. Only two parameters left (Kc and τI) How difficult can it be to tune? ? ? n n q Surprisingly difficult without systematic approach!

Trans. ASME, 64, 759 -768 (Nov. 1942). Disadvantages Ziegler-Nichols: 1. Aggressive settings 2. No tuning parameter 3. Poor for processes with large time delay (µ) Comment: Similar to SIMC for integrating process with ¿c=0: Kc = 1/k’ 1/µ ¿I = 4 µ

Disadvantage IMC-PID (=Lambda tuning): 1. Many rules 2. Poor disturbance response for «slow» processes (with large ¿ 1/µ)

Motivation for developing SIMC PID tuning rules 1. 2. 3. The tuning rules should be well motivated, and preferably be model-based analytically derived. They should be simple and easy to memorize. They should work well on a wide range of processes.

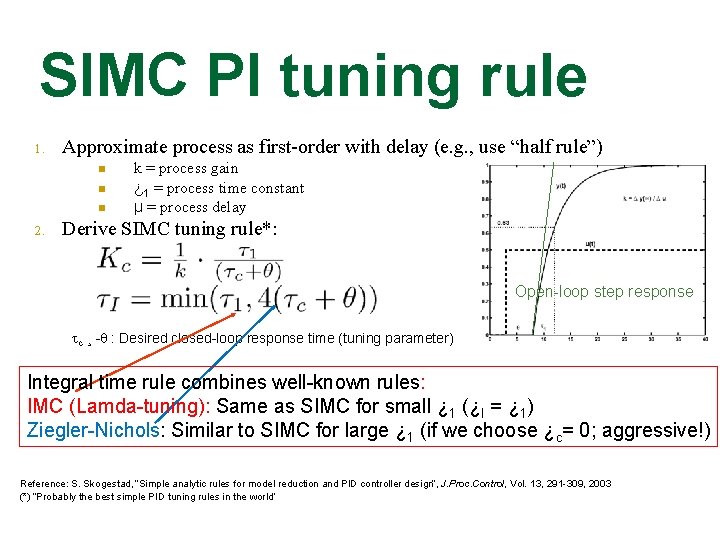
SIMC PI tuning rule 1. Approximate process as first-order with delay (e. g. , use “half rule”) n n n 2. k = process gain ¿ 1 = process time constant µ = process delay Derive SIMC tuning rule*: Open-loop step response c ¸ - : Desired closed-loop response time (tuning parameter) Integral time rule combines well-known rules: IMC (Lamda-tuning): Same as SIMC for small ¿ 1 (¿I = ¿ 1) Ziegler-Nichols: Similar to SIMC for large ¿ 1 (if we choose ¿c= 0; aggressive!) Reference: S. Skogestad, “Simple analytic rules for model reduction and PID controller design”, J. Proc. Control, Vol. 13, 291 -309, 2003 (*) “Probably the best simple PID tuning rules in the world”

MODEL Need a model for tuning n Model: Dynamic effect of change in input u (MV) on output y (CV) First-order + delay model for PI-control n Second-order model for PID-control n q Recommend: Use second-order model only if ¿ 2>µ

MODEL, Approach 1 A 1. Step response experiment n n Make step change in one u (MV) at a time Record the output (s) y (CV)

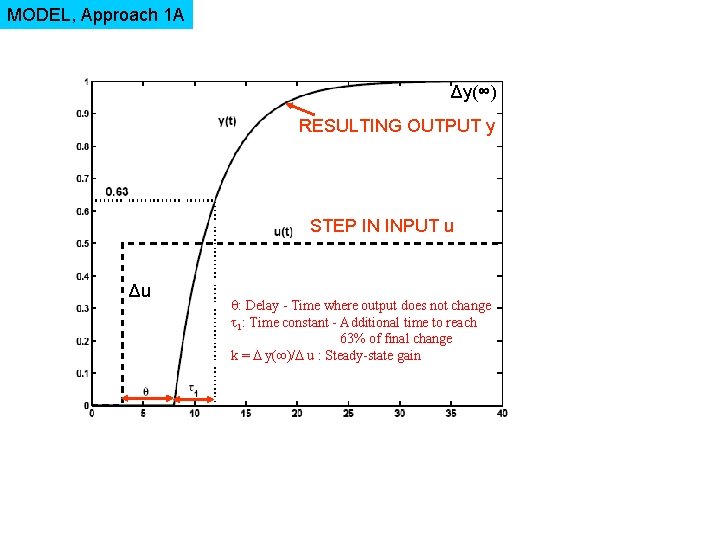
MODEL, Approach 1 A Δy(∞) RESULTING OUTPUT y STEP IN INPUT u Δu : Delay - Time where output does not change 1: Time constant - Additional time to reach 63% of final change k = y(∞)/ u : Steady-state gain

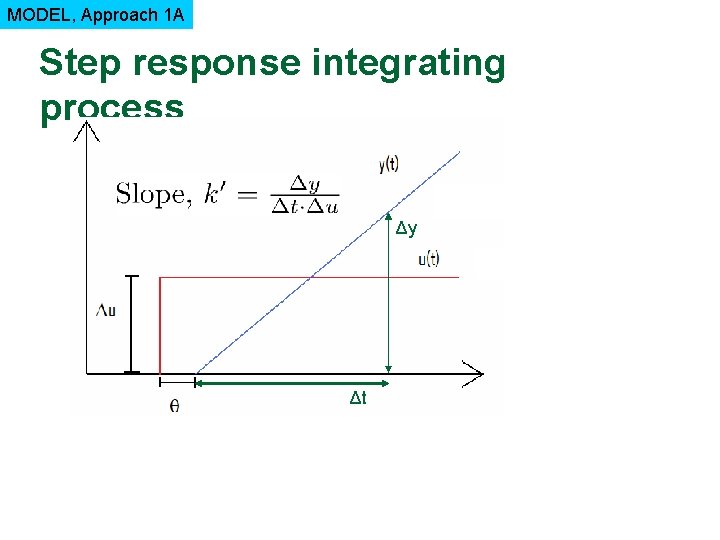
MODEL, Approach 1 A Step response integrating process Δy Δt

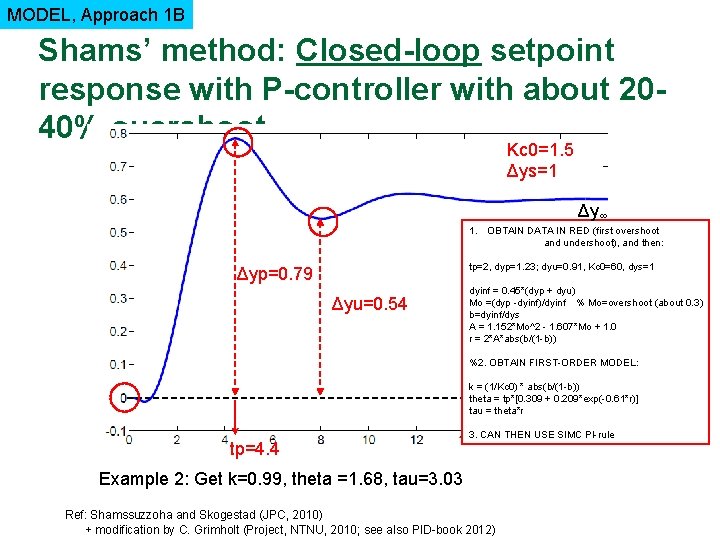
MODEL, Approach 1 B Shams’ method: Closed-loop setpoint response with P-controller with about 2040% overshoot Kc 0=1. 5 Δys=1 Δy∞ 1. OBTAIN DATA IN RED (first overshoot and undershoot), and then: tp=2, dyp=1. 23; dyu=0. 91, Kc 0=60, dys=1 Δyp=0. 79 Δyu=0. 54 dyinf = 0. 45*(dyp + dyu) Mo =(dyp -dyinf)/dyinf % Mo=overshoot (about 0. 3) b=dyinf/dys A = 1. 152*Mo^2 - 1. 607*Mo + 1. 0 r = 2*A*abs(b/(1 -b)) %2. OBTAIN FIRST-ORDER MODEL: k = (1/Kc 0) * abs(b/(1 -b)) theta = tp*[0. 309 + 0. 209*exp(-0. 61*r)] tau = theta*r tp=4. 4 3. CAN THEN USE SIMC PI-rule Example 2: Get k=0. 99, theta =1. 68, tau=3. 03 Ref: Shamssuzzoha and Skogestad (JPC, 2010) + modification by C. Grimholt (Project, NTNU, 2010; see also PID-book 2012)

MODEL, Approach 2 2. Model reduction of more complicated model n Start with complicated stable model on the form n Want to get a simplified model on the form n Most important parameter is the “effective” delay

MODEL, Approach 2

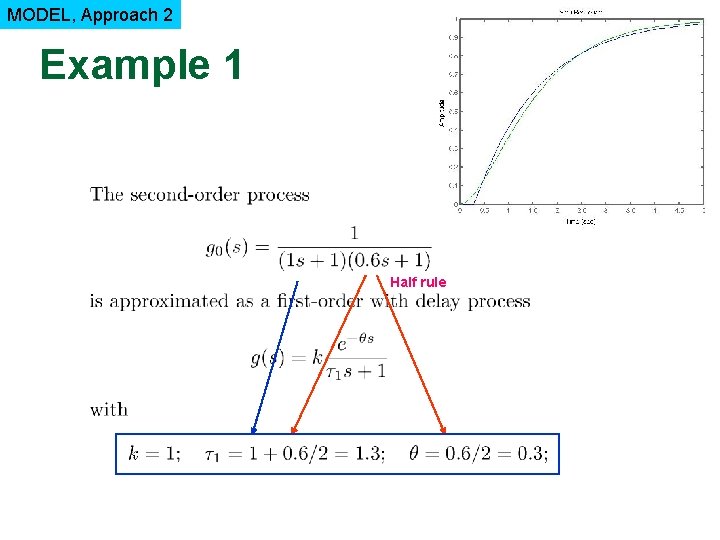
MODEL, Approach 2 Example 1 Half rule

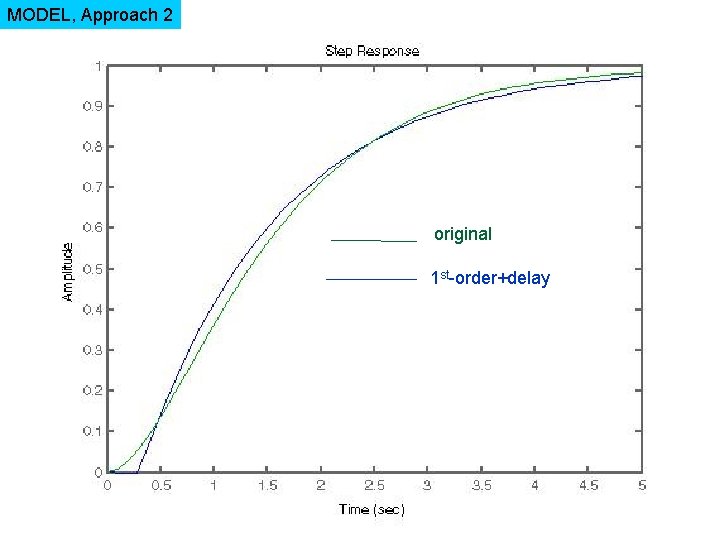
MODEL, Approach 2 original 1 st-order+delay

MODEL, Approach 2 2 half rule

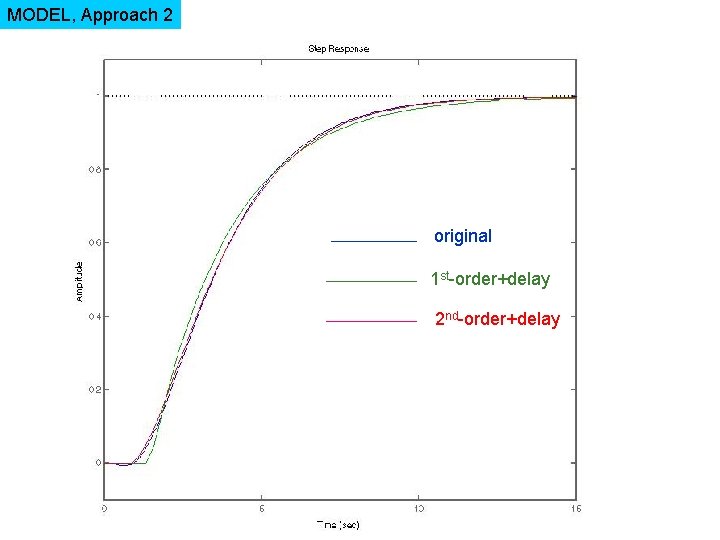
MODEL, Approach 2 original 1 st-order+delay 2 nd-order+delay

MODEL, Approach 2 Approximation of zeros c c c To make these rules more general (and not only applicable to the choice c= ): Replace (time delay) by c (desired closed-loop response time). (6 places) c Alternative and improved method forf approximating zeros: Simple Analytic PID Controller Tuning Rules Revisited J Lee, W Cho, TF Edgar - Industrial & Engineering Chemistry Research 2014, 53 (13), pp 5038– 5047

SIMC-tunings Derivation of SIMC-PID tuning rules n PI-controller (based on first-order model) n For second-order model add D-action. For our purposes, simplest with the “series” (cascade) PID-form:

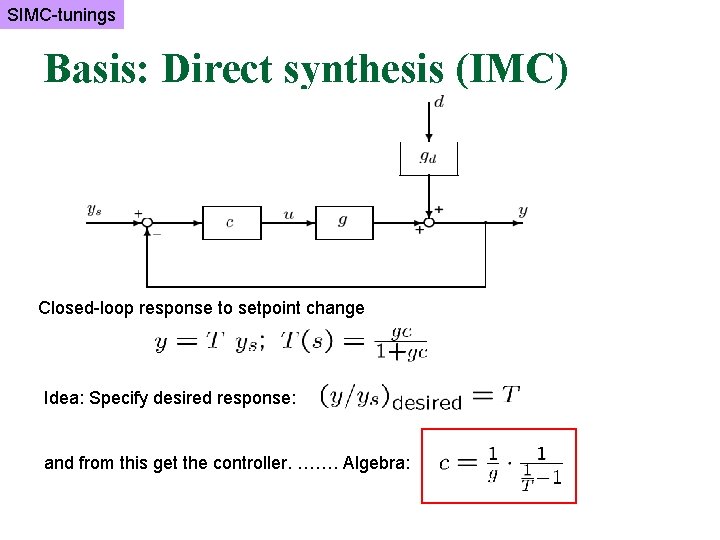
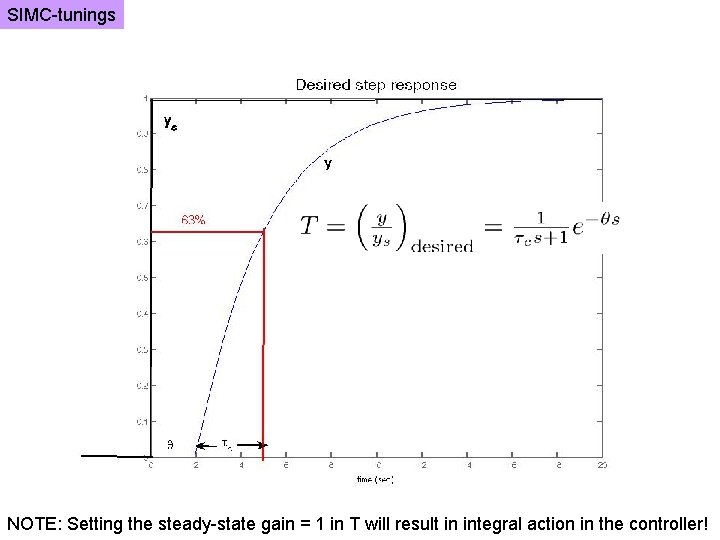
SIMC-tunings Basis: Direct synthesis (IMC) Closed-loop response to setpoint change Idea: Specify desired response: and from this get the controller. ……. Algebra:

SIMC-tunings NOTE: Setting the steady-state gain = 1 in T will result in integral action in the controller!

SIMC-tunings IMC Tuning = Direct Algebra: Synthesis

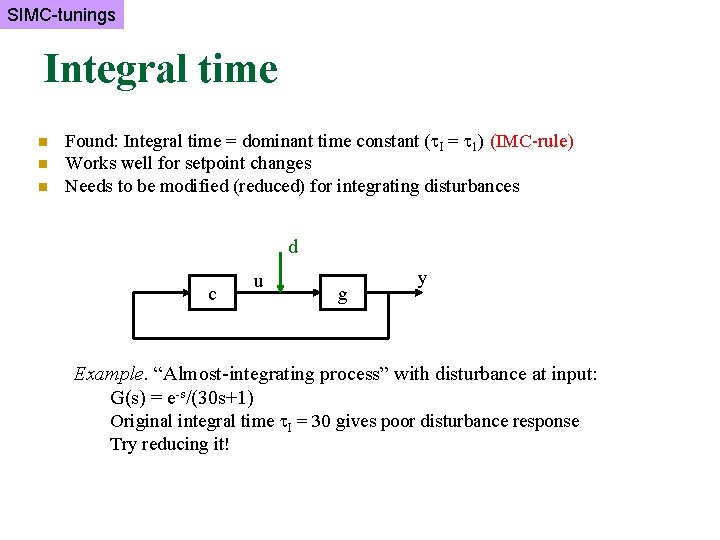
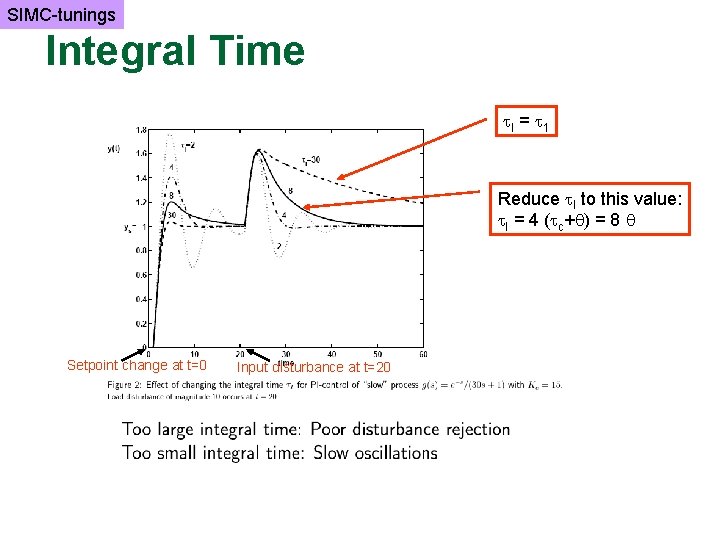
SIMC-tunings Integral time n n n Found: Integral time = dominant time constant ( I = 1) (IMC-rule) Works well for setpoint changes Needs to be modified (reduced) for integrating disturbances d c u g y Example. “Almost-integrating process” with disturbance at input: G(s) = e-s/(30 s+1) Original integral time I = 30 gives poor disturbance response Try reducing it!

SIMC-tunings Integral Time I = 1 Reduce I to this value: I = 4 ( c+ ) = 8 Setpoint change at t=0 Input disturbance at t=20

SIMC-tunings Integral time n Want to reduce the integral time for “integrating” processes, but to avoid “slow oscillations” we must require: n Derivation: n Setpoint response: Improve (get rid of overshoot) by “prefiltering”, y’s = f(s) ys. Details: See www. ntnu. no/users/skoge/publications/2003/tuning. PID Remark 13 II

SIMC-tunings Conclusion: SIMC-PID Tuning Rules One tuning parameter: c

SIMC-tunings Some insights from tuning rules 1. 2. 3. 4. The effective delay θ (which limits the achievable closedloop time constant τc) is independent of the dominant process time constant τ1! n It depends on τ2/2 (PI) or τ3/2 (PID) Use (close to) P-control for integrating process n Beware of large I-action (small τI) for level control Use (close to) I-control for fast process (with small time constant τ1) Parameter variations: For robustness tune at operating point with maximum value of k’ θ = (k/τ1)θ

Cascade PID -> Ideal PID

SIMC-tunings

SIMC-tunings Selection of tuning parameter c Two main cases 1. TIGHT CONTROL: Want “fastest possible TIGHT CONTROL: control” subject to having good robustness • 2. SMOOTH CONTROL: Want “slowest possible SMOOTH CONTROL: control” subject to acceptable disturbance rejection • • Want tight control of active constraints (“squeeze and shift”) Want smooth control if fast setpoint tracking is not required, for example, levels and unconstrained (“self-optimizing”) variables THERE ALSO OTHER ISSUES: Input saturation etc.

TIGHT CONTROL

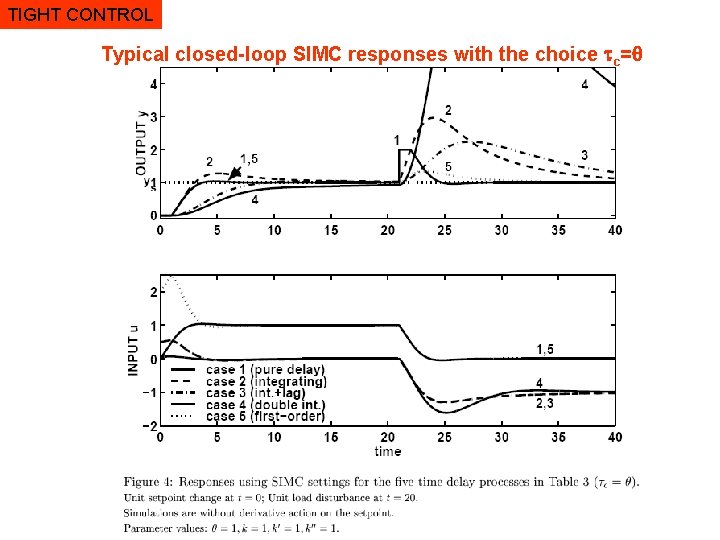
TIGHT CONTROL Typical closed-loop SIMC responses with the choice c=

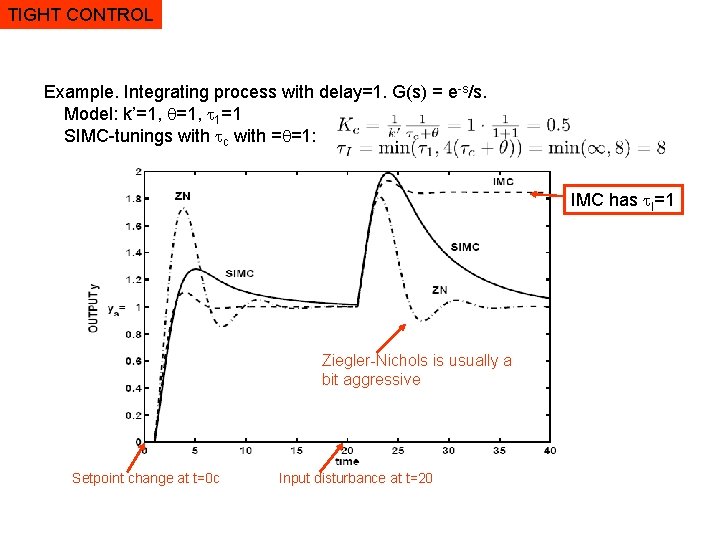
TIGHT CONTROL Example. Integrating process with delay=1. G(s) = e-s/s. Model: k’=1, 1=1 SIMC-tunings with c with = =1: IMC has I=1 Ziegler-Nichols is usually a bit aggressive Setpoint change at t=0 c Input disturbance at t=20

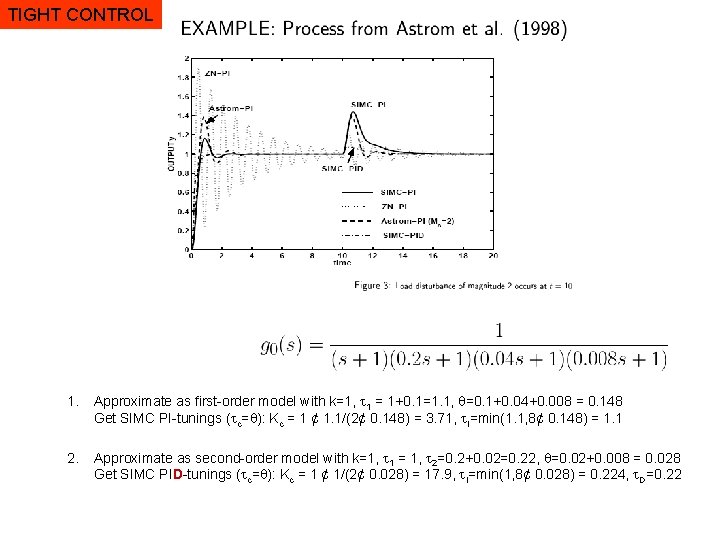
TIGHT CONTROL 1. Approximate as first-order model with k=1, 1 = 1+0. 1=1. 1, =0. 1+0. 04+0. 008 = 0. 148 Get SIMC PI-tunings ( c= ): Kc = 1 ¢ 1. 1/(2¢ 0. 148) = 3. 71, I=min(1. 1, 8¢ 0. 148) = 1. 1 2. Approximate as second-order model with k=1, 1 = 1, 2=0. 2+0. 02=0. 22, =0. 02+0. 008 = 0. 028 Get SIMC PID-tunings ( c= ): Kc = 1 ¢ 1/(2¢ 0. 028) = 17. 9, I=min(1, 8¢ 0. 028) = 0. 224, D=0. 22

SMOOTH CONTROL Tuning for smooth control n Tuning parameter: c = desired closed-loop response time n Selecting c= (“tight control”) is reasonable for cases with a relatively large effective delay n Other cases: Select c > for q q slower control smoother input usage n q q n less disturbing effect on rest of the plant less sensitivity to measurement noise better robustness Question: Given that we require some disturbance rejection. q q What is the largest possible value for c ? Or equivalently: The smallest possible value for Kc? Will derive Kc, min. From this we can get c, max using SIMC tuning rule S. Skogestad, ``Tuning for smooth PID control with acceptable disturbance rejection'', Ind. Eng. Chem. Res, 45 (23), 7817 -7822 (2006).

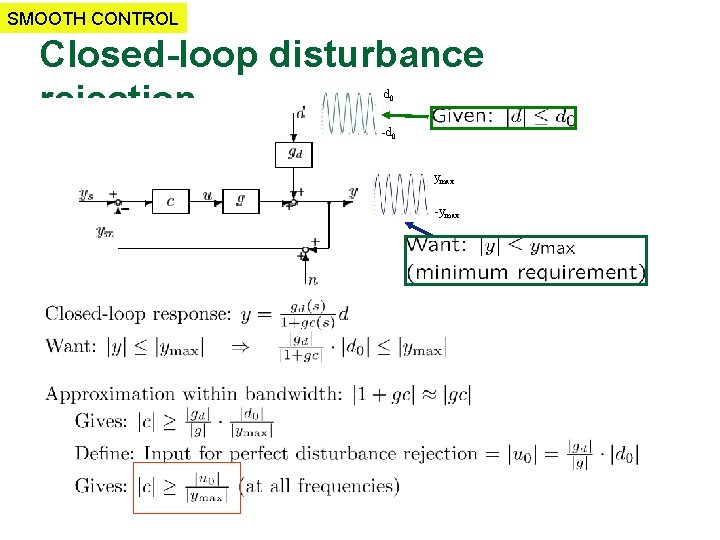
SMOOTH CONTROL Closed-loop disturbance rejection d 0 -d 0 ymax -ymax

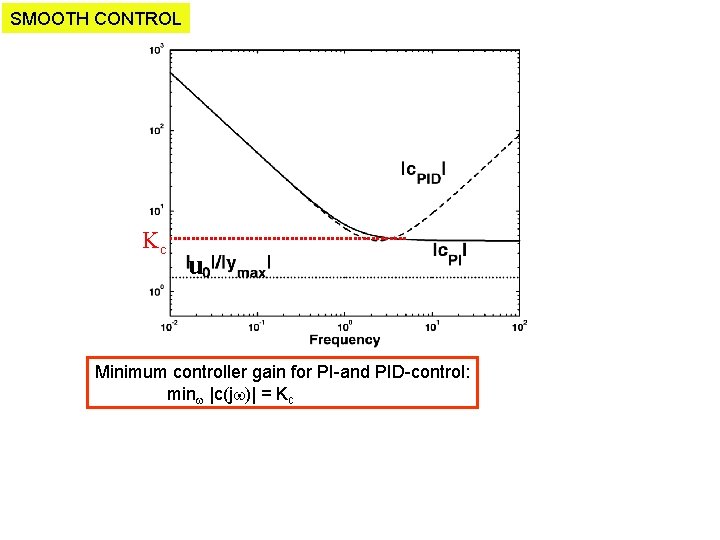
SMOOTH CONTROL Kc u Minimum controller gain for PI-and PID-control: min |c(j )| = Kc

SMOOTH CONTROL Rule: Min. controller gain for acceptable disturbance rejection: Kc ¸ |u 0|/|ymax| often ~1 (in span-scaled variables) |ymax| = allowed deviation for output (CV) |u 0| = required change in input (MV) for disturbance rejection (steady state) = observed change (movement) in input from historical data

SMOOTH CONTROL Rule: Kc ¸ |u 0|/|ymax| n Exception to rule: Can have lower Kc if disturbances are handled by the integral action. q q Disturbances must occur at a frequency lower than 1/ I Applies to: Process with short time constant ( 1 is small) and no delay ( ¼ 0). n q For example, flow control Then I = 1 is small so integral action is “large”

SMOOTH CONTROL Summary: Tuning of easy loops n Easy loops: Small effective delay ( ¼ 0), so closedn n loop response time c (>> ) is selected for “smooth control” ASSUME VARIABLES HAVE BEEN SCALED WITH RESPECT TO THEIR SPAN SO THAT |u 0/ymax| = 1 (approx. ). Flow control: Kc=0. 2, I = 1 = time constant valve (typically, 2 to 10 s; close to pure integrating!) Level control: Kc=2 (and no integral action) Other easy loops (e. g. pressure): Kc = 2, I = min(4 c, 1) q Note: Often want a tight pressure control loop (so may have Kc=10 or larger)

Conclusion PID tuning 3. Derivative time: Only for dominant second-order processes

PID: More (Special topics) 1. 2. 3. 4. 5. Integrating processes (level control) Other special processes and examples When do we need derivative action? Near-optimality of SIMC PID tuning rules Non PID-control: Is there an advantage in using Smith Predictor? (No) April 4 -8, 2004 KFUPM-Distillation Control Course 46

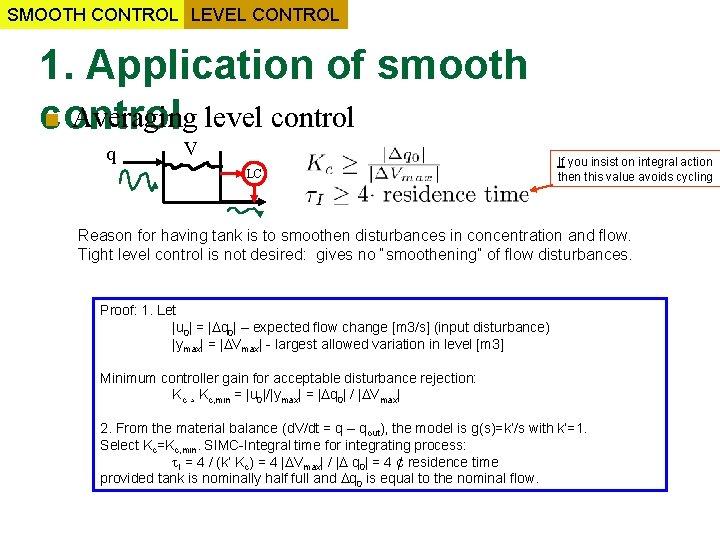
SMOOTH CONTROL LEVEL CONTROL 1. Application of smooth n Averaging level control q V LC If you insist on integral action then this value avoids cycling Reason for having tank is to smoothen disturbances in concentration and flow. Tight level control is not desired: gives no “smoothening” of flow disturbances. Proof: 1. Let |u 0| = | q 0| – expected flow change [m 3/s] (input disturbance) |ymax| = | Vmax| - largest allowed variation in level [m 3] Minimum controller gain for acceptable disturbance rejection: Kc ¸ Kc, min = |u 0|/|ymax| = | q 0| / | Vmax| 2. From the material balance (d. V/dt = q – qout), the model is g(s)=k’/s with k’=1. Select Kc=Kc, min. SIMC-Integral time for integrating process: I = 4 / (k’ Kc) = 4 | Vmax| / | q 0| = 4 ¢ residence time provided tank is nominally half full and q 0 is equal to the nominal flow.

LEVEL CONTROL More on level control n n Level control often causes problems Typical story: q q n n Level loop starts oscillating Operator detunes by decreasing controller gain Level loop oscillates even more. . . ? ? ? Explanation: Level is by itself unstable and requires control.

LEVEL CONTROL How avoid oscillating levels? 0. 1 ¼ 1/ 2

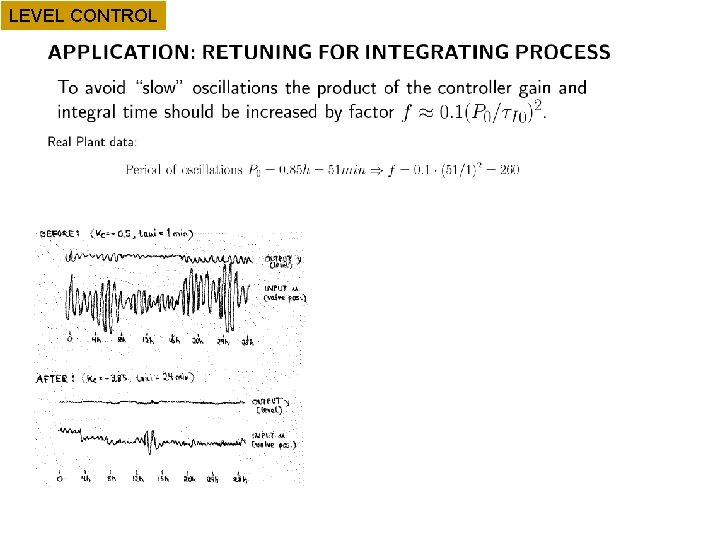
LEVEL CONTROL Case study oscillating level n n n We were called upon to solve a problem with oscillations in a distillation column Closer analysis: Problem was oscillating reboiler level in upstream column Use of Sigurd’s rule solved the problem

LEVEL CONTROL

SIMC-tunings 2. Some special cases One tuning parameter: c

SIMC-tunings Another special case: IPZ process n IPZ-process may represent response from steam flow to pressure n Rule T 2: SIMC-tunings n These tunings turn out to be almost identical to the tunings given on page 104 -106 in the Ph. D. thesis by O. Slatteke, Lund Univ. , 2006 and K. Forsman, "Reglerteknik for processindustrien", Studentlitteratur, 2005.

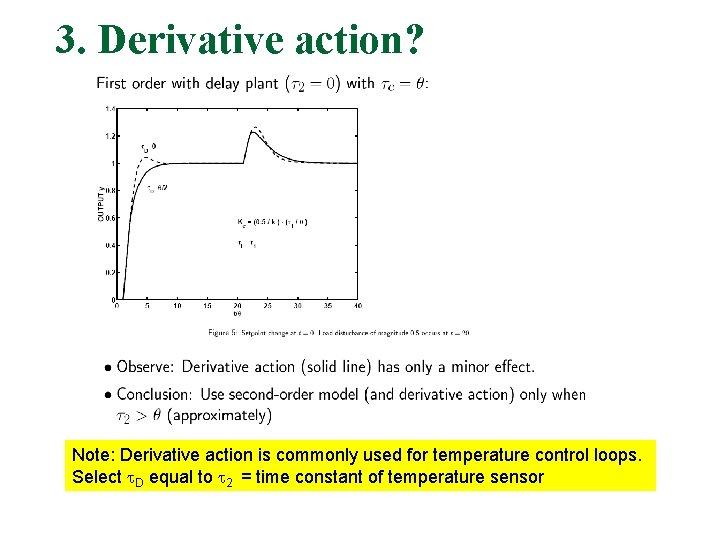
3. Derivative action? Note: Derivative action is commonly used for temperature control loops. Select D equal to 2 = time constant of temperature sensor

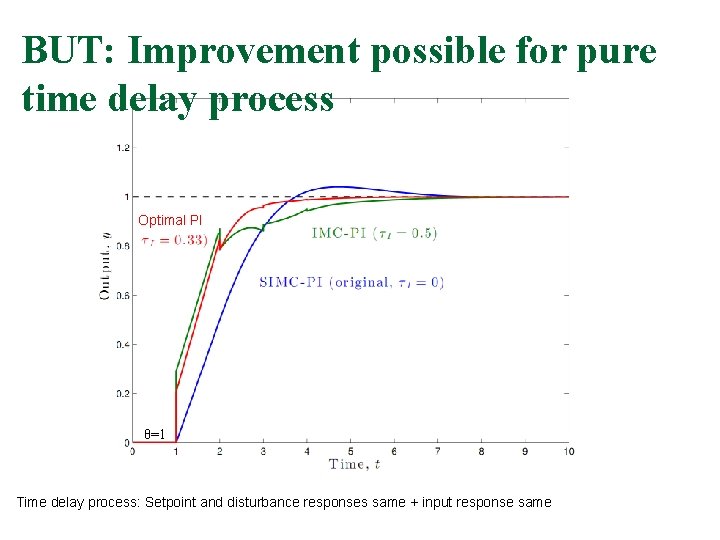
BUT: Improvement possible for pure time delay process Optimal PI θ=1 Time delay process: Setpoint and disturbance responses same + input response same

Pure time delay process

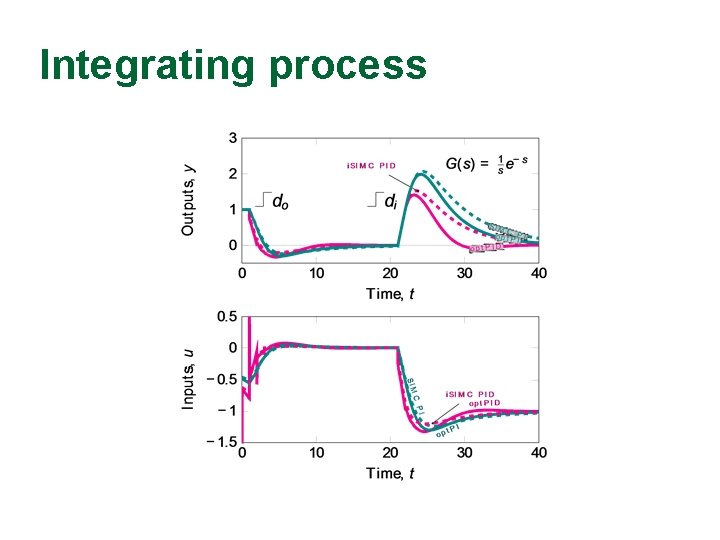
Two “Improved SIMC”-rules that give optimal for pure time delay process 1. Improved PI-rule (i. SIMC PI): Add θ/3 to 1 2. Improved PID-rule (i. SIMC PID): Add θ/3 to 2 i. SIMC PID is better for integrating process

Integrating process

4. Optimality of SIMC rules How good are the SIMC-rules compared to optimal PI/PID? n Multiobjective. Tradeoff between q q Output performance Robustness Input usage Noise sensitivity High controller gain (“tight control”) Low controller gain (“smooth control”) • Quantification – Output performance: • Rise time, overshoot, settling time • IAE or ISE for setpoint/disturbance – Robustness: Ms, Mt, GM, PM, Delay margin, … – Input usage: ||KSGd||, TV(u) for step response – Noise sensitivity: ||KS||, etc. Our choice: J = avg. IAE for setpoint/disturbance Ms = peak sensitivity

Performance (J):

Robustness (Ms):

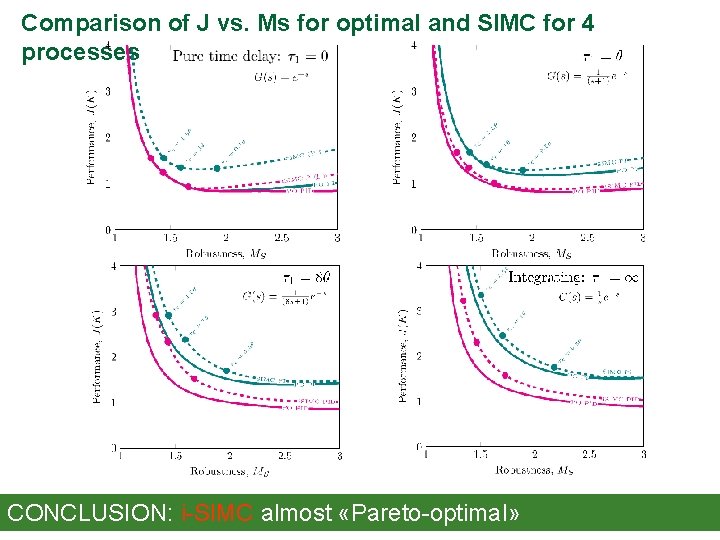
Comparison of J vs. Ms for optimal and SIMC for 4 processes CONCLUSION: i-SIMC almost «Pareto-optimal»

5. Better with IMC, Smith Predictor or MPC? n n Suprisingly, the answer is: NO, worse

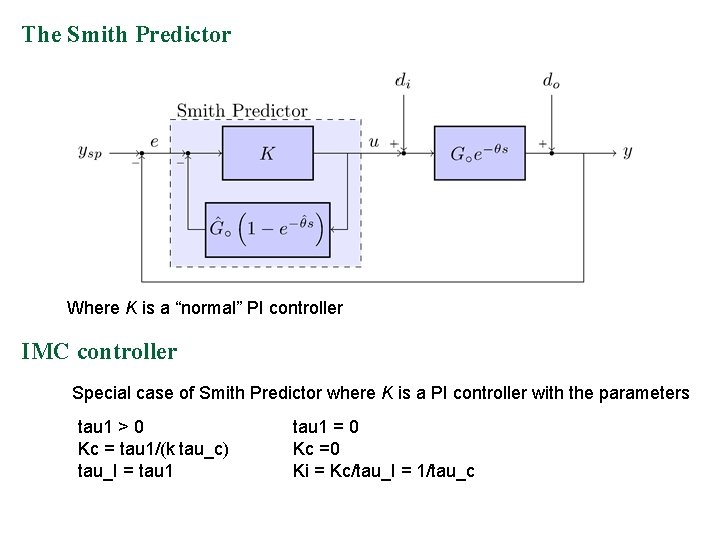
The Smith Predictor Where K is a “normal” PI controller IMC controller Special case of Smith Predictor where K is a PI controller with the parameters tau 1 > 0 Kc = tau 1/(k tau_c) tau_I = tau 1 = 0 Kc =0 Ki = Kc/tau_I = 1/tau_c

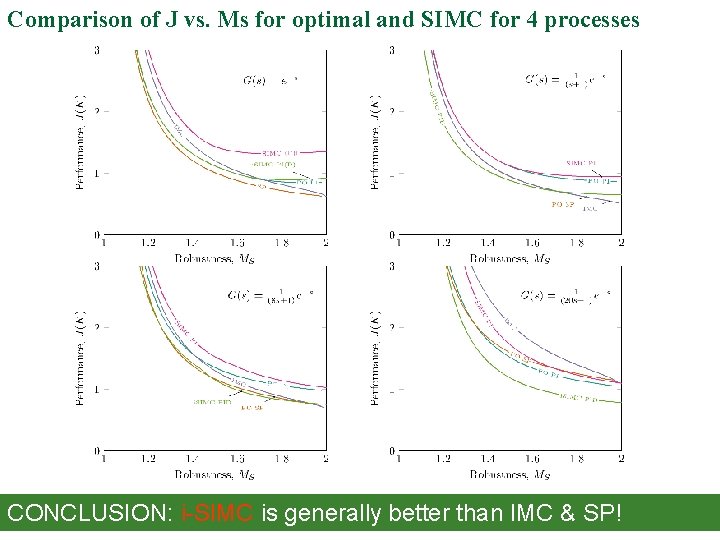
Comparison of J vs. Ms for optimal and SIMC for 4 processes CONCLUSION: i-SIMC is generally better than IMC & SP!

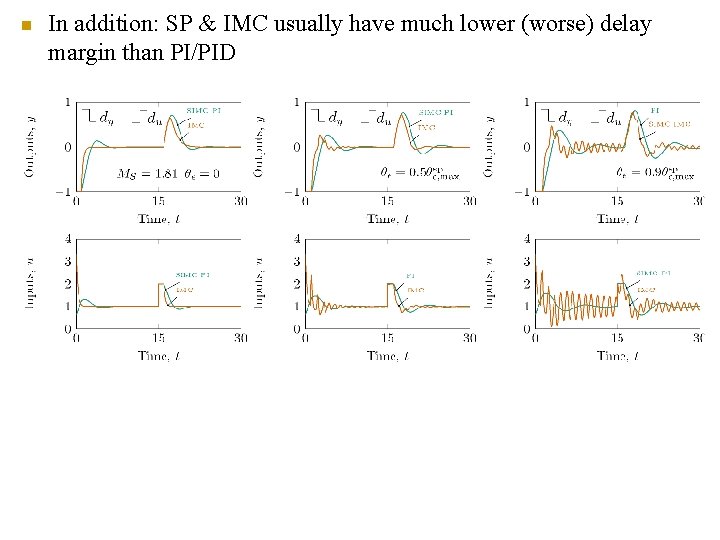
n In addition: SP & IMC usually have much lower (worse) delay margin than PI/PID

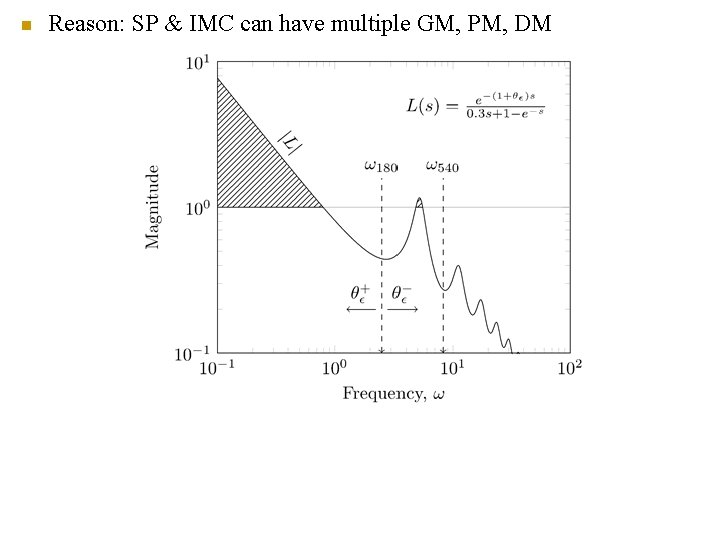
n Reason: SP & IMC can have multiple GM, PM, DM

n CONCLUSION n Well-tuned PI or PID is better than Smith Predictor or IMC!! Especially for integrating processes n