MAT 102 FUNKSJONER 3 April PLAN FOR DAGEN

MAT 102 FUNKSJONER 3 April

PLAN FOR DAGEN • Introduksjon til funksjoner • Funksjonsdidaktikk • Lineære funksjoner

HVA ER EN FUNKSJON?

HVA ER EN FUNKSJON?

HVA ER EN FUNKSJON? Omtrent alle situasjoner i hverdagslivet kan beskrives ved hjelp av en funksjon. F. eks pris vi må betale for appelsiner som koster 14, 30 pr kg Hvor mye penger vi har på sparekonto i banken i tiden etter at vi satte inn 1000 kr Hvor lang tid vi bruker på å kjøre fra et sted til et annet Arealet til gressplener Hvor mye vi tjener pr måned, og hvor mye skatt vi må betale Hvor mye hostesaft barnet vårt skal ha pr gang Hvor mye hundemat hunden skal ha pr dag Temperaturmåling på gitte tidspunkter

HVA ER EN FUNKSJON? La oss tenke oss en liten tunnel som det går an å kjøre en bil gjennom. Hver gang en rød bil kjører inn i tunnelen er den blå når den kommer ut. Når en svart bil kjører inn er den blå når den kommer ut. Når en grønn bil kjører inn er den blå når den kommer ut. Når en blå bil kjører inn er den blå når den kommer ut. Hva er tunnelens funksjon?

FUNKSJONSBOKSEN

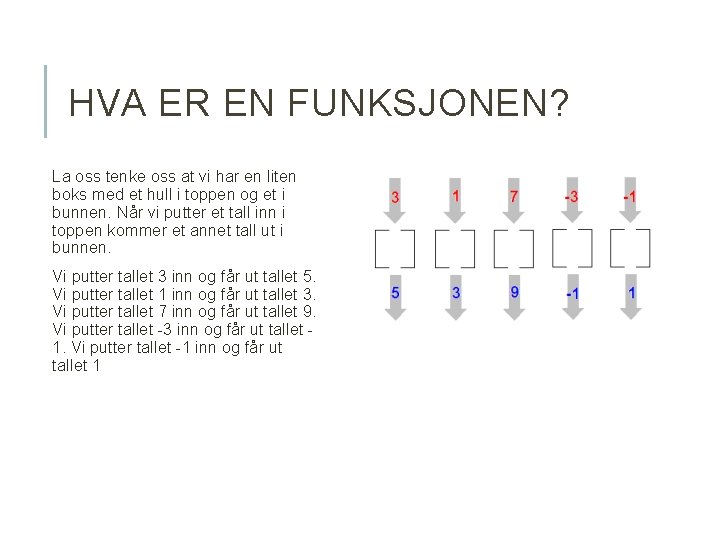
HVA ER EN FUNKSJONEN? La oss tenke oss at vi har en liten boks med et hull i toppen og et i bunnen. Når vi putter et tall inn i toppen kommer et annet tall ut i bunnen. Vi putter tallet 3 inn og får ut tallet 5. Vi putter tallet 1 inn og får ut tallet 3. Vi putter tallet 7 inn og får ut tallet 9. Vi putter tallet -3 inn og får ut tallet 1. Vi putter tallet -1 inn og får ut tallet 1

FUNKSJONSUTRYKK / FUNSJONSFORSKRIFT

ALFA LÆREBOK

MENGDER Definisjonsmengden til en funksjon er mengden som består av de tallene eller verdiene hvor funksjonen er definert. Verdimengden til en funksjon er de mulige funksjonsverdiene som funksjonen kan ha

ENTYDIGHET

KONTINUERLIG/ DISKONTINUERLIG

OPPGAVE Beskriv en situasjon vi kan utrykke som en funksjon. Identifiser hva som er definisjonsmengde og hva som er verdimengden Er det en kontinuerlig eller diskontinuerlig?

FORSTÅ FUNKSJONSBEGREPET Hva må ligge av grunnleggende kunnskap for å utvikle og forstå funksjonsbegrepet?

FUNKSJONSDIDAKTIK K

MATEMATISK BEGREP Et matematikk begrep har ikke vokst fram isolert, men eksisterer i et nettverk av enkelte ideer. Vi kaller slike nettverk av ideer for begreps strukturer. For å gjøre nøyaktig greie for hva et matematisk begrep inneholder, og hvordan man kan tilrettelegge undervisningen, må man først avdekke begrepets struktur. Det vil si: hvordan dette begrepet er knyttet til andre begreper, og hvordan det blir brukt på ulike måter i praktiske situasjoner.

HVA ER DET SOM GJØR AT FUNKSJONER OPPFATTES SOM SÅ UTFORDRENDE FOR SÅ MANGE?

JANVIERS TABELL

FRA FORMEL TIL GRAF 24

FRA GRAF TIL SITUASJON 26

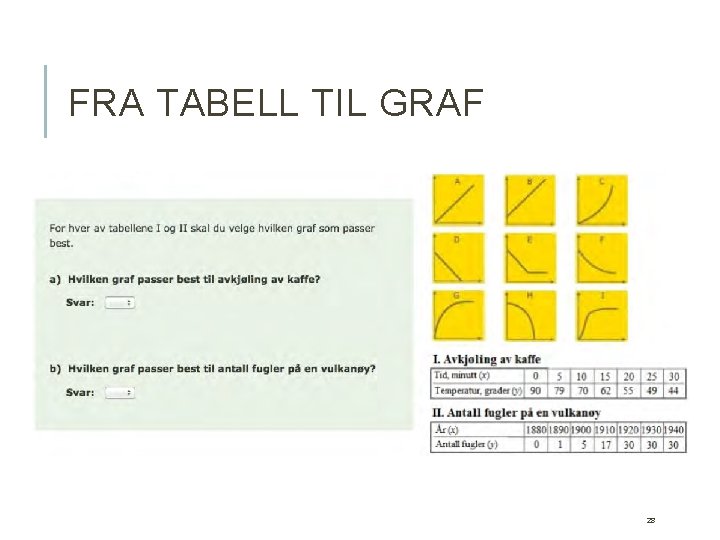
FRA TABELL TIL GRAF 28

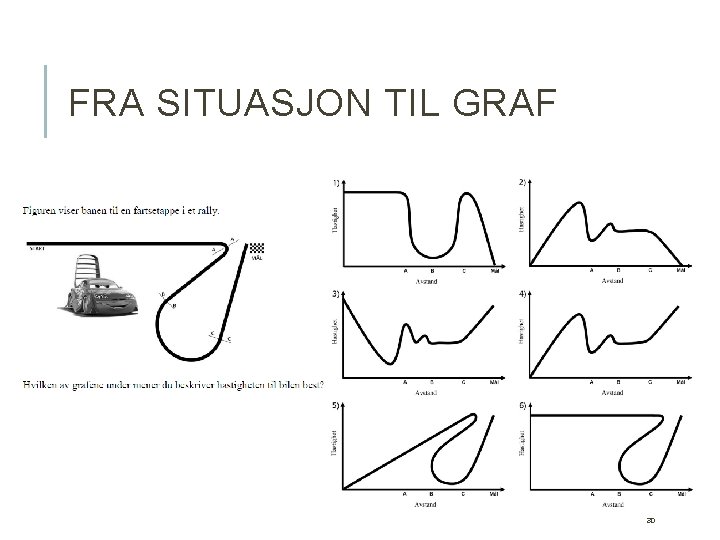
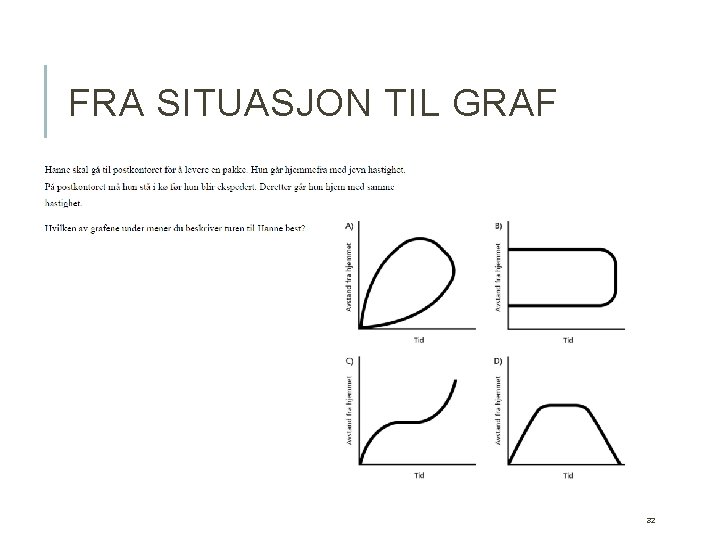
FRA SITUASJON TIL GRAF 30

FRA SITUASJON TIL GRAF 32

KOORDINATSYSTEMER

MOTIVASJON FOR Å JOBBE MED KOORDINATSYSTEMER Hvordan kan vi beskrive en plass i klasserommet? Hvordan kan vi forklare hvor en båt er på havet? Hvordan beskrive posisjonen til en løper på et sjakkbrett Hvordan er et regneark bygd opp? Kanskje elevene kan komme på flere eksempler?

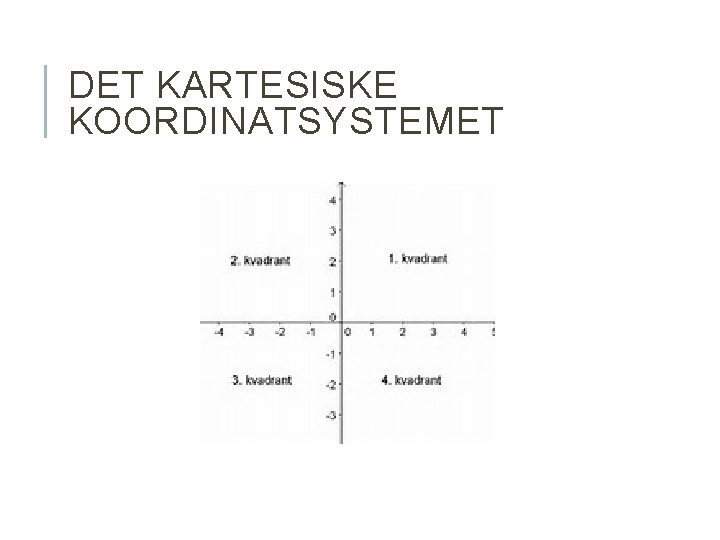
DET KARTESISKE KOORDINATSYSTEMET

KOORDINATSYSTEM Vi kan bestemme posisjonen til et punkt på en graf i forhold til et koordinatsystem. Et koordinatsystem har en vertikal akse som vi kaller y-aksen eller andreaksen. Og den har en horisontal akse som vi kaller x-aksen eller førsteaksen. Punktet der de møtes kalles origo.

PUNKT PÅ KOORDINATSYSTEM Koordinatene til et punkt er oppgitt som en x-koordinat og en y-koordinat. De oppgis i en parentes med x koordinaten først og deretter y koordinaten. Eksempler er: A=(2, 2) B=(-1, -3) C=(1, -2) D=(-2, 1) (x, y)

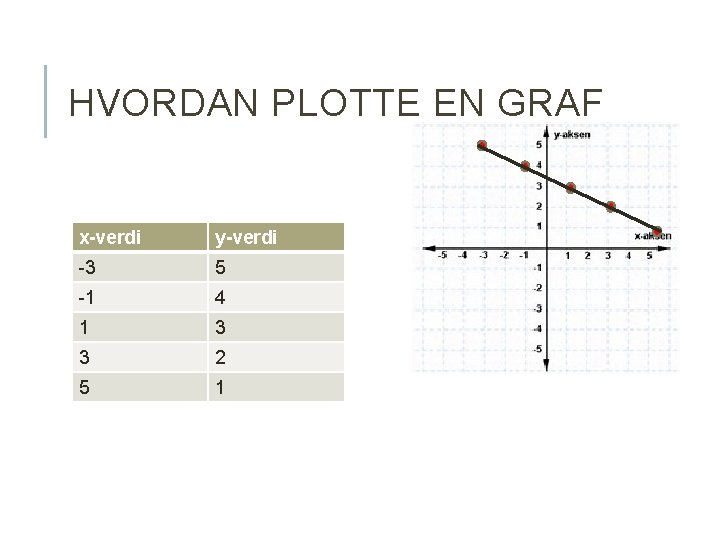
HVORDAN PLOTTE EN GRAF x-verdi y-verdi -3 5 -1 4 1 3 3 2 5 1

LINEÆRE FUNKSJONER

POLYNOMFUNKSJONER

HVA ER EN LINEÆR FUNKSJON? Følgende er eksempler på noe som ikke er en lineær funksjon: f(x) = x². Ser slik ut: Denne er ikke lineær. x = 2. Ser slik ut: Her er y ikke en funksjon av x.

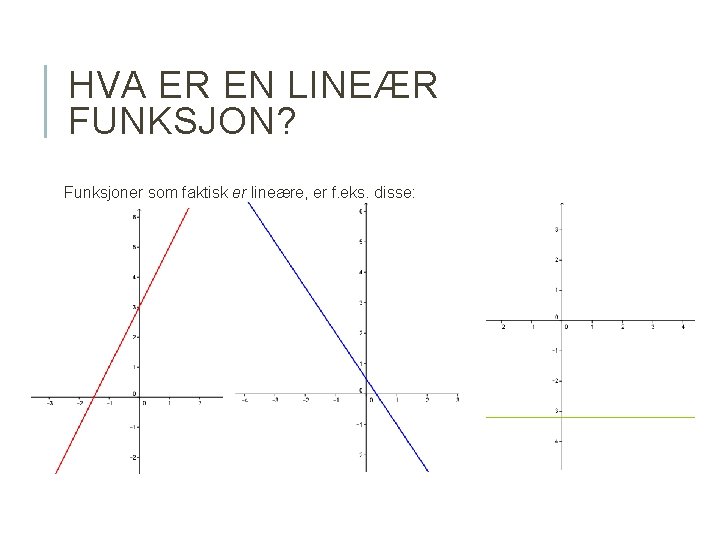
HVA ER EN LINEÆR FUNKSJON? Funksjoner som faktisk er lineære, er f. eks. disse: f(x) = 2 x + 3: g(x) = – 1, 5 x + 0, 5: h(x) = – 3, 2

PLOTTE EN LINEÆR FUNKSJON Hvor mange punkter trenger vi egentlig for å plotte en lineær funksjon?

FUNKSJONSUTRYKK

FUNKSJONSUTRYKKET TIL LINEÆRE FUNKSJONER.

HVA BESTEMMER FORMEN PÅ GRAFEN? Vi kan vise formelt hvordan b bestemmer hvor grafen skjærer y-aksen: Grafen skjærer y-aksen når x=0. Altså: Vi skal finne y-verdien når x=0. Vi setter inn: f(0) = a· 0 + b = b. Altså skjærer grafen y-aksen i b. Merk: Hvis b=0, da går grafen gjennom origo. Mange elever har misoppfatningen at alle grafer går gjennom origo. Det er mulig at dette har sammenheng med at proporsjonalitet innføres før funksjonsbegrepet.

HVA BESTEMMER FORMEN PÅ GRAFEN? Men hva forteller a oss? La oss ta utgangspunkt i et eksempel: Et (ganske gammeldags) mobilabonnement har en fastpris på 99 kr i måneden, og minuttprisen er 0, 30 kr. Hva kommer regningen på? r(t) = 0, 30 t + 99, der t er antall minutter. Grafen er som vist til høyre. Merk hvordan grafen skjærer y-aksen i 99. Det betyr at hvis vi ringer i 0 minutter, betaler vi 99 kr.

HVA BESTEMMER FORMEN PÅ GRAFEN? Men hvordan kan vi forstå 0, 30 i forhold til grafen? Jo, når vi ringer i ett minutt utover det vi allerede har ringt, da øker y med 0, 30. Dette kan vi se fra grafen til funksjonen. Figuren under er totalt ute av skala, merk det! Men ellers illustrerer den hvordan vi kan se hva y øker med hvis t øker med 1. I dette eksempelet kaller man derfor 0, 30 for stigningstallet til grafen. Stigningstallet er altså hvor mye y vokser hvis variabelen vokser med 1.

HVA BESTEMMER FORMEN PÅ GRAFEN? Her er et mer «vanlig» eksempel: y = 2 x + 3 Grafen er vist til høyre. Den røde trekanten markerer hvordan stigningstallet er definert ved å gå én bort og se hvor mange hakk vi må gå opp. Her er stigningstallet 2.

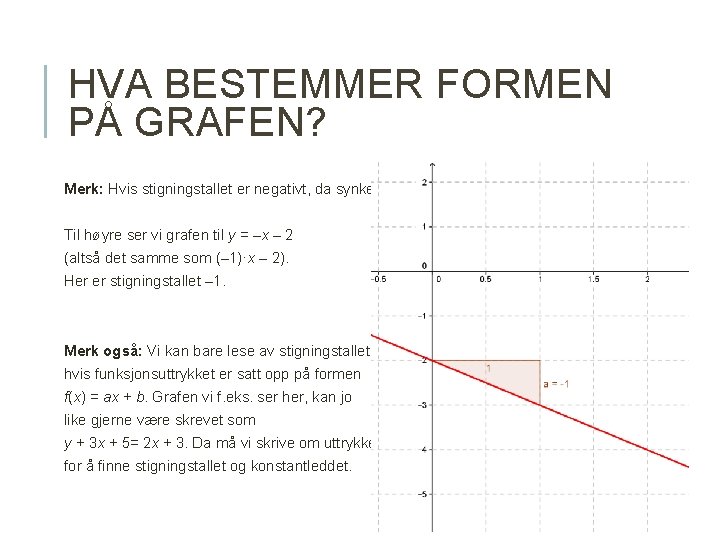
HVA BESTEMMER FORMEN PÅ GRAFEN? Merk: Hvis stigningstallet er negativt, da synker grafen. Til høyre ser vi grafen til y = –x – 2 (altså det samme som (– 1)·x – 2). Her er stigningstallet – 1. Merk også: Vi kan bare lese av stigningstallet hvis funksjonsuttrykket er satt opp på formen f(x) = ax + b. Grafen vi f. eks. ser her, kan jo like gjerne være skrevet som y + 3 x + 5= 2 x + 3. Da må vi skrive om uttrykket for å finne stigningstallet og konstantleddet.

MER OM STIGNINGSTALL

ULIKE STIGNINGSTALL

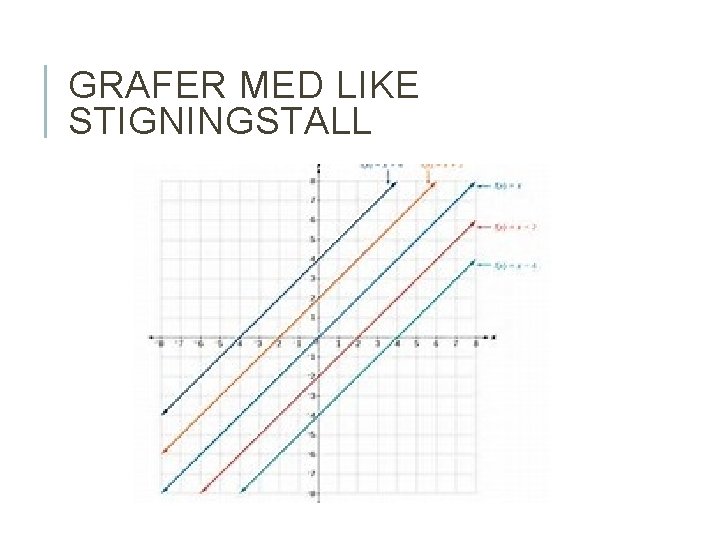
GRAFER MED LIKE STIGNINGSTALL

STIGNINGSTALL

FINN STIGNINGSTALLET Finn stigningstallet til linjen mellom punktparene: (2, 3) og (4, 5) (1. 1) og (2, 4) (2. 1) og (5, -1)

OPPGAVER a) Lag tre eksempler på en lineær funksjon med stigningstall 4. Finnes det flere enn dette? b) Lag tre eksempler på en lineær funksjon med konstantledd 4. Finnes det flere enn dette?

Å FINNE LIKNINGEN

Å FINNE LIKNINGEN TIL EN FUNKSJON For å finne formelen til en lineær funksjon trenger vi minst en av følgende: 1. Stigningstall og et punkt på linja 2. To punkter på linja 3. Grafen

EKSEMPEL La oss si at vi har en lineær funksjon der stigningstallet er 5, og vi vet at funksjonen går gjennom punktet (4, 11). Hvordan skal vi finne en ligning til funksjonen?

ETTPUNKTSFORMELEN

OM STIGNINGSTALLET IKKE ER OPPGITT

EKSEMPEL La oss tenke oss at vi har en lineær funksjon der vi ikke kjenner til stigningstallet, men kjenner til to punkter, f. eks. (2, 7) og (6, 19). Vi skal finne ligningen til funksjonen.

TOPUNKTSFORMELEN

OPPGAVER

GRAFISK LØSNING AV LIKNINGSETT

TO LIKNINGER

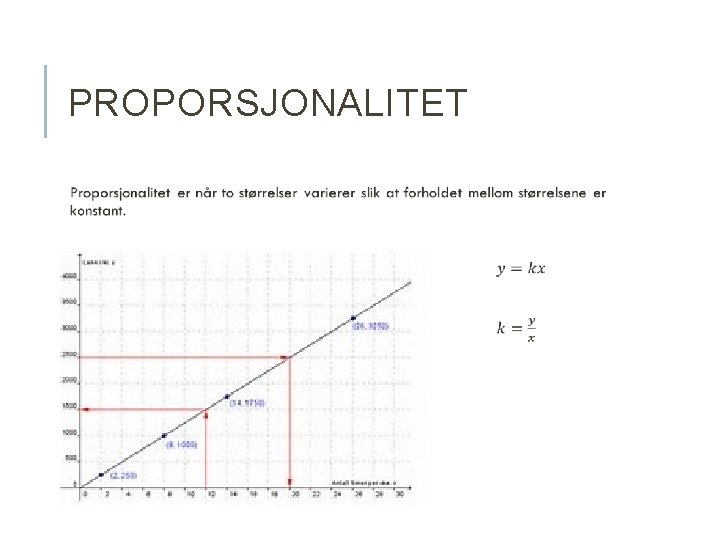
PROPORSJONALITET

PROPORSJONALITET

OPPGAVER Å GJØRE HJEMME

OPPGAVER Alfa, s. 299– 300 i utgave 1 / s. 335– 336 i utgave 2: Oppgave 4. 4, 4. 5, 4. 6, 4. 7, 4. 8. Alfa: 4. 9, 4. 10, 4. 11, 4. 12, 4. 13, 4. 14, 4. 15, 4. 16, 4. 17, 4. 21, 4. 22, 4. 23, 4. 24 (kan være litt utfordrende).