Kapitel 5 Der Algorithmus 1 Definieren Sie den

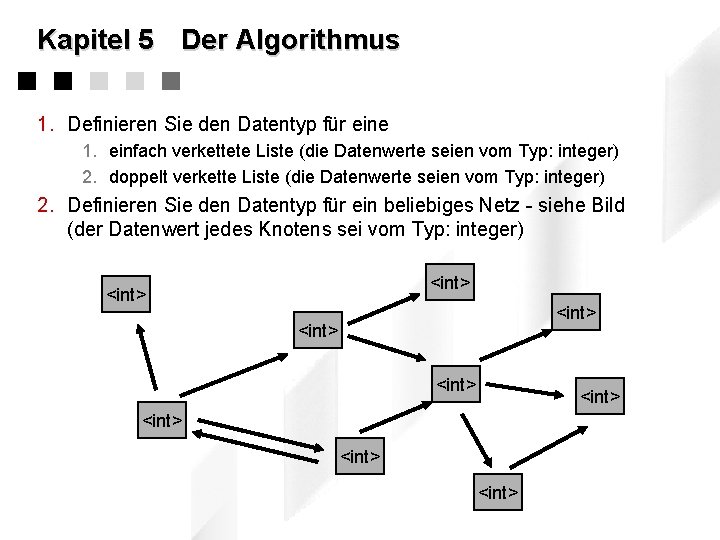
Kapitel 5 Der Algorithmus 1. Definieren Sie den Datentyp für eine 1. einfach verkettete Liste (die Datenwerte seien vom Typ: integer) 2. doppelt verkette Liste (die Datenwerte seien vom Typ: integer) 2. Definieren Sie den Datentyp für ein beliebiges Netz - siehe Bild (der Datenwert jedes Knotens sei vom Typ: integer) <int> <int> <int>

5. 1 Ein Beispiel n Zunächst soll ein kleines Beispiel in eine mögliche Aufgabenstellung aus dem (bekannten) Bereich der Mathematik einführen und dadurch auch eine (eingeschränkte) Vorstellung über die Aufgaben und Elemente eines Algorithmuses geben. n Inhalt 1. 2. 3. 4. 5. 6. 7. Das Problem (Beispiel) Ein Algorithmus II Vergleich der Algorithmen Ein Algorithmus III Fragestellungen Ein weiterer Algorithmus

5. 1. 1 Das Problem n Eine quadratischen Gleichung: x 2 + 8 x + 7 = 0 n Allgemeine Darstellung der quadratischen Gleichung x 2 + px + q = 0 n Allgemeine Lösung der quadratischen Gleichung x = -p/2 + p 2/4 - q - 1, 2 n Lösung der quadratischen Gleichung x = -8/2 + 82/4 - 7 - 1, 2 = -4 + - 3 x 1 = -1 x 2 = -7

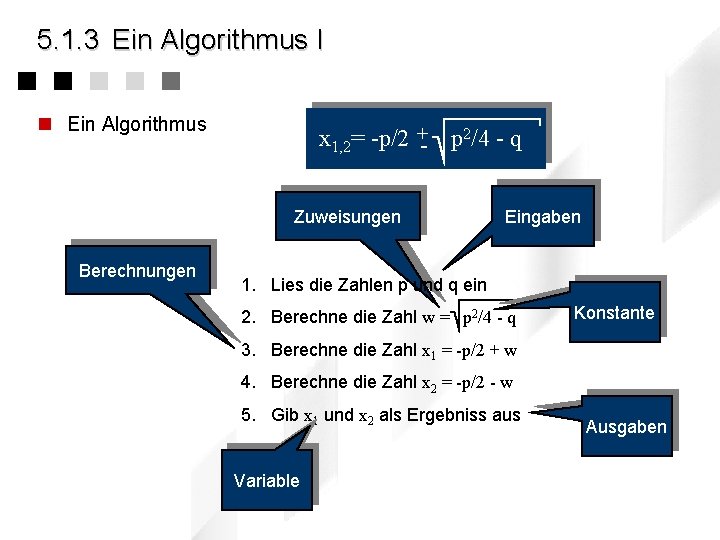
5. 1. 3 Ein Algorithmus I n Ein Algorithmus x 1, 2= -p/2 +- p 2/4 - q Zuweisungen Berechnungen Eingaben 1. Lies die Zahlen p und q ein 2. Berechne die Zahl w = p 2/4 - q Konstante 3. Berechne die Zahl x 1 = -p/2 + w 4. Berechne die Zahl x 2 = -p/2 - w 5. Gib x 1 und x 2 als Ergebniss aus Variable Ausgaben

5. 1. 4 Ein Algorithmus II n Ein zweiter Algorithmus 1. Lies die Zahlen p und q ein x 1, 2= -p/2 +- p 2/4 - q 2. Berechne die Zahl p/2; Nenne diese Zahl a 3. Berechne die Zahl a 2 ; Nenne diese Zahl b 4. Berechne die Zahl b-q ; Nenne diese Zahl c 5. Berechne die Zahl c ; Nenne diese Zahl d 6. Berechne die Zahl -a ; Nenne diese Zahl e 7. Berechne die Zahl e + d ; Nenne diese Zahl x 1 8. Berechne die Zahl e - d ; Nenne diese Zahl x 2 9. Gib x 1 und x 2 als Ergebniss aus FHSymbol 1 Es gibt (oft unendlich) viele Algorithmen zur Lösung eines Problems

5. 1. 5 Vergleich der Algorithmen Berechne die Zahl w = p 2/4 - q Berechne die Zahl p/2; Nenne diese Zahl a Berechne die Zahl x 1 = -p/2 + w Berechne die Zahl a 2 ; Nenne diese Zahl b Berechne die Zahl x 2 = -p/2 - w Berechne die Zahl b-q ; Nenne diese Zahl c Berechne die Zahl c ; Nenne diese Zahl d Berechne die Zahl -a ; Nenne diese Zahl e Berechne die Zahl e + d ; Nenne diese Zahl x 1 Berechne die Zahl e - d ; Nenne diese Zahl x 2 Anzahl Berechnungen Anzahl Zuweisungen Anzahl Variablen A 1 10 3 5 A 2 7 7 9 FHSymbol 1 Welcher Algorithmus ist besser ? Warum ?

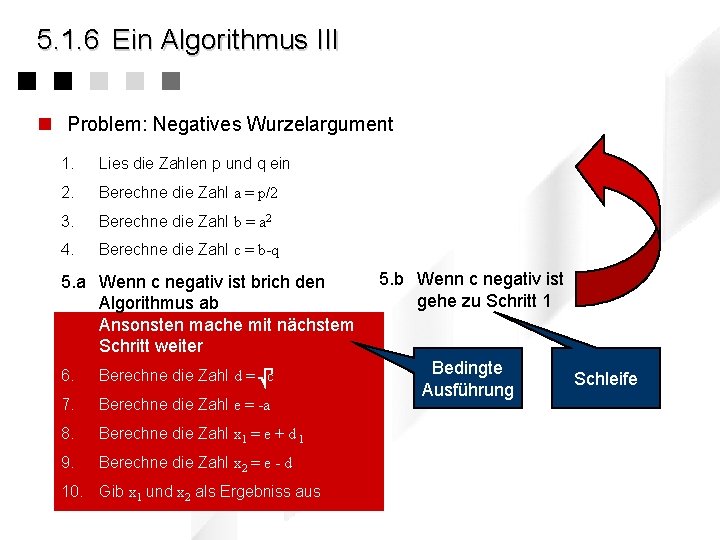
5. 1. 6 Ein Algorithmus III n Problem: Negatives Wurzelargument 1. Lies die Zahlen p und q ein 2. Berechne die Zahl a = p/2 3. Berechne die Zahl b = a 2 4. Berechne die Zahl c = b-q 5. a Wenn c negativ ist brich den Algorithmus ab Ansonsten mache mit nächstem Schritt weiter 6. Berechne die Zahl d = c 7. Berechne die Zahl e = -a 8. Berechne die Zahl x 1 = e + d 1 9. Berechne die Zahl x 2 = e - d 10. Gib x 1 und x 2 als Ergebniss aus 5. b Wenn c negativ ist gehe zu Schritt 1 Bedingte Ausführung Schleife

5. 1. 7 Fragestellungen 1. Lies die Zahlen p und q ein 2. Berechne die Zahl a = p/2 3. Berechne die Zahl b = a 2 4. Berechne die Zahl c = b-q 6. Berechne die Zahl d = c 7. Berechne die Zahl e = -a 8. Berechne die Zahl x 1 = e + d 1 9. Berechne die Zahl x 2 = e - d 10. Gib x 1 und x 2 als Ergebniss aus FHSymbol 1 Welche offenen Fragen bestehen noch ? n n n n Wer gibt p und q ein ? Wie wird p und q eingegeben ? Werden p und q in endlicher Zeit eingegeben ? Sind p und q im richtigen Format ? Ist Variable a im richtigen Format ? Gibt es die Quadrat-Funktion ? Ist c positiv ? Ist Variable e im richtigen Format ? Sind die restlichen Variablen im richtigen Format Reicht die Genauigkeit der Darstellung ? Wo wird das Ergebnis ausgegeben ? Ist ausreichend Variablenkapazität für den Algorithmus vorhanden ? Läuft der Algorithmus schnell genug ? . . .

5. 1. 8 Ein weiterer Algorithmus

5. 2 Definition n Der Begriff des Algorithmus ist zentral in der Informatik und soll in diesem Unterkapitel formal definiert werden n Inhalt 1. 2. 3. 4. 5. 6. Herkunft Der Algorithmus Beispiel: Algorithmenbeweis Weitere Prinzipien Algorithmen und Programme Ausflug: Algorithmus und Win. OSe

5. 2. 1 Herkunft n Muhammad ibn Musa abu Djafar al-Choresmi (ca. 780 -850 n. Chr) n arabischer Mathematiker, geboren in Choresmien (heute: Usbekistan) n lebte und wirkte in Bagdad im „Haus der Weisheit“ n war beteiligt an der Übersetzung der Werke griechischer Mathematiker ins Arabische n schrieb ein „Kurzgefasstes Lehrbuch für die Berechnung durch Vergleich und Reduktion“ n die lateinische Übersetzung dieses Buches („liber algorismi“) kam durch Kreuzfahrer nach Europa n verfasste auch ein Buch mit dem Titel „Al-Mukhtasar fi Hisab al-Jahr va l -Muqabala“ Algorithmus Algebra

5. 2. 2 Der Algorithmus n Definition: Ein Algorithmus (algorithm) ist die Beschreibung eines Verfahrens, um aus gewissen Eingabegrößen bestimmte Ausgabegrößen zu berechnen. Dabei müssen folgende Bedingungen erfüllt sein n Spezifikation n Durchführbarkeit n Korrektheit n Verfahren ohne Verständnis des Problemes FHSymbol 1 Erwarten Sie nie, dass ein Computer für Sie mitdenkt

5. 2. 2 Der Algorithmus : Spezifikation n Eingabespezifikation: n Es muss genau spezifiziert sein, welche Eingabegrößen erforderlich sind und welchen Anforderungen diese Größen genügen müssen, damit das Verfahren funktioniert EINGABE Algorithmus n Ausgabespezifikation n Es muss genau spezifiziert sein, welche Ausgabegrößen (Resultate) mit welchen Eigenschaften berechnet werden

5. 2. 2 Der Algorithmus : Durchführbarkeit n Endliche Beschreibung n das Verfahren muss in einem endlichen Text vollständig beschrieben sein n Effektivität n Jeder Schritt des Verfahrens muss effektiv (d. h. tatsächlich) „mechanisch“ ausführbar sein Bem. : „Effektivität“ ist nicht zu verwechseln mit „Effizienz“ („Wirtschaftlichkeit“) n Determiniertheit n Der Verfahrensablauf ist zu jedem Zeitpunkt fest vorgeschrieben

5. 2. 2 Der Algorithmus : Korrektheit n partielle Korrektheit n Jedes berechnete Ergebnis genügt der Ausgabespezifikation, sofern die Eingaben der Eingabespezifikation genügt haben n Terminierung n Der Algorithmus hält nach endlich vielen Schritten mit einem Ergebnis an, sofern die Eingaben der Eingabespezifikation genügt haben

5. 2. 2 Der Algorithmus : Zusammenfassung n Definition Ein Algorithmus (algorithm) ist die Beschreibung eines Verfahrens, um aus gewissen Eingabegrößen bestimmte Ausgabegrößen zu berechnen, der gekennzeichnet ist durch: 1. 2. 3. 4. 5. 6. 7. Spezifikation der Ein- und Ausgabegrößen eine endliche Beschreibung des Verfahrens effektive Ausführbarkeit der Verfahrensschritte Determiniertheit der Verfahrensschritte partielle Korrektheit Terminiertheit n Bemerkung: n Algorithmen, die eine oder mehrere dieser Eigenschaften nicht besitzen werden dann als Nicht-<Eigenschaft> Algorithmen bezeichnet. l Bsp: Nicht-Deterministische Algorithmen.

5. 2. 3 Beispiel: Algorithmenbeweis n In gängiger mathematischer Notation könnte ein Verfahren zur Berechnung der Modulus-Funktion a mod b wie folgt aussehen: a falls a < b mod(a, b) = mod(a-b, b) falls a b n Um festzustellen, ob diese Berechnungsvorschrift einen Algorithmus im Sinne der Definition darstellt, müssen folgende Punkte beachten werden: n Spezifikation l Eingabe l Ausgabe n Durchführbarkeit l Endliche Beschreibung l Effektivität l Determiniertheit n Korrektheit l Partielle Korrektheit l Terminierung

5. 2. 3 Beispiel: Spezifikation n Lassen sich die möglichen Ein- und Ausgabewerte genau spezifizieren ?

5. 2. 3 Beispiel: Durchführbarkeit n Ist der Algorithmus durchführbar ?

5. 2. 3 Beispiel: Korrektheit (partielle) n Ist der Algorithmus korrekt (im Sinne der Spezifikation)

5. 2. 3 Beispiel: Korrektheit (Terminierung) n Terminiert der Algorithmus ? n Bemerkung: Es gibt kein Verfahren, das zu einem beliebigen Algorithmus angibt, ob er terminiert oder nicht („Halte-Problem“)

5. 2. 3 Weitere Prinzipien n Neben den in der Definition angegebenen Eigenschaften gibt es weitere wichtige Prinzipien, die bei der Erstellung eines Algorithmuses zu beachten sind: n Effizienz l Der Algorithmus soll möglichst wenig Aufwand verursachen – Das Ergebnis mit möglichst wenig Rechenschritten (oder mit möglichst wenig Speicherbedarf) erzielen n Korrektheit beweisbar? l Ein nicht-korrekter Algorithmus ist nach unserer Definition kein Algorithmus! l Trotzdem sind nicht-korrekte Verfahren eher die Regel als die Ausnahme

5. 2. 4 Algorithmen und Programme: Der Weg Problem Algorithmierung Spezifizieren Algorithmus Programmierung Verifizieren Programm Testen n gegeben: das Problem n durch Spezifizieren wird das Problem formal beschrieben n Durch Algorithmierung (Algorithmenentwurf) wird ein Algorithmus erzeugt n durch Verifizieren kann der Algorithmus auf Übereinstimmung mit der Spezifikation überprüft werden n Durch Programmieren wird aus den Algorithmus ein Programm erzeugt n durch Testen kann das Programm auf Übereinstimmung mit der Spezifikation und dem Algorithmus überprüft werden.

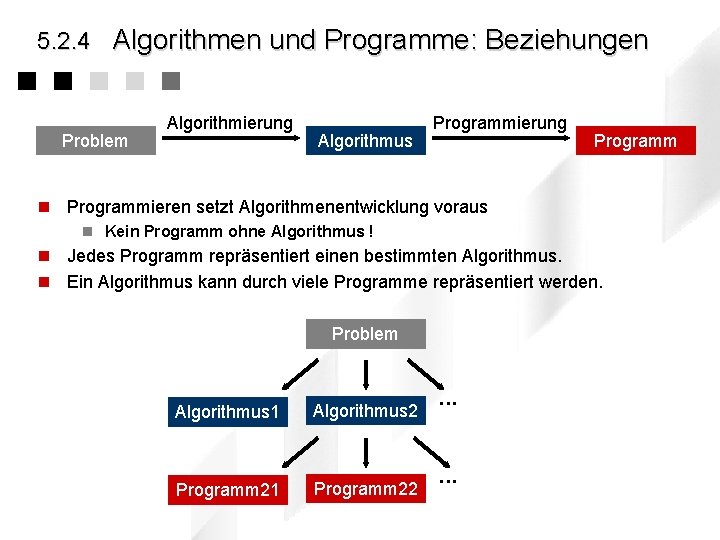
5. 2. 4 Algorithmen und Programme: Beziehungen Problem Algorithmierung Algorithmus Programmierung Programm n Programmieren setzt Algorithmenentwicklung voraus n Kein Programm ohne Algorithmus ! n Jedes Programm repräsentiert einen bestimmten Algorithmus. n Ein Algorithmus kann durch viele Programme repräsentiert werden. Problem Algorithmus 1 Algorithmus 2 Programm 21 Programm 22 . . .

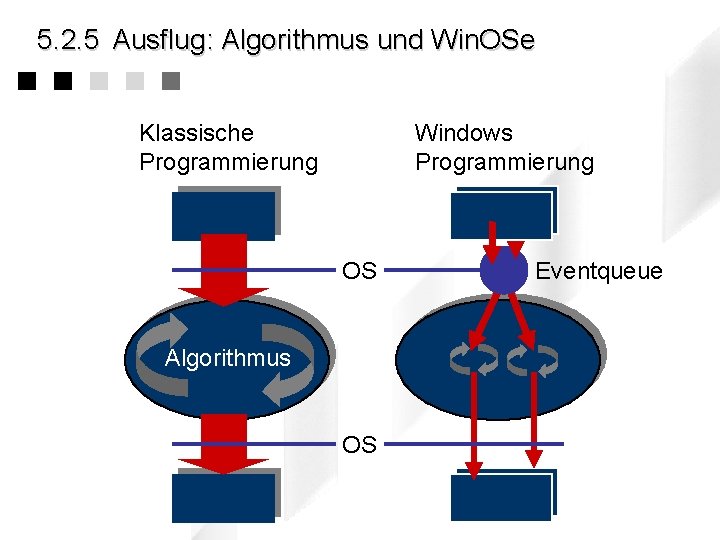
5. 2. 5 Ausflug: Algorithmus und Win. OSe Klassische Programmierung Windows Programmierung OS Algorithmus OS Eventqueue

5. 3 Strukturelemente n Um die Dynamik - also die Abfolge von Aktionen - eines Algorithmuses zu beschreiben, benötigt man formale Beschreibungsmittel, sowie eine Festlegung, wie diese Beschreibungmittel zu notieren und zu interpretieren sind. Dieses Unterkapitel stellt die formalen Beschreibungsmittel für Algorithmen vor. Diese Beschreibungsmittel sind dabei gleichzeitig Strukturierungselemente für Algorithmen, denn sie definieren die Struktur von Algorithmen. n Inhalt: 1. 2. 3. 4. Die Elemente Folge Auswahl Wiederholung

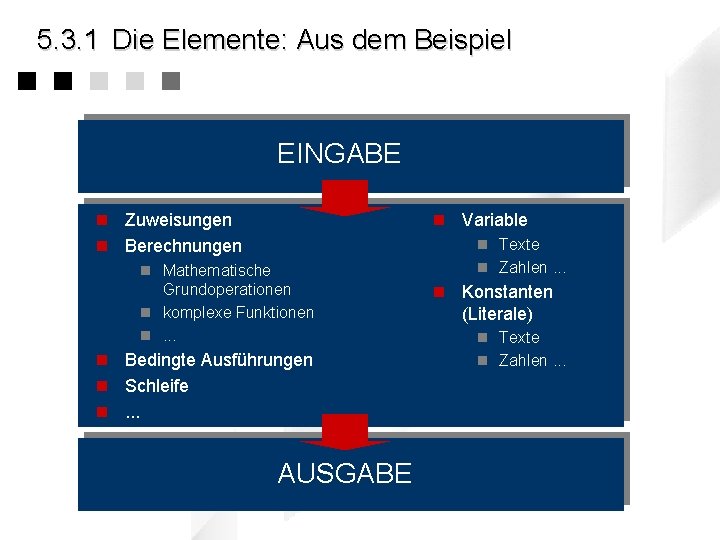
5. 3. 1 Die Elemente: Aus dem Beispiel EINGABE n Zuweisungen n Berechnungen n Variable n Mathematische Grundoperationen n komplexe Funktionen n. . . n Bedingte Ausführungen n Schleife n. . . AUSGABE n Texte n Zahlen. . . n Konstanten (Literale) n Texte n Zahlen. . .

5. 3. 1 Die Elemente: Notation n Für die Beschreibung von Algorithmen gibt es viele Möglichkeiten n Alltagssprache n Konkrete Programmiersprache n Dazwischen gibt es eine Vielzahl von Notationen, die den Übergang zwischen Problembeschreibung und Programm erleichtern sollen n Eine mögliche - eindimensionale - Notation ist Pseudocode: n // Dies ist eine Zuweisung x = 42; l Kommentare werden (hier) mit vorangestellten Slashes „//“ gekennzeichnet l Aktionen werden (hier) mit Semikolon „; “ getrennt n Visualisierung durch graphische - zweidimensionale -Notation n Flussdiagramme n Struktogramme (=Nasi-Schneidermann-Diagramme) Aktion

5. 3. 1 Die Elemente: atomaren Elemente n Anweisungen sind die atomaren Elemente eines Algorithmus‘, die Elemente also, aus denen ein Algorithmus aufgebaut ist. n Es gibt (zunächst) drei Arten dieser „atomaren“ Elemente n Zuweisung: l Pseudocode X = y; l Auf der linken Seite der Zuweisung steht eine Variable auf der rechten Seite der Zuweisung steht entweder eine Variable, ein Literal oder eine Berechnung aus Varaibelen und Literalen n Eingabe l Pseudocode: x << <Eingabegerät> ; l Als Eingabegerät kann ein geeignetes physikalisches Geraöt (Tastatur, Schnittstelle, . . . ) angegeben werden. n Ausgabe l Pseudocode: x >> <Ausgabegerät> ; l Als Ausgabegerät kann ein geeignetes physikalisches Geraöt (Bildschirm, Drucker, Schnittstelle, . . . ) angegeben werden n Ein- und Ausgabe können auch als Zuweisung verstanden werden.

5. 3. 1 Die Elemente: Kontrollelemente n Die atomaren Elemente eines Algorithmuses können durch drei einfache Strukturierungsmethoden, den „Kontrollelementen“, zueinander in Beziehung gesetzt werden: 1. Folge (Sequenz) 2. Auswahl (Selektion, Fallunterscheidung) 3. Wiederholung (Iteration, Schleife) n Die Kontrollelemente bestimmen die Reihenfolge von Aktionen in Algorithmen n Eine Aktion (Ai) - auch Verarbeitung genannt - ist ein atomares Element oder eine durch die Strukturmethoden zusammengefasste Menge mehrerer Aktionen

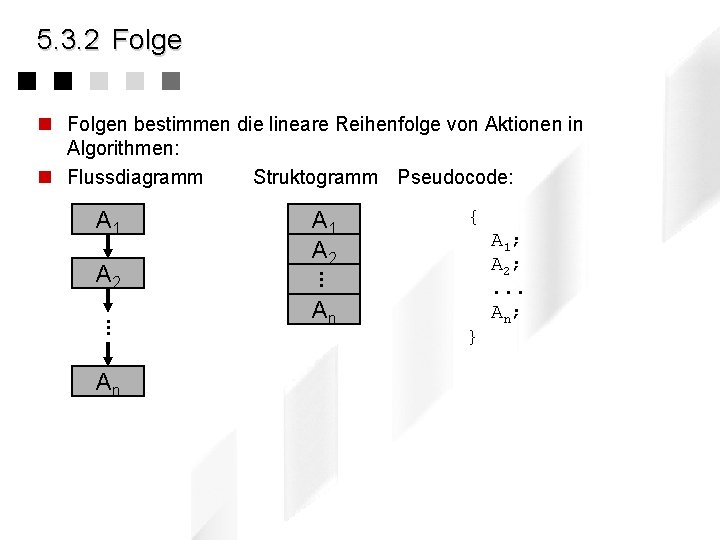
5. 3. 2 Folge n Folgen bestimmen die lineare Reihenfolge von Aktionen in Algorithmen: n Flussdiagramm Struktogramm Pseudocode: A 1 A 2. . . An A 1 A 2 { . . . An } A 1; A 2; . . . An;

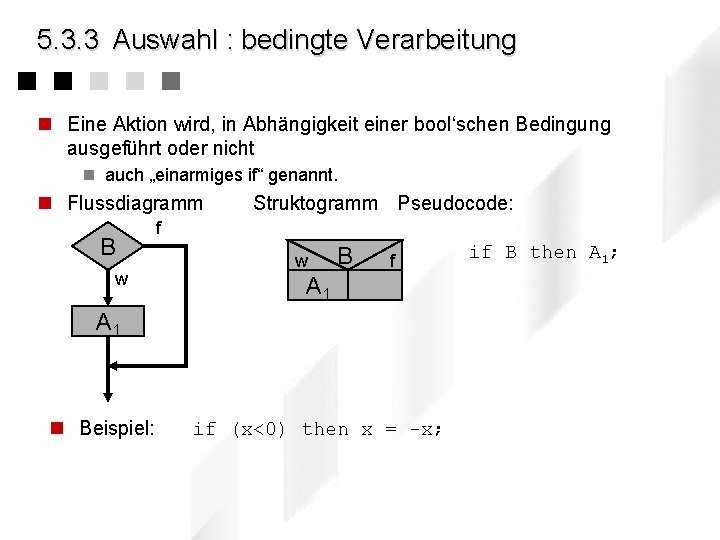
5. 3. 3 Auswahl : bedingte Verarbeitung n Eine Aktion wird, in Abhängigkeit einer bool‘schen Bedingung ausgeführt oder nicht n auch „einarmiges if“ genannt. n Flussdiagramm B w Struktogramm Pseudocode: f w B f A 1 n Beispiel: if (x<0) then x = -x; if B then A 1;

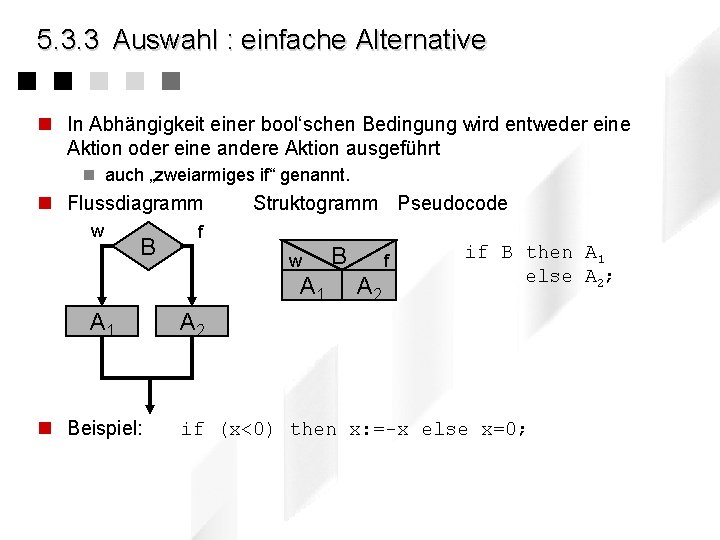
5. 3. 3 Auswahl : einfache Alternative n In Abhängigkeit einer bool‘schen Bedingung wird entweder eine Aktion oder eine andere Aktion ausgeführt n auch „zweiarmiges if“ genannt. n Flussdiagramm w B Struktogramm Pseudocode f w A 1 n Beispiel: B f A 2 if B then A 1 else A 2; A 2 if (x<0) then x: =-x else x=0;

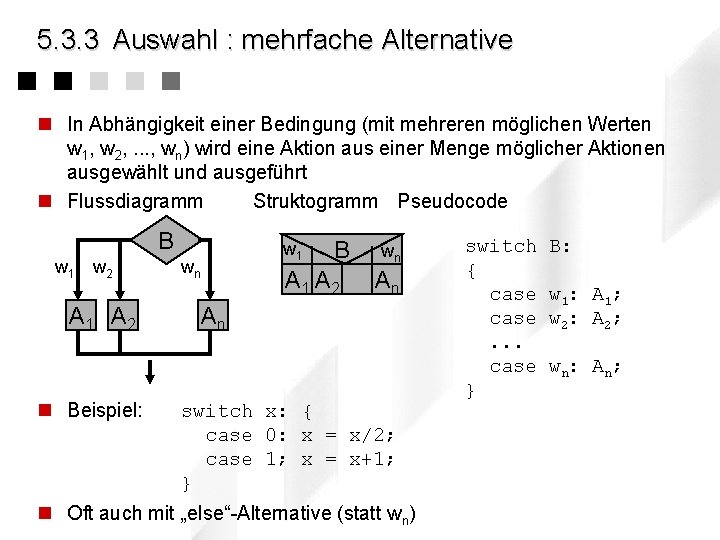
5. 3. 3 Auswahl : mehrfache Alternative n In Abhängigkeit einer Bedingung (mit mehreren möglichen Werten w 1, w 2, . . . , wn) wird eine Aktion aus einer Menge möglicher Aktionen ausgewählt und ausgeführt n Flussdiagramm Struktogramm Pseudocode B w 1 w 2 A 1 A 2 n Beispiel: wn w 1 B A 1 A 2 wn An An switch x: { case 0: x = x/2; case 1; x = x+1; } n Oft auch mit „else“-Alternative (statt wn) switch { case. . . case } B: w 1: A 1; w 2: A 2; wn: An;

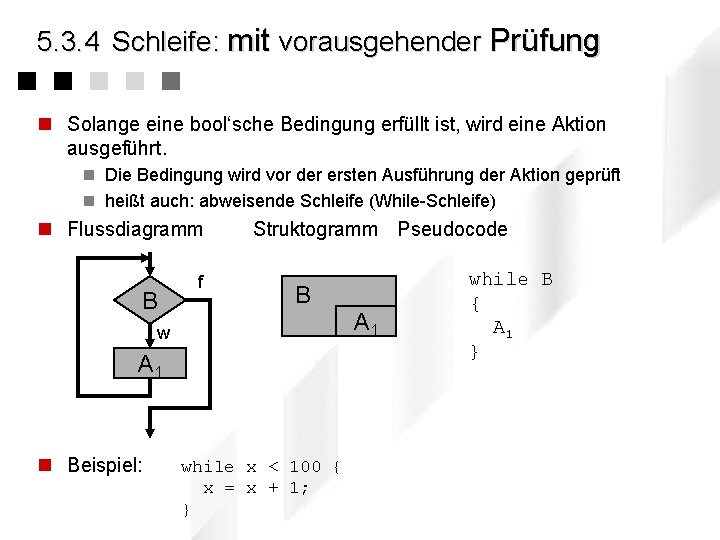
5. 3. 4 Schleife: mit vorausgehender Prüfung n Solange eine bool‘sche Bedingung erfüllt ist, wird eine Aktion ausgeführt. n Die Bedingung wird vor der ersten Ausführung der Aktion geprüft n heißt auch: abweisende Schleife (While-Schleife) n Flussdiagramm B f Struktogramm Pseudocode B A 1 w A 1 n Beispiel: while x < 100 { x = x + 1; } while B { A 1 }

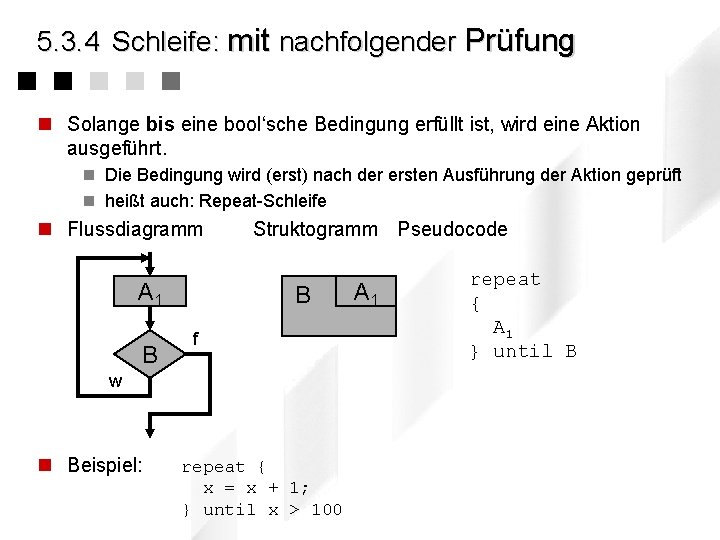
5. 3. 4 Schleife: mit nachfolgender Prüfung n Solange bis eine bool‘sche Bedingung erfüllt ist, wird eine Aktion ausgeführt. n Die Bedingung wird (erst) nach der ersten Ausführung der Aktion geprüft n heißt auch: Repeat-Schleife n Flussdiagramm A 1 B Struktogramm Pseudocode B f w n Beispiel: repeat { x = x + 1; } until x > 100 A 1 repeat { A 1 } until B

5. 3. 4 Schleife: Beispiel (abweisende Schleife) n Untersuche ob eine gegebene natürliche Zahl Primzahl ist. n p > 2 ist Primzahl, falls sie durch kein t mit 1<t<p teilbar ist (p mod t 0) n Idee: n wenn p Primzahl, dann ist p ungerade n es genügt, nur ungerade t zu untersuchen n es genügt, nur solche t zu untersuchen die kleiner p sind, n Algorithmus: p << Tastatur; if ((p>2) and (p mod 2 != 0)) then { t = 3; // initialize t while ((t*t<p) and (p mod t != 0)) { t = t + 2; } // nach Schleife ist t*t >=p oder p mod t == 0 if (t*t>p) then „p ist Primzahl“ >> Bildschirm; else „p ist keine Primzahö“ >> Bildschrim; } else { „p <= 2 oder p gerade“ >> Bildschirm; } // Primzahl ?

5. 3. 4 Schleife: Beispiel (Vergleich while repeat) n Sind diese Schleifen im Ergebnis identisch ? while x < 100 repeat { { x = x + 1; } } until x > 100 n und jetzt ? repeat { x = x + 1; } until x >= 100 n Letzer Versuch: if (x <= 100) then { repeat { x = x + 1; } until x >= 100 } n Welche Lösung ist eleganter ? n aber: oft wird eine erstmalige Aktion benötigt, um ein Datum überhaupt überprüfen zu können.

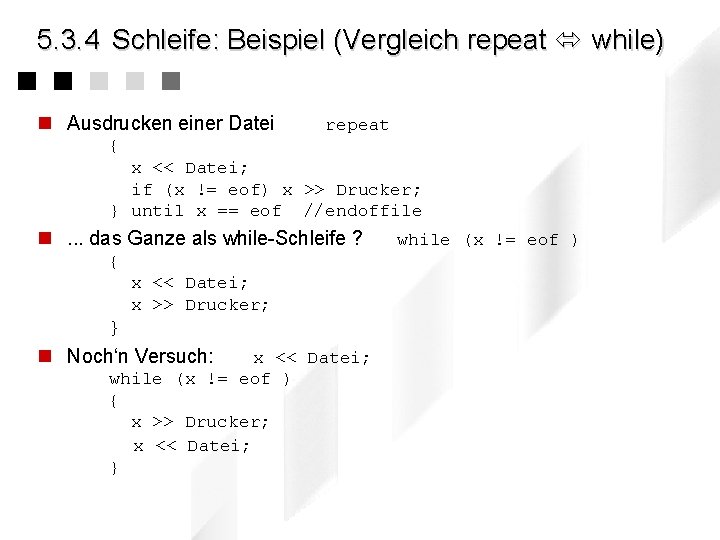
5. 3. 4 Schleife: Beispiel (Vergleich repeat while) n Ausdrucken einer Datei repeat { x << Datei; if (x != eof) x >> Drucker; } until x == eof //endoffile n. . . das Ganze als while-Schleife ? { x << Datei; x >> Drucker; } n Noch‘n Versuch: x << Datei; while (x != eof ) { x >> Drucker; x << Datei; } while (x != eof )

5. 3. 4 Schleife: Beispiel (Schleife mit Zählern) n Sehr häufig werden Schleifen verwendet, deren Bedingung abhängig von Zählerwerten sind. n Die Zählerwerte werden vor Eintritt in die Schleife initialisiert n Die Bedingung prüft den Zählerwert n Im Schleifenkörper wird der Zähler erhöht (increase) oder erniedrigt (decrease) l Vorsicht mit: dem Zählertyp, dem Additionswert, der Bedingung n Algorithmus: // --- Initialisierung ---------------s = 0; i = 1; // Initialisierung des Schleifenzählers // --- Schleife (Berechnet Summe 1. . n) ------while ( i <= n ) { s = s + i; i = i + 1; // Erhöhung des Schleifenzählers (oft um 1) }

5. 2. 4 Schleife: Die „For“-Schleife n Da Schleifen mit Zähler sehr häufig auftreten, stellen viele Programmiersprachen eigenes sprachliches Mittel dafür zur Verfügung: Die „For“ Schleife n Pseudocode: Beispiel: for var=start_value to end_value for i=1 to 10 { { A; x = x + i; } } n Der Zähler (var) wird pro Schleifendurchlauf implizit um 1 erhöht (Bei manchen Sprachen - z. B. Basic, C, C++ - kann man dies ändern) n Dieser Code ist äquivalent mit folgender Schleife: i = start_value while i <= end_value { A; i = i+1; }

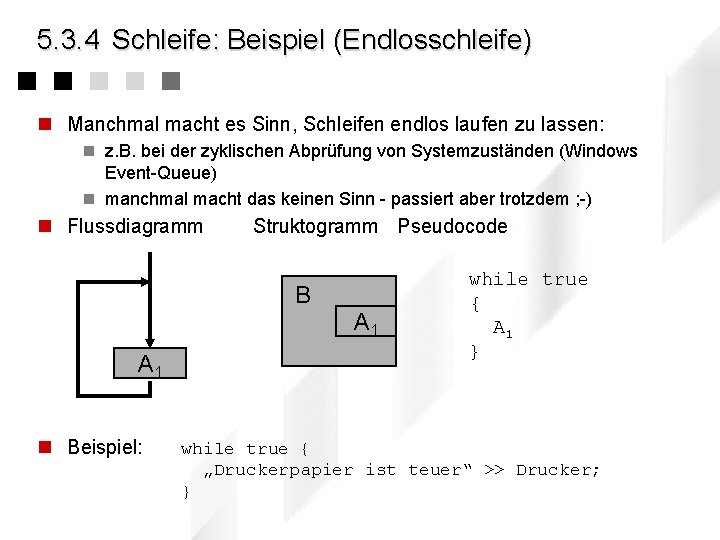
5. 3. 4 Schleife: Beispiel (Endlosschleife) n Manchmal macht es Sinn, Schleifen endlos laufen zu lassen: n z. B. bei der zyklischen Abprüfung von Systemzuständen (Windows Event-Queue) n manchmal macht das keinen Sinn - passiert aber trotzdem ; -) n Flussdiagramm Struktogramm Pseudocode B A 1 n Beispiel: while true { A 1 } while true { „Druckerpapier ist teuer“ >> Drucker; }

5. 4 Strukturierung n Mit Hilfe atomarer Elemente und der Kontrollelemente lassen sich Algorithmen strukturieren. In diesem Kapitel sind einige Begriffe zur Strukturierung erläutert. Insbesondere wird ein weiteres - viertes Kontrollelement vorgestellt (und auch gleich wieder verworfen) n Inhalt 1. 2. 3. 4. Control Flow Strukturierung durch Sprung Strukturiert-iterative Beschreibungsform Strukturierungstypen

5. 4. 1 Control Flow n Mithilfe der Kontrollelemente können die „atomaren“ Elemente (Anweisungen) strukturiert werden n Die Anordnung der Anweisungen (als atomare Elemente) eines Algorithmus, die bestimmt, in welcher Reihenfolge Dinge geschehen, heißt n control flow (Steuerungsverlauf, Kontrollfluss) des Algorithmus genannt n Manchmal wird auch der Programmablauf oder Kontrollfaden (thread of control, thread), also die tatsächlich abgespulten Schritte und Anweisungen so bezeichnet

5. 4. 2 Strukturierung durch Sprung n Bei der Vorstellung der Kontrollelemente wurde (aus hinterhältig, didaktischen) Gründen auf ein viertes Element verzichtet: Der Sprung („Goto“-Anweisung) n Die Konstruktion „fahre fort mit Schritt x“ (goto x) stellt einen solchen Sprung (jump) im Steuerungsverlauf dar n Zur Anwendung von goto werden Schritte mit einer Marke (Label) versehen, um das Ziel des Sprunges zu kennzeichnen n Dies ist die elementarste Form, eine Wiederholung oder sonstige Verzweigung im Ablauf auszudrücken n Dadurch erhalten wir die elementar-iterative Beschreibungsform von Algorithmen, die Strukturierung mit ein-/mehrfacher Auswahl und Schleifen funktional abdeckt. n Beispiel: while x<100 { 1: if x>0 100 goto 2 x = x+1; } goto 1; 2: . . .

5. 4. 2 Strukturierung durch Sprung n Anwendung von Sprüngen ist sehr gefährlich! n Sprünge strukturieren komplexe Programm nicht ausreichend - der Steuerungsverlauf kann verworren und unübersichtlich sein n Um den Steuerungsverlauf auch bei komplexen Algorithmen übersichtlich zu halten, schränkt man die Sprünge ein: n Schleifen der Flussdiagramme sind höchstens ineinander geschachtelt n Schleifen überkreuzen sich nicht! n Bei gut strukturierten Algorithmen würde man z. B. nur wieder eine geschlossene Schleife oder einen (vorzeitigen) Sprung bedingt durch die Behandlung des. Trivialfalls erlauben n Wir sprechen in diesem Fall von strukturierten Sprüngen im Gegensatz zu freien Sprüngen, die prinzipiell beliebige Ziele haben können

5. 4. 3 Strukturiert-iterative Beschreibungsform n Sprünge können die bestimmte „höhere“ Strukturierungsarten funktional abzubilden. Hier gilt auch der Umkehrschluss n In der strukturiert-iterativen Beschreibungsform kommen Sprünge nur noch implizit bei der Ausführung höherer Iterationsstrukturen vor n Dieses sind Fallunterscheidungen (Auswahl) wie if-then-else n oder insbesondere Schleifenkonstrukte n Diese bewirken, dass der Programmfluss n In einer Auswahl zu genau einer Auswahl geht. n in einer Schleife von einer Prüfung zu den Aktionen des Schleifenkörpers und wieder zurück zur Prüfung geht. n Viele höhere Programmiersprachen (Pascal, C, C++) erlauben jedoch die Verwendung von Sprüngen n Aus Optimierungsgründen (Nähe zur Maschinensprache) n Aus Strukturierungsgründen)

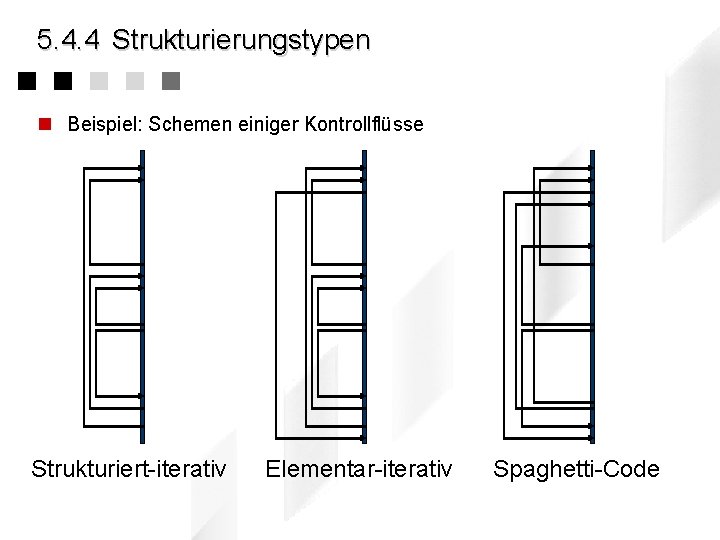
5. 4. 4 Strukturierungstypen n Beispiel: Schemen einiger Kontrollflüsse Strukturiert-iterativ Elementar-iterativ Spaghetti-Code

5. 5 Blockung n Mit Hilfe der bislang vorgestellten Kontrollelemente lassen sich die atomaren Elemente (Anweisungen) eines Algorithmus‘ zu einem Kontrolfluss strukturieren. Wie wir gesehen haben, kann dieser Kontrollfluss mehr oder weniger „wohlstrukturiert“ sein. In diesem Unterkapitel wird eine Element beschrieben, mit dem Aktionen statisch nochmals zusammengefasst werden können. Diese Zusammenfassung hat auch Einfluss auf das dynamische Verhalten von Verarbeitungsobjekten (Variable). n Inhalt: 1. 2. 3. 4. 5. 6. 7. 8. Die Idee Notation Formale Parameter Beispiel: Ein einfacher Block Eigenschaften Beispiel: Seiteneffekte Vorzeitiges Verlassen Goldene Regeln

5. 5. 1 Die Idee n Idee: Eine Zusammenfassung von Aktionen bekommt einen Namen und kann durch das Nennen des Namens (Aufruf) aktiviert werden. n In einen Block sollen Daten formal hinein und herausgelangen n Ein Block soll eigenen Daten besitzen n Vorteile: n Gliederung des Algorithmus‘ durch hierarchische Dekomposition („Divide et impera: Teile und herrsche“) n Wiederverwendbarkeit durch mehrfachen Aufruf statt durch mehrfaches notieren. l universeller ( Anzahl muss nicht bekannt sein) l fehlerunanfälliger n Kapselung unwichtiger Details („information Hiding“) n Vorteile bei der Organisation von Programmiertätigkeit durch Verteilbarkeit der Aufgaben.

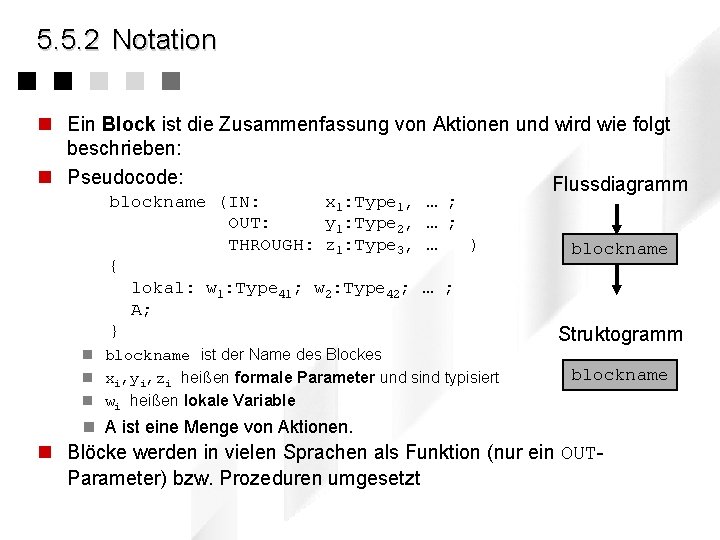
5. 5. 2 Notation n Ein Block ist die Zusammenfassung von Aktionen und wird wie folgt beschrieben: n Pseudocode: Flussdiagramm blockname (IN: x 1: Type 1, OUT: y 1: Type 2, THROUGH: z 1: Type 3, { lokal: w 1: Type 41; w 2: Type 42; A; } … ; … ) blockname … ; n blockname ist der Name des Blockes n xi, yi, zi heißen formale Parameter und sind typisiert n wi heißen lokale Variable Struktogramm blockname n A ist eine Menge von Aktionen. n Blöcke werden in vielen Sprachen als Funktion (nur ein OUTParameter) bzw. Prozeduren umgesetzt

5. 5. 3 Formale Parameter n IN-Parameter (Eingabeparameter) sind Parameter, die an den Block übergeben werden n Dazu werden beim Aufruf des Blockes an die Stelle der Eingabeparameter Variable, Literale oder Ausdrücke (Berechnungen) notiert. Diese werden beim Aufruf zu Werten transformiert, die an den entsprechnden Variablen zugewisen werden. (call by value) n OUT-Parameter (Ausgabeparameter) sind Parameter, die aus dem Block durch Zuweisung an Variable zurückgegeben werden. n Dazu werden beim Aufruf des Blockes an die Stelle der Ausgabeparameter Variablen notiert, die nach dem Aufruf die zurückgegeben Werte beinhalten (call-by refernce) n THROUGH-Parameter (Ein-/Ausgabeparameter) sind Parameter die Werte in den Block hinein und hinaus übermitteln. n Eingabe wie bei IN-Parametern (aber: nur Angabe einer Variable) n Rückgabe wie bei OUT-Parametern

5. 5. 4 Beispiel: Ein einfacher Block n Ein Block zur Berechnung von Summen (mit Aufrufzähler) summe (IN: value 1 : Integer; value 2 : Integer; OUT: result : Integer; THROUGH: counter : Integer ) { i : integer: // lokale Variable result = 0; // Initialisierung for i=1 to value 2 // ein wenig umständlich result = value 1 + 1; counter = counter + 1; } n Aufruf anzahl = 1; // schon erste Summe hat zwei Summanden initial = 5; summe(initial, 9, ergebnis, anzahl); summe(ergebnis, 9, ergebnis, anzahl); ergebnis/anzahl >> Bildschirm // Mittelwert

5. 5. 5 Eigenschaften n Jeder Block kann über einen Satz lokaler Variable verfügen, die außerhalb des Blockes nicht sichtbar sind n Die Variablenbezeichner können also außerhalb ohne Einfluss auf den Block verwendet werden n Auch die in der Blockdefinition als formale Parameter verwendeten Variablenbezeichner sind nur im Block sichtbar: l Auch sie können außerhalb ohne Einfluss verwendet werden, l Aber Vorsicht: die Veränderung von IN und THROUGH-Parametern bewirkt (oft) eine Veränderung der beim Aufruf verwendeten zugehörigen Parameter (der zugehörigen „gebundenen“ Parameter). n Variable, die in einem Block verwendet aber nicht deklariert werden, werden als „global“ angenommen n Viele Sprachen erlauben die Definition von Blöcken innerhalb von Blöcken n Variablen, die in einem Block nicht deklariert sind, werden im umgebenden Block vermutet.

5. 5. 6 Beispiel: Seiteneffekt n Das (ungewollte) implizite Verändern von „äußeren“ Parametern durch Veränderung „innerer“ Parameter nennt man „Seiteneffekt“ summe (THROUGH: value 1 : Integer; value 2 : Integer; result : Integer; ) { value 1 = value 1 + value 2; result = value 1; } n Aufruf x = 5; y = 7; summe (x, y, z); „Die Summe von „ >> Bildschirm; x >> Bildschirm; „und“ >> Bildschirm; y >> Bildschirm; „ ist „ >> Bildschirm; z >> Bildschirm; Die Summe von 12 und 7 Ist 12

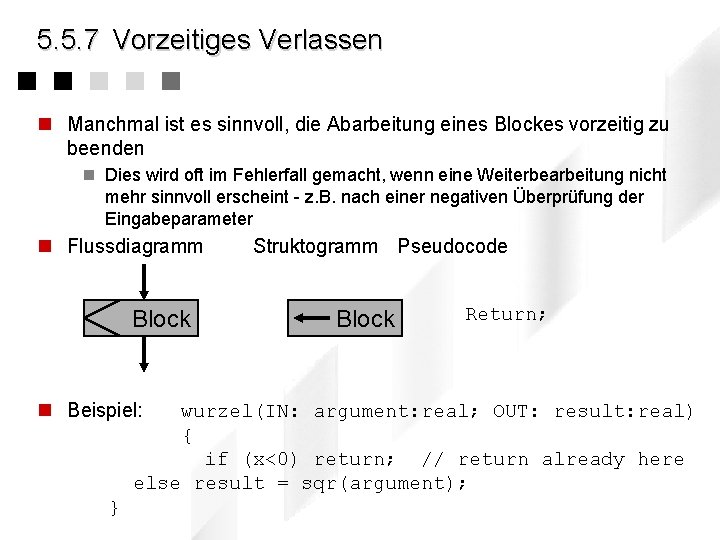
5. 5. 7 Vorzeitiges Verlassen n Manchmal ist es sinnvoll, die Abarbeitung eines Blockes vorzeitig zu beenden n Dies wird oft im Fehlerfall gemacht, wenn eine Weiterbearbeitung nicht mehr sinnvoll erscheint - z. B. nach einer negativen Überprüfung der Eingabeparameter n Flussdiagramm Block n Beispiel: Struktogramm Pseudocode Block Return; wurzel(IN: argument: real; OUT: result: real) { if (x<0) return; // return already here else result = sqr(argument); }

5. 5. 8 Goldene Regeln n Namen so lokal wie möglich deklarieren n Möglichst keine globalen Variablen verwenden n Wenn doch: l Ganz wenige - nur eine (z. B. strukturiert) l Auffällig kennzeichnen: z. B. global_error_handle n Nach Möglichkeit „call by value“ verwenden n Wird nicht von allen Programmiersprachen unterstützt n Probleme bei der Rückgabe umfangreicher Daten (wg. Umkopieren) n Blöcke sind so zu wählen dass: n Der innere Zusammenhang stark ist n Der äußere Zusammenhang schwach ist (minimale Schnittstellen, keine Datenteilung , z. B. durch globale Variable)

5. 6 Iteration und Rekursion n Im Bereich der Datenstrukturen haben wir es oft mit rekursiven Strukturen z. B. Bäumen zu tun. Auch in der Mathematik sind rekursive Definition weit verbreitet. und finden über zugehörige Algorithmen Einzug in die Informatik. Das Konzept der Rekursion wird in der Informatik allerdings teilweise mit Skepsis umgesetzt, führt es doch, in ungeeigneten Fällen, zu inakzeptablen Laufzeiten. Hinzu kommt, dass einige Programmierspachen (z. B. FORTRAN) Rekursion nicht unterstützen. In diesem Unterkapitel soll auf die Möglichkeiten der Verwendung von Rekursion bzw. Iteration eingegangen werden n Inhalt 1. 2. 3. 4. 5. Definition Beispiele Aufrufverwaltung Wo nicht und wo

5. 6. 1 Definition: Rekursion n Ein Objekt heißt rekursiv, wenn es sich selbst als Teil enthält oder mit Hilfe von sich selbst definiert ist. n Wesentlich ist die Möglichkeit, unendliche Mengen von Objekten durch eine endliche Aussage zu definieren. n Bsp. : Definition natürlicher Zahlen: l 0 sei eine natürliche Zahl l Der Nachfolger (n+1) einer natürlichen Zahl ist wieder eine natürliche Zahl n Ein Algorithmus heißt rekursiv, wenn er sich selbst als einen seiner Aktionen (Verarbeitungsschritten) enthält. n In der Regel enthält er sich mit „verkleinerter“ Aufgabenstellung. n Damit er terminiert, muss er einen Zweig beinhalten, der einen (den) elementaren Wert nicht rekursiv bestimmt. (den Basisfall) n Objekte (Algorithmen), die andere Objekte (Algorithmen) enthalten, die wiederum die ursprünglichen Objekte (Algorithmen) enthalten, heißen indirekt rekursiv

5. 6. 2 Beispiel: Hilbert-Kurven n D. Hilbert: Über stetige Abbildungen einer Linie auf ein Flächenstück, Math. Annalen, 1891: Hilbert (IN: s, t, v : integer) { // s: Größe, t: Rekursionstiefe, v: +-1 Orientierung if (t>0) then { turnleft(v*90); // 90 Grad links t=1 hilbert(s/2, t-1, -v); // rekursiver Aufruf forward(s); // zeichne Strecke s turnright(v*90); // 90 Grad rechts hilbert(s/2, t-1, v); // rekursiver Aufruf forward(s); // zeichne Strecke s t=2 hilbert(s/2, t-1, v); // rekursiver Aufruf turnright(v*90); // 90 Grad rechts forward(s); // zeichne Strecke s hilbert(s/2, t-1, -v); // rekursiver Aufruf turnleft(v*90); // 90 Grad links } }

5. 6. 2 Beispiel: Fakultät n Mathematisch rekursive Definition: n! 1 n=0 = n x (n - 1) ! n>0 n Algorithmisch rekursive Definition: fakultaet (IN: n: integer, OUT: result: integer) { if (n == 0) then result = 1; else { fakultaet (n-1, ergebnis); ergebnis = ergebnis x n; } }

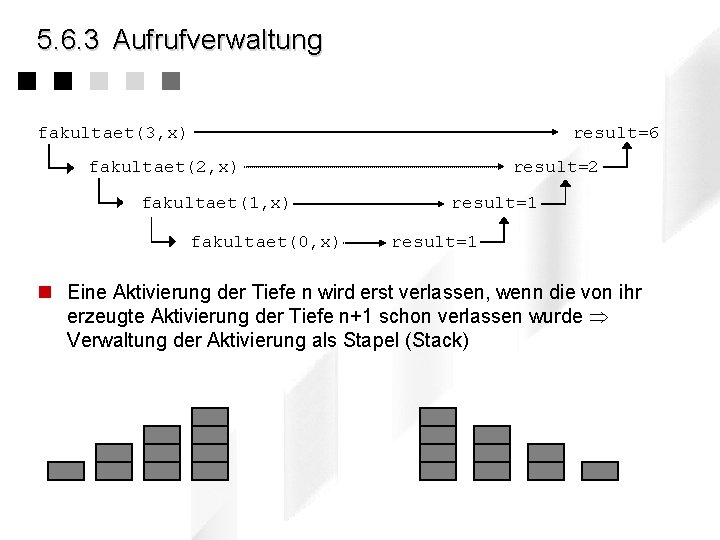
5. 6. 3 Aufrufverwaltung fakultaet(3, x) result=6 fakultaet(2, x) fakultaet(1, x) fakultaet(0, x) result=2 result=1 n Eine Aktivierung der Tiefe n wird erst verlassen, wenn die von ihr erzeugte Aktivierung der Tiefe n+1 schon verlassen wurde Verwaltung der Aktivierung als Stapel (Stack)

5. 6. 4 Wo nicht: Modulo-Berechnung n Alle Grundrechenarten - und vergleichbar einfache mathematische Operationen - lassen sich mit Hilfe sog. „Primitiv Rekursiver Funktionen“ beschreiben (siehe Beispiel. „Algorithmenbeweis“) a falls a < b mod(a, b) = mod(a-b, b) falls a b n In gängiger mathematischer Notation könnte ein Verfahren zur Berechnung der Modulus-Funktion a mod b wie folgt aussehen: modulo (IN a, b: integer, OUT result: integer) { if (a<b) result = a; else modulo (a-b, b, result); } n Offenbar einfacher ist: result = a - (a/b) x b

5. 6. 4 Wo nicht: Fibonacci-Zahlen n Fibonacci definiert im 13. Jahrhundert eine Zahlenfolge mit der die Verhältnisse des „goldenen Schnitts“ ebenso beschrieben werden können, wie die Populationsentwicklung in einem Kaninchenstall: 0 n=0 fib(n) = 1 n=1 fib(n-2)+fib(n-1) n>1 n fib(IN: n: integer, OUT: result: integer) { r, s : integer; if (n==0) then result = 0 else if (n==1) then result = 1 else { fib(n-1, r); fib(n-2, s); result = r + s; } } 0 1 1 2 3 5 8 13 21 34 55 89 144 233. . .

5. 6. 4 Wo nicht: Fibonacci-Zahlen 0 n fib(IN: n: integer, OUT: result: integer) {. . . fib(n-1, r); fib(n-2, s); result = r + s; . . . } 1 n n Aufrufe Rechenzeit (1 Aufruf = 1 nsec) 1 0 1 n Zeit 2 1 1 10 0, 18 sec 3 20 22 sec 5 3 5 50 41 sec 8 4 9 100 36000 Jahre 5 15 13 6 25 21 n Die Anzahl der Aufrufe verhält sich offenbar selbst ähnlich 34 der Fibonacci-Reihe: n Anzahl (n) = 2 x fib(n+1) - 1 n Anstieg ist praktisch exponentiell also nicht verwendbar 55 89 144 233. . .

5. 6. 4 Wo nicht: Fibonacci-Zahlen 0 1 1 2 3 5 8 fib 13 21 34 55 89 144 233. . . n Idee: Merken von zwei Folgewerten in Variablen und Aufsummieren in Schleife, wobei die Werte immer umgespeichert werden: fib (IN: n: integer, OUT: result: integer) { a, b, z : integer; a = 0; b = 1; // fib 0, fib 1 while (n > 0) do { z = a + b; // Berechnung der nächsten a = b; b = z; // Umspeichern der fibs n = n - 1; // dicrease n } result = a; // das Resultat steht in a } n Anzahl (n) = n n Zeit (n=100) = 1 sec (anstatt 36000 Jahre !)

5. 6. 5 Wo nicht und wo? n Man sollte überall dort auf Rekursion verzichten, wo es eine offensichtliche Lösung mit Iteration gibt. n Jeder rekursive Algorithmus lässt sich in eine iterative Form umwandeln (z. B. über explizites Ausformulieren einer Stackverwaltung) n Es gibt allerdings einige Fälle, in denen Rekursion angewandt werden sollte: n Rekursion ist überall dort sinnvoll anwendbar, wo sich ein Problem in mehrere (oft: zwei) nicht überlappende Teilprobleme aufspalten lässt und sich die Teilprobleme leicht rekombinieren lassen. n Rekursion sollte dort verwendet werden, wo die zugrunde liegenden Datenstrukturen selbst rekursiver Art sind (z. B. : Bäume) n Für einige Probleme gibt es keine direkte Vorschrift zur Berechnung. Diese können oft nur durch „Trial and Error“ gelöst werden. Oft lassen sich diese Versuche (Trials) durch Untersuchung eines Teilproblems natürlich in rekursiver Form darstellen. Dieses Vorgehen nennt man „Backtracking“

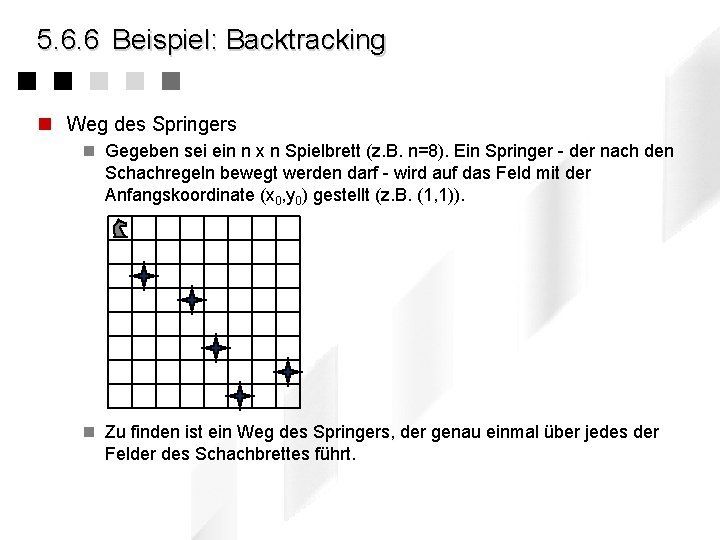
5. 6. 6 Beispiel: Backtracking n Weg des Springers n Gegeben sei ein n x n Spielbrett (z. B. n=8). Ein Springer - der nach den Schachregeln bewegt werden darf - wird auf das Feld mit der Anfangskoordinate (x 0, y 0) gestellt (z. B. (1, 1)). n Zu finden ist ein Weg des Springers, der genau einmal über jedes der Felder des Schachbrettes führt.

5. 6. 6 Beispiel: Backtracking n Ansatz eines Algorithmus (in unvollständiger Notation) track (IN: kandidat, OUT: erfolgreich) { trage_ein(kandidat); // erst mal eintragen erfolgreich = false; // Initialisierung if (fertig) erfolgreich = true; // Abbruchfall else // weitersuchen { repeat { wähle. Kandidat(neukandidat); // wie auch immer if (neukandidat) then // es geht weiter track (neukandidat, erfolgreich) // Rekusion else // Sackgasse ! trage_aus (kandidat); // wieder austragen } until (erfolgreich) or (not neukandidat) } }

5. 7 Berechenbarkeit n Wir haben den Begriff und die Elemente eines Algorithmus vorgestellt und Algorithmen zur Lösung von Problemen verwendet. In diesem Unterkapitel werden nun einige Fragen zur Anwendbarund Sinnhaftigkeit von Algorithmen gestellt und beantwortet. n Inhalt: 1. 2. 3. 4. 5. 6. Einige Fragen Das Entscheidungsproblem Die Turing-Maschine Berechenbarkeit Rekursive Funktionen Church‘sche These H. Ernst: “Grundlagen und Konzepte der Informatik“, Vieweg-Verlag, 2000

5. 7. 1 Einige Fragen 1. Kann jedes Problem durch einen Algorithmus beschrieben werden, d. h. prinzipiell - bei genügender Sorgfalt - gelöst werden ? 2. Kann jeder Algorithmus in ein Programm übertragen werden ? n Welchen Anforderungen muss eine Programmiersprache genügen, damit jeder Algorithmus damit formuliert werden kann ? 3. Ist ein Computer grundsätzlich in der Lage, einen bekannten, als Programm formulierten Algorithmus auszuführen ? 4. Ist ein solcher Computer formalisierbar ? n n Wie sieht ein solches abstraktes Model aus ? Gibt es genau ein Model oder mehrere ? Sind diese Modelle äquivalent ? Gibt es andere Modelle oder Beschreibungsformen, diesem formalisierten Computermodell entsprechen ? n Frage 1 und Frage 4 sind wesentlich für den Begriff der Berechenbarkeit, Frage 2 wird im anschließenden Kapitel behandelt, Frage 4 ist Gegenstand der Vorlesung „Compilerbau“

5. 7. 2 Das Entscheidungsproblem n Bis weit ins 20 ste Jahrhundert war die Mehrzahl der Mathematiker (insb. David Hilbert: 1862 -1942) der Ansicht, dass man von jeder Aussage algorithmisch beweisen könne, ob sie wahr oder falsch sein. n Anders ausgedrückt: Es sei entscheidbar, ob ein Problem lösbar oder unlösbar ist. n Die Frage, ob dies entscheibar ist oder nicht ging als Entscheidungsproblem in die Geschichte der Mathematik (und Informatik) ein. n Kurt Gödel wies in seinem Unvollständigkeits-Theorem 1931 nach, dass alle widerspruchsfreien axiomatischen Formulierungen der Zahlentheorie unentscheidbare Aussagen enthalten. n damit wurde insb. belegt, dass streng algorithmisch arbeitende Computer prinzipiell nicht jedes Problem lösen können. n Auf fast schon philosophischer Ebene wurde damit auch belegt, dass Wahrheit eine andere Qualität als Beweisbarkeit besitzt. n nicht alle „wahren“ Aussagen können auch bewiesen werden.

5. 7. 3 Die Turing-Maschine: Definition n Als abstraktes Modell eines Computers beschrieb Alan Turing (19121954) 1963 - also noch vor der Erfindung des Digitalrechners - eine nach ihm benannte abstrakte Maschine n Formal kann eine Turing-Maschine wie folgt beschrieben werden: n Alphabet: A = {a 0, . . . , an}, der Zeichenvorrat der Turing-Maschine, wobei a 0 das Leerzeichen ("blank") darstellt (Oft: a 1=0, a 2=1) n Bandinschrift: B: Z A eine Zuordnung, die jeder Stelle des rechtsseitig unendlichen Bandes ein Zeichen zuordnet. Dabei wird festgesetzt, dass B(k) = a 0 für alle bis auf endlich viele. n Kopfposition: k Z n Zustände: eine endliche Menge von Maschinenzuständen. Q = {q 0, . . . , qm} Darunter sind q 0, der Anfangszustand und H Q , die Menge der Haltezustände, ausgezeichnet. n Turing-Tabelle: eine Übergangsrelation: d : A Q {r, l, n}, das jedem (gelesenen) Zeichen in Abhängigkeit eines Zustandes ein neues Zeichen, einen Folgezustand und eine Aktion (r, l, n} zuordnet

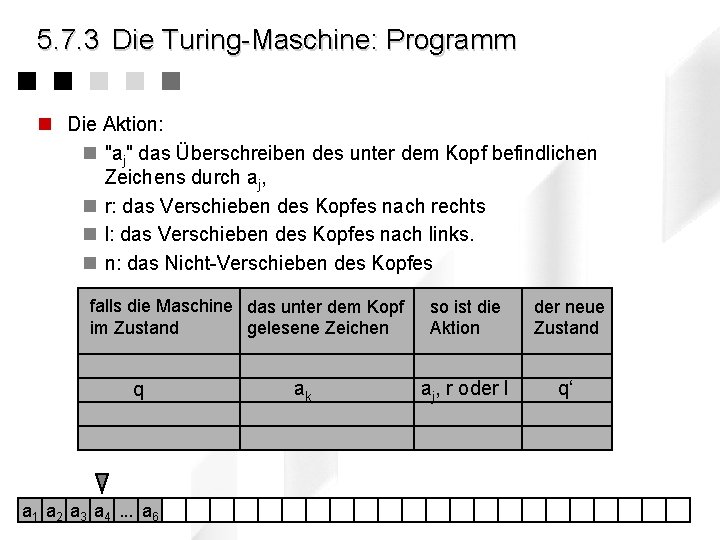
5. 7. 3 Die Turing-Maschine: Programm n Die Aktion: n "aj" das Überschreiben des unter dem Kopf befindlichen Zeichens durch aj, n r: das Verschieben des Kopfes nach rechts n l: das Verschieben des Kopfes nach links. n n: das Nicht-Verschieben des Kopfes falls die Maschine das unter dem Kopf im Zustand gelesene Zeichen q a 1 a 2 a 3 a 4. . . a 6 ak so ist die Aktion der neue Zustand aj, r oder l q‘

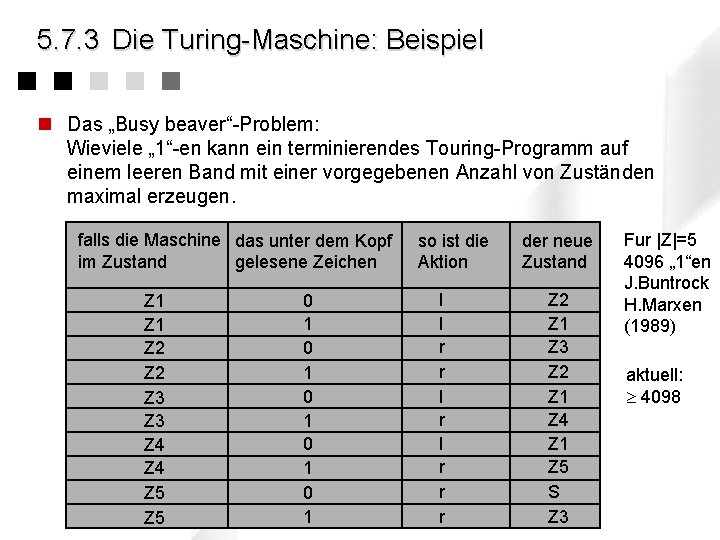
5. 7. 3 Die Turing-Maschine: Beispiel n Das „Busy beaver“-Problem: Wieviele „ 1“-en kann ein terminierendes Touring-Programm auf einem leeren Band mit einer vorgegebenen Anzahl von Zuständen maximal erzeugen. falls die Maschine das unter dem Kopf im Zustand gelesene Zeichen Z 1 Z 2 Z 3 Z 4 Z 5 0 1 0 1 0 1 so ist die Aktion l l r r r der neue Zustand Z 2 Z 1 Z 3 Z 2 Z 1 Z 4 Z 1 Z 5 S Z 3 Fur |Z|=5 4096 „ 1“en J. Buntrock H. Marxen (1989) aktuell: 4098

5. 7. 4 Definition: Berechenbarkeit n Ein Problem ist genau dann algorithisch lösbar, wenn es durch eine Turing-Maschine darstellbar ist. n Eine Funktion f(x) heißt berechenbar, genau dann wenn es einen Algorithmus (eine Turing-Maschine) gibt, der bei gegebenem x das Ergebnis f(x) liefert n Ein Computer ist äquivalent zu einer universellen Turing-Maschine. n d. h. ein Computer ist äquivalent zu einer Turing-Maschine, die jede andere Turing-Maschine simulieren kann. n Zur Simulation einer beliebigen Turing-Maschine muss auf dem Eingabeband eine Beschreibung der zu simulierenden Maschine codiert werden und außerdem deren Eingabeband gespeichert sein. n Die Menge verschiedener universeller Turing-Maschinen ist abzählbar - denn das Band ist binär codiert, jede Kombination lässt sich auf eine natürliche Zahl abbilden. Die Menge aller Funktionen f(x) ist überabzählbar (z. B. Funktionen die auf eine reelle Zahl abbilden) Es gibt (unendlich viele) nicht berechenbare Funktionen

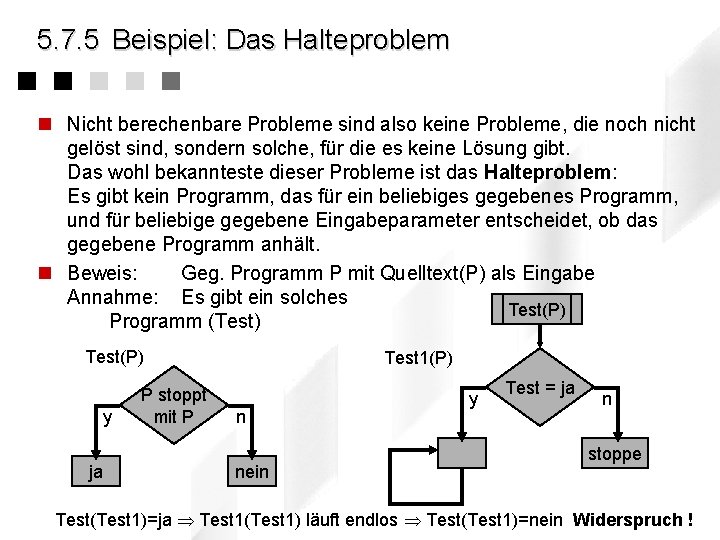
5. 7. 5 Beispiel: Das Halteproblem n Nicht berechenbare Probleme sind also keine Probleme, die noch nicht gelöst sind, sondern solche, für die es keine Lösung gibt. Das wohl bekannteste dieser Probleme ist das Halteproblem: Es gibt kein Programm, das für ein beliebiges gegebenes Programm, und für beliebige gegebene Eingabeparameter entscheidet, ob das gegebene Programm anhält. n Beweis: Geg. Programm P mit Quelltext(P) als Eingabe Annahme: Es gibt ein solches Test(P) Programm (Test) Test(P) y ja P stoppt mit P Test 1(P) n nein y Test = ja n stoppe Test(Test 1)=ja Test 1(Test 1) läuft endlos Test(Test 1)=nein Widerspruch !

5. 7. 6 Rekursive Funktionen n Es gibt innerhalb der mathematischen Funktionen zwei Unterklassen: n primitiv-rekursive Funktionen: l jede primitiv-rekursive Funktion ist berechenbar l es gibt berechenbare Funktionen, die nicht primitiv-rekursiv sind l primitiv-rekursive Funktionen lassen sich genau mit Algorithmen ohne Schleifenkonstrukte (aber mit Blockung) darstellen. n -rekursive Funktionen l jede -rekursive Funktion ist berechenbar l es gibt berechenbare Funktionen, die nicht -rekursiv sind l -rekursive Funktionen lassen sich mit Algorithmen mit Schleifenkonstrukte (und Blockung) darstellen. n Es gilt folgende Beziehung innerhalb von Funktionen: berechenbare Funktionen -rekursive Funktionen primitiv-rekursive Funktionen

5. 7. 6 Church‘sche These n Wir haben bislang verschiedene Äquivalenzen gefunden: n Primitiv und -rekursive Funktionen sind Teilmengen von berechenbaren Funktionen. n Eine Funktion ist genau dann berechenbar, wenn es eine Turing. Maschine zu deren Berechnung gibt, . n Die Darstellung mit Hilfe einer Turing-Maschine ist äquivalent mit der einer universellen Turingmaschinm, die wiederum eine Abstraktion eines Computers darstellt n Dies legt die Formulierung einer der Church‘schen These nahe: Alle im intuitiven Sinn vernünftigen Formalisierungen von Problemlösungen sind äquivalent n Wenn ein Problem nicht durch eine Turing-Maschine gelöst werden kann, so ist es algorithmisch überhaupt nicht lösbar n Da Begriffe wie „intuitiv“ und „vernünftig“ nicht definiert sind, ist die Church‘sche These nicht beweisbar.

5. 8 Korrektheit n Wir haben diskutiert, ob man jede (mathematische) Funktion berechnen kann und haben dabei die Äquivalenz eines Algorithmus‘ mit berechenbaren Funktionen gesehen. In diesem Unterkapitel geht es nicht mehr nur darum, ob eine Funktion berechenbar ist, bzw. ein Algorithmus für deren Berechnung existiert, sondern ob der gegebene Algorithmus tatsächlich das macht, was er machen soll n Inhalt U. Kastens: “Modellierung“, Vorlesung WS‘ 00/‘ 01, Uni Paderborn 1. 2. 3. 4. 5. 6. 7. 8. Ansatz Definition Logik zur Verifikation (C. A. R. Hoare) Regeln Terminierung Beispiele Beweis des Euklid‘schen Algorithmus Kritische Anmerkungen

5. 8. 1 Ansatz n Wir haben zu Beginn des Kapitels den Begriff der Korrektheit definiert: n partielle Korrektheit: Jedes berechnete Ergebnis genügt der Ausgabespezifikation, sofern die Eingaben der Eingabespezifikation genügt haben n Terminierung: Der Algorithmus hält nach endlich vielen Schritten mit einem Ergebnis an, sofern die Eingaben der Eingabespezifikation genügt haben n Zum Beweis der Korrektheit gehen wir also von der Eingabespezifikation aus und versuchen, mit den Aktionen (Statements) des Algorithmus die Ausgabespezifikation abzuleiten. n Die Eingabespezifikation wird dabei als Vorbedingung P(V) oder {P} und die Ausgabespezifikation Q(V) oder {Q} als Nachbedingung mathematisch formuliert n Über die Aktionen des Algorithmus wird die Vorbedingung über Zusicherungen Zi(V) zur Nachbedingung abgeleitet n Also: P(V) Z 1(V) . . . Zn(V) Q(V)

5. 8. 2 Definition: Korrektheit n Beispiel: Lösung der quadratischen Gleichung qugl (IN: p, q: real, OUT x 1, x 2: real) // Vorbedingung: (p*p)/4 > q // Nachbedingung: x 1 = (-b + sqr(p*p/4 -q)) / (2*a) // x 2 = (-b - sqr(p*p/4 -q)) / (2*a) { w : real; w = sqr(p*p/4 - q); x 1 = -p/2 + w; x 2 = -p/2 - w: } n Ein Algorithmus heißt korrekt bezüglich seiner Spezifikation, wenn für jeden Aufruf, der die Vorbedingung erfüllt, nach dem Aufruf des Algorithmus‘ die Nachbedingung erfüllt ist (und er terminiert) n Achtung: Die Vorbedingung ist vom Aufrufer zu erfüllen, die Nachbedingung ist durch den Algorithmus (bzw. den Implementierer) zu erfüllen.

5. 8. 3 C. A. R. Hoare: Logik zur Verifikation n C. A. R. Hoare formulierte 1969 ein Kalkül zum Beweis von Aussagen über Algorithmen und Programme n damit sind - im Gegensatz zum Testes - statische Aussagen über Zustände des Algorithmus ( Werte der Variablen) möglich. Diese Aussagen gelten für alle Ausführungen des Algorithmus n Durch logisch Schlüsse über die Elemente eines Algorithmus kann gezeigt werden, dass n an einer bestimmten Stelle im Algorithmus eine bestimmte Aussage gilt. n eine Aussage an jeder Stelle eines Teils des Algorithmus invariant gilt n Schleifen terminieren. Also: n ein Algorithmus aus jeder zulässigen Eingabe die geforderte Ausgabe berechnet

5. 8. 3 C. A. R. Hoare: Beispiel n min (IN: a, b: integer, OUT min: integer) // Vorbedingung: a, b > 0 (nicht unbedingt notwendig) // Nachbedingung: (min=a min=b) (min a) (min b) { if a<b then { // Z 1: a<b min = a; // Z 2: a<b min=a Z 3: min=a min b } else { // Z 4: b a min = b; // Z 5: b a min=b Z 6: min=b min a } // Z 7: (min=a min b) (min=b min a) // Z 8: (min=a min=b) (min a) (min b) = Q } n Damit ist aus der Vorbedingung P mit Hilfe der Anweisung in min() die Nachbedingung Q formal abgeleitet worden.

5. 8. 3 C. A. R. Hoare: Vorgehen n Aussagen über den Algorithmenzustand, über Werte von Variablen werden in den Algorithmus eingefügt: n { P } A 1 { Q } A 2 { R } n bedeutet: Q gilt immer zwischen der Ausführung von A 1 und der Ausführung von A 2 n Beispiel: { i + 1 0} i : = i + 1; { i 0 } a [i] : = k; {. . . } n Zur Verifikation eines Algorithmus muss für jede Anweisung S ein Nachweis geführt werden: n { Vorbedingung P } S { Nachbedingung Q } n nachweisen: Wenn vor der Ausführung des Schrittes S die P gilt, dann gilt Q nach der Ausführung von S, falls S terminiert. n Beispiel: { i + 1 0} i : = i + 1; {i 0} mit Zuweisungsregel nachweisen n Die Aussagen werden entsprechend der Struktur von S verknüpft. Für jede Anweisungsform wird eine spezielle Schlussregel angewandt. n Die Spezifikation liefert Vorbedingung und Nachbedingung des gesamten Algorithmus:

5. 8. 4 Regel: Zuweisung n Die Zuweisung x = expr wertet den Ausdruck expr aus und weist das Ergebnis der Variablen x zu. Es gilt dann: {P[x/expr]} x : = expr {P} oder {P(x)} x = f(x) {P(f--1(x))} n P[x/expr] steht für die Substitution von x durch expr in P n Die Nachbedingung P erhält man dadurch, dass man jedes Vorkommen von expr in der Vorbedingung durch x (die linke Seite der Zuweisung) ersetzt n Wenn man also zeigen will, dass nach der Zuweisung eine Aussage P für x gilt, muss man zeigen, dass vor der Zuweisung dieselbe Aussage P für expr gilt. n Beispiele: n {a>0} x = a {x>0} n {i+1>0} i=Succ(i) {i>0}: f(x)=Succ, f-1(x)=Pred(x), {P(Pred(x+1)}=(i+1 -1>0) n {i+1>0} i = i+1 {i>0}

5. 8. 4 Regel: Zuweisung - Beispiele n {P[x/expr]} x : = expr {P} n alle Aussagen der Vorbed. für expr, gelten für x in der Nachbedingung Aussagen der Vorb. über x gelten in der Nachbedingung nicht mehr n Die Nachbedingung P erhält man dadurch, dass man jedes Vorkommen von expr in der Vorbedingung durch x ersetzt l ggf ist die Vorbedingung so umzuformen, dass expr explizit Teil der Vorbedingung ist (auf der linken Seite einer Aussage) 1. 2. 3. 4. 5. 6. 7. 8. {y=5} x=y {a>0 x>7} x=a {a>0 z>0} x=a {i+1>0} i=i+1 {i 0} {i+1>0} {i=2} {i+1=3} {z=5} x=1 {x=5} {x>0 x>7} {x>0 z>0} {i>0} i=i+1 {i=3} {z=5 x=1} falsch ! z>0 ist nicht betroffen passend umformen z nicht betroffen, x neu

5. 8. 4 Regel: Konsequenz n Abschwächung der Nachbedingung wenn gilt und dann gilt auch {P} S {R} {Q} {P} S {Q} Beispiel {a+b>0} S {x>0} {X 0} {a+b>0} S {X 0} n Verschärfung der Vorbedingung wenn gilt und dann gilt auch {P} {R] {R} S {Q} {P} S {Q} n Beispiel (Notation: Im Algorithmus können Implikationen in Ausführungsrichtung eingefügt werden) {a+b>0} x = a+b; {x>0} {2*x 0} y = 2 * x {y 0}

5. 8. 4 Regel: Sequenz n Folgendes Schema lässt sich auf eine Sequenz von Aktionen (Statements) anwenden: wenn gilt {P} S {R} und dann gilt auch {R} S 2 {Q} {P} S 1, S 2 {Q} n Beispiel: {x>0 y>0} a = x; {a>0 y>0} b = y; {a>0 b>0} {x>0 y>0} a = x; {a>0 y>0} {a>0 b>0} n Bei trivialen Ableitungen können die Zwischenschritte (Zusicherungen, Aussagen) auch weggelassen werden: {x>0 y>0} a = x; b = y; {a>0 b>0}

5. 8. 4 Regel: Bedingte Anweisung n Schema: wenn gilt und {P B} S {Q} dann gilt auch {P B} {Q} {P} if B then S {Q} n Um die Nachbedingung einer bedingten Anweisung zu beweisen, muss 1. aus der Vorbedingung und der Anweisungs-Bedingung über die Anweisung die Nachbedingung nachgewiesen werden 2. aus der Vorbedingung und der Negation der Anweisung die Nachbedingung direkt folgen n Beispiel: n Gegeben: if a<0 then a = -a n Beweise, dass der Algorithmus a 0 für alle a liefert: 1. {P a<0} {P -a>0} a=-a {P a>0} {P a 0} 2. {P (a<0)} {P a 0} dann gilt auch {P} if a<0 then a=-a {P a 0}

5. 8. 4 Regel: Bedingte Anweisung - Notation n Beispiel: n Gegeben: if a<0 then a = -a n Beweise, dass der Algorithmus a 0 für alle a liefert: 1. {P a<0} {P -a>0} a=-a {P a>0} {P a 0} 2. {P (a<0)} {P a 0} dann gilt auch {P} if a<0 then a=-a {P a 0} n Notation: {P} if a<0 then {P a<0} {P -a>0} a = -a {P a>0} {P a 0} // leere Alternative: {P (a<0)} {P a 0}

5. 8. 4 Regel: Einfache Alternative n Schema: wenn gilt und {P B} S 1 {Q} dann gilt auch {P B} Ss {Q} {P} if B then S 1 else S 2 {Q} n Aus der gemeinsamen Vorbedingung P muss für beide Alternativen dieselbe Nachbedingung Q nachweisbar sein n Beispiel: Gegeben: a>0, b>0, a b und ein Algorithmus (s. u) n Beweise, dass nach den Operationen immer noch gilt: a>o, b>0 {a>0 b>0 a b} if a>b then {a>0 b>0 a b a>b} {b>0 a-b>0} a = a-b; {b>0 a>0} else {a>0 b>0 a b} {a>0 b-a>0} b = b-a; {a>0 b>0}

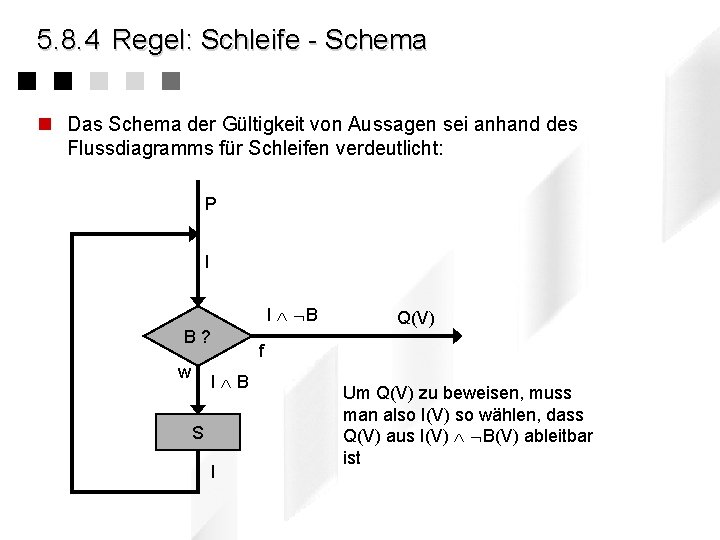
5. 8. 4 Regel: Schleife n Schema: wenn gilt dann gilt auch {P I B} S {P} {I} while B { S } {I B Q} Schleifeninvariante // I = n Schleifeninvarianten sind Zusicherungen in Schleifen, die beim Durchlaufen des Schleifenkörpers erhalten bleiben. Es gelte n n n P Q I B S Zusicherung über Variable vor Schleifeneintritt Zusicherung über Variable nach Schleifenende Schleifeninvariante Wiederholbedingung der Schleife Statements (Aktionen) im Schleifenkörper n Die Nachbedingung einer Schleife ist über die Invariante nachgewiesen nachzuweisen, wenn gilt: n P I die Invariante muss vor Schleifeneintritt wahr sein n (I B) I die Invariante darf in Schleife nicht verändert werden n (I B) Q die Nachbedingung muss sich nach Verlassen der Schleife aus der Invariante nachweisen lassen

5. 8. 4 Regel: Schleife - Schema n Das Schema der Gültigkeit von Aussagen sei anhand des Flussdiagramms für Schleifen verdeutlicht: P I I B B? w I B S I Q(V) f Um Q(V) zu beweisen, muss man also I(V) so wählen, dass Q(V) aus I(V) B(V) ableitbar ist

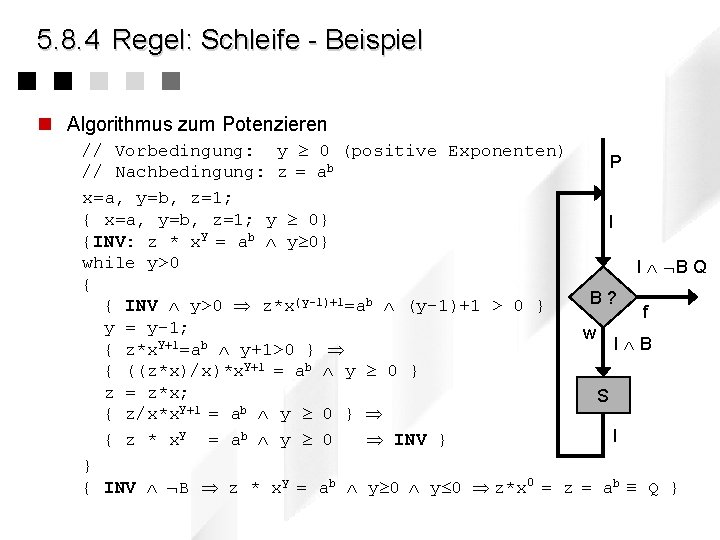
5. 8. 4 Regel: Schleife - Beispiel n Algorithmus zum Potenzieren // Vorbedingung: y 0 (positive Exponenten) P // Nachbedingung: z = ab x=a, y=b, z=1; { x=a, y=b, z=1; y 0} I y {INV: z * x = ab y 0} while y>0 I B Q { B? { INV y>0 z*x(y-1)+1=ab (y-1)+1 > 0 } f y = y-1; w y+1 b I B { z*x =a y+1>0 } { ((z*x)/x)*xy+1 = ab y 0 } z = z*x; S y+1 b { z/x*x = a y 0 } I { z * xy = ab y 0 INV } } { INV B z * xy = ab y 0 z*x 0 = z = ab Q }

5. 8. 4 Regel: Schleife - Schleifeninvariante n Das Finden der „richtigen“ Invariante kann ganz schön kniffelig sein: n Ein paar „Tips“: n Gegeben: Vorbedingung y 0 Zu beweisen: Nachbedingung z = ab n Wenn die Nachbedingung nicht gegeben ist, versuche die Semantik des Algorithmus‘ zu verstehen, z. B. anhand von Beispielen. n Betrachte die Anweisungen in der Schleife: Meist wird etwas vergrößert (z. B. die Variable der Abbruchbedingung), während etwas anderes verkleinert wird - oder umgekehrt. Kombiniere diese: z * xy n Setze Ein- und Ausgabevariablen in Bezug zueinander z * xy = a b n Beachte, dass aus INV und B(V) Q(V) ableitbar sein soll Das bedeutet, dass man die In variante aus der Nachbedingung konstruieren kann, indem man die negierte Bedingung mit berücksichtigt z * xy = ab y=0 z*x 0 = z = ab Q

5. 8. 5 Terminierung n Die Terminierung einer Schleife muss separat nachgewiesen werden n Beweis der Terminierung 1. Gib einen ganzzahligen Ausdruck E an über Variablen, die in der Schleife vorkommen und zeige, dass E bei jeder Iteration durch S verkleinert wird 2. Zeige, dass E nach unten begrenzt ist, z. B. dass 0 E eine Invariante der Schleife ist 3. Zeige, dass die Grenze auch erreicht wird. n E kann nauch monoton vergrößert und nach oben begrenztb sein n Beweis der Nicht-Terminierung: Beweise, 1. dass R B eine Invarianz der Schleife ist (also R in die Schleife geht) und dass es eine Variablenbelegung gibt, so dass R B vor der Schleife gilt 2. dass R einen speziellen Zustand charakterisiert, in dem die Schleife nicht anhält n Es gint Schleifen, für die man nicht entscheiden kann, ob sie für jede Vorbedingung terminieren.

5. 8. 5 Terminierung - Beispiele n { a>0 b>0 } while a b { while a>b { a=a-b } while a<b { b=b-a } } // terminiert n { a>0 b>0 } while a b { a=a-b } while a<b { b=b-a } } // terminiert nicht immer (a = 2*b) n { n n>1 } while n>1 if n gerade then n = n/2 else n=3*n+1 // Terminierung unbewiesen

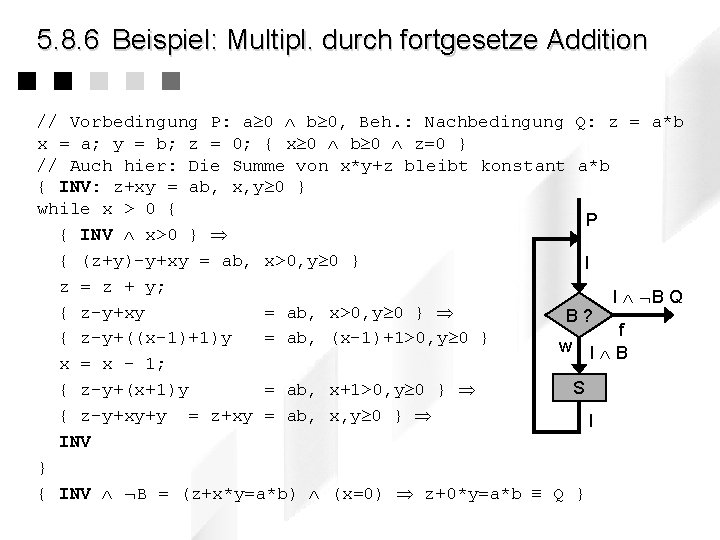
5. 8. 6 Beispiel: Multipl. durch fortgesetze Addition // Vorbedingung P: a 0 b 0, Beh. : Nachbedingung Q: z = a*b x = a; y = b; z = 0; { x 0 b 0 z=0 } // Auch hier: Die Summe von x*y+z bleibt konstant a*b { INV: z+xy = ab, x, y 0 } while x > 0 { P { INV x>0 } { (z+y)-y+xy = ab, x>0, y 0 } I z = z + y; I B Q { z-y+xy = ab, x>0, y 0 } B? f { z-y+((x-1)+1)y = ab, (x-1)+1>0, y 0 } w I B x = x - 1; S { z-y+(x+1)y = ab, x+1>0, y 0 } { z-y+xy+y INV = z+xy = ab, x, y 0 } } { INV B = (z+x*y=a*b) (x=0) z+0*y=a*b Q } I

5. 8. 6 Beispiel: Die ägyptische Bauernmultiplikation // Vorbedingung P: a 0 b 0, Beh. : Nachbedingung Q: z = a*b x = a; y = b; z = 0; { x, y 0 z=0 x=a y=b } // Schleife verdoppelt x und halbiert y: Invariante: INV = { z+x*y = a*b x, y 0 } while x > 0 { { INV x>0 } if (odd(x) then { (z+y)-y+x*y = a*b) x>0, y 0 } z = z+y; { odd(x) z-y+x*y = a*b x>0, y 0 } // leere Anweisung { even(x) z+x*y = a*b x>0, y 0 } { odd(x) z-(2 y/2)+x*(2 y/2) = a*b x>0, (2 y/2) 0 } even(x) z+x*(2 y/2) = a*b x>0, (2 y/2) 0 } y = y * 2; { odd(x) z-y/2+x*y/2 = a*b x>0, y/2 0 even(x) z+x*y/2 = a*b x>0, y/2 0 } { odd(x) z-y/2+(2(x div 2)+1)*y/2 = a*b (2(x div 2)+1)>0, y 0 even(x) z+(2(x div 2))*y/2 = a*b 2(x div 2) >0, y 0 } x = x div 2; // div = Ganzzahldivision { odd(2 x+1) z-y/2+(2 x+1)*y/2 = a*b (2 x+1)>0, y/2 0 even(2 x) z+ 2 x *y/2 = a*b 2 x >0, y/2 0 } { z-(y - y(2 x+1))/2 = z-(y-2 xy-y)/2 = z-(-2 xy/2)= z+xy = a*b z + 2 x * (y*2) = z+xy = a*b } INV } { INV B = (z+x*y=a*b) (x=0) z+0*y=a*b Q }

5. 8. 6 Beispiel: Euklid‘scher Algorithmus (gg. T) // Vorbedingung P: a>0 b 0, Beh. : Nachbed. Q: x=gg. T(a, b) x = a; y = b; // Z 1: x>0 b 0 // Die Summe von x*y+z bleibt konstant a*b { INV: (gg. T(x, y) = gg. T(a, b)) (x>0 y 0) } while y > 0 { { INV (y>0) } r = x mod y; // r ist Rest aus x/y x = y; y = r; { gg. T(y, x mod y) = gg. T(x, y) = gg. T(a, b) } { INV } } // I(A) B(V) = (gg. T(x, y) = gg. T(a, b)) (y=0) // (gg. T(x, 0) = x = gg. T(a, b)) = Q(V)

5. 8. 7 Beweis Euklid‘scher Algorithmus I n Zu beweisen: gg. T(y, x mod y) = gg. T(x, y), x>0, y 0 Der Beweis stützt sich auf einen Hilfssatz, der zunächst bewiesen wird n Hilfssatz: Seien a 0, b. Dann gilt für alle d ( „|“: Ist Teiler von) a) d | a b) d | b d | (a mod b) d | a n Beweis: a) Es sei a mod b = r. Dann ist a - r durch b teilbar. Also ist a - r auch durch d teilbar. Da a durch d teilbar ist, muss auch r durch d teilbar sein, also gilt d | (a mod b). b) Wiederum sei a mod b = r. Dann ist a - r durch b und damit durch d teilbar. Da r durch d teilbar ist, muss auch a durch d teilbar sein, d. h. es gilt d | a.

5. 8. 7 Beweis Euklid‘scher Algorithmus II n Beweis: Es wird gezeigt, dass ggt(a, b) und ggt(b, a mod b) sich gegenseitig teilen und daher gleich sein müssen. 1. Sei d = ggt(a, b). Dann gilt d | a und d | b und nach dem Hilfssatz d | (a mod b) Nach Definition des ggt gilt d | b d | (a mod b) d | ggt(b, a mod b) 2. Sei nun umgekehrt d = ggt(b, a mod b). Dann gilt d | b und d | (a mod b) und nach dem Hilfssatz d | a Nach Definition des ggt gilt d | a d | b d | ggt(a, b) n Mit 1. d=ggt(a, b) | ggt(b, a mod b) und 2. d=ggt(b, a mod b) | ggt(a, b) ist gezeigt, dass ggt(a, b) = ggt(b, a mod b)

5. 8. 8 Kritische Anmerkungen n Die Verifikation entspricht einer mathematischen Beweisführung und kann entsprechend kniffelig, aufwändig, wenn nicht gar unmöglich sein. n Durch formale Überprüfung der Korrektheit, lassen sich Schlüsselstellen eines Algorithmus‘ (eines Programmes) verifizieren n Durch das Denken mit Zusicherungen, Invarianten und mathematische Folgerungen wird die Erstellung fehlerfreier Programme gefördert. n Auch wenn es semi-automatische Systeme zur formalen Verifikation von Algorithmen gibt, ist es praktisch nicht möglich, auch nur halbwegs komplexe Programmsysteme damit zu verifizieren n Selbst wenn es möglich wäre, Algorithmen vollständig formal zu beweisen, so wäre dies keine Garantie, dass ein Programmsystem entsprechend den Wünschen eines „Kunden“ funktioniert. Dazu gehören alle Mechanismen eines ordentlichen Software-Engineerings.