Verschlsselung nach dem RSAVerfahren Adi Shamir Ronald Rivest

Verschlüsselung nach dem RSA-Verfahren Adi Shamir, Ronald Rivest und Leonard Adleman 1977 (von links nach rechts) St. D März, März 2012

Einwegfunktionen Das RSA-Verfahren ist ein rein mathematisches Verfahren und daher nicht so anschaulich darstellbar wie das Vigenère. Verfahren. Der wesentliche Punkt ist die Verwendung von Einwegfunktionen. Darunter sind umkehrbare Funktionen zu verstehen, bei denen die Umkehrfunktion wesentlich schwerer zu berechnen ist, als die Funktion selbst. St. D März, März 2012

Vorüberlegungen St. D März, März 2012

Einwegfunktionen Das Berechnen einer Potenz ist leichter als die Umkehrung mittels des Logarithmus. Ke = G <=> K = loge G e: Exponent (nicht Eulersche Zahl) K: Kodiertes Zeichen des Klartextes, z. B: 65 für A (ASCII) G: Kodiertes Zeichen des Geheimtextes St. D März, März 2012

Einwegfunktionen Ist ein multiplikativ Inverses d des Exponenten e bekannt (d · e = 1), so ist die Berechnung von K aus G dagegen sehr einfach. Gd = (Ke) d = Ke·d = K 1 = K Die (schwierige) Berechnung von K aus G mit Hilfe des Logarithmus wurde ersetzt durch die einfachere Potenzierung mit dem (geheimen) Wert d. St. D März, März 2012

Einwegfunktionen Das Grundprinzip einer assymetrischen Verschlüsselung ist gefunden: Verschlüsseln durch Potenzieren mit dem öffentlichen Schlüssel e: G = Ke Entschlüsseln durch Potenzieren mit dem geheimen Schlüssel d: Gd = K St. D März, März 2012

Einwegfunktionen Wichtig ist dabei natürlich, dass es praktisch unmöglich ist § die Umkehrung der Verschlüsselungsfunktion zu berechnen. § aus dem öffentlichen Schlüssel auf den geheimen Schlüssel zu schliessen. Bei unserem einfachen Beispiel ist das selbstverständlich noch nicht erfüllt. St. D März, März 2012

Verwendung von Divisionsresten Durch die Verwendung von Divisionsresten, sogenannter modulo-Operationen kann das Ziel der praktischen Unumkehrbarkeit erreicht werden. Beispiel: Wähle zwei Zahlen, z. B. 8 und 7. Multipliziere die beiden Zahlen Bilde den Rest bei Division durch 10. Versuche nun aus dem Ergebnis 6 auf die beiden ursprünglichen Zahlen zu schliessen. (8 * 7 ) mod 10 = 6 6 = (2 * 3 ) mod 10 6 = (4 * 9 ) mod 10 6 = (8 * 7 ) mod 10 6 = (23 * 2 ) mod 10 6 = (11 * 6 ) mod 10 6 = (12 * 113 ) mod 10 ? St. D März, März 2012

Kombination Die Kombination der beiden Methoden – Potenzierung und modulo-Operationen – führt zu einem sicheren assymetrischen Verfahren. Klett, Informatik 5: „…Während die Berechnung wk. Pub mod (p·q), das sogenannte modulare Potenzieren, etwa 1000 Rechenschritte erfordert, sind für die Umkehrfunktion, das sogenannte diskrete Logarithmieren, bis zu 10100 Schritte erforderlich. “ Wie lange dauern wohl 10100 Schritte bei einer Rate von 1 Milliarde oder sogar 1 Billion Operationen pro Sekunde? St. D März, März 2012

RSA St. D März, März 2012

RSA - 1977 wurde RSA, das erste öffentlich zugängliche asymmetrische Verschlüsselungsverfahren, veröffentlicht. Adi Shamir, Ronald Rivest und Leonard Adleman 2003 (von links nach rechts) Der Name RSA steht für die Anfangsbuchstaben der Familiennamen der drei Mathematiker am MIT (Massachusetts Institute of Technology), Ronald L. Rivest, Adi Shamir und Leonard Adleman, die RSA entwickelten. St. D März, März 2012

RSA Erzeugung der Schlüssel St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Der öffentliche Schlüssel ist das Zahlenpaar (e, N), der private Schlüssel das Zahlenpaar (d, N), wobei N beiden Schlüsseln gleich ist. N: RSA-Modul, e: Verschlüsselungsexponent d: Entschlüsselungsexponent St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Wähle zufällig und stochastisch unabhängig zwei unterschiedliche Primzahlen p und q. (In der Praxis erzeugt man dazu so lange Zahlen der gewünschten Länge und führt mit diesen anschließend einen Primzahltest durch, bis man zwei Primzahlen gefunden hat. ) Beispiel: Zur Demonstration wählen wir die beiden Mersenne-Primzahlen p = 27 -1 = 127 und q = 213 -1 = 8191 (Diese beiden Primzahlen dienen nur der Demonstration und entsprechen nicht den genannten Bedingungen. Sie sind für praktische Anwendung auch viel zu klein. ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Berechne den RSA-Modul N = p·q Im Beispiel: N = 127 · 8. 191 = 1. 040. 257 Berechne die Eulersche φ - Funktion von N: φ (N) = ( p – 1 )·( q – 1 ) Im Beispiel: φ (N) = 126 · 8. 190 = 1. 031. 940 St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Wähle eine zu φ (N) teilerfremde Zahl e, für die gilt 1 < e < φ (N). Aus Effizienzgründen wird e klein gewählt, üblich ist e = 216+1. Kleinere Werte von können zu Angriffsmöglichkeiten führen. Im Beispiel: Zur Demonstration wählen wir e = 1. 013 Willkürliche Wahl einer Primzahl, daher teilerfremd zu φ (N). St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Berechne den Entschlüsselungsexponenten d als multiplikativ Inverses von e bezüglich des Moduls φ (N). Es soll also gelten: e · d = 1 mod φ (N) Die Berechnung erfolgt mit Hilfe des erweiterten Euklidischen Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 gelten: + 92 307 = 3 * 92 + 31 92 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 30 Die Berechnung = 30 * 1 + 0 Hilfe des erweiterten Euklidischen erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 30 Die Berechnung = 30 * 1 + 0 Hilfe des erweiterten Euklidischen erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des erweiterten Euklidischen erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt + mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: 1 = -10 * 706 + 23 * (e - 1 * 706 ) e · d + k · φ (N) = 1 = gg. T( e, φ (N) ) (wg. Teilerfremdheit) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: 1 = -10 * 706 + 23 * (e - 1 * 706 ) e · d + k · 1φ =(N) gg. T( e, φ (N) ) (wg. Teilerfremdheit) 23 =* e 1 -=33 * 706 konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: 1 = -10 * 706 + 23 * (e - 1 * 706 ) e · d + k · 1φ =(N) gg. T( e, φ (N) ) (wg. Teilerfremdheit) 23 =* e 1 -=33 * 706 1 = 23 * e - 33 * (φ (N) - 1018 * e ) konkret: 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: 1 = -10 * 706 + 23 * (e - 1 * 706 ) e · d + k · 1φ =(N) gg. T( e, φ (N) ) (wg. Teilerfremdheit) 23 =* e 1 -=33 * 706 1 = 23 * e - 33 * (φ (N) - 1018 * e ) konkret: 1 = - 33 * φ (N) + 33617 * e 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Erweiterter Euklidischer Algorithmus: Fortgesetzte Division mit Rest: Berechne d als multiplikativ φ (N) = 1018 den * e Entschlüsselungsexponenten + 706 Erweiterter Euklidischer Algorithmus: e Inverses = 1 *von 706 e bezüglich + 307 des Moduls φ (N). 706 Es soll = 2 also * 307 Bestimmung der Linearkombination: gelten: + 92 307 = 3 * 92 + 31 92 1 = 1 * 31 - 1 * 30 e ·=d 2=* 131 mod φ (N)+ 30 31 = 1 * 30 +1 1 = 1 * 31 - 1 * (92 - 2 * 31) 30 Die Berechnung = 30 * 1 + 0 Hilfe des 1 = erweiterten -1 * 92 + 3 *Euklidischen 31 erfolgt mit (gg. T = 1 – muss wegen Teilerfremdheit so sein) 1 = -1 * 92 + 3 * (307 - 3 * 92 ) Algorithmus. 1 = 3 * 307 - 10 * 92 1 = 3 * 307 - 10 * (706 - 2 * 307 ) Im Beispiel: 1 = -10 * 706 + 23 * 307 Es muss gelten: 1 = -10 * 706 + 23 * (e - 1 * 706 ) e · d + k · 1φ =(N) gg. T( e, φ (N) ) (wg. Teilerfremdheit) 23 =* e 1 -=33 * 706 1 = 23 * e - 33 * (φ (N) - 1018 * e ) konkret: 1 = - 33 * φ (N) + 33617 * e 1. 013 · d + k · 1. 031. 940 = gg. T(1. 013, 1. 031. 940 ) d St. D März, März 2012

Erzeugung von privatem und öffentlichem Schlüssel Durch Kombination der Zahlen e und d mit dem RSA-Modul N können die Schlüssel gebildet werden: Der öffentliche Schlüssel (public key) ist das Zahlenpaar (e, N) Der private Schlüssel (private key) ist das Zahlenpaar (d, N) Im Beispiel: public key: private key: (1. 013, 1. 040. 257) (33617, 1. 040. 257) St. D März, März 2012

Sicherheit Das RSA-Modul N ist als Teil des öffentlichen Schlüssels allgemein bekannt. Wäre es nun leicht möglich, N in seine beiden Primfaktoren zu zerlegen, wäre die Berechnung des geheimen Schlüssels kein Problem. Die Sicherheit des Verfahrens steht und fällt daher mit der Möglichkeit bzw. Unmöglichkeit Primfaktorisierungen effizient zu berechnen. St. D März, März 2012

RSA Kodierung St. D März, März 2012

Aufbereitung des Klartexts Der Klartext muss in Zahlen umgesetzt werden. Geeignet ist z. B. der ASCII-Code (A: 65, B: 66, …. ). Klartext: FKG, WÜRZBURG Aufbereitung: F K G W U E R Z B U R G Umsetzung: 707571878569829066858271 Aufspaltung: 707571 878569 829066 858271 65: 66: 67: 68: 69: 70: 71: 72: 73: 74: 75: 76: 77: 78: 79: 80: 81: 82: 83: 84: 85: 86: 87: 88: 89: 90: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z St. D März, März 2012

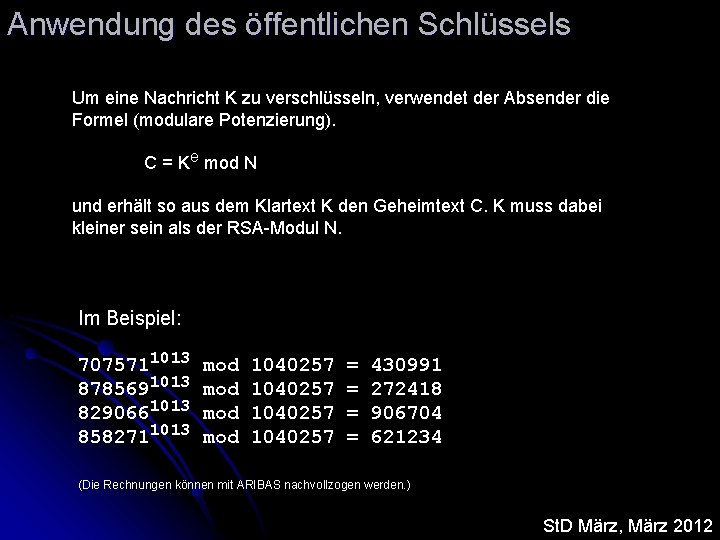
Anwendung des öffentlichen Schlüssels Um eine Nachricht K zu verschlüsseln, verwendet der Absender die Formel (modulare Potenzierung). C = Ke mod N und erhält so aus dem Klartext K den Geheimtext C. K muss dabei kleiner sein als der RSA-Modul N. Im Beispiel: 7075711013 8785691013 8290661013 8582711013 mod mod 1040257 = = 430991 272418 906704 621234 (Die Rechnungen können mit ARIBAS nachvollzogen werden. ) St. D März, März 2012

Interpretation des Geheimtext: 430991 272418 906704 621234 Der Geheimtext stellt keinen Text im eigentlichen Sinne dar. So ist z. B. 09 kein druckbares Zeichen. ASCII-Codes unter 32 stellen Steuerzeichen z. B. für die Ansteuerung eines Druckers dar. 09 entspricht einem Tabulator, ein Drucker wurde also einen Tabulatorsprung machen. Weitere: 10 Line. Feed, 13 Carriage. Return etc. Der Geheim"text" ist also lediglich ein Datenstrom, ein Bitmuster. St. D März, März 2012

RSA Dekodierung St. D März, März 2012

Entschlüsseln mit dem privaten Schlüssel Der Geheimtext C kann durch modulare Potenzierung wieder zum Klartext K entschlüsselt werden. Der Empfänger benutzt die Formel K = Cd mod N mit dem nur ihm bekannten Wert d sowie N. Im Beispiel: 43099133617 27241833617 90670433617 62123433617 mod mod 1040257 = = 707571 878569 829066 858271 (Die Rechnungen können mit ARIBAS nachvollzogen werden. ) St. D März, März 2012

Rekonstruktion des Klartextes Das Bitmuster 707571 878569 829066 858271 wird in zweistellige Zahlen aufgeteilt und mittels ASCII-Code wieder als Text geschrieben. Geheimtext: 707571 878569 829066 858271 Aufbereitung: 70 75 71 87 85 69 82 90 66 85 82 71 Umsetzung: F Klartext: FKG, WÜRZBURG K G W U E R Z B U R G 65: 66: 67: 68: 69: 70: 71: 72: 73: 74: 75: 76: 77: 78: 79: 80: 81: 82: 83: 84: 85: 86: 87: 88: 89: 90: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z St. D März, März 2012

RSA Assymetrie St. D März, März 2012

„Entschlüsseln“ mit dem öffentlichen Schlüssel Die Anwendung des öffentlichen Schlüssels zu einem Entschlüsselungsversuch, etwa mittels K = Ce mod N führt nicht zum Ziel. Im Beispiel: 4309911013 mod 1. 040. 257 = 669392 ergäbe B] statt FKG ! (Die Rechnung kann mit ARIBAS nachvollzogen werden. ) St. D März, März 2012

Sicherheit Das dargestellte Verfahren dient zur Demonstration. Es erfüllt bei Weitem nicht die heutigen Ansprüche an sichere Datenübertragung und wird in der Praxis nicht wie oben beschrieben eingesetzt, da es mehrere Schwächen hat. Mögliche Angriffspunkte und Verbesserungen sind im Artikel "RSA-Kryptosystem" der Wikipedia beschrieben. http: //de. wikipedia. org/wiki/RSA-Kryptosystem St. D März, März 2012