RSA Digital Signature R L Rivest A Shamir












- Slides: 13


數位簽章 ‧RSA Digital Signature (R. L. Rivest, A. Shamir, and L. M. Adleman, 1978) ‧El. Gamal Digital Signature (T. El. Gamal, 1985) ‧Schnorr’s Digital Signature (C. P. Schnorr, 1989) ‧Blind Signature (D. Chaum, 1983) 2

Introduction q Three Basic Services of Cryptography 1. Secrecy (provided by cryptosystems) 2. Authenticity (provided by digital signature scheme) 3. Integrity (provided by digital signature scheme) q Two Famous Digital Signature Schemes 1. RSA Digital signature scheme (based on the factorization problem) 2. El. Gamal digital signature scheme (based on the discrete logarithm) 3

Introduction q Applications: Blind signature (for electronic commerce) 4

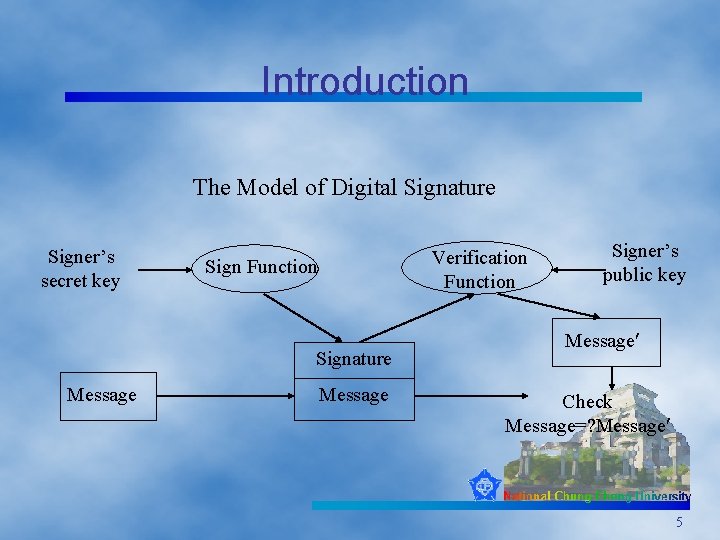
Introduction The Model of Digital Signature Signer’s secret key Verification Function Signature Message Signer’s public key Message Check Message=? Message 5

RSA Public Key Cryptosystem and Digital Signature Scheme q Rivest, Shamir, and Adleman proposed in 1978 q RSA Public Key Cryptosystem ◆ Security Basis: Factorization Problem. ◆ Construction: 1. Choose two large prime numbers P and Q, then compute N=P×Q. 2. Select an integer e such that gcd(e, (N))=1. 3. Compute d such that e×d mod (N)=1. 4. Public key = (N, e). 5. Private key = (P, Q, d). 6

RSA Public Key Cryptosystem and Digital Signature Scheme q RSA Digital Signature Scheme v Sign Function: Signature S=Md mod N. v Verification Function: M=Se mod N. q Example 1. P=11, Q=13, N=143, and (143)=120. 2. e=103, then d=7 (for 103× 7 mod 120=1 ). 3. Sign for M=3: S=37 mod 143=42. 4. Verification: M= Se mod N = 42103 mod 143=3. 7

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q El. Gamal proposed in 1985 q El. Gamal Public Key Cryptosystem ◆ Security Basis: Discrete Logarithm Problem 1. If P is a large prime and g and y are integers, find x such that y=gx mod P. 2. The security restriction on P: P-1 must contain a large prime factor Q. ◆ Construction: 1. Choose a large prime number P and a generator g of GF(P). 2. Private key: a random integer x between 1 and P-1. 3. Public key: y=gx mod P. 8

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q El. Gamal Digital Signature Scheme v Sign Function: Signature (r, s) for message M. 1. Select a random integer k between 1 and P-1 such that gcd(k, P-1)=1. 2. Compute r=gk mod P. 3. Compute s=k-1(M-xr) mod (P-1). v. Verification Function: 1. Verify by checking whether g. M mod P = (rs) ×(yr) mod P. 2. (rs) ×(yr)=g(M-xr) × gxr = g(M-xr)+xr=g. M mod P. 9

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q Example 1. P=23, g=5. 2. x=3, then y=10 (for 53 mod 23=10 ). 3. Sign for the message M=8. 4. Select k=5 between 1 and 22 (P-1). 5. Compute r = gk mod P = 55 mod 23 = 20. 6. Compute s = k-1(M-xr) mod (P-1) = 5 -1(8 -3× 20) mod 22 = 9× 14 mod 22 = 16. 7. Verification: 8. g. M= 58 mod 23 =16 9. (rs)(yr) mod P = 2016 × 1020 mod 23= 13× 3 mod 23 = 16. 10

Schnorr’s Digital Signature Scheme q Schnorr’s Digital Signature Scheme v Sign Function: Signature (r, s) for message M. 1. Select a random integer k between 1 and P-1. 2. Compute r = h(M, gk mod P). 3. Compute s = k + x*r mod (P-1). , where the secret key x the public key y= g-x mod P 4. Send (M, r, s) to the receiver. v. Verification Function: 1. Compute gk mod P=gsyr mod P. 2. Verify by checking whether r = h(M, gk mod P). 11

Blind Signature q D. Chaum proposed in 1983 q D. Chaum’s Blind Signature Scheme ◆ It uses the RSA algorithm. Security Basis: Factorization Problem ◆ Construction: Bob has a public key, e, a private key, d, and a public modulus, N. Alice wants Bob to sign message M blindly. 1. Alice chooses a random integer k between 1 and N. Then she blinds M by computing t = Mke mod N. 2. Bob signs t, td=(Mke)d mod N. 3. Alice unblinds td by computing s=td/k mod N = Md mod N. s is the signature of message M. 12

Blind Signature Property: Untraceable Applications: Blind signature can be used in electronic cash system. Bank 1. t=SN×ke mod N SN: Serial # k: random number 2. t Consumer 4. s=(td)/k mod N=SNd mod N Coin: (SN, s) 3. td mod N 5. Coin -signs coins -database 7. Coin Merchant 6. Verify the signature s 13























