Introduction la logique c Guy Gauthier ing aot

Introduction à la logique (c) Guy Gauthier ing. (août 2001)

Introduction aux fonctions logiques v Systèmes binaires ¤ Deux états fondamentaux et distincts; ¤ Vrai/Faux, Marche/Arrêt, Oui/Non. v Par convention: ¤ Un état est représenté par « 0 » ; ¤ L’autre est représenté par « 1 » . 2

La logique Booléenne v En 1847, George Boole invente une algèbre pour traiter les variables binaires. ¤ Il écrira « The Mathematical Analysis of Logic » , Cambridge, v Il définit 3 opérateurs de base, ainsi qu’une foule de règles et de postulats. 3

Types de représentation v Les fonctions logiques peuvent être représentées de plusieurs façons: ¤ ¤ Équations logiques Tables de vérités Logigrammes Diagrammes échelle (Ladder) v Ces représentations seront introduites avec les fonctions de base. . . 4

Fonctions logiques de base : - NON - ET - OU (c) Guy Gauthier ing. (août 2001)

Fonction logique NON v En anglais: NOT v Représentation: ¤F=A ou F = /A 6

Fonction logique ET v En anglais: AND v Représentation: ¤F=A*B 7

Fonction logique OU v En anglais: OR v Représentation: ¤F=A+B 8

Autres fonctions logiques : - NAND Portes universelles - NOR - EXOR - ID (EXNOR) -. . . (c) Guy Gauthier ing. (août 2001)

Fonction logique NON-ET v En anglais: NAND v Représentation: ¤F=A*B 10

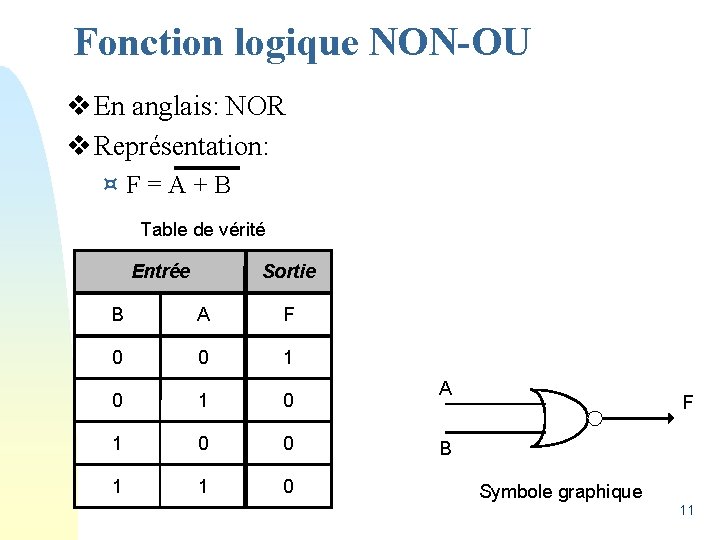
Fonction logique NON-OU v En anglais: NOR v Représentation: ¤F=A+B Table de vérité Entrée Sortie B A F 0 0 1 0 1 0 0 1 1 0 A F B Symbole graphique 11

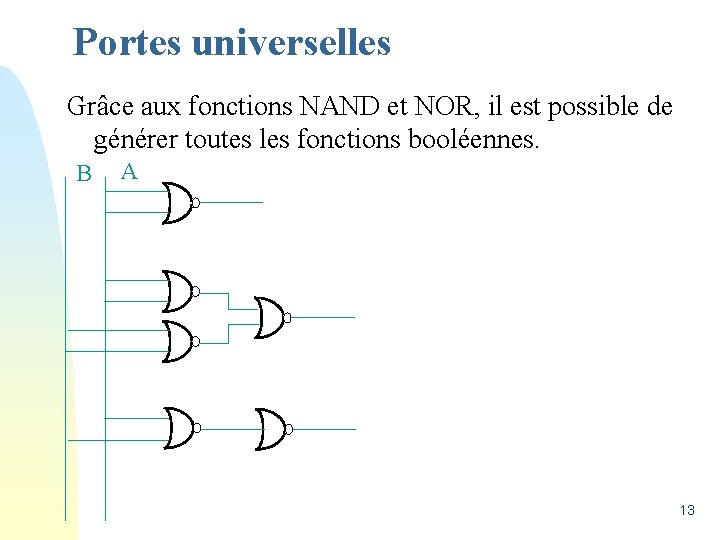
Portes universelles Grâce aux fonctions NAND et NOR, il est possible de générer toutes les fonctions booléennes. A v Ex. Avec NOR NON /(A+A) = /A A+B B ET /(/A +/B) = //A * //B = A*B OU /(/(A +B)) = A +B 12

Portes universelles Grâce aux fonctions NAND et NOR, il est possible de générer toutes les fonctions booléennes. B A 13

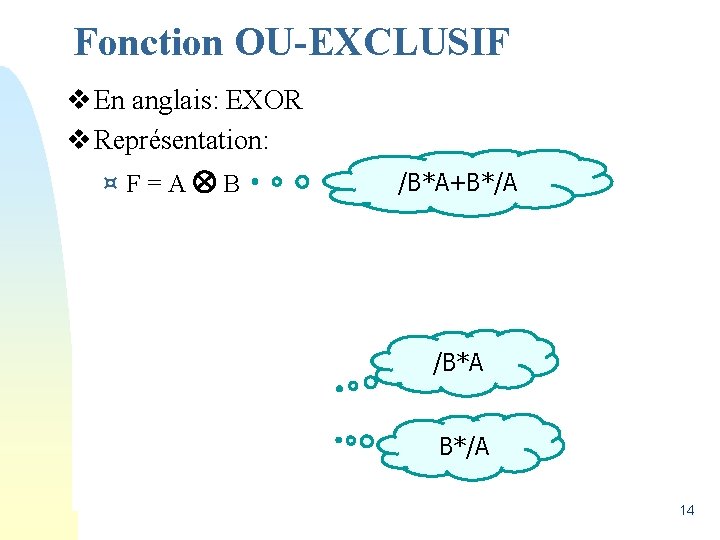
Fonction OU-EXCLUSIF v En anglais: EXOR v Représentation: ¤F=A B /B*A+B*/A /B*A B*/A 14

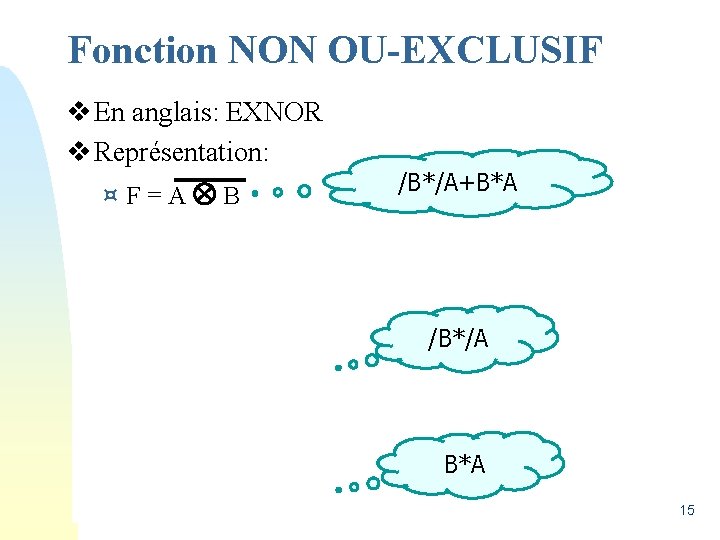
Fonction NON OU-EXCLUSIF v En anglais: EXNOR v Représentation: ¤F=A B /B*/A+B*A /B*/A B*A 15

Fonctions de 2 variables v Il existe 16 fonctions logiques possibles ayant 2 variables. 16

Fonctions de 2 variables F 0 = 0 F 1 = /A. /B F 3 = /A F 2 = /A. B F 5= /B F 4 = A. /B F 7=/(AB) F 6=A B 17

Réalisations des fonctions logiques : - circuit électrique - relais (automatisme) - logigramme (carte de contrôle, circuit intégré, . . . ) (c) Guy Gauthier ing. (août 2001)

Fonction logique NON v Interrupteur normalement fermé 19

Fonction logique ET v Utilise deux interrupteurs normalement ouvert en séries. 20

Fonction logique OU v Utilise deux interrupteurs normalement ouvert en parallèles. 21

Fonction logique NON-ET v Utilise deux interrupteurs normalement fermés en parallèles. 22

Fonction logique NON-OU v Utilise deux interrupteurs normalement fermés en série. 23

Fonction OU-EXCLUSIF v Utilise deux interrupteurs à deux contacts 24

Fonction NON OU-EXCLUSIF v Utilise deux interrupteurs à deux contacts 25

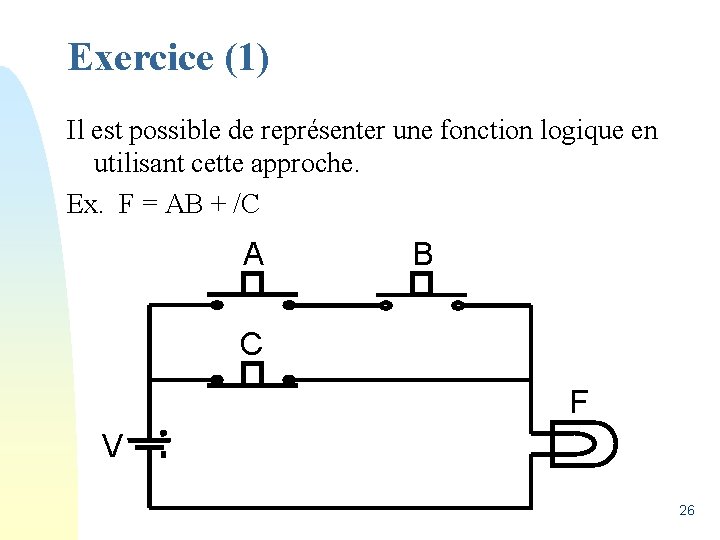
Exercice (1) Il est possible de représenter une fonction logique en utilisant cette approche. Ex. F = AB + /C A B C F V 26

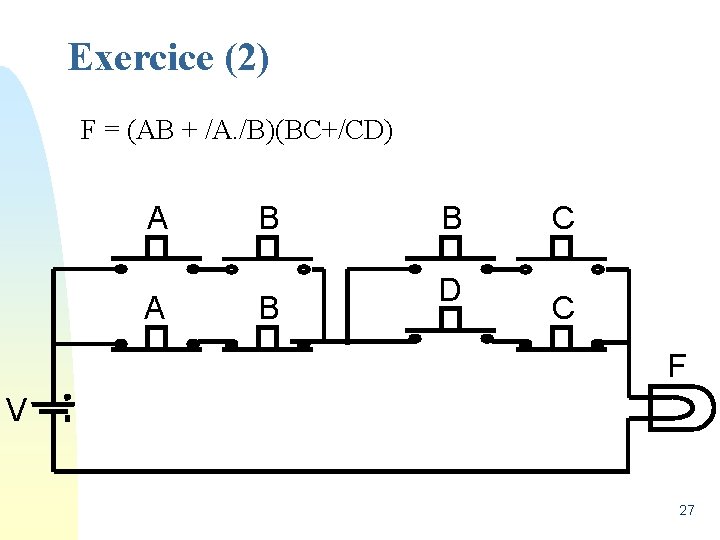
Exercice (2) F = (AB + /A. /B)(BC+/CD) A A B B B D C C F V 27

Réalisations des fonctions logiques : - circuit électrique - relais (automatisme) - logigramme (carte de contrôle, circuit intégré, . . . ) (c) Guy Gauthier ing. (août 2001)

Fonctions logiques utilisant des relais v En automatisation, on utilise les relais pour réaliser des fonctions logiques. v Le relais est une composante électromécanique. A A A 29

Fonction logique NON v Relais avec un contact normalement fermé 30

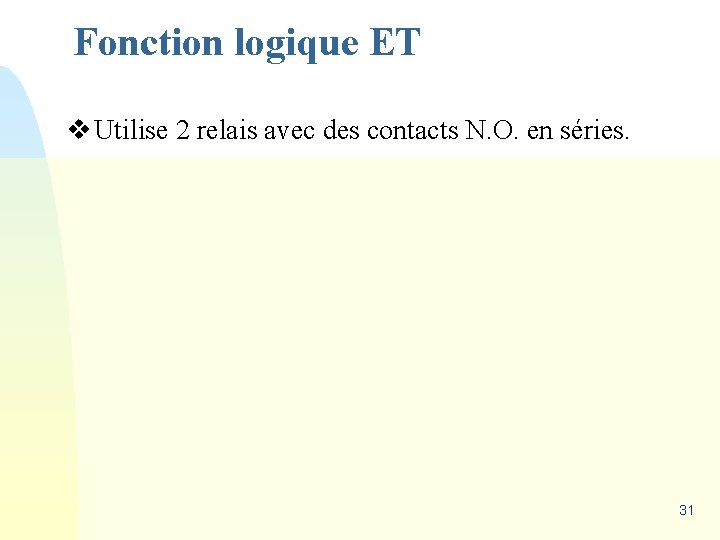
Fonction logique ET v Utilise 2 relais avec des contacts N. O. en séries. 31

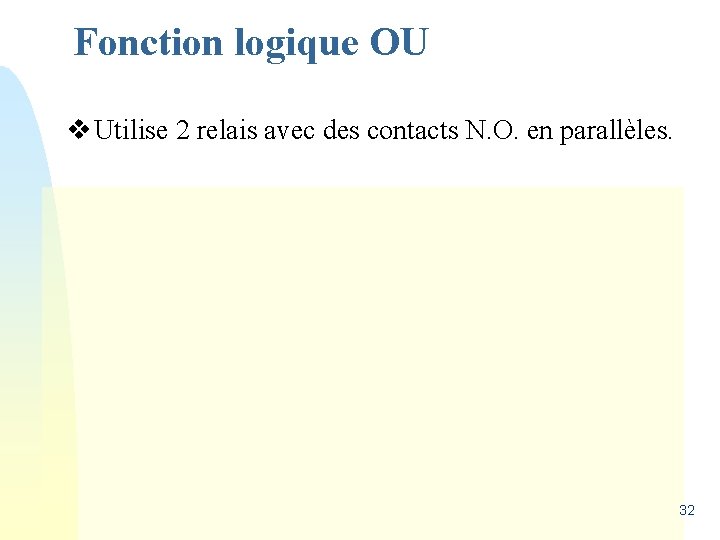
Fonction logique OU v Utilise 2 relais avec des contacts N. O. en parallèles. 32

Fonction logique NON-ET v Utilise 2 relais avec des contacts N. F. en séries. 33

Fonction logique NON-OU v Utilise 2 relais avec des contacts N. F. en parallèles. 34

Fonction OU-EXCLUSIF v Lampe = K L = /K. L + K. /L 35

Fonction NON OU-EXCLUSIF v Lampe = M N = M. N + /M. /N 36

Réalisation : exercice Réaliser (avec des circuits électriques et relais) : - F = ab + c - F = (ab + /a/b)(bc + /cd) - F = (a + b +c)(/a + b/c + c) 37

L ’ALGEBRE DE BOOLE Un ensemble E possède une structure d'algèbre de Boole s'il est muni de deux lois de composition interne associatives et commutatives notées + et * : · les lois + et * sont distributives l'une par rapport à l'autre et admettent un élément neutre (0 et 1 respectivement); · tout élément de E est idempotent pour chaque loi : x + x = x et x • x = x · Tout élément x de E possède un unique élément, dit complémenté de x, généralement noté généralement /x , vérifiant la loi du tiers exclu : x + /x = 1 et le principe de contradiction x * /x = 0. Dans cette algèbre, on peut écrire : /x = 1 - x. 38

L’algèbre Booléenne : lois fond. + et * sont deux lois de composition interne : v Fermeture: ¤ Si A et B sont des variables Booléennes, alors A+B, A*B sont aussi des variables Booléennes. v Commutativité ¤A+B= B+A ¤A*B = B*A 39

L’algèbre Booléenne : lois fond. v Associativité ¤ A + (B + C) = (A + B) + C ¤ A * (B * C) = (A * B) * C v Distributivité ¤ ET sur OU: A(B + C) = AB + AC ¤ OU sur ET: A+(B*C) = (A+B)*(A+C) 2+(3*2) (2*3) + (2*2) 40

L’algèbre Booléenne v Idempotence ¤A+A = A ¤A*A=A v Complémentarité ¤A+A=1 ¤A*A=0 ¤A=A 41

L’algèbre Booléenne v Identités remarquables ¤ 1+A=1 ¤ 0+A=A et et 1*A=A 0*A=0 v Distributivité interne (très utile pour la simplification algébrique des fonctions booléennes). ¤ A + (B + C) = (A + B) + (A + C) ¤ A * (B * C) = (A * B) * (A * C) 42

L’algèbre Booléenne Théorème de De Morgan (A + B) = A * B et A*B=A+B 43

L’algèbre Booléenne : théorèmes Le complément d’une expression quelconque s’obtient en complémentant les variables et en permutant les opérateurs ET et OU. 44

Simplification Méthode algébrique : Appliquer les principes de l’algèbre de Boole. Méthodes graphiques : Karnaugh Mahoney Méthodes programmables : Utilisation des algorithmes de simplification algébrique. 45

Règles de simplification Règle 1 : On peut simplifier une fonction logique en regroupant des termes à l’aide des théorèmes. ABC + AB/C + A/BCD = = AB(C + /C) + A/BCD = AB + A/BCD = A(B + /BCD) Distributivité + / * = A[(B +/B) (B+CD)] = A[(B+CD)] Règle 2 : On peut ajouter un terme déjà existant à une expression logique. ABC + /ABC + A/BC + AB/C = = [ABC + /ABC] + [ABC + A/BC] + [ABC + AB/C] = BC + AB 46

L’algèbre Booléenne : simplification X = X/Y + XY = (X+ Y)(X + /Y) X = X + XY = X(X+Y) X + /XY= X + Y X(/X +Y) = XY XY + /XZ + YZ = XY + /XZ (X+Y)(/X+Z)(Y+Z) = (X+Y)(/X+Z) XY + X/YZ = XY +XZ (X + Y)(X + /Y + Z) = (X+Y)(X+Z) …/. . . 47

L’algèbre Booléenne : expression avec des fonctions NAND et NOR Re-écrire l ’expression de la fonction Z en n ’utilisant : - que des portes NOR, et puis - que des portes NAND (après simplification). Z = (x + /y + z)(x + /z) (/x + /y) 48

Représentations d’une fonction logique Table de vérité Equation logique 49

Table de vérité vs logigrammes v Pour une table de vérité donnée, nous pouvons trouver l’équation logique et le logigramme (ou diagramme échelle) correspondant v Il faut utiliser l’algèbre de Boole pour simplifier. 50

Table de vérité vs logigrammes v Construction d’une table de vérité ¤ ¤ N variables N+1 colonnes 2^N lignes Chaque ligne est représentative d’une combinaison des variables parmi les 2^N possibles (N colonnes). 51

Table de vérité vs logigrammes Exercice. Soit un local ayant trois portes identifiées a, b et c. À proximité de chacune de ces portes nous trouvons un interrupteur à bascule que les gens manipuleront lorsqu’ils entreront ou sortiront. Ces interrupteurs commandent une ampoule qui éclaire le local. Ainsi, une personne qui entre par la porte “ a ” manipulera l’interrupteur “ a ” pour allumer l’ampoule et cette même personne sortant par la porte “ b ” manipulera l’interrupteur “ b ” pour éteindre l’ampoule. Lors de l’inauguration du local, a = 0, b = 0, c = 0, et l’ampoule L est éteinte (L = 0). 52

Formes canoniques des équations booléennes v 1° forme : Somme de produits. F=ABC + B v 2° forme : Produit des sommes. F = (A+B)(A+C) v 3° forme : n’utilise que des NAND F = ABC * ABC v 4° forme : n’utilise que des NOR ¤ F = (A+B+C)+(A+B+C) Ex. Mettre sous la forme 3 l’expression F=ABC+ ABC Ex. Mettre sous la forme 4 l’expression F=(A+B+C) 53

Table de vérité Eq. logique v Trouver l’équation de S. ( ) 54

Exemple v Solution: ¤ On construit l’équation de S en écrivant tous les termes donnant S=1. ¤ Ainsi, S = 1: si C=0 et B=1 et A=0; Ø ou si C=0 et B=1 et A=1; Ø ou si C=1 et B=0 et A=1; Ø ou si C=1 et B=1 et A=0. Ø 55

Exemple v On peut donc écrire: ¤ S = /C. B. /A + /C. B. A + C. /B. A + C. B. /A v On peut simplifier: ¤ S = /C. B + B. /A + C. /B. A v Autre solution possible: ¤ S = /C. B + C. (A B) 56

Si nous utilisions des relais. . . v S = /C. B + B. /A + C. /B. A = B. (/C + /A) + C. /B. A 57

La simplification des équations v La simplification est essentielle. ¤ Il faut avoir le circuit le plus simple que possible. . . v La simplification peut être un processus long si le système est complexe. v Heureusement, il existe des techniques simples pour simplifier. 58

Méthodes de simplification v Il est possible d ’obtenir directement une équation sous sa forme simplifiée en utilisant une méthode de simplification graphique. v Méthodes de simplification graphique: ¤ Tables de Karnaugh ¤ Table de Mahoney 59

Principes de base v Représentation de la table de vérité sous forme graphique. v Nombre de cases = nombre de lignes de la table de vérité. ¤ Multiple de 2 n (1, 2, 4, 8, 16, . . . ), n = Nombre d ’entrées v Principe de simplification : Deux termes se simplifient s’ils ne diffèrent que par le fait qu’une variable est présente dans un terme et son inverse dans l’autre terme. A/B + AB = A v On cherche à mettre en évidence les simplifications possibles (les termes adjacents). 60

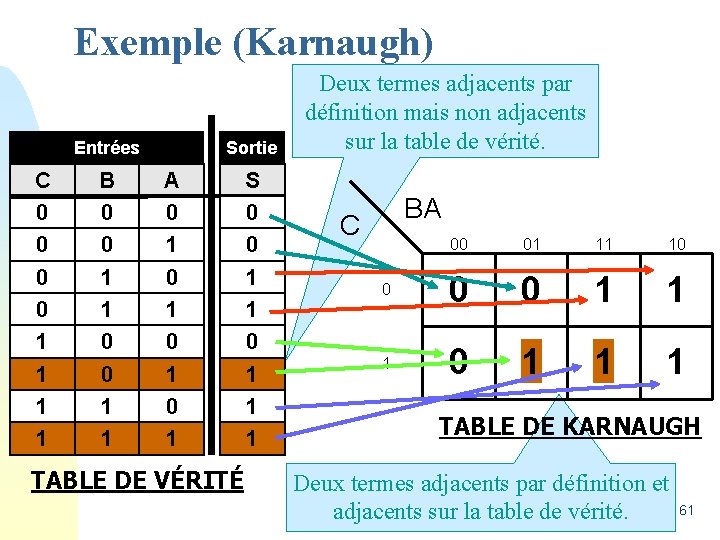
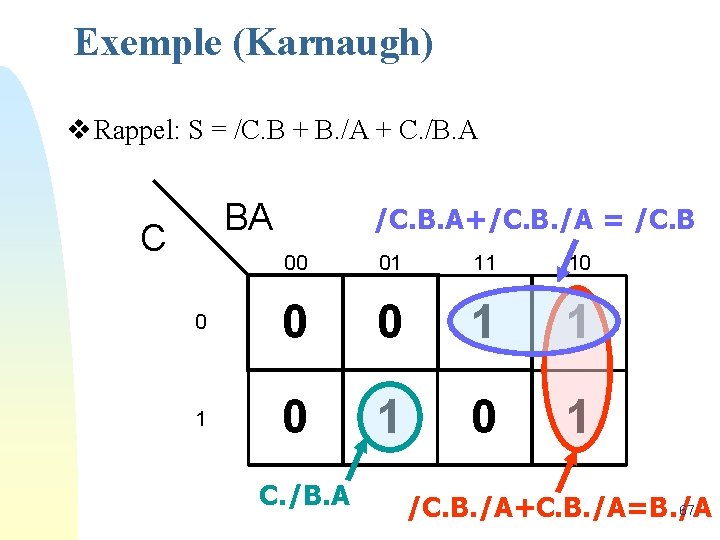
Exemple (Karnaugh) Entrées C 0 0 1 1 B 0 0 1 1 Sortie A 0 1 0 1 TABLE DE VÉRITÉ S 0 0 1 1 1 Deux termes adjacents par définition mais non adjacents sur la table de vérité. BA C 00 01 11 10 0 1 1 1 TABLE DE KARNAUGH Deux termes adjacents par définition et adjacents sur la table de vérité. 61

Principes de base (suite) v À partir de la table, on simplifie en groupant des 1 adjacents. v La taille d’un groupe est un multiple de 2 k (1, 2, 4, 8, . . . ). v Le groupe est soit rectangulaire ou carré. v Former les plus gands groupes possibles (Termes plus simples). v Un 1 peut faire partie de plusieurs groupes. 62

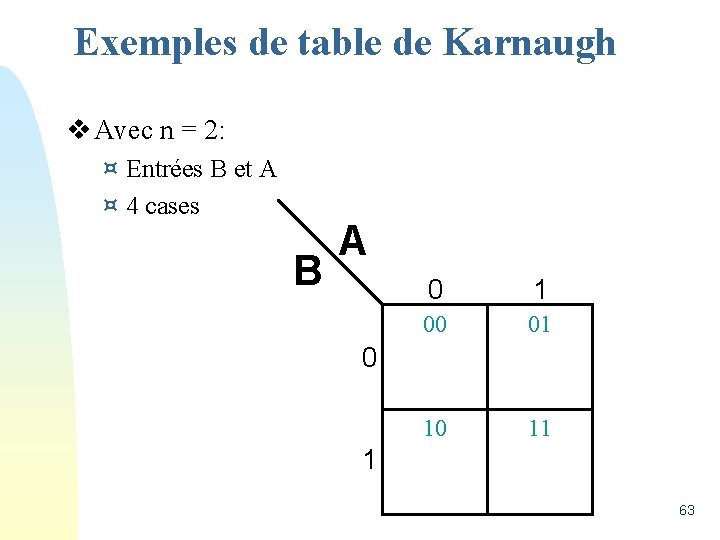
Exemples de table de Karnaugh v Avec n = 2: ¤ Entrées B et A ¤ 4 cases B A 0 1 00 01 10 11 0 1 63

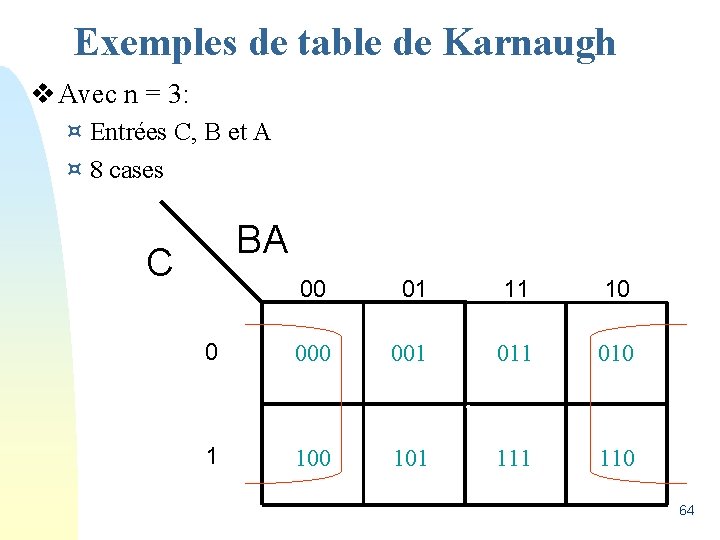
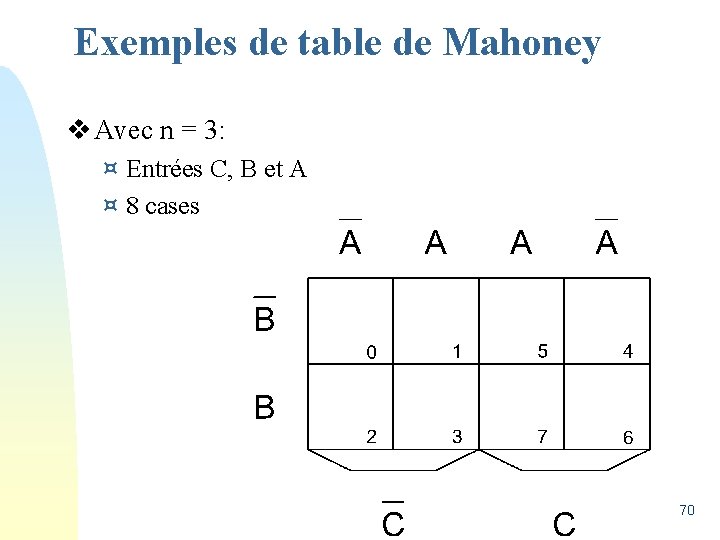
Exemples de table de Karnaugh v Avec n = 3: ¤ Entrées C, B et A ¤ 8 cases BA C 00 01 11 10 0 001 010 1 100 101 110 64

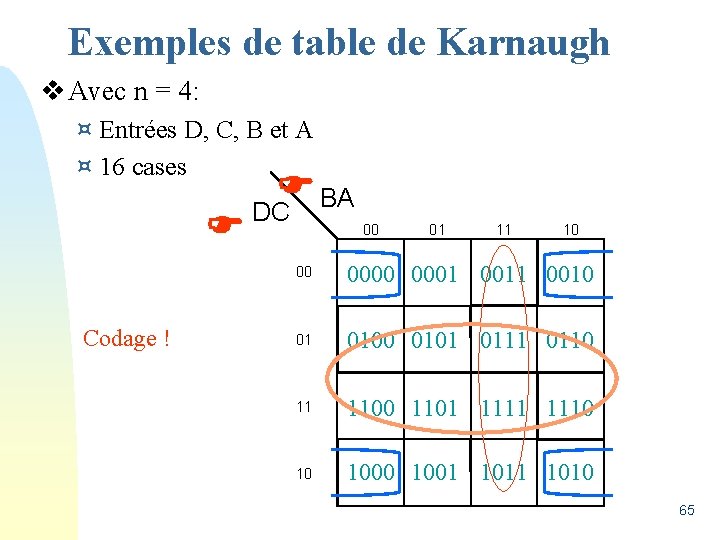
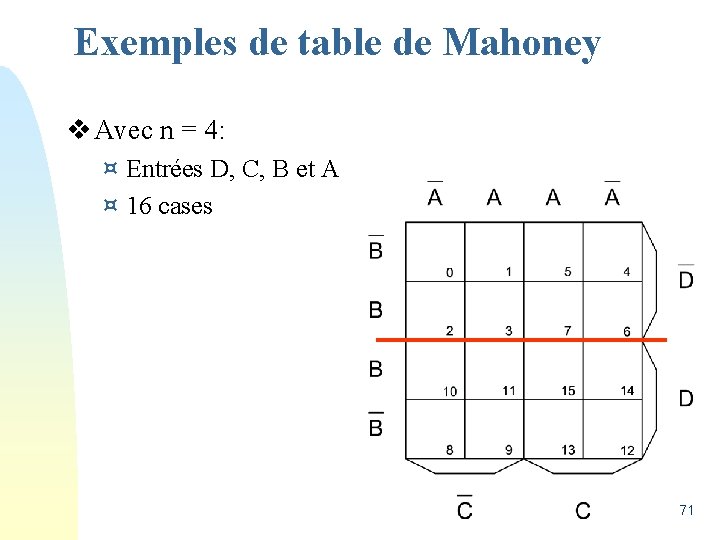
Exemples de table de Karnaugh v Avec n = 4: ¤ Entrées D, C, B et A ¤ 16 cases Codage ! BA DC 00 01 11 10 00 0001 0010 01 0100 0101 0110 11 1100 1101 1110 10 1001 1010 65

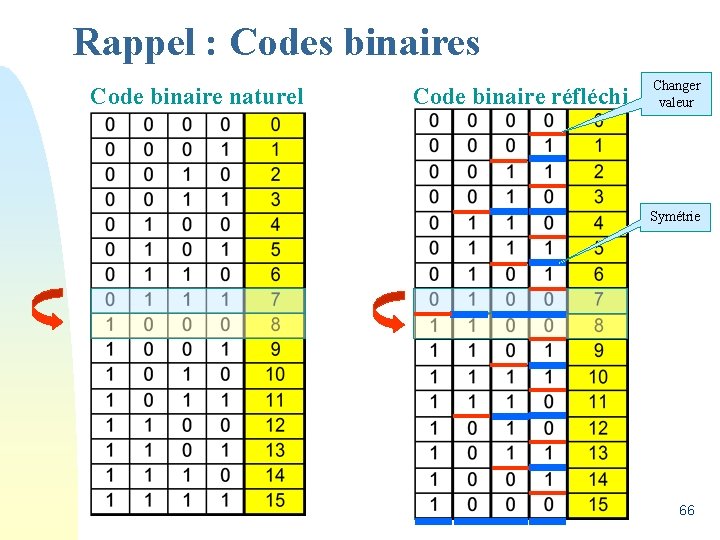
Rappel : Codes binaires Code binaire naturel Code binaire réfléchi Changer valeur Symétrie 66

Exemple (Karnaugh) v Rappel: S = /C. B + B. /A + C. /B. A BA C /C. B. A+/C. B. /A = /C. B 00 01 11 10 0 1 1 1 0 1 C. /B. A 67 /C. B. /A+C. B. /A=B. /A

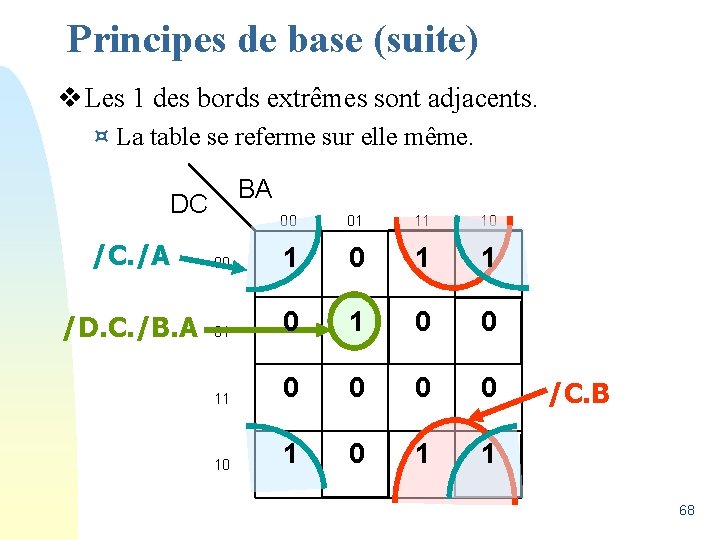
Principes de base (suite) v Les 1 des bords extrêmes sont adjacents. ¤ La table se referme sur elle même. BA DC 00 01 11 10 /C. /A 00 1 1 /D. C. /B. A 01 0 0 11 0 0 10 1 1 /C. B 68

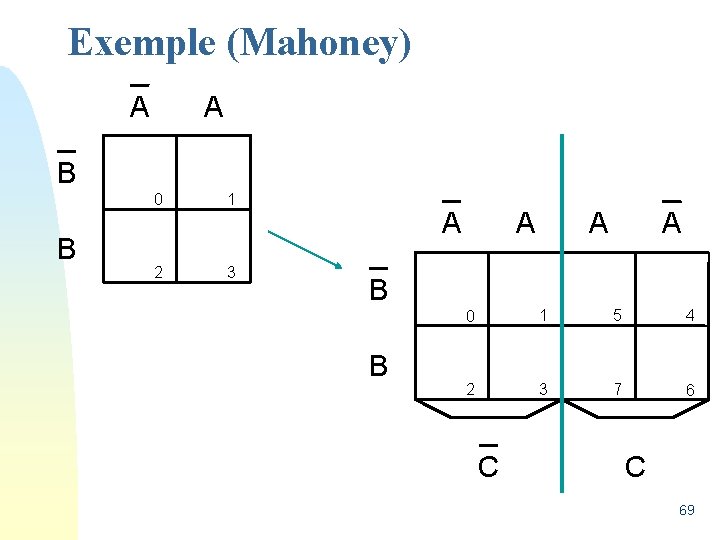
Exemple (Mahoney) A A B B 0 1 2 3 A A B B 0 1 5 4 2 3 7 6 C C 69

Exemples de table de Mahoney v Avec n = 3: ¤ Entrées C, B et A ¤ 8 cases 70

Exemples de table de Mahoney v Avec n = 4: ¤ Entrées D, C, B et A ¤ 16 cases 71

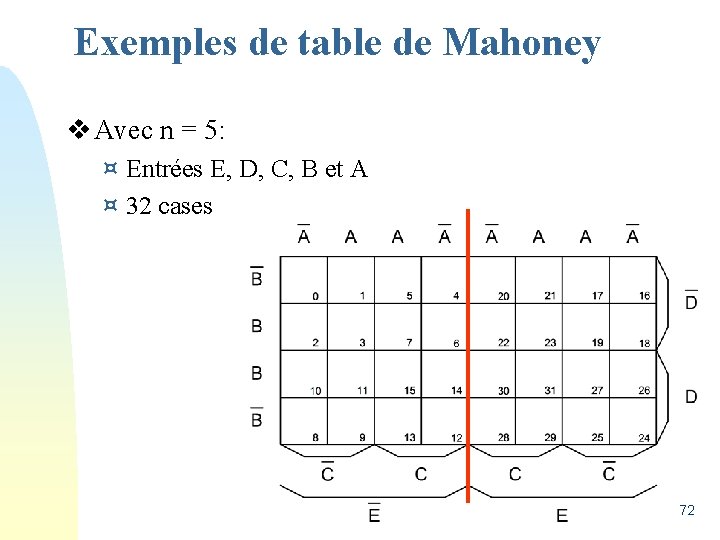
Exemples de table de Mahoney v Avec n = 5: ¤ Entrées E, D, C, B et A ¤ 32 cases 72

Exemples de table de Mahoney v Avec n = 6: 73

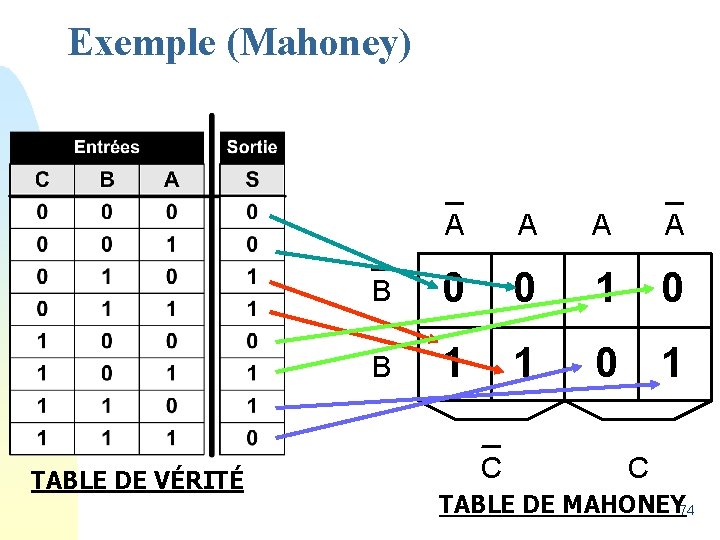
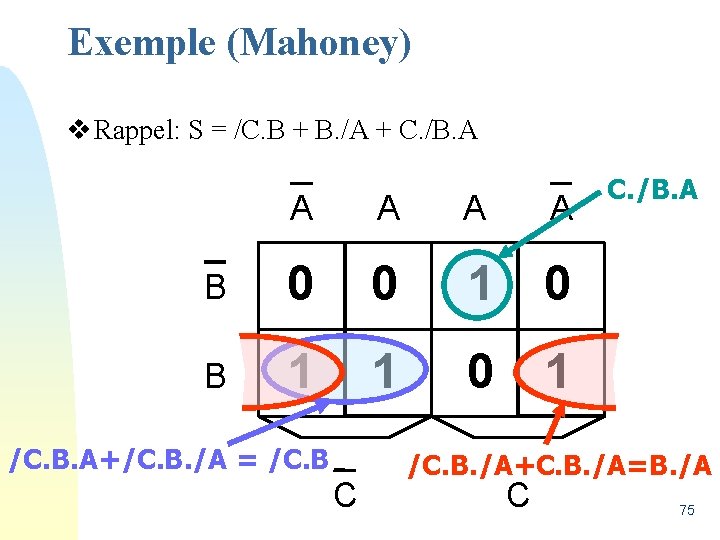
Exemple (Mahoney) TABLE DE VÉRITÉ A A B 0 0 1 0 B 1 1 0 1 C C TABLE DE MAHONEY 74

Exemple (Mahoney) v Rappel: S = /C. B + B. /A + C. /B. A A A B 0 0 1 0 B 1 1 0 1 /C. B. A+/C. B. /A = /C. B C C. /B. A /C. B. /A+C. B. /A=B. /A C 75

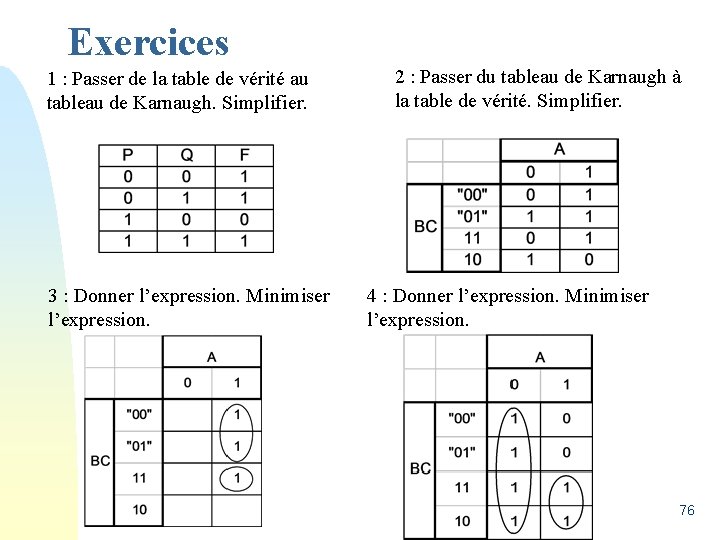
Exercices 1 : Passer de la table de vérité au tableau de Karnaugh. Simplifier. 3 : Donner l’expression. Minimiser l’expression. 2 : Passer du tableau de Karnaugh à la table de vérité. Simplifier. 4 : Donner l’expression. Minimiser l’expression. 76

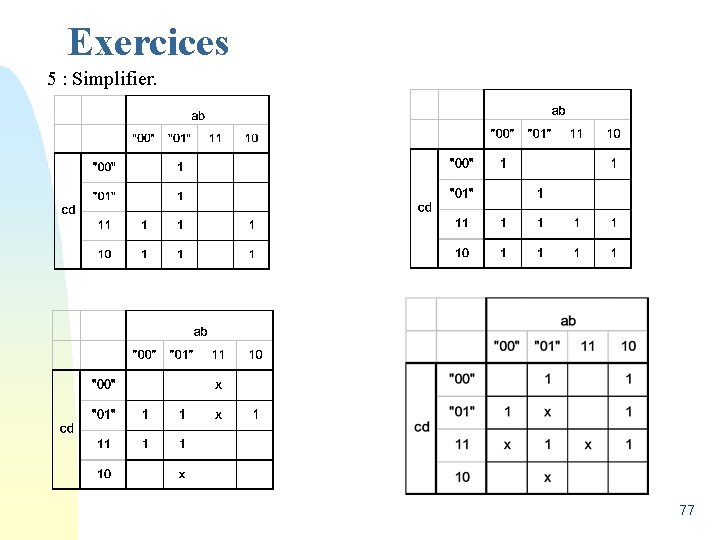
Exercices 5 : Simplifier. 77

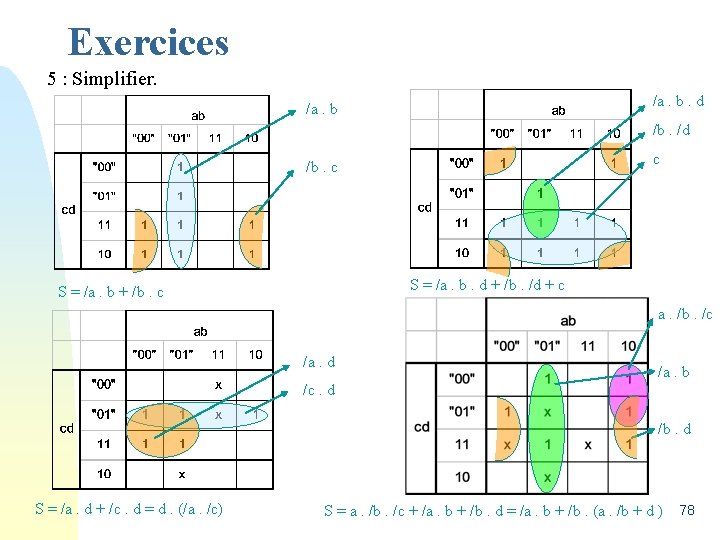
Exercices 5 : Simplifier. /a. b. d /a. b /b. /d c /b. c S = /a. b. d + /b. /d + c S = /a. b + /b. c a. /b. /c /a. d /a. b /c. d /b. d S = /a. d + /c. d = d. (/a. /c) S = a. /b. /c + /a. b + /b. d = /a. b + /b. (a. /b + d ) 78

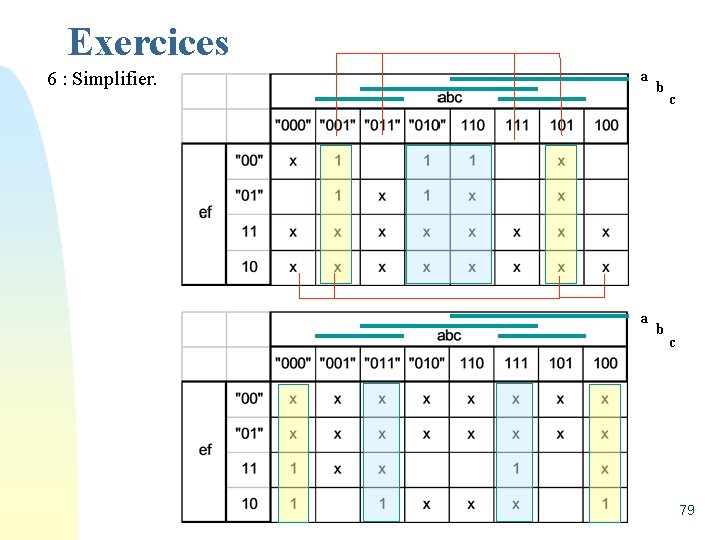
Exercices 6 : Simplifier. a a b b c c 79

Exercices 1 : Concevoir un circuit capable d’additionner deux bits, capable de générer leur somme S et leur report R. 2 : Concevoir un circuit de commande d’un afficheur 7 segments pour l’affichage des nombres 0, 1, 2, …, 9. (des états indifférents) e 3 : le poids le plus important e 0 : le poids le plus faible 80

Les états indifférents (don’t care) v Ils sont représentés par des X v En sortie, ils correspondent à des combinaisons d’entrées pour lesquelles la sortie n’a pas été définie. ¤ Ex. : Un réservoir ne peut être à la fois vide et plein. 81

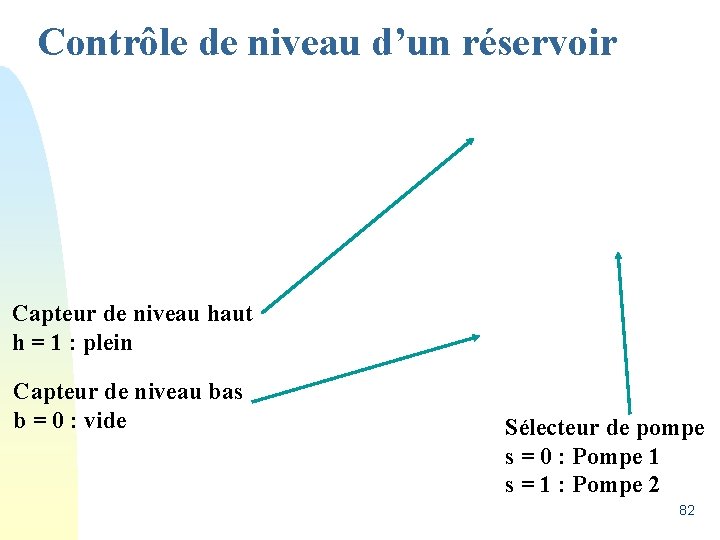
Contrôle de niveau d’un réservoir Capteur de niveau haut h = 1 : plein Capteur de niveau bas b = 0 : vide Sélecteur de pompe s = 0 : Pompe 1 s = 1 : Pompe 2 82

Contrôle de niveau. . . v Si réservoir plein: Aucune pompe en marche; v Si réservoir vide: Les 2 pompes en marche; v Si réservoir ni vide, ni plein: Faire fonctionner la pompe sélectionnée par le sélecteur « s » . 83

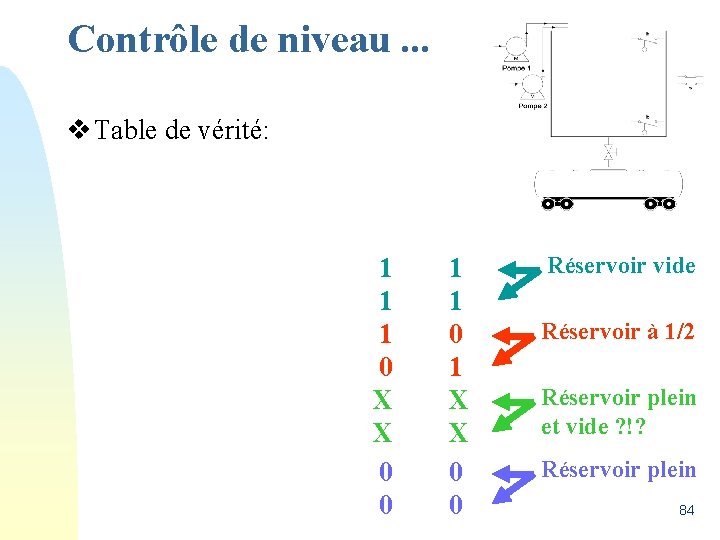
Contrôle de niveau. . . v Table de vérité: 1 1 1 0 X X 0 0 1 1 0 1 X X 0 0 Réservoir vide Réservoir à 1/2 Réservoir plein et vide ? !? Réservoir plein 84

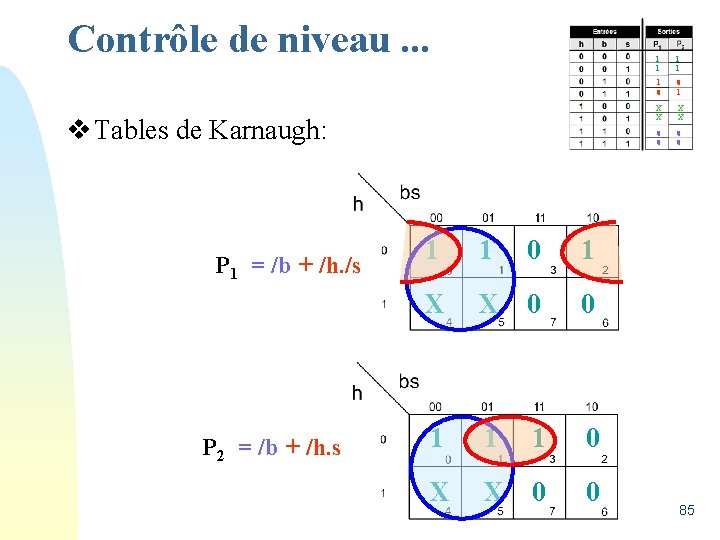
Contrôle de niveau. . . v Tables de Karnaugh: P 1 = /b + /h. /s P 2 = /b + /h. s 1 1 0 1 X X 0 0 1 1 1 0 0 1 X X 0 0 85

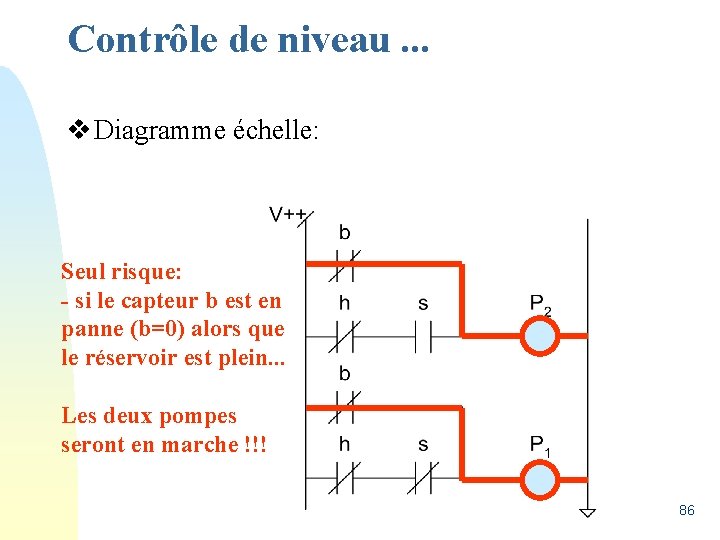
Contrôle de niveau. . . v Diagramme échelle: Seul risque: - si le capteur b est en panne (b=0) alors que le réservoir est plein. . . Les deux pompes seront en marche !!! 86

Contrôle de niveau. . . v Si on considère les X comme des 0. P 2 = /b. /h + /h. s P 1 = /b. /h + /h. /s 1 1 1 0 0 0 0 87

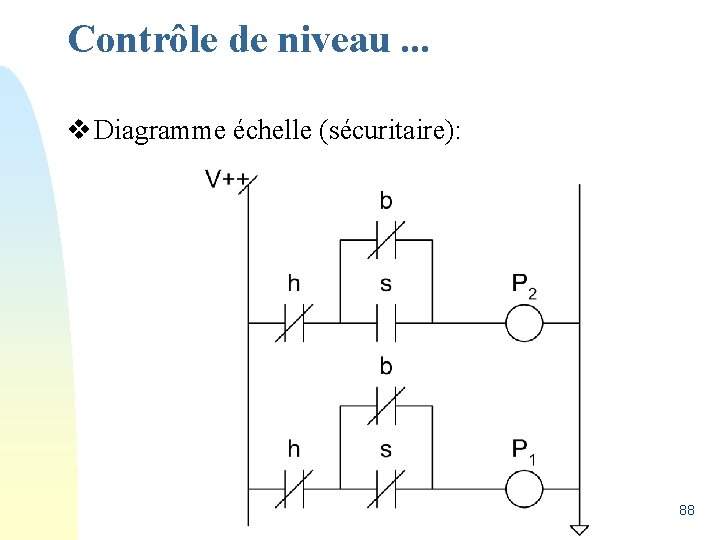
Contrôle de niveau. . . v Diagramme échelle (sécuritaire): 88

Conclusion de l’exemple v Les « X » peuvent êtres utilisés dans des groupes de 1 pour en augmenter la taille. ¤ Cela implique des équations plus simples; v Du point de vue sécurité, il peut s ’avérer nécessaire de considérer les « X » comme des « 0 » . 89

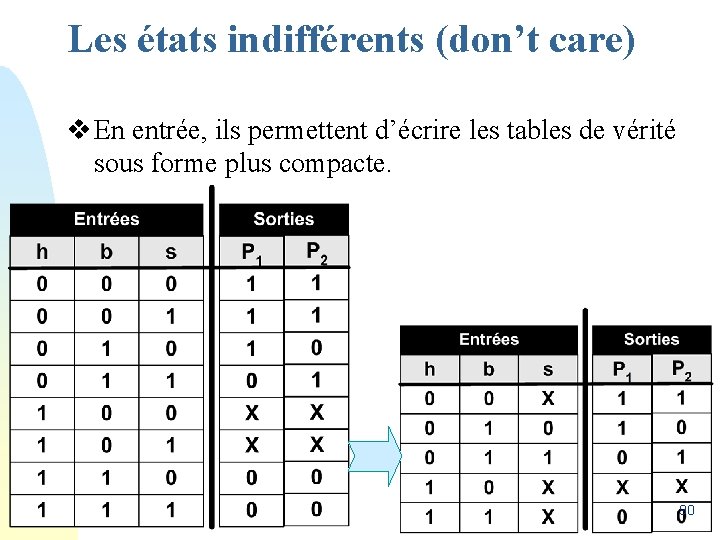
Les états indifférents (don’t care) v En entrée, ils permettent d’écrire les tables de vérité sous forme plus compacte. 90

Logique combinatoire v. s. Logique séquentielle Les premières méthodes d’automatisation pour les systèmes séquentiels. 91

La logique combinatoire et les automatismes v La logique combinatoire peut être utilisée pour étudier les automatismes simples. v L’exemple qui suit montre la marche à suivre. . . 92

Etapes de la démarche 1 Dénombrer tous les états possibles. Établir un diagramme des phases. Établir un diagramme des transitions. 2 Construire la table de vérité du système. 3 Trouver les équations logiques des actionneurs. 93

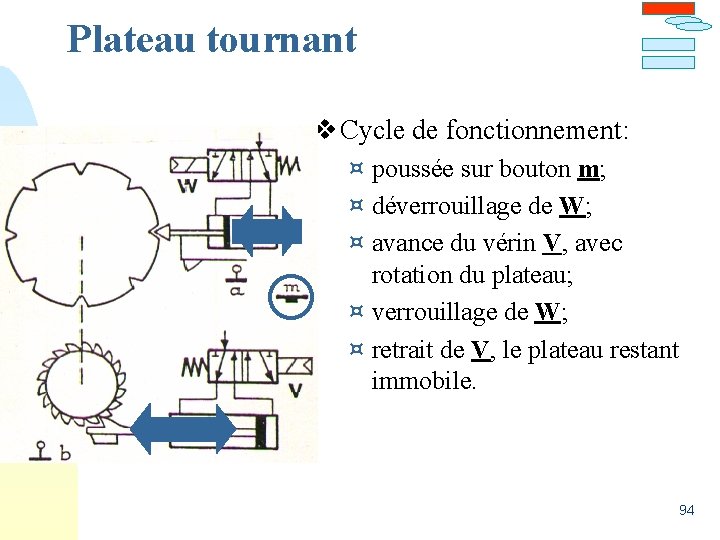
Plateau tournant v Cycle de fonctionnement: ¤ poussée sur bouton m; ¤ déverrouillage de W; ¤ avance du vérin V, avec rotation du plateau; ¤ verrouillage de W; ¤ retrait de V, le plateau restant immobile. 94

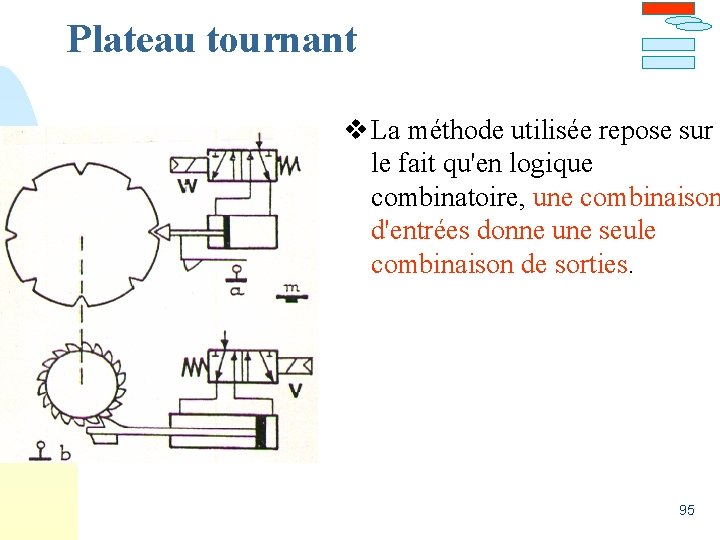
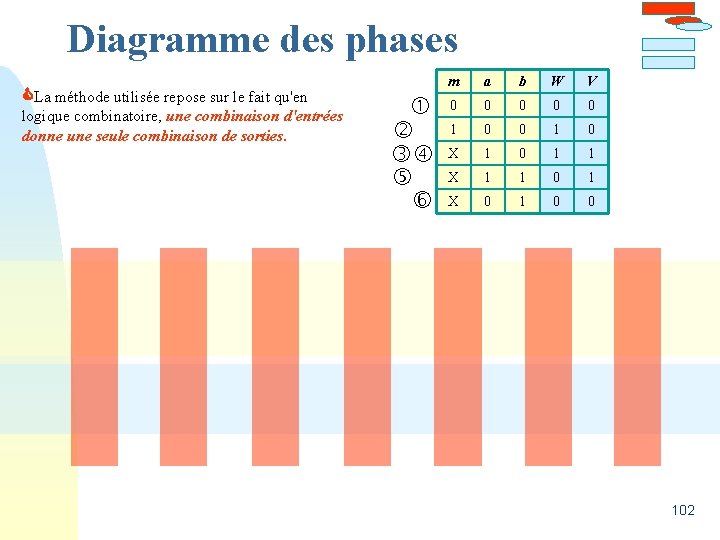
Plateau tournant v La méthode utilisée repose sur le fait qu'en logique combinatoire, une combinaison d'entrées donne une seule combinaison de sorties. 95

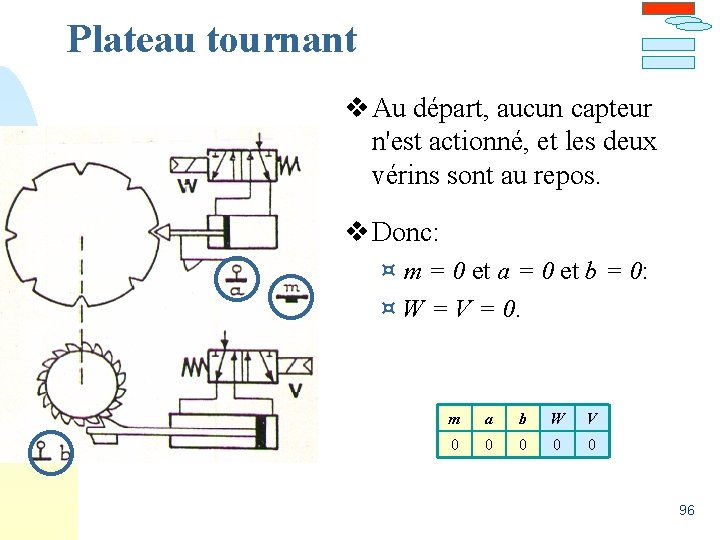
Plateau tournant v Au départ, aucun capteur n'est actionné, et les deux vérins sont au repos. v Donc: ¤ m = 0 et a = 0 et b = 0: ¤ W = V = 0. m a b W V 0 0 0 96

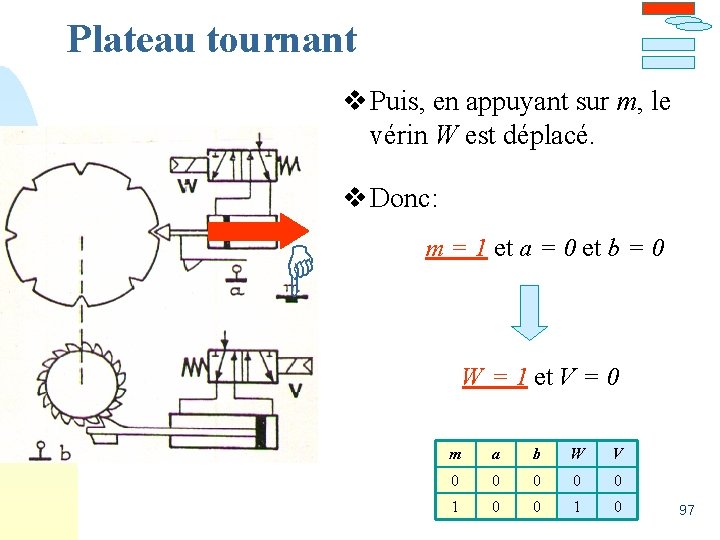
Plateau tournant v Puis, en appuyant sur m, le vérin W est déplacé. v Donc: m = 1 et a = 0 et b = 0 W = 1 et V = 0 m a b W V 0 0 0 1 0 97

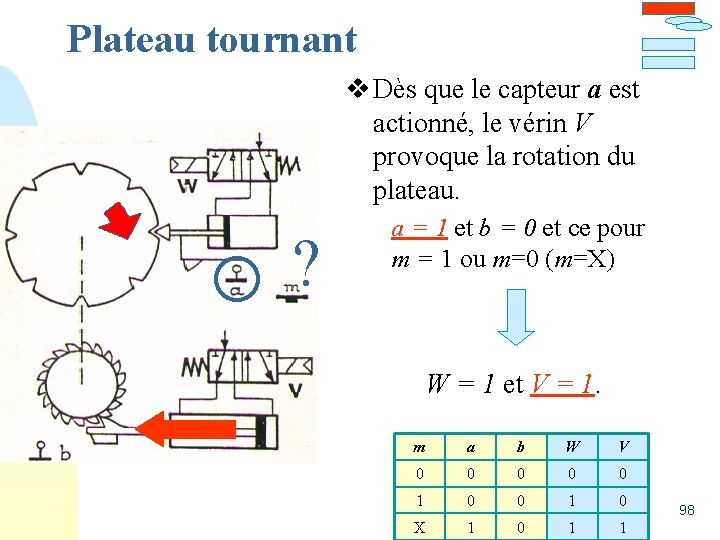
Plateau tournant v Dès que le capteur a est actionné, le vérin V provoque la rotation du plateau. ? a = 1 et b = 0 et ce pour m = 1 ou m=0 (m=X) W = 1 et V = 1. m a b W V 0 0 0 1 0 X 1 0 1 1 98

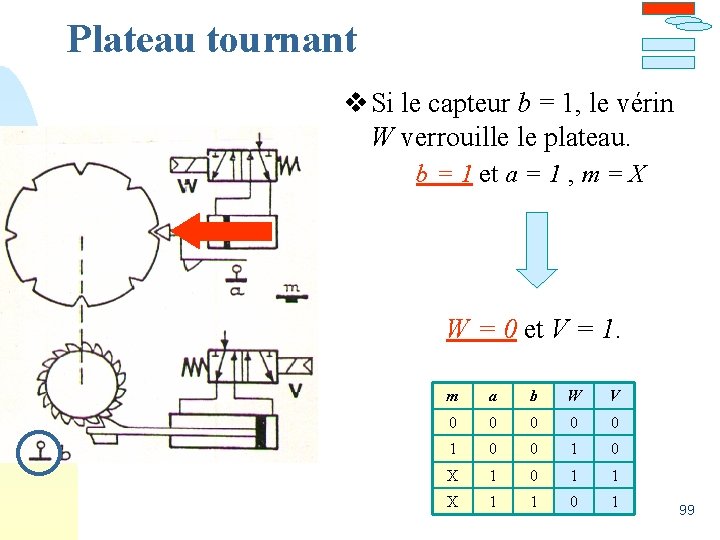
Plateau tournant v Si le capteur b = 1, le vérin W verrouille le plateau. b = 1 et a = 1 , m = X W = 0 et V = 1. m a b W V 0 0 0 1 0 X 1 0 1 1 X 1 1 0 1 99

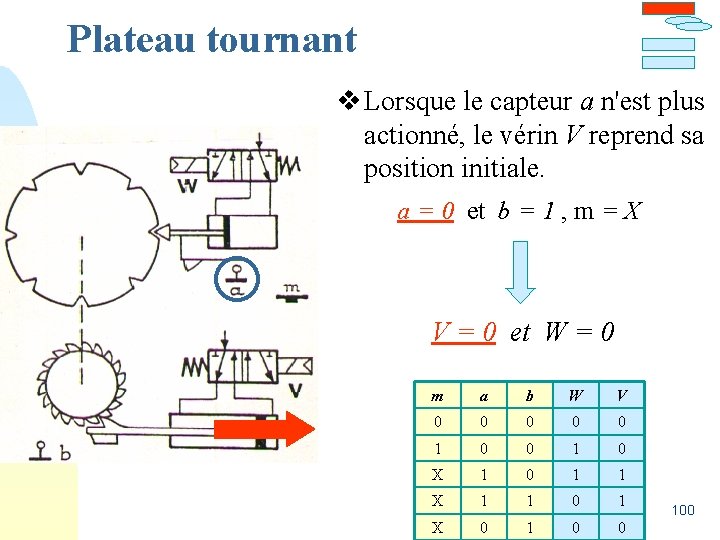
Plateau tournant v Lorsque le capteur a n'est plus actionné, le vérin V reprend sa position initiale. a = 0 et b = 1 , m = X V = 0 et W = 0 m a b W V 0 0 0 1 0 X 1 0 1 1 X 1 1 0 1 X 0 1 0 0 100

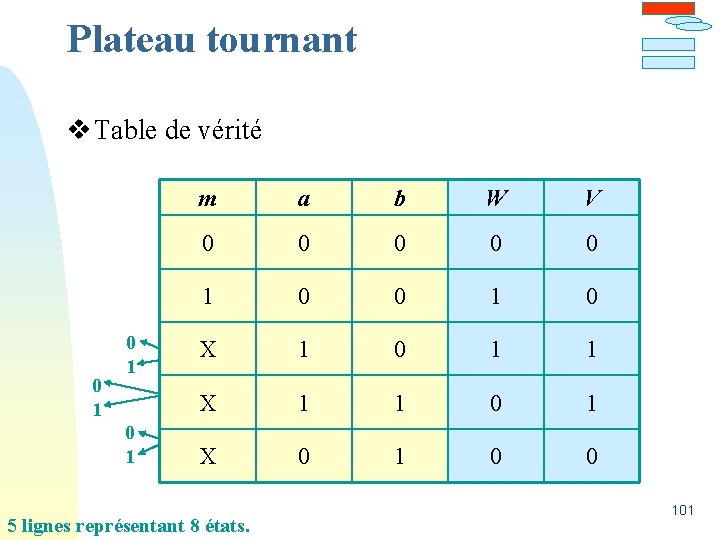
Plateau tournant v Table de vérité 0 1 0 1 m a b W V 0 0 0 1 0 X 1 0 1 1 X 1 1 0 1 X 0 1 0 0 5 lignes représentant 8 états. 101

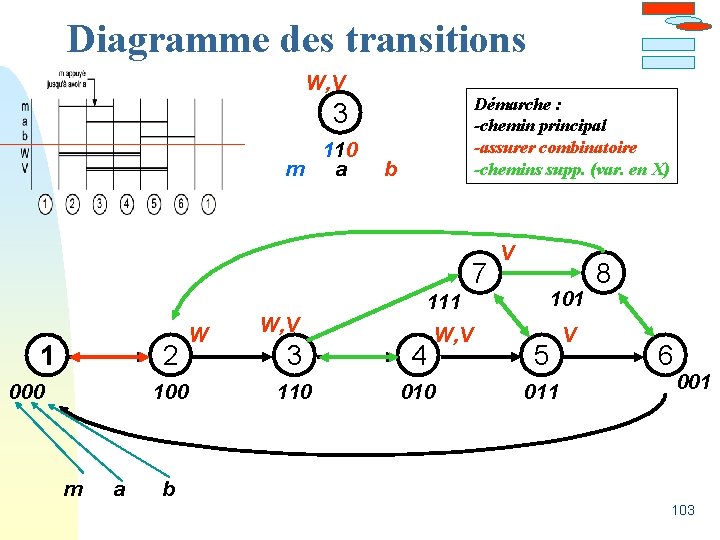
Diagramme des phases La méthode utilisée repose sur le fait qu'en logique combinatoire, une combinaison d'entrées donne une seule combinaison de sorties. m a b W V 0 0 0 1 0 X 1 0 1 1 X 1 1 0 1 X 0 1 0 0 102

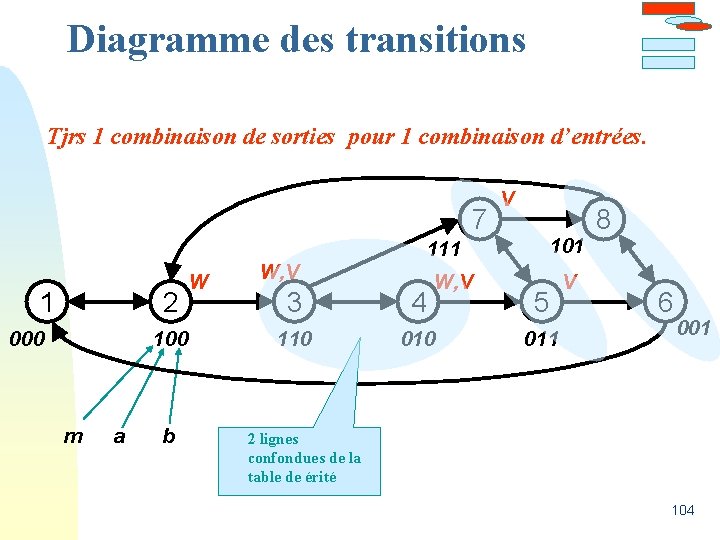
Diagramme des transitions W, V Démarche : -chemin principal -assurer combinatoire -chemins supp. (var. en X) 3 110 m a b 7 1 2 000 W 100 m a V 101 111 W, V 3 4 110 010 5 011 V 8 6 001 b 103

Diagramme des transitions Tjrs 1 combinaison de sorties pour 1 combinaison d’entrées. 7 1 2 000 W 100 m a b V 101 111 W, V 3 4 110 010 5 011 V 8 6 001 2 lignes confondues de la table de érité 104

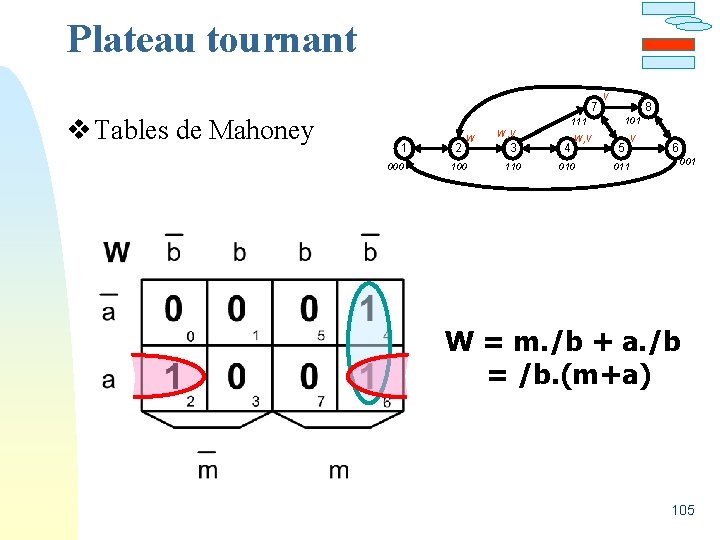
Plateau tournant v Tables de Mahoney 7 V 8 101 111 1 000 2 W 100 W, V 3 4 110 010 5 V 011 6 001 W = m. /b + a. /b = /b. (m+a) 105

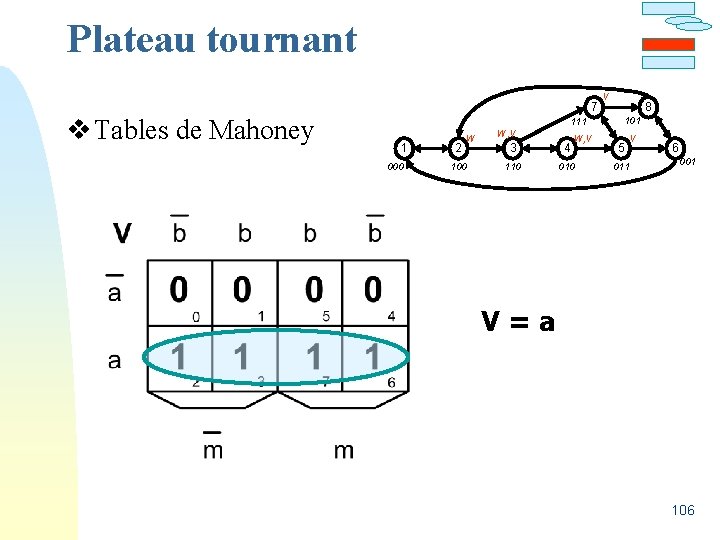
Plateau tournant v Tables de Mahoney 7 V 8 101 111 1 000 2 W 100 W, V 3 4 110 010 5 V 011 6 001 V=a 106

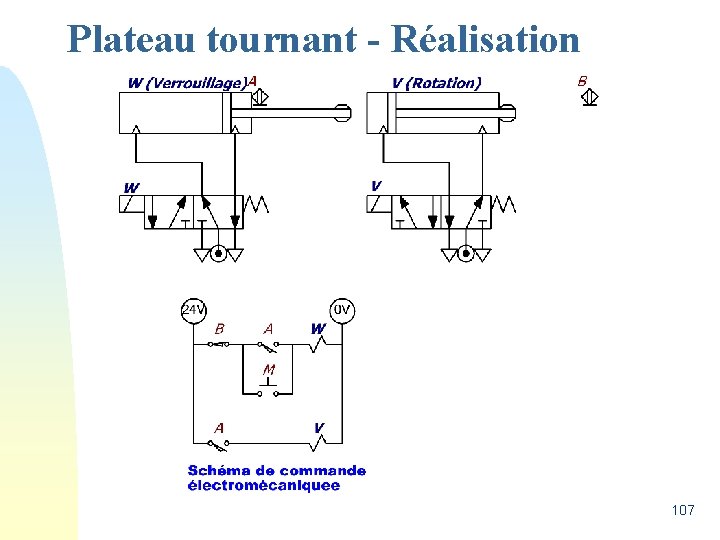
Plateau tournant - Réalisation 107

Méthode de Huffman Exemple où la résolution combinatoire devient impossible. Marche (m) et Arrêt (a) d ’un Moteur (C) : Mise en Marche : Si (a = 0 ET m = 1 ) Alors (C = 1) Moteur en marche : Si (a = 0 ET m = 0 ) Alors (C = 1) Mise à l’arrêt : Si (a = 1 ET m = 0) Alors (C = 0) Arret : Si (a = 0 ET m = 0 ) Alors (C = 0) Huffman 108

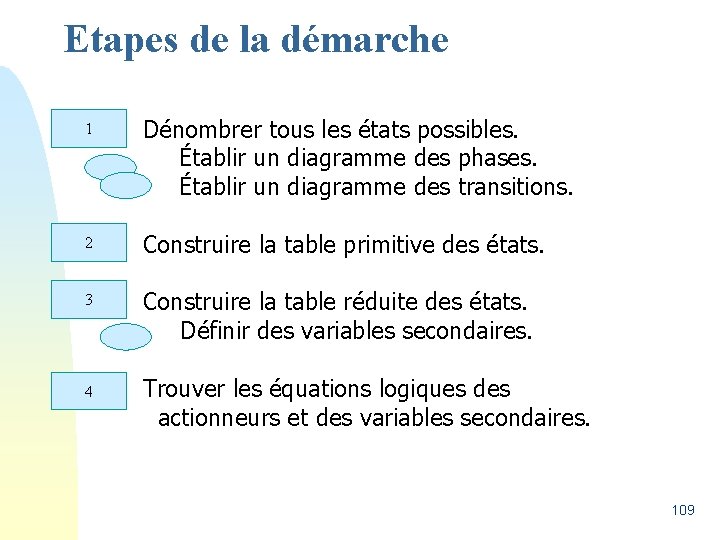
Etapes de la démarche 1 Dénombrer tous les états possibles. Établir un diagramme des phases. Établir un diagramme des transitions. 2 Construire la table primitive des états. 3 Construire la table réduite des états. Définir des variables secondaires. 4 Trouver les équations logiques des actionneurs et des variables secondaires. 109

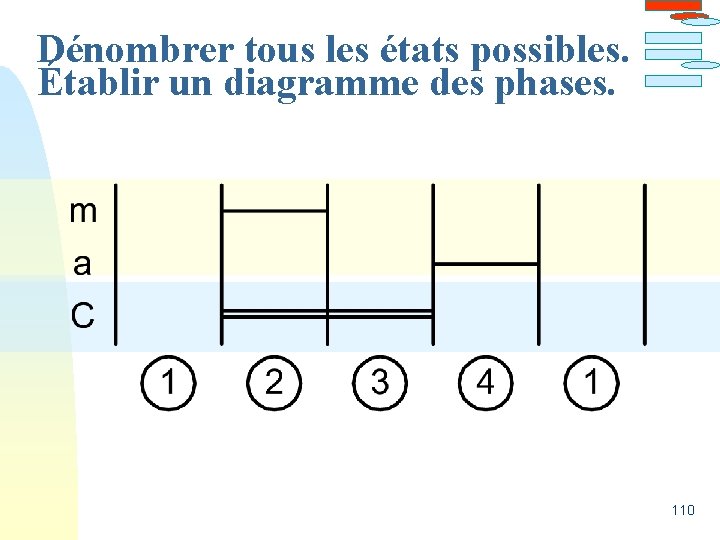
Dénombrer tous les états possibles. Établir un diagramme des phases. 110

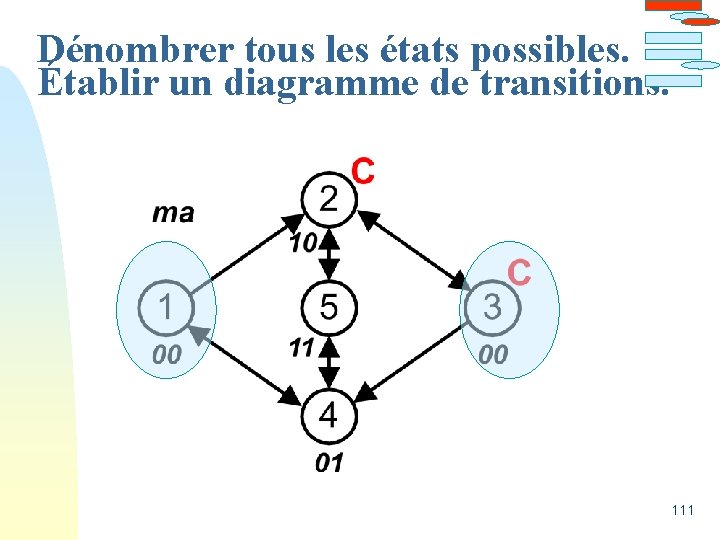
Dénombrer tous les états possibles. Établir un diagramme de transitions. 111

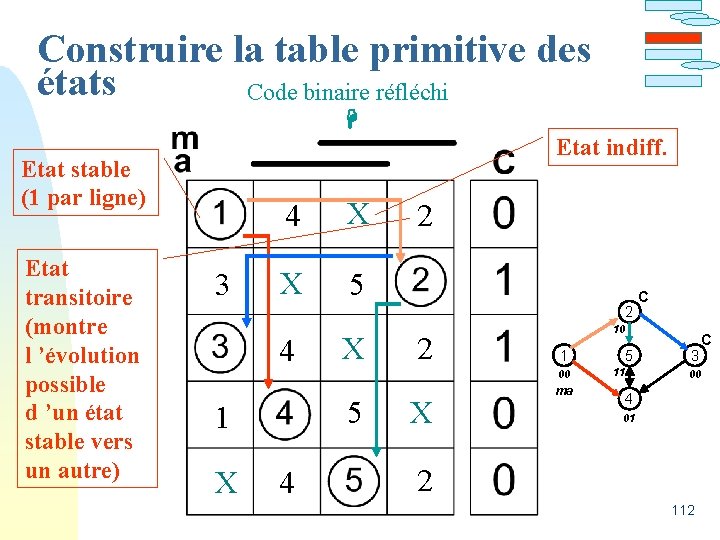
Construire la table primitive des états Code binaire réfléchi Etat indiff. Etat stable (1 par ligne) Etat transitoire (montre l ’évolution possible d ’un état stable vers un autre) 3 4 X X 5 2 2 4 X 2 10 1 00 5 1 X 4 X C ma 5 11 3 C 00 4 01 2 112

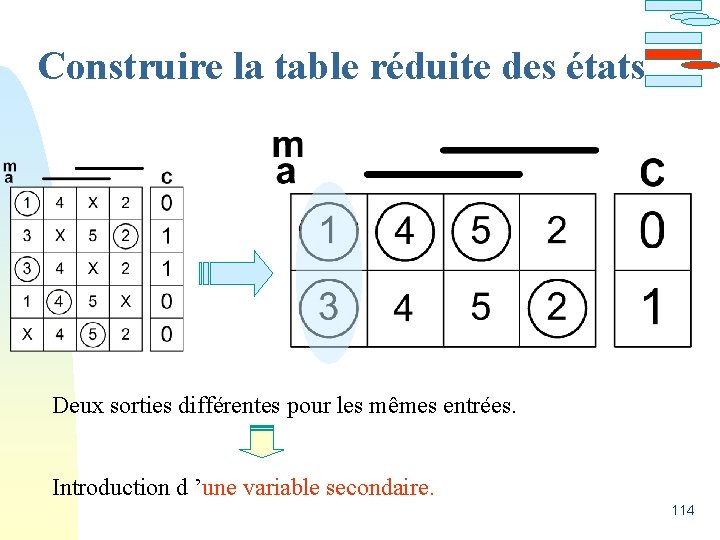
Construire la table réduite des états Le regroupement de lignes de la matrice primitive doit obéir aux règles suivantes : ·Les niveaux logiques de la ou des sorties doivent être les mêmes sur les lignes à regrouper. ·Les états sur chacune des lignes à regrouper doivent être les mêmes ou correspondre à un X. . Les états sont fusionnés selon la règle : > 3 > X 113

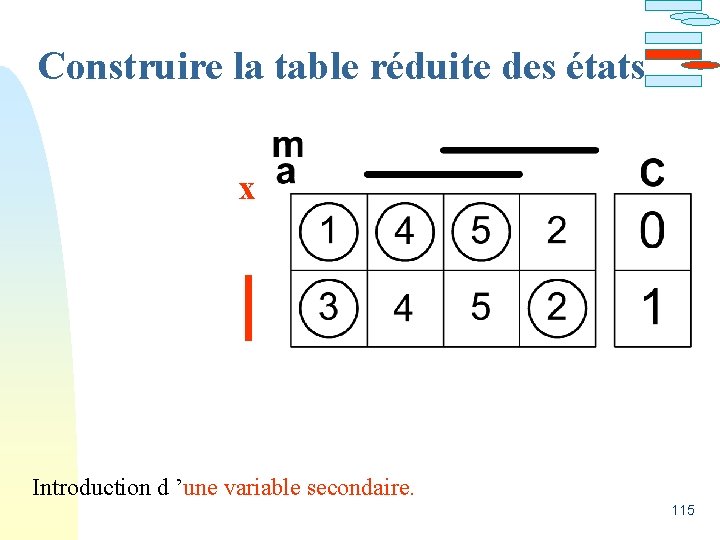
Construire la table réduite des états Deux sorties différentes pour les mêmes entrées. Introduction d ’une variable secondaire. 114

Construire la table réduite des états x Introduction d ’une variable secondaire. 115

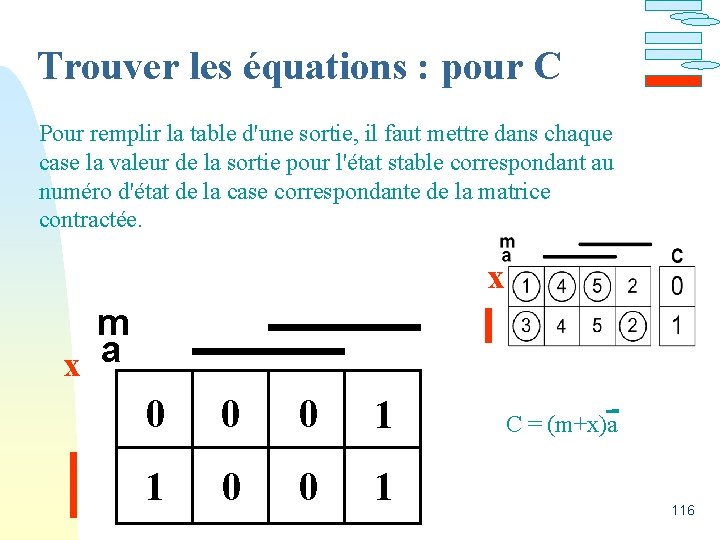
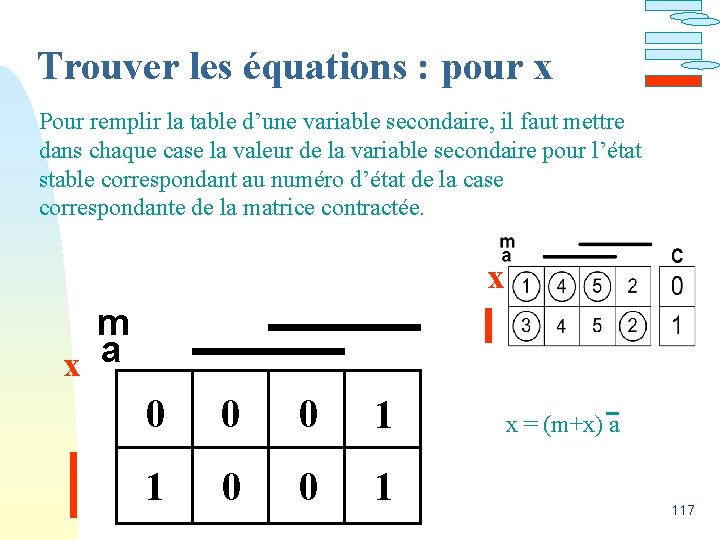
Trouver les équations : pour C Pour remplir la table d'une sortie, il faut mettre dans chaque case la valeur de la sortie pour l'état stable correspondant au numéro d'état de la case correspondante de la matrice contractée. x m x a 0 0 0 1 1 0 0 1 C = (m+x)a 116

Trouver les équations : pour x Pour remplir la table d’une variable secondaire, il faut mettre dans chaque case la valeur de la variable secondaire pour l’état stable correspondant au numéro d’état de la case correspondante de la matrice contractée. x m x a 0 0 0 1 1 0 0 1 x = (m+x) a 117

Exercice : Plateau tournant (huffmann) Aucune contrainte pour l’opérateur. 118

Méthodes intuitives (fondées sur la méthode de Huffman) Dans certains automatismes les variables secondaires sont les sorties du système. 119

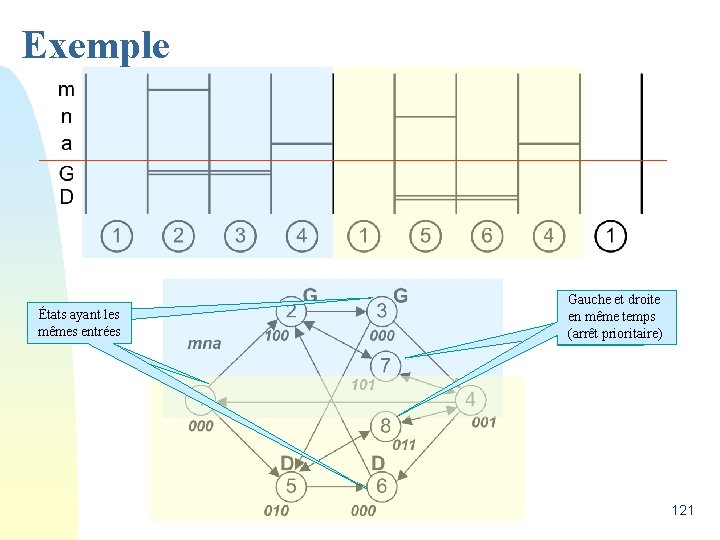
Exemple • Un moteur qui peut tourner vers la gauche (contacteur « G » ) ou vers la droite (contacteur « D » ). Ce moteur est commandé par trois boutons : • « m » et « n » qui sont verrouillés mécaniquement (donc impossibles à actionner en même temps) et qui correspondent respectivement à une rotation à gauche et une rotation à droite; • « a » qui est le bouton d’arrêt (prioritaire si appuyé en même temps que « m » et « n » ). 120

Exemple États ayant les mêmes entrées Gauche et droite en même temps (arrêt prioritaire) 121

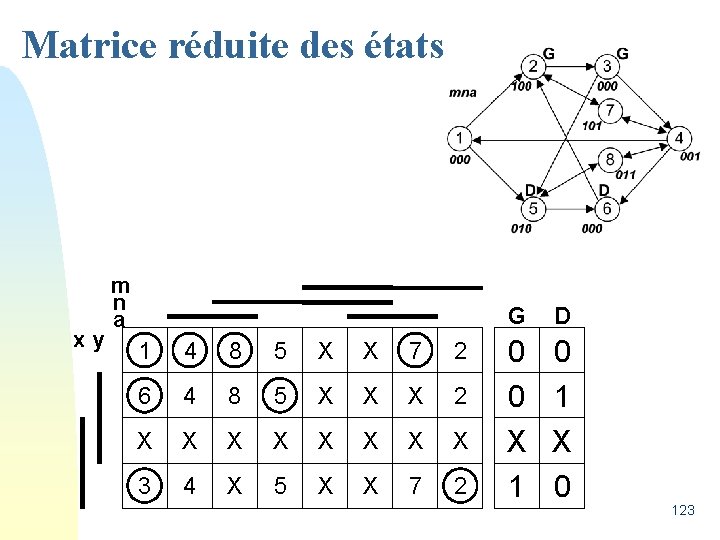
Exemple Il faut deux variables intermédiaires pour distinguer ces trois états. Ils se différencient grâce à leur sortie. Les Sorties seront les variables intermédiaires. Choisissons : x=G et y=D 122

Matrice réduite des états xy m n a G D 1 4 8 5 X X 7 2 0 0 6 4 8 5 X X X 2 0 1 X X X X X 3 4 X 5 X X 7 2 1 0 123

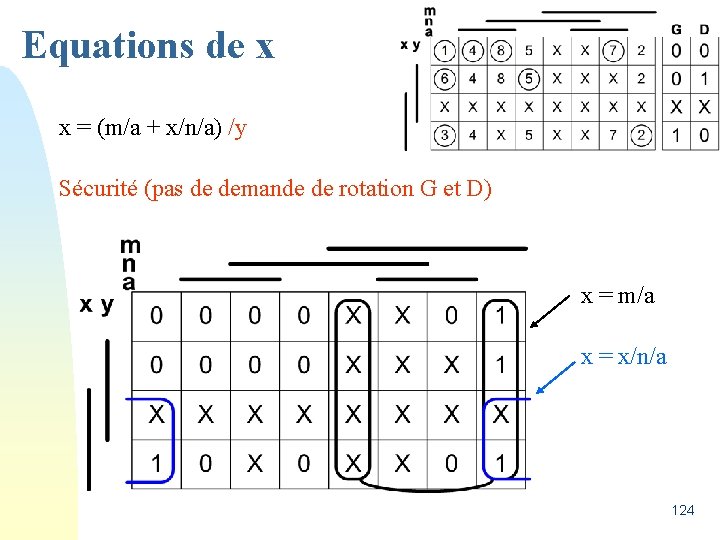
Equations de x x = (m/a + x/n/a) /y Sécurité (pas de demande de rotation G et D) x = m/a x = x/n/a 124

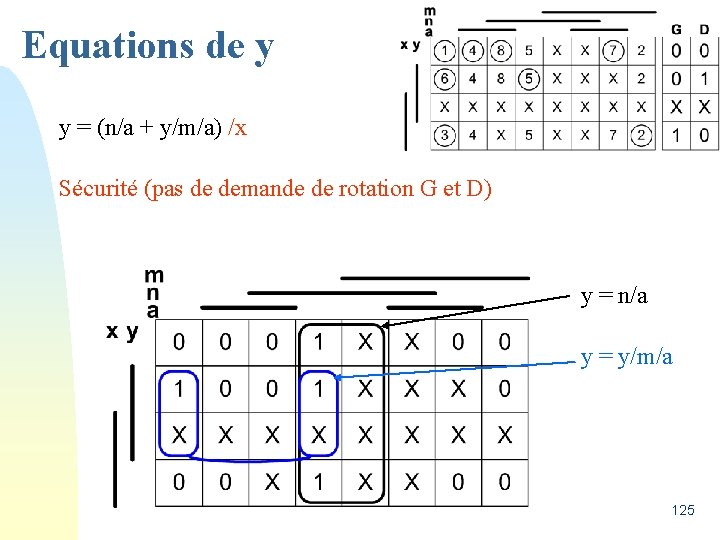
Equations de y y = (n/a + y/m/a) /x Sécurité (pas de demande de rotation G et D) y = n/a y = y/m/a 125

Étude simplifiée des automatismes à cycles géométriques 126

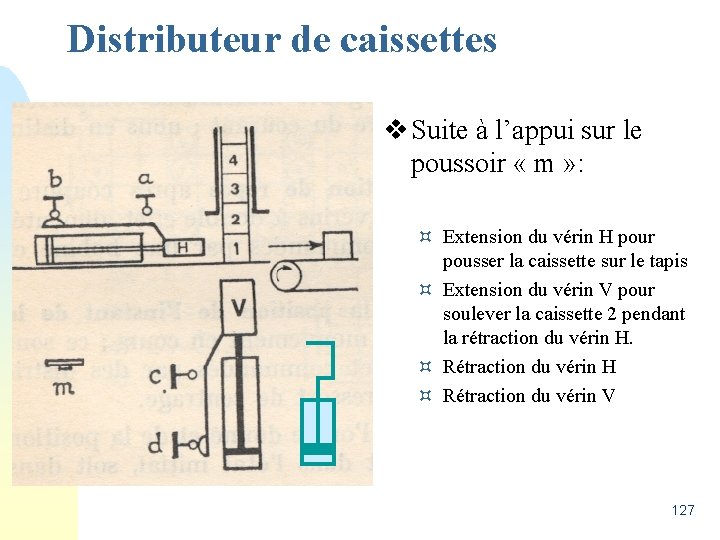
Distributeur de caissettes v Suite à l’appui sur le poussoir « m » : ¤ Extension du vérin H pour pousser la caissette sur le tapis ¤ Extension du vérin V pour soulever la caissette 2 pendant la rétraction du vérin H. ¤ Rétraction du vérin H ¤ Rétraction du vérin V 127

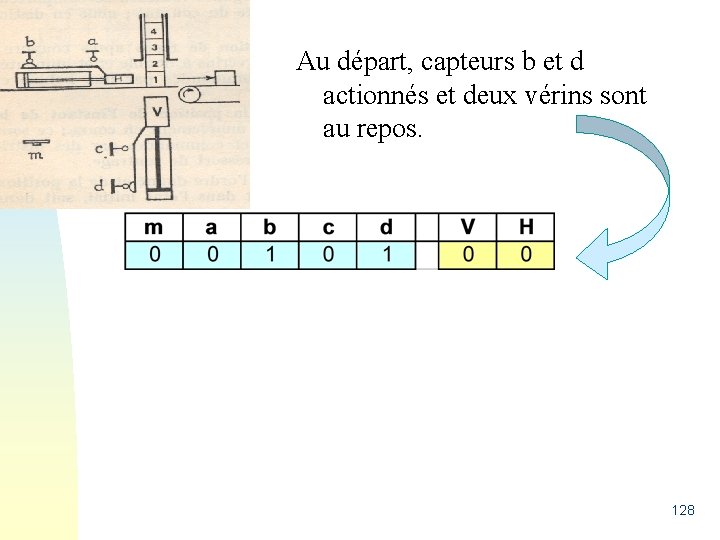
Au départ, capteurs b et d actionnés et deux vérins sont au repos. 128

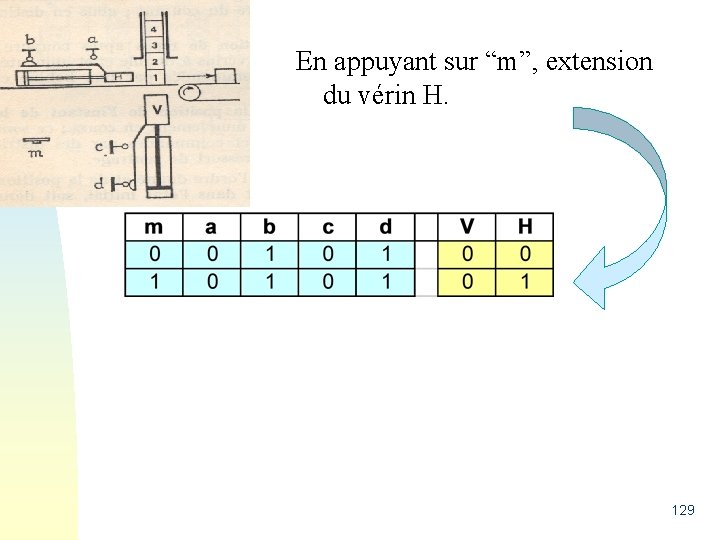
En appuyant sur “m”, extension du vérin H. 129

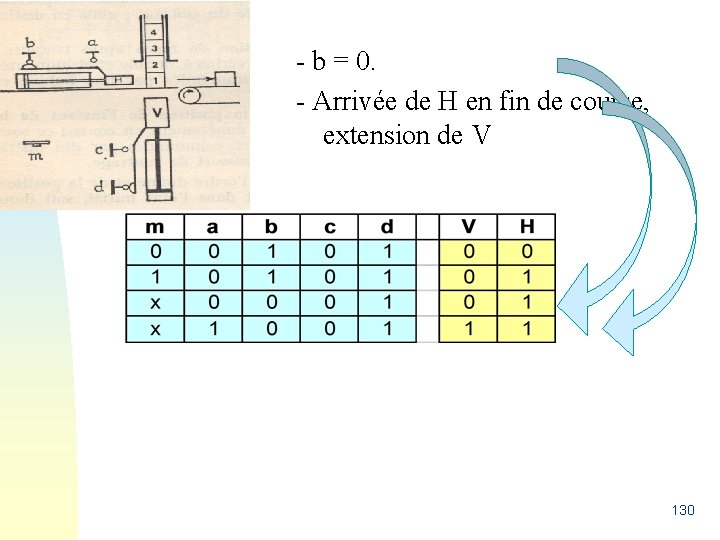
- b = 0. - Arrivée de H en fin de course, extension de V 130

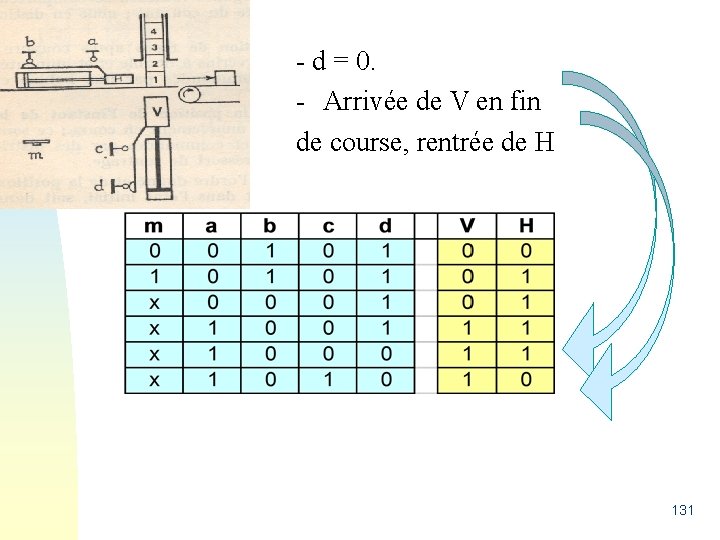
- d = 0. - Arrivée de V en fin de course, rentrée de H 131

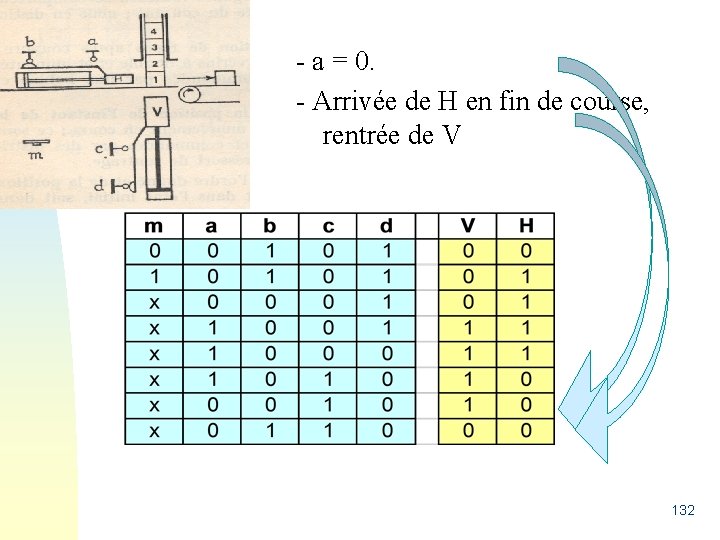
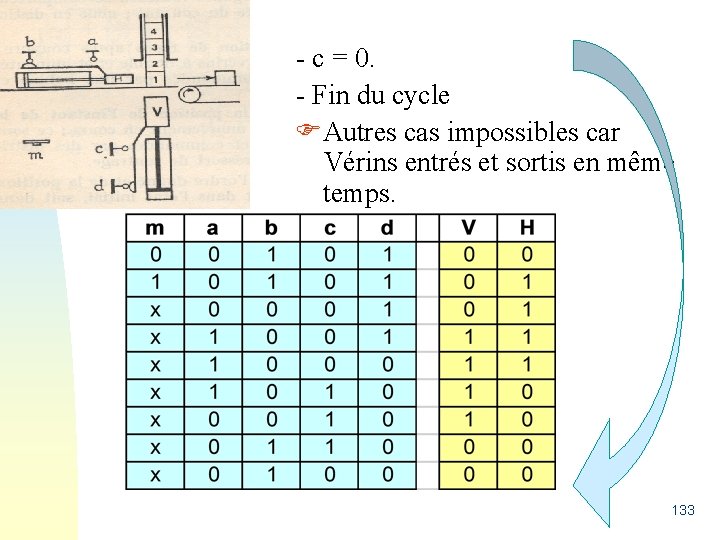
- a = 0. - Arrivée de H en fin de course, rentrée de V 132

- c = 0. - Fin du cycle Autres cas impossibles car Vérins entrés et sortis en même temps. 133

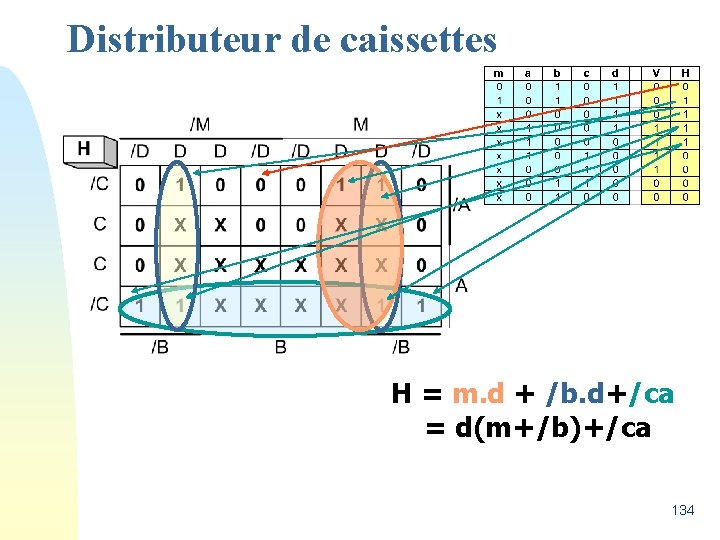
Distributeur de caissettes H = m. d + /b. d+/ca = d(m+/b)+/ca 134

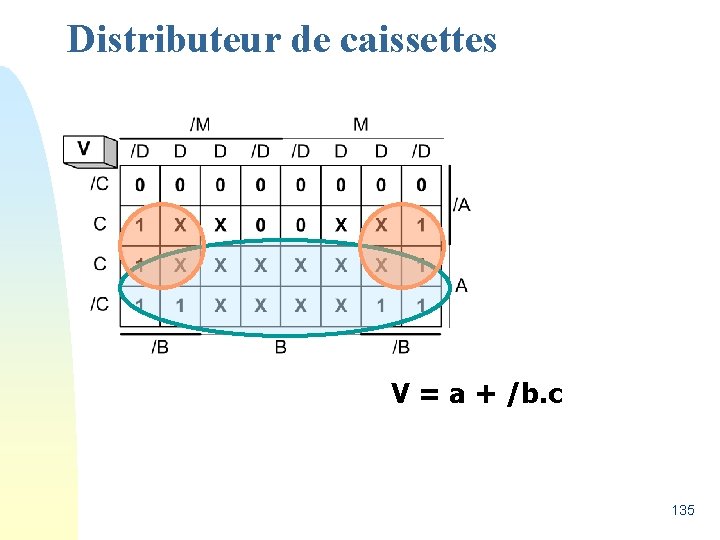
Distributeur de caissettes V = a + /b. c 135

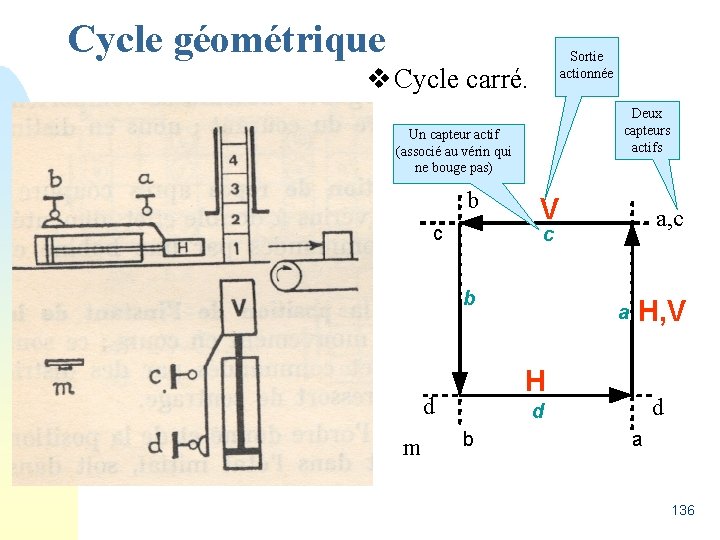
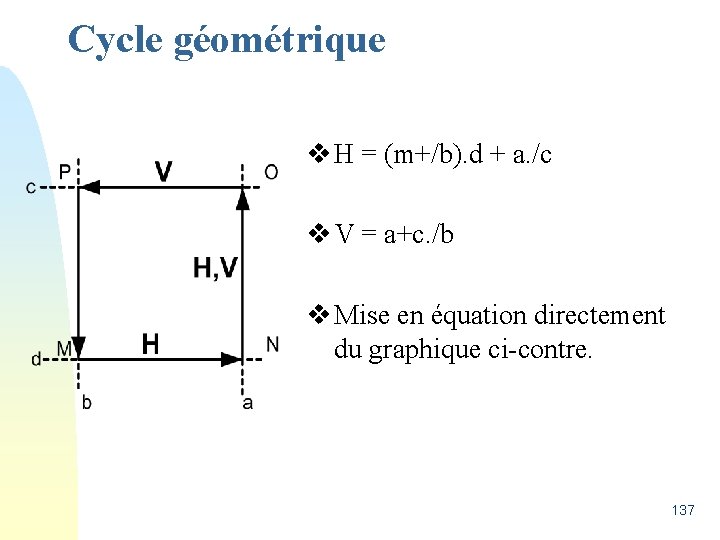
Cycle géométrique Sortie actionnée v Cycle carré. Deux capteurs actifs Un capteur actif (associé au vérin qui ne bouge pas) b c V c b a H, V H d m a, c d d b a 136

Cycle géométrique v H = (m+/b). d + a. /c v V = a+c. /b v Mise en équation directement du graphique ci-contre. 137

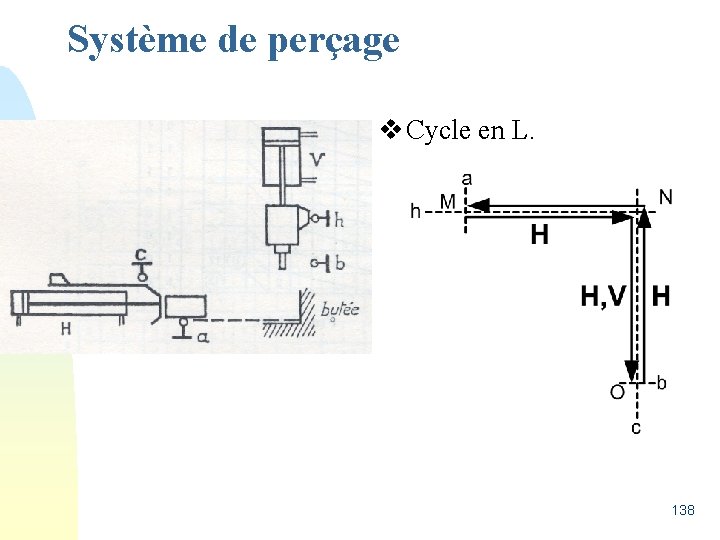
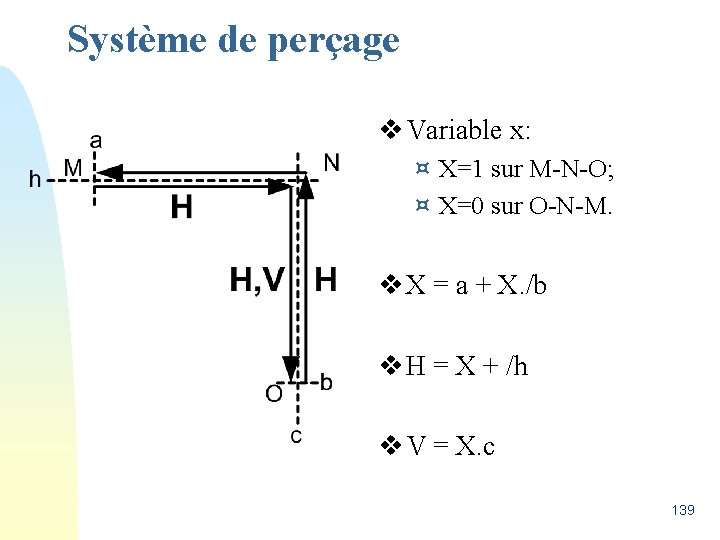
Système de perçage v Cycle en L. 138

Système de perçage v Variable x: ¤ X=1 sur M-N-O; ¤ X=0 sur O-N-M. v X = a + X. /b v H = X + /h v V = X. c 139

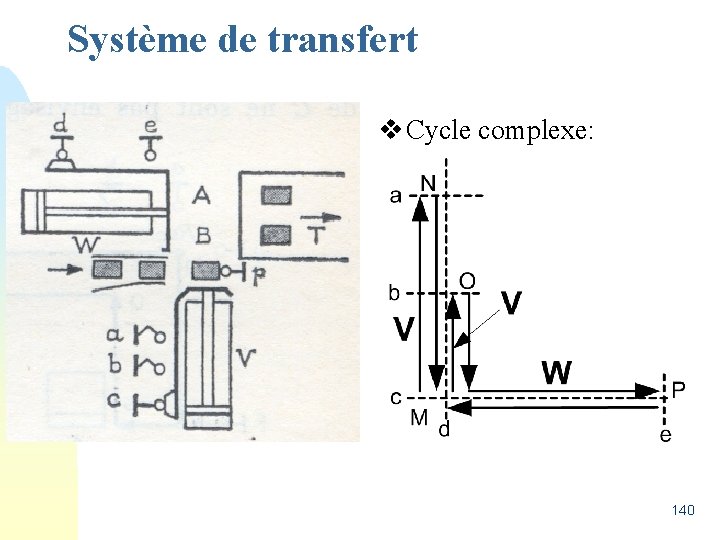
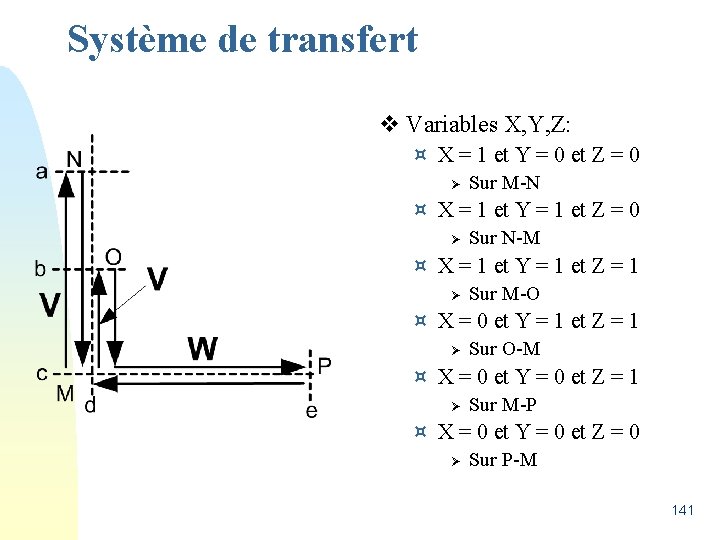
Système de transfert v Cycle complexe: 140

Système de transfert v Variables X, Y, Z: ¤ X = 1 et Y = 0 et Z = 0 Ø Sur M-N ¤ X = 1 et Y = 1 et Z = 0 Ø Sur N-M ¤ X = 1 et Y = 1 et Z = 1 Ø Sur M-O ¤ X = 0 et Y = 1 et Z = 1 Ø Sur O-M ¤ X = 0 et Y = 0 et Z = 1 Ø Sur M-P ¤ X = 0 et Y = 0 et Z = 0 Ø Sur P-M 141

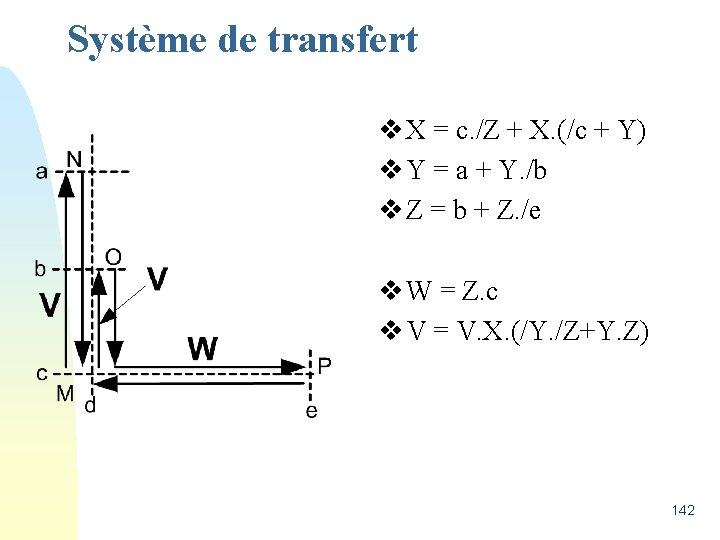
Système de transfert v X = c. /Z + X. (/c + Y) v Y = a + Y. /b v Z = b + Z. /e v W = Z. c v V = V. X. (/Y. /Z+Y. Z) 142

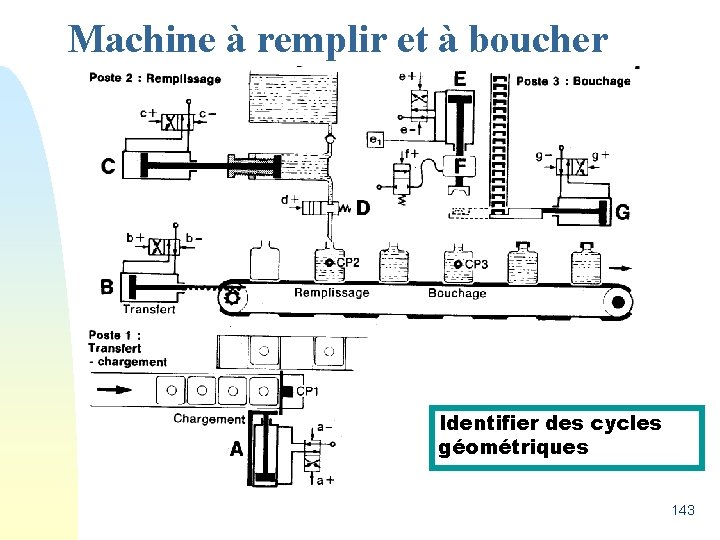
Machine à remplir et à boucher Identifier des cycles géométriques 143