Logique du premier ordre Logique de prdicats Chap

Logique du premier ordre (Logique de prédicats) Chap. 8 1

Plan • Pourquoi utiliser la logique du premier ordre (LPO)? • Syntaxe et sémantique • Utiliser la LPO • Le monde de Wumpus en LPO • Engenierie de connaissances dans LPO 2

Logique propositionnelle: pours et contres Logique propositionnelle est déclarative Logique propositionnelle permet d’exprimer des informations partielles/disjonctives/négatives – (contraste avec la plupart des structures de données et les bases de données) Logique propositionnelle est compositionnelle: – Le sens du tout est composé des sens des parties – Sens de B 1, 1 P 1, 2 est dérivé du sens de B 1, 1 et de P 1, 2 Sens dans logique propositionnelle est hors-contexte (context -independent) – (différent de la langue naturelle où le sens est dépendant du contexte) Logique propositionnelle est limitée en capacité d’expression – (pas comme en langue naturelle) – E. g. , ne peut pas exprimer ”les fosses causent la brise dans les carrés adjacents” • À moins d’écrire une phrase par carré 3

Logique du premier ordre • Logique propositionnelle suppose que le monde contient des faits, • Logique du premier ordre suppose que le monde contient: – Objets (D): personnes, maisons, nombres, couleurs, match de baseball, guerre, … variable – Relations (Dn {vrai, faux}): rouge, rond, nombre-premier, est frère de, est plus grand que, est partie de, … – Fonctions (Dn D): père de, meilleur ami de, un de plus que, … 4

Fonction vs. prédicat Jean Marie Philippe • Fonction: père_de(Philippe) = Jean • Prédicat: est_père_de(Jean, Philippe) = vrai • Les noms importent peu. C’est la définition qui est importante. 5

Syntaxe de LPO: éléments de base • • Constantes (Objets): King. John, 2, Ude. M, . . . Prédicats: Brother, >, . . . Fonctions: Sqrt, Left. Leg. Of, . . . Variables: x, y, a, b, . . . (minuscule) Connecteurs: , , Égalité: = Quantificateurs: , 6

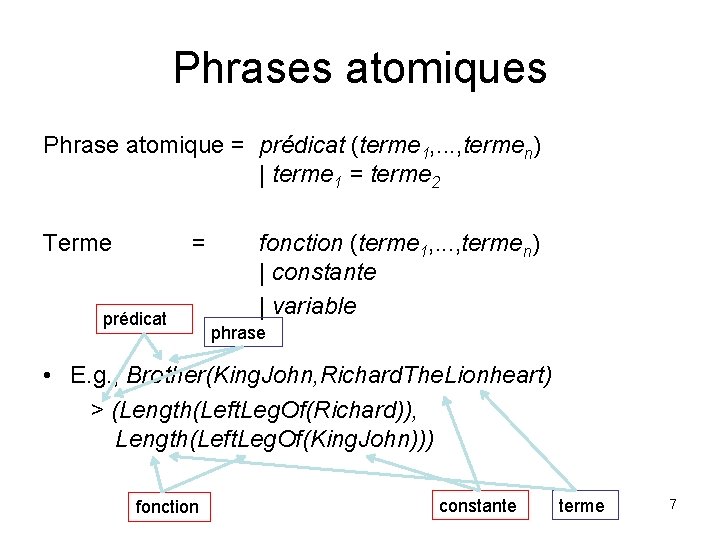
Phrases atomiques Phrase atomique = prédicat (terme 1, . . . , termen) | terme 1 = terme 2 Terme = prédicat fonction (terme 1, . . . , termen) | constante | variable phrase • E. g. , Brother(King. John, Richard. The. Lionheart) > (Length(Left. Leg. Of(Richard)), Length(Left. Leg. Of(King. John))) fonction constante terme 7

Phrases complexes • Les phrases complexes sont composées des phrases atomiques avec des connecteurs S, S 1 S 2, E. g. Sibling(King. John, Richard) Sibling(Richard, King. John) >(1, 2) ≤ (1, 2) >(1, 2) 8

Valeur de vérité en LPO • Les phrases sont vraies par rapport à un modèle et à une interprétation • Un modèle contient des objets (éléments du domaine) et des relations entre eux • Une interprétation spécifie les référés pour Symboles de constante → objets (la personne John) symboles de prédicat → relations (relation de père-fils) symboles de fonction → relation fonctionnelle (père-de) • Une phrase atomique prédicat(terme 1, . . . , termen) est vraie ssi les objets référés par terme 1, . . . , termen sont en relation référée par prédicat 9

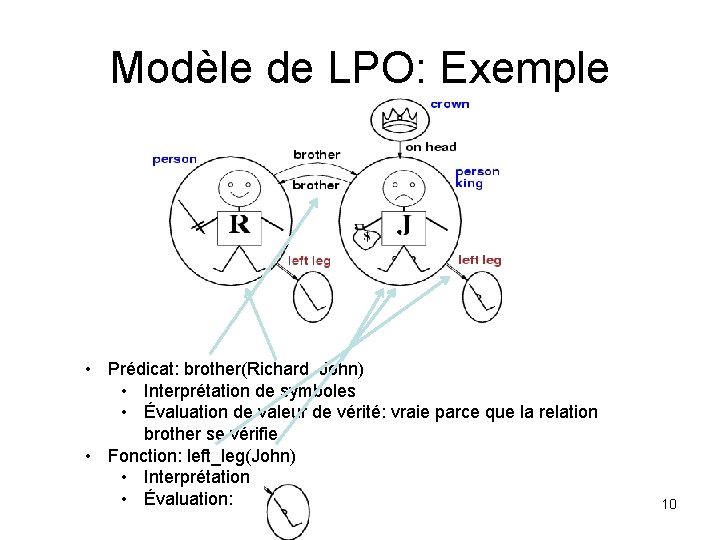
Modèle de LPO: Exemple • Prédicat: brother(Richard, John) • Interprétation de symboles • Évaluation de valeur de vérité: vraie parce que la relation brother se vérifie • Fonction: left_leg(John) • Interprétation • Évaluation: 10

Quantificateur Universel • <variables> <phrase> Everyone at Ude. M is smart (Tout le monde dans Ude. M est intelligent): x At(x, Ude. M) Smart(x) • x P est vraie dans un modèle m ssi P est vraie avec chaque objet qu’on peut assigner à x dans son domaine • Grosso modo: équivalent à la conjonction des instantiations de P . . . At(King. John, Ude. M) Smart(King. John) At(Richard, Ude. M) Smart(Richard) At(Ude. M, Ude. M) Smart(Ude. M) 11

Une erreur commune à éviter • typiquement, est le connecteur principal avec • Erreur commune: utiliser comme connecteur principal avec : – Correct Tout le monde dans Ude. M est intelligent: x At(x, Ude. M) Smart(x) – Incorrect x At(x, Ude. M) Smart(x) signifie “Everyone is at Ude. M and everyone is smart”(tout le monde est à Ude. M et tout le monde est intelligent) 12

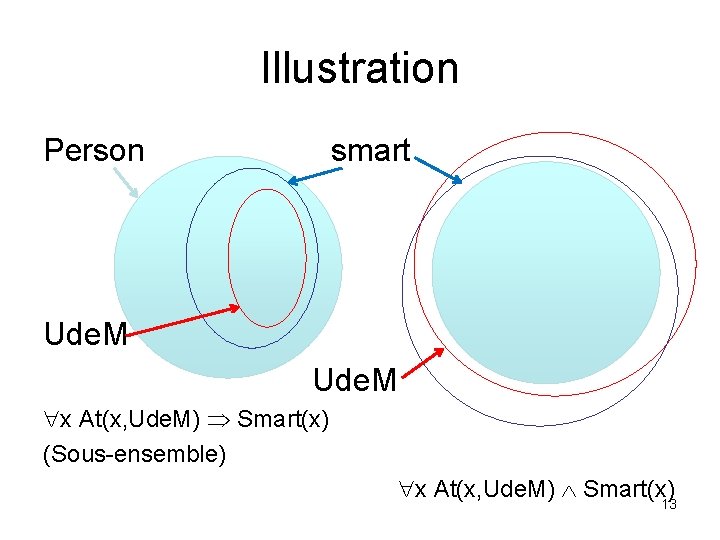
Illustration Person smart Ude. M x At(x, Ude. M) Smart(x) (Sous-ensemble) x At(x, Ude. M) Smart(x) 13

Quantification existentielle • <variables> <phrase> • Someone at Ude. M is smart (Quelqu’un à Ude. M est intelligent): – x At(x, Ude. M) Smart(x) • x P est vraie dans un modèle m ssi P est vraie avec x associée à un certain objet possible dans le modèle • Grosso modo: équivalent à la disjonction d’instanciations de P At(King. John, Ude. M) Smart(King. John) At(Richard, Ude. M) Smart(Richard) At(Ude. M, Ude. M) Smart(Ude. M) . . . 14

Une autre erreur commune à éviter • Typiquement, est généralement utilisé avec • Erreur commune: utiliser comme le connecteur principal avec : – Correct x At(x, Ude. M) Smart(x) – Incorrect x At(x, Ude. M) Smart(x) est vraie s’il existe quelqu’un qui n’est pas à Ude. M ! 15

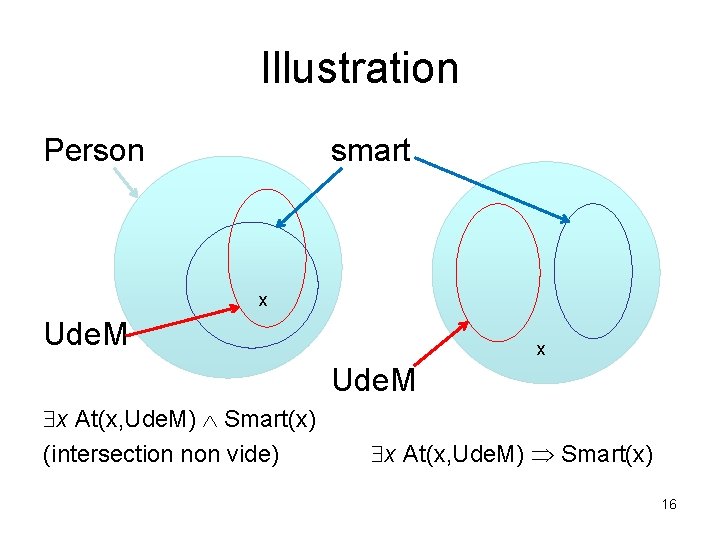
Illustration Person smart x Ude. M x At(x, Ude. M) Smart(x) (intersection non vide) x At(x, Ude. M) Smart(x) 16

Quelques exemples • Toute personne est mortel. Socrate est une personne. x Personne(x) Mortel(x) Personne(Socrate) • Socrate est mortel. Mortel(Socrate) • IFT 3335 est un cours à Ude. M. Cours(IFT 3335) Donné_à(IFT 3335, Ude. M) ou Cours(IFT 3335, Ude. M) Cours(IFT 3335) Donné_à(IFT 3335, Ude. M)? –Il faut standardiser les prédicats • Tous ceux qui suivent le cours IFT 3335 sont des étudiants à Ude. M. –Ceux qui suivent le cours IFT 3335: x Suivre(x, IFT 3335) Cours(IFT 3335) –Étudiants à Ude. M: Étudiant(x, Ude. M) –Toute la phrase: x Suivre(x, IFT 3335) Cours(IFT 3335) Étudiant(x, Ude. M) 17

Quelques exemples • Certains dans le cours IFT 3335 sont des étudiants à Ude. M. x Suivre(x, IFT 3335) Cours(IFT 3335) Étudiant(x, Ude. M) • Propriété: Jean est un étudiant. –Étudiant(Jean) –Ou x Étudiant(Jean, x) • Négation: Aucun est irremplaçable. – x Personne(x) Remplaçable(x) ? 18

Propriétés des quantificateurs • x y est équivalent à y x • x y n’est pas équivalent às y x • x y Loves(x, y) – “There is a person who loves everyone in the world” • y x Loves(x, y) – “Everyone in the world is loved by at least one person” • Dualité de quantificateurs: chacun peut être exprimé en utilisant l’autre: x P = x P, x P = x P – x Likes(x, Ice. Cream) – x Likes(x, Broccoli) x Likes(x, Ice. Cream) x Likes(x, Broccoli) 19

Égalité • terme 1 = terme 2 est vrai sous une interprétation donnée ssi terme 1 et terme 2 réfèrent au même objet (= est un prédicat spécial) • E. g. , définition de Sibling en terme de Parent: x, y Sibling(x, y) [ (x = y) m, f (m = f) Parent(m, x) Parent(f, x) Parent(m, y) Parent(f, y)] 20

Utiliser LPO pour décrire le monde Le domaine de parenté: • Brothers are siblings x, y Brother(x, y) Sibling(x, y) • One's mother is one's female parent m, c Mother(c) = m (Female(m) Parent(m, c)) • “Sibling” is symmetric x, y Sibling(x, y) Sibling(y, x) 21

Utiliser LPO Le domaine des ensembles: • s Set(s) (s = {} ) ( x, s 2 Set(s 2) s = {x|s 2}) • x, s {x|s} = {} • x, s x s s = {x|s} • x, s x s [ y, s 2 (s = {y|s 2} (x = y x s 2))] • s 1, s 2 s 1 s 2 ( x x s 1 x s 2) • s 1, s 2 (s 1 = s 2) (s 1 s 2 s 1) • x, s 1, s 2 x (s 1 s 2) (x s 1 x s 2) 22

Interagir avec une base de connaissances en LPO • Supposons que l’agent dans le monde de wumpus utilise une base de connaissances (KB) en LPO. Il perçoit une odeur et une brise (mais pas de scintillement) à t=5: Tell(KB, Percept([Smell, Breeze, None], 5)) Ask(KB, a Best. Action(a, 5)) (note: a est une variable) • I. e. , Est-ce que la KB entraîne une certaine meilleure action à t=5? • Réponse: Yes, {a/Shoot} ← substitution (binding list) • Étant donné une phrase S et une substitution σ, • Sσ dénote le résultat de l’application de σ sur S; e. g. , S = Smarter(x, y) σ = {x/Hillary, y/Bill} Sσ = Smarter(Hillary, Bill) • Ask(KB, S) retourne une/toute σ telle que KB╞ σ 23

Substitution • Remplacer une variable par un terme (constante, variable, ou fonction) x/Terme – {x/Hillary, y/Bill} – {x/y, z/Bill} – {x/Mère_de(z), y/Père_de(z)} • Contraintes – x ne doit pas apparaître dans Terme substituant • {x/Mère_de(x)} X – Une variable ne peut pas être substituée 2 fois • {x/Jean, x/Philippe} X • Sert à instancier une expression générale (contenant des variables) et à unifier deux expressions (voir plus tard) 24

Application d’une substitution • x/Terme: Remplacer toutes occurrences de la variable par le Terme e. g. Smarter(x, z) {x/y, z/Bill} : Smarter(y, Bill) Smarter(x, y) {x/y, z/Bill} : Smarter(y, y) (Smarter(x, z) President(z, c) Country(c) ) {x/y, z/Bill}: Smarter(y, Bill) President(Bill, c) Country(c) • Composition des substitutions σ1 ● σ2: appliquer σ1 ensuite σ2 = appliquer σ2 sur σ1 et faire l’union avec σ2 e. g. {y/z, x/Bill} ● {z/Hillary, v/Chelsea} = {y/Hillary, x/Bill} {z/Hillary, v/Chelsea} = {y/Hillary, x/Bill, z/Hillary, v/Chelsea} 25

Pourquoi substitution? • À causes des variables • Exemple Tout homme est mortel. Socrate est un homme. Donc, Socrate est mortel. x Homme(x) Mortel(x) Homme(Socrate) Mortel(Socrate) σ={x/Socrate} Homme(Socrate) Mortel(Socrate) Homme(Socrate) Mortel(Socrate) 26

Base de conaissances pour le monde de wumpus • Perception – t, s, b Percept([s, b, Glitter], t) Glitter(t) • Réflex – t Glitter(t) Best. Action(Grab, t) • Note: variables exprimer une connaissance générale sur un ensemble d’objets (carrés, temps, etc. ) 27

Déduire les propriétés cachées • x, y, a, b Adjacent([x, y], [a, b]) [a, b] {[x+1, y], [x-1, y], [x, y+1], [x, y-1]} Propriétés des carrés (avec temps t): • s, t At(Agent, s, t) Breeze(t) Breezy(s) Les carrés à coté d’une fosse sont odorantes (smelly): – Règle de diagnostic ---effet cause s Breezy(s) r Adjacent(r, s) Pit(r) – Règle causale --- cause effet r Pit(r) [ s Adjacent(r, s) Breezy(s) ] 28

Remarque: Que signifie “premier ordre”? • On peut utiliser une variable pour représenter des objets seulement • Pas de variable pour des prédicats ou des fonctions – x y Personne(x) y(x, USA) – Il y a une personne (x) qui a une certaine relation (y) avec USA – Logique du second ordre – Certaines de ces expressions du second ordre peuvent être réécrites en expressio du premier ordre • E. g. Relation(x, USA, y) 29

Ingénierie de connaissances dans LPO 1. Identifier la tâche 2. Assembler les connaissances pertinentes 3. Décider sur le vocabulaire de prédicats, de fonctions et de constantes 4. Encoder les connaissances générales dans le domaine 5. Encoder une description de l’instance spécifique du problème 6. Poser des questions à la procédure d’inférence et obtenir des réponses 7. Debugger la base de connaissances 30

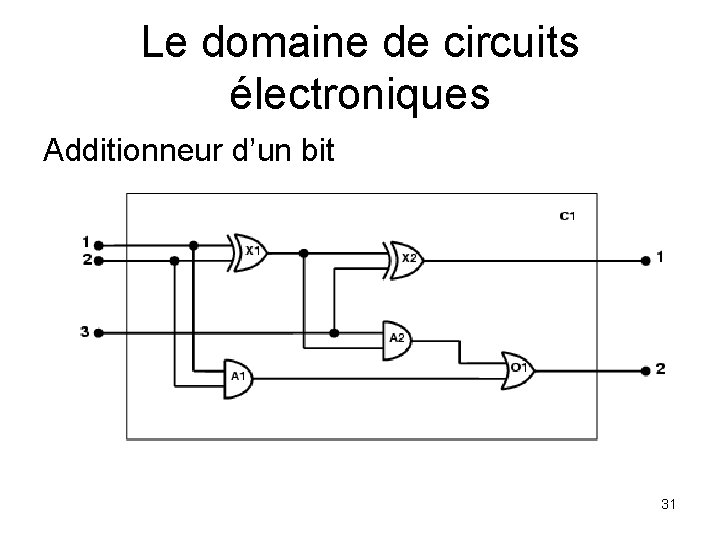
Le domaine de circuits électroniques Additionneur d’un bit 31

Le domaine de circuits électroniques 1. Identifier la tâche – Est-ce que le circuit additionne correctement? (vérification de circuit ) 2. Assembler les connaissances pertinentes – Des circuits composés de fils et de portes; Types de portes (AND, OR, XOR, NOT) – Non pertinents: taille, forme, couleur, coût de portes 3. Décider sur le vocabulaire – Alternatives: Type(X 1) = XOR Type(X 1, XOR) XOR(X 1) 32

Le domaine de circuits électroniques 4. Encoder les connaissances générales du domaine – – – – t 1, t 2 Connected(t 1, t 2) Signal(t 1) = Signal(t 2) t Signal(t) = 1 Signal(t) = 0 1≠ 0 t 1, t 2 Connected(t 1, t 2) Connected(t 2, t 1) g Type(g) = OR Signal(Out(1, g)) = 1 n Signal(In(n, g)) = 1 g Type(g) = AND Signal(Out(1, g)) = 0 n Signal(In(n, g)) = 0 g Type(g) = XOR Signal(Out(1, g)) = 1 Signal(In(1, g)) ≠ Signal(In(2, g)) g Type(g) = NOT Signal(Out(1, g)) ≠ Signal(In(1, g)) 33

Le domaine de circuits électroniques 5. Encoder l’instance spécifique du problème Type(X 1) = XOR Type(A 1) = AND Type(O 1) = OR Type(X 2) = XOR Type(A 2) = AND Connected(Out(1, X 1), In(1, X 2)) Connected(Out(1, X 1), In(2, A 2)) Connected(Out(1, A 2), In(1, O 1)) Connected(Out(1, A 1), In(2, O 1)) Connected(Out(1, X 2), Out(1, C 1)) Connected(Out(1, O 1), Out(2, C 1)) Connected(In(1, C 1), In(1, X 1)) Connected(In(1, C 1), In(1, A 1)) Connected(In(2, C 1), In(2, X 1)) Connected(In(2, C 1), In(2, A 1)) Connected(In(3, C 1), In(2, X 2)) Connected(In(3, C 1), In(1, A 2)) 34

Le domaine de circuits électroniques 6. Poser des questions à la procédure d’inférence – Quels sont les ensembles de valeurs possibles de tous les terminaux pour le circuit additionneur? i 1, i 2, i 3, o 1, o 2 Signal(In(1, C 1)) = i 1 Signal(In(2, C 1)) = i 2 Signal(In(3, C 1)) = i 3 Signal(Out(1, C 1)) = o 1 Signal(Out(2, C 1)) = o 2 7. Debugger la base de connaissances – Peut oublier des affirmations (assertions) comme 1 ≠ 0 35

Sommaire • Logique du premier ordre: – Objets et relations sont des primitives sémantiques – syntaxe: constantes, fonctions, prédicats, égalité, quantificateurs • Capacité d’expression plus grande: suffisant pour définir le monde de wumpus 36