36 th seminar Chap 1 Chap 2 Chap

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 1/21 Synthesis of Constrained Robust Predictive Controller for Energy Management of Multiple Energy Sources in Hybrid Electric Vehicle Han, Jihun System Dynamics and Applied Control Laboratory Center for Noise and Vibration Control KAIST 2015. 06. 05 Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

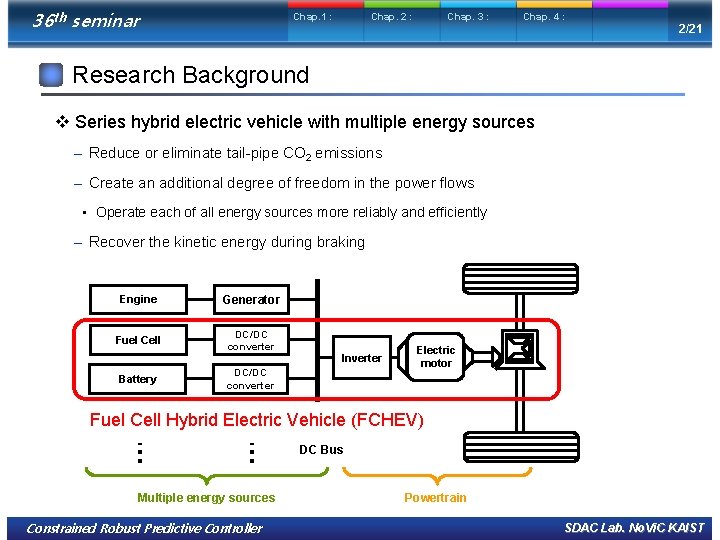
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 2/21 Research Background v Series hybrid electric vehicle with multiple energy sources – Reduce or eliminate tail-pipe CO 2 emissions – Create an additional degree of freedom in the power flows • Operate each of all energy sources more reliably and efficiently – Recover the kinetic energy during braking Engine Generator Fuel Cell DC/DC converter Battery Inverter DC/DC converter Electric motor DC/DC Ultracapacitor Fuel Cell Hybrid Electric converter Vehicle (FCHEV) … … Multiple energy sources Constrained Robust Predictive Controller DC Bus Powertrain SDAC Lab. No. Vi. C KAIST

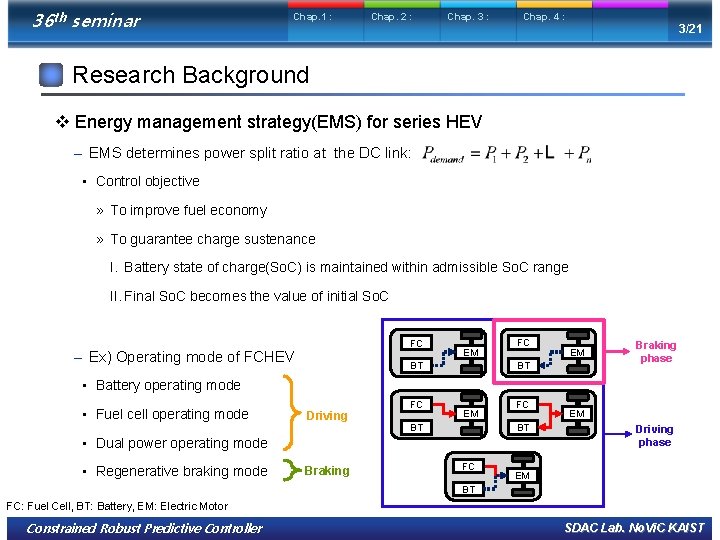
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 3/21 Research Background v Energy management strategy(EMS) for series HEV – EMS determines power split ratio at the DC link: • Control objective » To improve fuel economy » To guarantee charge sustenance I. Battery state of charge(So. C) is maintained within admissible So. C range II. Final So. C becomes the value of initial So. C FC – Ex) Operating mode of FCHEV EM FC EM BT BT Braking phase • Battery operating mode • Fuel cell operating mode Driving FC EM BT FC BT • Dual power operating mode • Regenerative braking mode Braking FC EM Driving phase EM BT FC: Fuel Cell, BT: Battery, EM: Electric Motor Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 4/21 Research Background v Real-world driving situation – Hilly roads are prevalent – Future driving information can be predicted by using GPS*, GIS**, and ITS*** Current position GPS Driver Altitude Future geological information GIS Final destination : Planned route Distance Extraction of altitude profile Velocity ITS Trip information (speed limits, congestion level, traffic signal and etc) E M S Distance Prediction of velocity profile *GPS: Global Positioning Systems, **GIS: Geographic Information Systems, ***ITS: Intelligent Transportation Systems Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

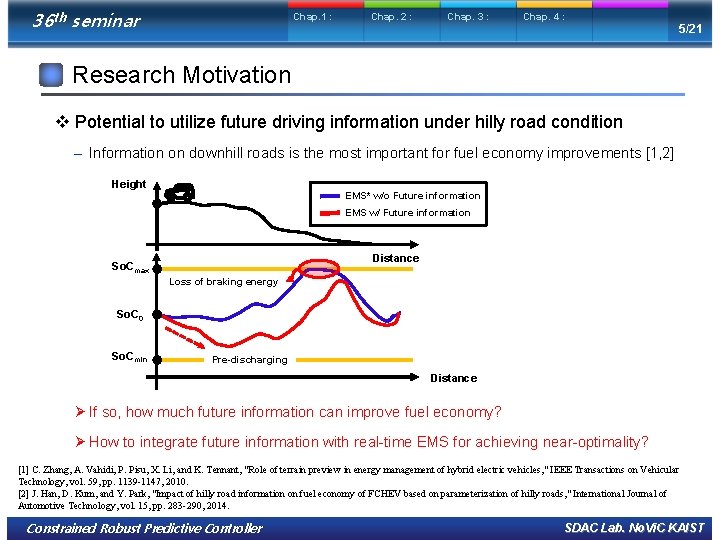
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 5/21 Research Motivation v Potential to utilize future driving information under hilly road condition – Information on downhill roads is the most important for fuel economy improvements [1, 2] Height EMS* w/o Future information EMS w/ Future information Distance So. Cmax Loss of braking energy So. C 0 So. Cmin Pre-discharging Distance Ø If so, how much future information can improve fuel economy? Ø How to integrate future information with real-time EMS for achieving near-optimality? [1] C. Zhang, A. Vahidi, P. Pisu, X. Li, and K. Tennant, "Role of terrain preview in energy management of hybrid electric vehicles, " IEEE Transactions on Vehicular Technology, vol. 59, pp. 1139 -1147, 2010. [2] J. Han, D. Kum, and Y. Park, "Impact of hilly road information on fuel economy of FCHEV based on parameterization of hilly roads, " International Journal of Automotive Technology, vol. 15, pp. 283 -290, 2014. Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 6/21 Research Objective v Quantify maximum fuel economy improvement – Define and calculate the benefits of future information on fuel economy improvement for various driving conditions v Analyze deterministic offline-generated control strategy – Extract insights to design real-time predictive controller in terms of near-optimal performance within deterministic environment v Analyze stochastic offline-generated control strategy – Extract insights to design real-time predictive controller in terms of robust performance toward driving uncertainty within stochastic environment v Synthesize and evaluate robust predictive EMS – Compare several EMSs for validation Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

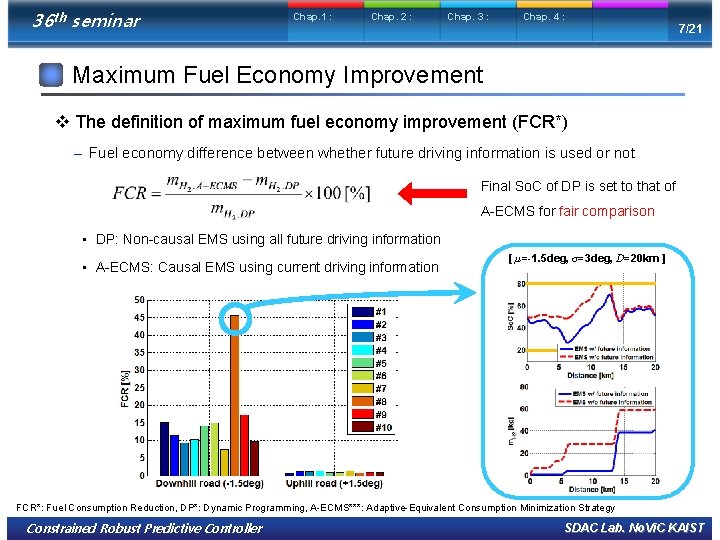
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 7/21 Maximum Fuel Economy Improvement v The definition of maximum fuel economy improvement (FCR*) – Fuel economy difference between whether future driving information is used or not Final So. C of DP is set to that of A-ECMS for fair comparison • DP: Non-causal EMS using all future driving information • A-ECMS: Causal EMS using current driving information [ µ=-1. 5 deg, σ=3 deg, D=20 km ] FCR*: Fuel Consumption Reduction, DP*: Dynamic Programming, A-ECMS***: Adaptive-Equivalent Consumption Minimization Strategy Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

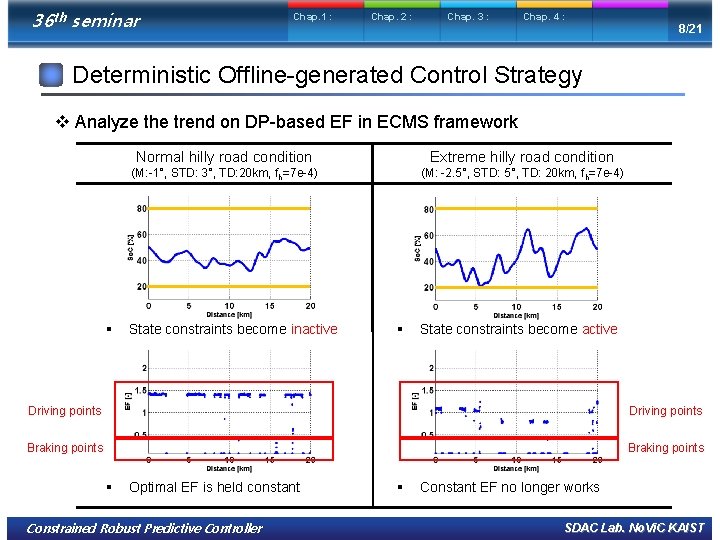
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 8/21 Deterministic Offline-generated Control Strategy v Analyze the trend on DP-based EF in ECMS framework § Normal hilly road condition Extreme hilly road condition (M: -1°, STD: 3°, TD: 20 km, fh=7 e-4) (M: -2. 5°, STD: 5°, TD: 20 km, f h=7 e-4) State constraints become inactive § State constraints become active Driving points Braking points § Optimal EF is held constant Constrained Robust Predictive Controller § Constant EF no longer works SDAC Lab. No. Vi. C KAIST

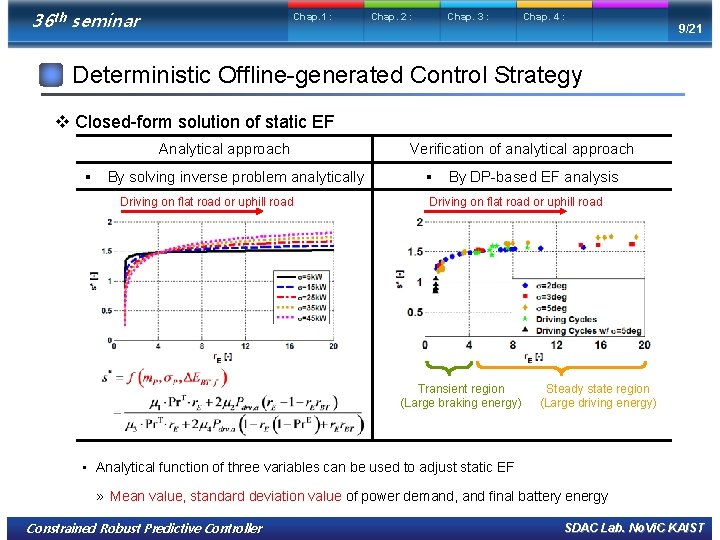
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 9/21 Deterministic Offline-generated Control Strategy v Closed-form solution of static EF Analytical approach Verification of analytical approach § By solving inverse problem analytically § By DP-based EF analysis Driving on flat road or uphill road Transient region (Large braking energy) Steady state region (Large driving energy) • Analytical function of three variables can be used to adjust static EF » Mean value, standard deviation value of power demand, and final battery energy Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 10/21 Stochastic Offline-generated Control Strategy v Deterministic optimal control VS stochastic optimal control – Ex. ) Stochastic DP and PMP • Stochastic differential equation: x is stochastic process » Itô’s Lemma and Itô’s integral Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 11/21 Stochastic Offline-generated Control Strategy v Given stochastic differential equation – Based on Brownian motion (W): ξ(t) is defined as stationary white noise – Itô’s Lemma • Another process Y(t) which is a function of X(t): Y(t)=φ(t, X(t)) where, the function Y(t) is continuously • Stochastic differential equation for the Y(t) differentiable in t and twice continuously differentiable in X – Itô’s integral • Integral of a stochastic process w. r. t. the Brownian motion W(t, ω) on the interval [0, T] Riemann sum where 0=t 0<t 1<…<t. N-1<t. N<T Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 12/21 Stochastic Offline-generated Control Strategy v Stochastic Hamilton-Jacobi-Bellman (HJB) Equation – Steps for solving stochastic optimal control problem • By removing the stochastic integral and subtracting J(x, t) on both sides • Finally, stochastic HJB equation for stochastic process is expressed as follows: Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 13/21 Stochastic Offline-generated Control Strategy v Stochastic Pontryagin’s minimum principle (PMP) – Derivation of the stochastic PMP based on HJB equation for stochastic process • Definition of the co-state variables • Stochastic Hamiltonian function • HJB equation for stochastic process » By taking derivative of HJB equation w. r. t. x » Itô’s Lemma is also applied to express the derivation of the co-state as follows: Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 14/21 Stochastic Offline-generated Control Strategy v Stochastic Pontryagin’s minimum principle (PMP) – Derivation of the stochastic PMP based on HJB equation for stochastic process • To obtain an expression for the dynamics of px (Jxx) » By taking second-order derivative of HJB equation w. r. t. x » Itô’s Lemma is also applied to express the derivation of px (Jxx) Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 15/21 Stochastic Offline-generated Control Strategy v Stochastic Pontryagin’s minimum principle (PMP) – Summary Stochastic PMP Constrained Robust Predictive Controller Deterministic PMP SDAC Lab. No. Vi. C KAIST

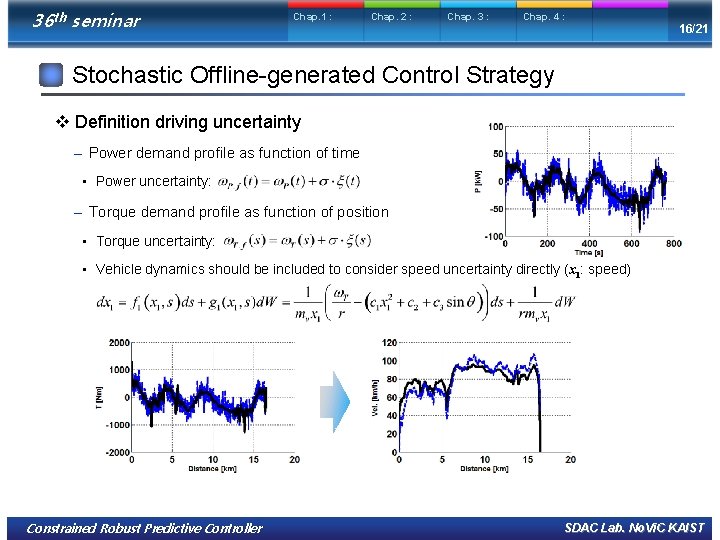
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 16/21 Stochastic Offline-generated Control Strategy v Definition driving uncertainty – Power demand profile as function of time • Power uncertainty: – Torque demand profile as function of position • Torque uncertainty: • Vehicle dynamics should be included to consider speed uncertainty directly (x 1: speed) Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 17/21 Stochastic Offline-generated Control Strategy v Stochastic system dynamics in position domain – Driver torque demand with perturbation • State 1 (Velocity): • State 2 (Battery So. C): • State 3 for considering upper/lower bound on State 2 Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 18/21 Stochastic Offline-generated Control Strategy v Stochastic system dynamics in position domain – Expected Hamiltonian function – Optimal control input Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 19/21 Stochastic Offline-generated Control Strategy v Stochastic system dynamics in position domain – First-order co-state dynamics – Second-order co-state dynamics Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

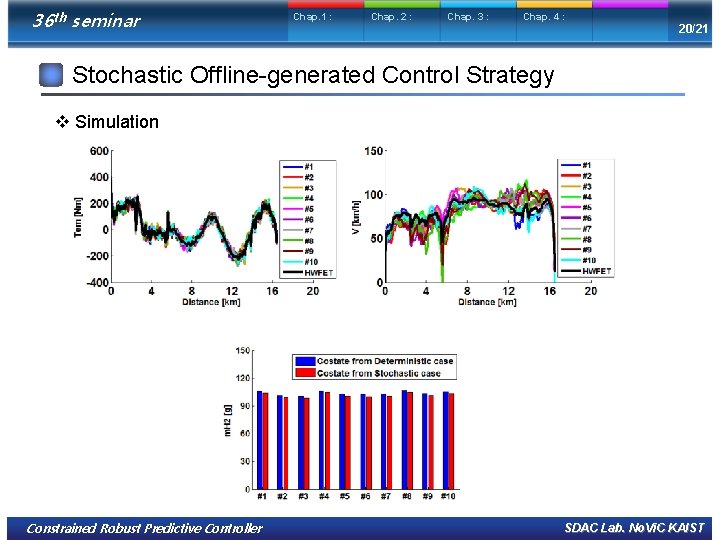
36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 20/21 Stochastic Offline-generated Control Strategy v Simulation Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : 21/21 Future works v Simulation for several driving conditions – Check robustness within stochastic environment – Compare offline-generated control strategy from deterministic case v Design and implementation of real-time controller – Simulation Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST

36 th seminar Chap. 1 : Chap. 2 : Chap. 3 : Chap. 4 : Q&A Thank you Q&A Constrained Robust Predictive Controller SDAC Lab. No. Vi. C KAIST