Entscheidungsrechnungen bei Unsicherheit EwertWagenhofer 2008 Alle Rechte vorbehalten

Entscheidungsrechnungen bei Unsicherheit © Ewert/Wagenhofer 2008. Alle Rechte vorbehalten!

Ziele n Darstellung der Vorgehensweise bei der Break Even-Analyse n Analyse der Auswirkungen von Unsicherheit auf die Produktionsprogrammplanung n Aufzeigen der Entscheidungsrelevanz von Fixkosten unter verschiedensten Bedingungen 5. 2

Motivation n Gründe für Annahme sicherer Erwartungen bei KLR dient kurzfristig wirksamen Entscheidungen m Erläuterung grundlegender Prinzipien m n Gegenargument m n Stimmigkeit obiger Argumente erst nach Analyse unter Einbeziehung der Unsicherheit beurteilbar Einbeziehung von Unsicherheit Behandelte Ansätze Break Even-Analyse l Modellansätze für kurzfristig wirksame Entscheidungen und Lösungsstrukturen am Beispiel von Produktionsprogrammentscheidungen l Besondere Fragen dabei Messung von Risiko l Entscheidungskontext: z. B Handelbarkeit des Eigenkapitals l Entscheidungsrelevanz von Fixkosten l 5. 3

Break Even-Analyse Grundlagen n Grundidee l Einfluss von exogenen Parametern auf die Lösung von Entscheidungsproblemen n Methode: Sensitivitätsanalyse l Empfindlichkeit der Zielgrößen auf Änderungen der Parameter l Ermittlung des “günstigen” Parameterbereichs: Entscheidung bleibt optimal n Grundmodell der Break Even-Analyse Fokus auf Beschäftigungsunsicherheit l Ermittlung einer Break Even-Menge l Ermittlung anderer kritischer Parameterwerte möglich 5. 4

BEA im Einproduktfall Bestimmung des Periodengewinns mit d k p x KF Deckungsbeitrag variable Stückkosten je Produkteinheit Absatzpreis je Produkteinheiten Fixkosten 5. 5
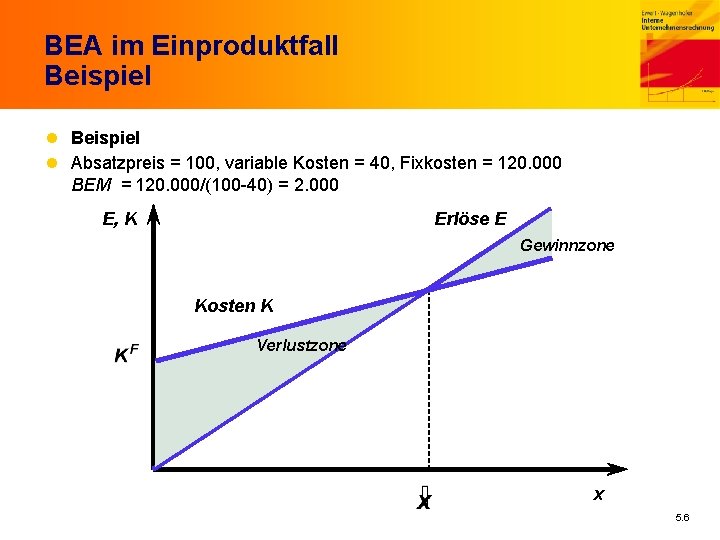
BEA im Einproduktfall Beispiel l Absatzpreis = 100, variable Kosten = 40, Fixkosten = 120. 000 BEM = 120. 000/(100 -40) = 2. 000 E, K Erlöse E Gewinnzone Kosten K Verlustzone x 5. 6
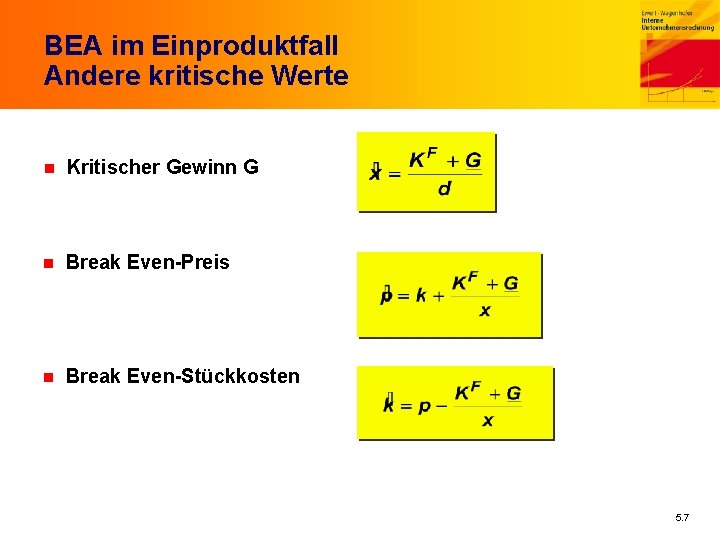
BEA im Einproduktfall Andere kritische Werte n Kritischer Gewinn G n Break Even-Preis n Break Even-Stückkosten 5. 7

BEA im Einproduktfall Fortsetzung Beispiel Fixkosten = 120. 000 Absatzpreis = 100 variable Kosten = 40 Menge = 1. 800 kritischer Gewinn = 0 Break Even-Preis = 40 + 120. 000/1. 800 = 106, 67 für Absatzpreis = 90 Break Even-Stückkosten = 90 - 120. 000/1. 800 = 23, 22 Für Absatzpreis = 80 Break Even-Stückkosten = 80 - 120. 000/1. 800 = 13, 33 5. 8
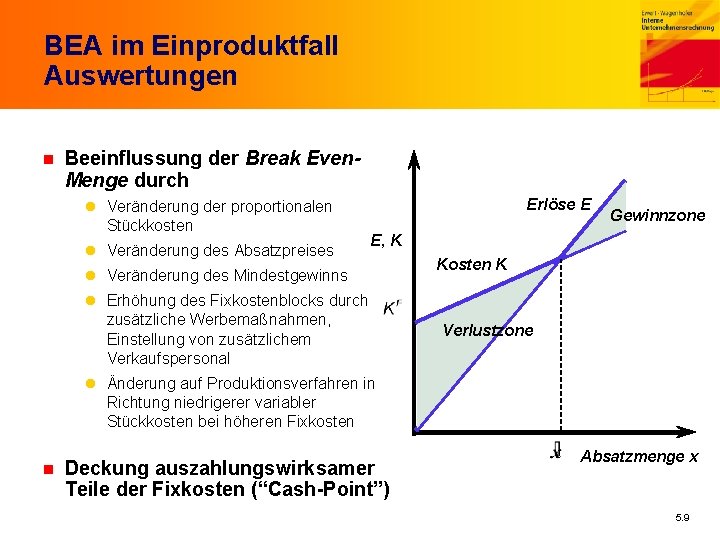
BEA im Einproduktfall Auswertungen n Beeinflussung der Break Even. Menge durch l Veränderung der proportionalen Stückkosten l Veränderung des Absatzpreises Erlöse E Gewinnzone E, K l Veränderung des Mindestgewinns l Erhöhung des Fixkostenblocks durch zusätzliche Werbemaßnahmen, Einstellung von zusätzlichem Verkaufspersonal Kosten K Verlustzone l Änderung auf Produktionsverfahren in Richtung niedrigerer variabler Stückkosten bei höheren Fixkosten n Deckung auszahlungswirksamer Teile der Fixkosten (“Cash-Point”) Absatzmenge x 5. 9

Risikomaße Sicherheitskoeffizient SK n Fragestellung l Um welchen Prozentsatz darf Umsatz/Absatz (ausgehend von Basiswert) sinken, ohne in die Verlustzone zu geraten? n Überlegungen l Je höher SK, desto sicherer positiver/bestimmter Periodenerfolg l Ausgangsmenge x: volle Kapazitätsauslastung Beispiel Kapazität x = 10. 000, BE-Menge = 8. 000 Sicherheitskoeffizient = 1 - 8. 000/10. 000 = 0, 2 Kapazitätsauslastung kann um 20% unterschritten werden, ehe man Verluste macht 5. 10
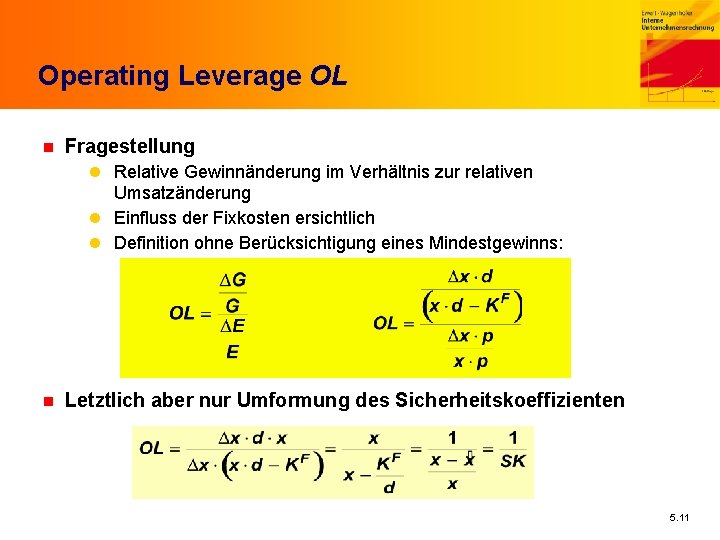
Operating Leverage OL n Fragestellung l Relative Gewinnänderung im Verhältnis zur relativen Umsatzänderung l Einfluss der Fixkosten ersichtlich l Definition ohne Berücksichtigung eines Mindestgewinns: n Letztlich aber nur Umformung des Sicherheitskoeffizienten 5. 11

Beurteilung von SK und OL n Problem: Keine Berücksichtigung der Verteilungen Darstellung am Beispiel der Gewinnvarianz n Wirkungen Tatsächlich Niedrigere Stückkosten führen zu höherem Deckungsbeitrag und höherer Varianz des Gewinns l Fixkosten ohne Konsequenzen für Varianz l Kennzahlen Niedrigere Stückkosten führen zu höherem Deckungsbeitrag, zu geringerer BEM und zu höherem SK und niedrigerem OL l Höhere Fixkosten führen zu größerem OL l 5. 12

Beispiel n n Varianz der Absatzmengen: 150 Absatzpreis: 10 Verfahren 1: Verfahren 2: Gleiche Werte für SK und OL Gewinnvarianzen Verfahren 1: Verfahren 2: 5. 13

Vergleich mit dem Variationskoeffizienten VK Hier gilt Diese Beziehungen sind analog zu denjenigen bei SK und OL 5. 14

Stochastische Break Even-Analyse Einproduktfall n Explizite Untersuchung der Wahrscheinlichkeitsverteilung des Gewinns l Verteilung der einzelnen Bestimmungsfaktoren n n Annahme risikobehafteter Absatzmengen Risiko als Wahrscheinlichkeit für Erfolgsniveau G Break Even-Wahrscheinlichkeit 5. 15

Stochastische Break Even-Analyse Beispiel Absatzmengen x seien gleichverteilt im Intervall Break Even-Wahrscheinlichkeit 5. 16
![Stochastische Break Even-Analyse Beispiel. . . Absatzmengen gleichverteilt in [0, 10. 000] F(x) = Stochastische Break Even-Analyse Beispiel. . . Absatzmengen gleichverteilt in [0, 10. 000] F(x) =](http://slidetodoc.com/presentation_image_h/2778cdeb30f543e3ae9811fb9f006a09/image-17.jpg)
Stochastische Break Even-Analyse Beispiel. . . Absatzmengen gleichverteilt in [0, 10. 000] F(x) = 0, 0001 x Deckungsbeitrag d = 50, Fixkosten = 200. 000 Break Even-Menge = 4. 000 F(4. 000) = 0, 4 und Break Even-Wahrscheinlichkeit = 0, 6 Wahrscheinlichkeit n 0 4. 000 10. 000 Menge 5. 17

Stochastische Break Even-Analyse Weitere Fragestellung n Fragestellung l Wie hoch ist der maximale Erfolg, der mit einer vorgegebenen Wahrscheinlichkeit überschritten wird? 5. 18

Stochastische Break Even-Analyse Beispiel n Maximierung der Break Even-Wahrscheinlichkeit Annahmen: Absatzmengen gleichverteilt in [0, 10. 000] Deckungsbeitrag d = 40 Fixkosten = 150. 000 Variante: g Verkaufspersonal mit Fixkosten = 90. 000 Obergrenze Absatzmenge = 13. 000 Mindestgewinn = 200. 000 n Einstellun und Ausgangssituation: erforderlicher Absatz = 8. 750; Wahrscheinlichkeit 0, 125 Variante: erforderlic her Absatz = 11. 000; 5. 19 Wahrschei

Stochastische Break Even-Analyse Beispiel. . . n Fragestellung: Ergebnismaximierung bei vorgegebener Wahrscheinlichkeit Vorgegebene Wahrscheinlichkeit = 0, 4 n Ausgangssituation G = 40[10. 000 - 0, 4(10. 000 - 0)] - 150. 000 = 90. 000 Variante G = 40[13. 000 - 0, 4(13. 000 - 0)] - 240. 000 = 72. 000 Einstellung zusätzlichen Verkaufspersonals unvorteilhaft 5. 20

Simulationsverfahren 1. Auswahl als unsicher betrachteter Parameter (P) 2. Schätzung isolierter Wahrscheinlichkeiten für jeden P 3. Ermittlung der Ausgangsgrößen für Simulationslauf m. Zufallszahlen für jeden P gleichverteilt in [0, 1] m. Transformation in konkreten Parameterwert m. Berücksichtigung stochastischer Abhängigkeiten durch sukzessives Vorgehen 4. Berechnung der Zielgröße 5. Häufige Wiederholung von 3. und 4. (z. B 10. 000 mal) 6. Ermittlung der Verteilungsfunktion der Zielgröße aus relativen Häufigkeiten 5. 21
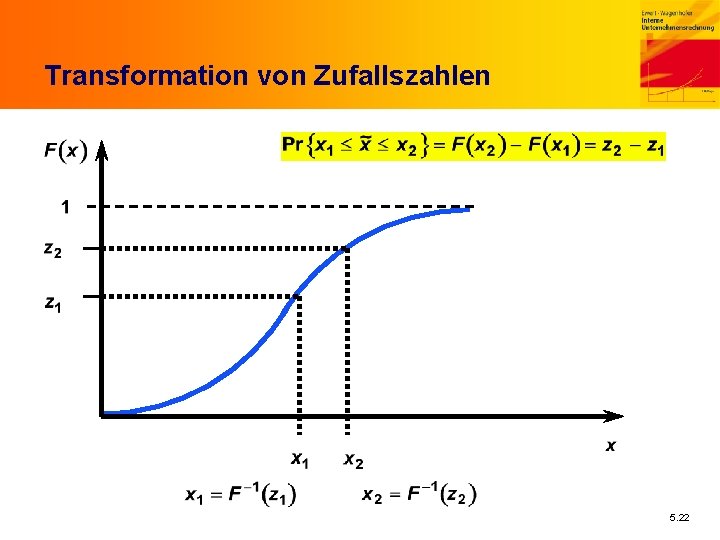
Transformation von Zufallszahlen 5. 22

Value-at-Risk und Cash-Flow-at-Risk n n Risikomaße im praktischen Risikomanagement Value-at-Risk (Va. R) l Downside-Risikomaß l Probleme bei Anwendung im Nichtbankenbereich n Cash-Flow-at-Risk (CFa. R) l Berücksichtigt Besonderheiten im Nichtbankenbereich 5. 23

Break Even-Analyse Mehrproduktfall n n n Ausgleichseffekte zwischen verschiedenen Produktarten Produktionsprogramm soll in seiner Gesamtheit ein bestimmtes Ergebnis bescheren Nicht mehr eine Break Even-Menge, sondern eine Vielzahl von Mengenkombinationen l Absatzmengenkombinationen der Produktarten j = 1, . . . , J: 5. 24

Break Even-Analyse Mehrproduktfall. . . n Zweiproduktfall: Gerade n Mehrproduktfall: Konvexkombination isolierter Break Even-Mengen 5. 25

Break Even-Analyse: Mehrproduktfall Beispiel n J = 4 Produktarten Deckungsbeiträge: d 1 = 20; d 2 = 70; d 3 = 60; d 4 = 150 Fixkosten = 150. 000 Mindestgewinn = 60. 000 Break Even-Mengen Beliebiger Break Even-Vektor 5. 26

Break Even-Analyse Mehrproduktfall. . . Konstanter Absatzmix n n Beliebiges Produkt als Leitprodukt Annahme konstanter Verhältnisse der Absatzmengen l Für erstes Produkt als Leitprodukt und bj als konstante Verhältnisse der Absatzmengen der Produkte j zu Produkt 1 5. 27
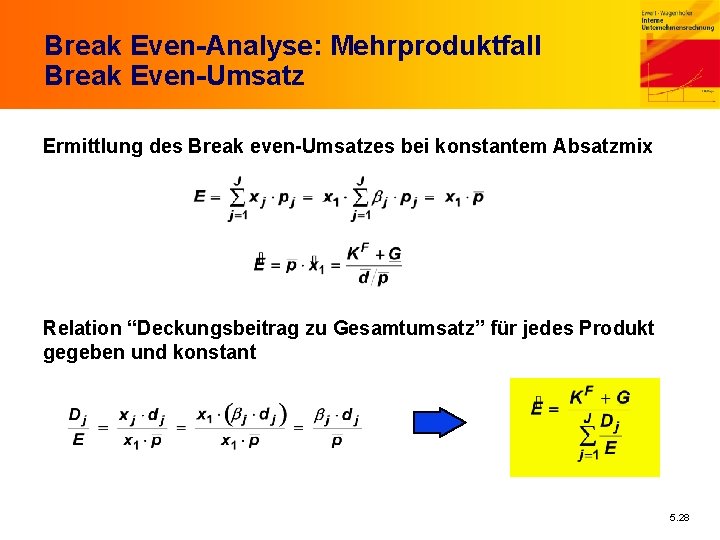
Break Even-Analyse: Mehrproduktfall Break Even-Umsatz Ermittlung des Break even-Umsatzes bei konstantem Absatzmix Relation “Deckungsbeitrag zu Gesamtumsatz” für jedes Produkt gegeben und konstant 5. 28

Break Even-Analyse: Mehrproduktfall Beispiel Mengenrelation 1 : 2 : 4 5. 29

Break Even-Analyse: Mehrproduktfall Beispiel. . . Mengenrelation 1: 2: 4: 4 Gegeben seien folgende Preise 5. 30
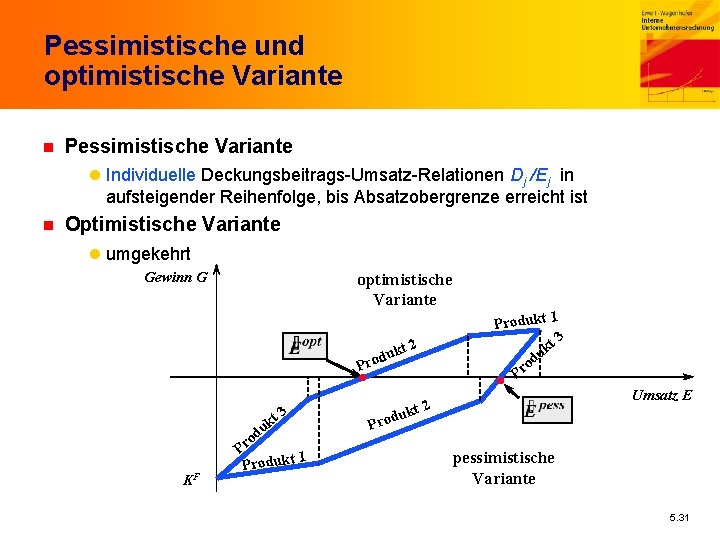
Pessimistische und optimistische Variante n Pessimistische Variante l Individuelle Deckungsbeitrags-Umsatz-Relationen Dj /Ej in aufsteigender Reihenfolge, bis Absatzobergrenze erreicht ist n Optimistische Variante l umgekehrt Gewinn G optimistische Variante uk rod t 2 P kt u d KF 3 o Pr 1 Produkt Pro 1 Produkt t 3 k du o Pr Umsatz E kt 2 du pessimistische Variante 5. 31

Break Even-Analyse Ergebnis n BEA vermittelt Gefühl für Bedeutung der Unsicherheit n BEA als wichtige Signalfunktion insbes für mehr Informationsbeschaffungen bzw Planungsansätze unter expliziter Einbeziehung von Wahrscheinlichkeitsverteilungen n Keine konkrete Handlungsempfehlung n Erfordernis expliziter Analyse der Konsequenzen verschiedener Problemstrukturen für die Unternehmenspolitik 5. 32

Programmplanung bei Risiko n Untersuchung der Implikationen expliziter Risikoberücksichtigung in der Produktionsprogrammplanung l Bestehen Unterschiede in der Lösungsstruktur n Was ist risikobehaftet? Risikobehaftete Beschaffungs- oder Absatzpreise (Deckungsbeitrag) Risikobehaftete Fixkosten n Annahmen im folgenden l Eine Mehrproduktrestriktion, die nicht risikobehaftet ist l Gesamtes Produktionsprogramm wird im voraus festgelegt 5. 33
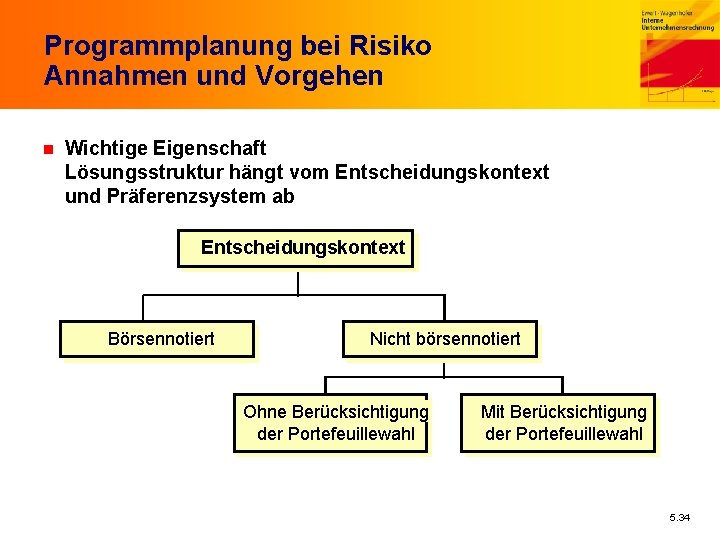
Programmplanung bei Risiko Annahmen und Vorgehen n Wichtige Eigenschaft Lösungsstruktur hängt vom Entscheidungskontext und Präferenzsystem ab Entscheidungskontext Börsennotiert Nicht börsennotiert Ohne Berücksichtigung der Portefeuillewahl Mit Berücksichtigung der Portefeuillewahl 5. 34

Börsennotierte Unternehmen Zielsystem n Marktwertmaximierung für börsennotierte Unternehmen als überragendes Ziel n Berechnung von Marktwerten l Time State Preference-Ansatz l Arbitrage Pricing Theory (APT) (Arbitragefreiheit im Marktgleichgewicht) 5. 35

Börsennotierte Unternehmen Marktannahmen n Spanning Eine Unternehmung kann durch ihre Entscheidungen keine “völlig neue” Rückflussstruktur schaffen. Die bestehenden Finanztitel am Kapitalmarkt spannen einen Vektorraum auf, der durch Investitions- und Produktionsentscheidungen eines betrachteten Unternehmens nicht verändert wird. n Competitivity Bewertungssystem am Kapitalmarkt wird durch Entscheidungen eines Unternehmens nicht verändert. Entspricht der Annahme eines konstanten Zinssatzes im Rahmen der Kapitalwertmaximierung bei sicheren Erwartungen 5. 36

Programmplanung bei Risiko Vorgehensweise l l Planungszeitraum von T Perioden Zahlungsüberschüsse Ü am Periodenende risikobehaftet durch Zustände q(t) Zustandsraum für Periode t. . . Q(t) Für jeden Zustand positiver Bewertungsfaktor R(q(t)) l Marktwert genau einer anfallenden Geldeinheit aus Sicht t = 0 l Marktwert W zu t = 0 Bewertungsfaktoren R(q(t)) beinhalten l Zeit- und Risikopräferenzen der Kapitalmarktteilnehmer l Erwartungen der Kapitalmarktteilnehmer l Zinssatz i für sichere Anlagen Marktwert einer in t = 1 mit Sicherheit erzielten Geldeinheit 5. 37

Programmplanung bei Risiko Wertadditivität n Kurzfristig wirksame Entscheidungen betrachtet Marktwerte der in t = 1 anfallenden Überschüsse n Zugrundegelegte Bewertungsfunktion “Wertadditivität” 5. 38

Beispiel Zustand q 1 Überschuss Ü(q) 100 Bewertungsfaktor R(q) 0, 3 q 2 q 3 200 0, 25 300 0, 25 5. 39

Programmplanung bei Risiko Interpretation der Bewertungsfaktoren n Time State Preference-Modell l Einperiodiges Portefeuille eines Investors l Vermögen V l Finanztitel j = 1, …, J Investor maximiert unter der Nebenbedingung Für den Konsum gilt: 5. 40

Programmplanung bei Risiko Interpretation der Bewertungsfaktoren ge-Funktion: Lagran Bedingungen erster Ordnung: Definiert man nun dann folgt 5. 41

Programmplanung bei Risiko Optimales Produktionsprogramm n Struktur des optimalen Produktionsprogramms l Nur Zahlungsüberschüsse können angesetzt werden l Stückdeckungsbeiträge sollen stets zahlungswirksam sein l Nur zahlungswirksame Fixkosten können relevant sein Lösungsstruktur Fixkosten irrelevant analog zu jener bei Sicherheit Verwendung von Marktwerten der Stück-DB statt sicherer Stück-DB Produkt mit höchstem spezifischen Marktwert des Stück-DB wird produziert 5. 42

Beispiel Produkt DB Stunden/Stk 1 je zu 50% 10 oder 20 5 2 14 5 Fixkosten = 0 Kapazität: 1. 400 Stunden R(q 1) = R(q 2) = 0, 4 Sicherer Zins = 25% Marktwerte Optimales Programm 280 Stück Produkt 1 5. 43

Beispiel. . . R(q 1) = 0, 6 R(q 2) = 0, 2 Sicherer Zins = 25% Marktwerte Optimales Programm Ausschließliche Produktion von Produkt 2 5. 44

Programmplanung bei Risiko Börsennotierte Unternehmen n Diversifikationsüberlegungen im Rahmen der Marktwertmaximierung (Risikoreduzierung) n In Marktwerten implizit andere Diversifikationsaspekte enthalten, die sich in Korrelation zu bestimmten Marktfaktoren manifestieren f(q). . . zustandsspezifische Eintrittswahrscheinlichkeiten n Erwartetes Erfolgsniveau wird korrigiert um Risikoterm, der Korrelation zu einem Marktfaktor widerspiegelt. Marktfaktor von Bewertungsfaktoren des gesamten Kapitalmarkts abhängig 5. 45

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (1) n n Zielgröße Subjektive Bewertung des Risikos durch einzelnen Entscheidungsträger Bernoulli-Prinzip: Erwartungsnutzenmaximierung l Subjektive Nutzenfunktion U für jeden Entscheidungsträger l Ergebnisgröße w: Endvermögen der Planungsperiode Endvermögen w = gegebenes Anfangsvermögen w 0 + Periodengewinn Gewählte Alternative ist jene mit dem größten Nutzenerwartungswert 5. 46

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (2) n Spezialfall Erwartungswertmaximierung l Nutzenfunktion U linear: U(w) = a + Rw mit R > 0 l Entscheider ist risikoneutral l Gesucht Produktionsprogramm mit maximalem (Perioden-)Gewinnerwartungswert Reihung nach dem höchsten erwarteten spezifischen DB Fixkosten sind irrelevant 5. 47

Beispiel Produkt 1 DB je zu 50% 10 oder 20 Stunden/St 5 erwarteter DB 15 2 14 5 14 Kapazität: 1. 400 Stunden Ausschließliche Produktion von Produkt 1 1. 400/5 = 280 Stück Erwarteter DB: 4. 200 5. 48

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (3) n Allgemeinerer Fall Risikoscheu l Streng konkave Nutzenfunktion U l U’(w) > 0; U’’(w) < 0 l Programmplanung als nichtlineares Optimierungsproblem l Bedeutung des erwarteten spezifischen DB nimmt ab l Es kommt zu Diversifikationseffekten l Maximierung des Erwartungsnutzens führt zu optimalem Produktprogramm-Portefeuille 5. 49

Beispiel Produkt DB Stunden/St 1 je zu 50% 10 oder 20 5 2 14 5 Kapazität: 1. 400 Stunden Nutzenfunktion logarithmisch; w > 0 n Annahmen: w 0 = 0 und Fixkosten = 0 Kuhn/Tucker-Bedingungen 5. 50

Beispiel. . . n Frage: Sind beide Produkte im optimalen Programm? Wird nur Produkt 1 gefertigt, darf an Stelle (280, 0) die Ableitung von LG nach x 2 nicht positiv sein Setzt man diesen Wert für l in die obige Ableitung ein, ergibt sich eine positive Differenz von 0, 00035 ðProdukt 2 ist Bestandteil des optimalen Produktionsprogramms Ähnliche Vorgehensweise zeigt, dass auch Produkt 1 im optimalen Produktionsprogramm enthalten ist 5. 51

Beispiel. . . Ermittlung des optimalen Produktionsprogramms n n Restriktion als Gleichung nach Produkt 2 auflösen Nullsetzen der 1. Ableitung 5. 52

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (4) n Entscheidungsrelevanz von Fixkosten und Anfangsvermögen abhängig von Risikoscheu n Maß der Risikoscheu Absolute Risikoaversion AR(w) Beispiel: Logarithmische Nutzenfunktion l Absolute Risikoaversion nimmt - gegeben ein Anfangsvermögen - ab l Höhere Fixkosten induzieren niedrigeres Endvermögensniveau l Wahrscheinlichkeitsverteilung für Produktionsprogramm wird in einen Bereich der Nutzenfunktion mit stärkerer Risikoscheu verschoben 5. 53

Beispiel. . . n Positives Anfangsvermögen w 0 positive, sichere Fixkosten KF n Zielfunktion Fixkosten über 3. 920 + w 0: nur Produkt 2 Anfangsvermögen über 2. 800 + KF: nur Produkt 1 5. 54

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (5) n Spezialfall Konstante absolute Risikoaversion l (sichere) Fixkosten und sicheres Anfangsvermögen wieder bedeutungslos Beispiel: exponentielle Nutzenfunktion Wegen U(d) < 0 ist -a. U(d) positiv Mit d = w 0 - KF wird Irrelevanz von KF und Anfangsvermögen deutlich 5. 55

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (6) n Stochastische Fixkosten l Potentielle Relevanz der Fixkosten wird verstärkt l Zusätzliche Diversifikationsaspekte hinsichtlich risikobehafteter Fixkosten l Auch bei konstanter absoluter Risikoaversion grundsätzliche Relevanz der Fixkosten Exponentielle Nutzenfunktion mit 5. 56

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (7) n n Keine Fixkostenrelevanz nur dann, wenn Fixkosten mit DB völlig unkorreliert sind Stochastische Fixkosten alleine induzieren keine Fixkostenrelevanz l Deckungsbeiträge dann sicher ð Zustandsabhängiges Endvermögen für jeden Zustand maximal bei Programm mit maximalem Deckungsbeitrag ð Dominanzprinzip Man kann sich auf die bekannten Sicherheitsansätze beschränken, falls die Fixkosten die alleinige risikobehaftete Größe sind 5. 57

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (8) Zusammenfassung Relevanz von Fixkosten l Fixkosten sind Ø irrelevant, falls Nutzenfunktion mit konstanter absoluter Risikoaversion und Fixkosten sicher Ø irrelevant, falls Fixkosten die alleinige stochastische Größe Ø regelmäßig auch als sichere Größe relevant, falls Nutzenfunktion ohne konstante absolute Risikoaversion Ø grundsätzlich relevant, falls neben Deckungsbeiträgen auch Fixkosten risikobehaftet und keine lineare Nutzenfunktion (Risikoneutralität) l Relevanz des Anfangsvermögens obige Ergebnisse gelten analog Ø Anfangsvermögen am Periodenbeginn aber sicher -insofern muss diesbezüglich keine Unsicherheit beachtet werden 5. 58 Ø

Nicht börsennotierte Unternehmen ohne Portefeuillewahl (9) Implikationen n Begründung der Verwendung von Vollkostenrechnungen l Streng genommen nur Vollkostenrechnungen als Periodenrechnungen n Fixkosten relevant wegen Einflusses auf Bewertung der Gewinnverteilungen l Fixkosten nach wie vor unabhängig von den Entscheidungsvariablen n Faktisch nichtlineares Entscheidungsproblem l Risikobehaftetes Endvermögen ist das Argument einer Nutzenfunktion, deren Erwartungswert zu maximieren ist n Problem: Bestimmung der Nutzenfunktion l Kurzfristig wirksames Entscheidungsproblem, das in einen längerfristigen Zusammenhang eingebettet ist l Was ist der Nutzen des Endvermögens der betrachteten Periode? Probleme mit Ausschüttungen, Effekte von Folgeentscheidungen, Bewertungsinterdependenzen 5. 59

Nicht börsennotierte Unternehmen mit Portefeuillewahl (1) n Bisherige Annahmen l Überschüsse des Programms als Grundlage für die Einkommenserzielung l Gestaltung des Produktionsprogramms muss bei unsicheren Erwartungen auch Risikoaspekte berücksichtigen l Höhe und Risiko des Einkommens bzw Endvermögens unauflöslich mit der Programmplanung verknüpft n Aber: Portefeuille aus vielfältigen Finanztiteln zusammenstellbar l Produktionsprogramm kann von Aufgaben “entlastet” werden l Unternehmung maximiert virtuellen Marktwert 5. 60

Nicht börsennotierte Unternehmen mit Portefeuillewahl (2) n Virtuelle Marktwertmaximierung l Notwendige Bedingungen: Spanning und Competitivity n Argument l Angenommen, das Unternehmen realisiert optimales Produktionsprogramm nach Erwartungsnutzenmaximierung l Dann gibt es Verbesserungsmöglichkeit wie folgt F Realisation des marktwertmaximalen Programms PM F Es gibt ein Portefeuille, welches die Überschüsse von PM dupliziert zu Gesamtpreis des Wertes von PM (Spanning) F Leerverkauf dieses Portefeuilles zum Wert von PM bei Verlust der Überschüsse aus PM F Leerverkaufserlös des Wertes von PM wird für Kauf eines Portefeuilles verwendet, das Überschüsse des ursprünglichen Programms PE dupliziert; Mittelbedarf in Höhe des Wertes von PE F Am Periodenende gleiche finanzielle Position wie vorher F Am Periodenbeginn positiver Betrag in Höhe der Wertdifferenz > 0 5. 61

Beispiel n Fortsetzung Logarithmische Nutzenfunktion 10. 000 ln(w) Fixkosten = 0 w 0 = 0 Produkt DB Stunden/St 1 je zu 50% 10 oder 20 5 2 14 5 Kapazität: 1. 400 Stunden Erwartungsnutzenmaximales Programm: 5. 62

Beispiel. . . n Überschüsse am Periodenende Bewertungsfaktoren am Kapitalmarkt Marktwertmaximales Programm: nur Produkt 1 mit 5. 63

Beispiel. . . n Am Kapitalmarkt zwei Finanztitel n = 1, 2 mit Überschüssen ün(q) Duplizierung der Überschüsse von PM mittels Stückzahlen Erwerb von 700 Stück des risikobehafteten Titels 2 Geldanlage 1. 400 0, 8 = 1. 120 zum Zinssatz von 25% Leerverkauf: Verschuldung in Höhe von 1. 120 und Leerverkauf des unsicheren Papiers im Umfang von 700 Stück Leerverkaufserlös 5. 64

Beispiel. . . n Duplizierung der Überschüsse von PE mittels Stückzahlen Erwerb von 408, 33 Stück Titel 2 Geldanlage 2. 450 × 0, 8 = 1. 960 Mittelbedarf Realisation PM + Leerverkauf Portefeuille 1 + Erwerb Portefeuille 2: Periodenende Periodenbeginn zusätzliche Mittel Sichere Investition bringt 5. 65

Nicht börsennotierte Unternehmen mit Portefeuillewahl (3) Zusammenfassung n Maximierung des virtuellen Marktwerts möglich n Fixkosten und Anfangsvermögen sind irrelevant n Anwendung eines Separationstheorems l Politik auf der Ebene der Unternehmung gemäß einer a priori bekannten Zielsetzung bestimmt unabhängig von individuellen Konsumpräferenzen 5. 66
- Slides: 66