Produktionsprogrammentscheidungen EwertWagenhofer 2014 Alle Rechte vorbehalten Ziele n

Produktionsprogrammentscheidungen © Ewert/Wagenhofer 2014. Alle Rechte vorbehalten!

Ziele n Darstellung der Lösungsverfahren für die Planung des optimalen kurzfristigen Produktionsprogramms mit und ohne Kapazitätsrestriktionen n Analyse des Einflusses von Fixkosten auf die optimale Entscheidung n Verstehen des Inhalts und des Nutzens von verschiedenen Opportunitätskosten-Konzepten 3. 2

Das Szenario Kurzfristig wirksame Entscheidungssituation n Gegebener Bestand an Potentialfaktoren n Keine zeitlichen Interdependenzen im Erlös-, Kosten- und Restriktionsbereich n Nur monetäre Zielgrößen n Ausschluss von Lagerhaltung n Sichere Erwartungen Fragestellung Welche Produkte sollen in welchen Mengen mit welchen der vorhandenen Fertigungsverfahren hergestellt und abgesetzt werden? 3. 3

Vollkosten oder Teilkosten? Zerlegung des Gesamtproblems nach der Fristigkeit Verwendung nur variabler Komponenten ist hinreichend (nicht notwendig) Fehlerpotential dann, wenn als reine Stückrechnung durchgeführt 3. 4

Grafische Verdeutlichung 3. 5

Restriktionstypen n Inhaltliche Ausrichtung l Beschaffung l Produktion l Absatz (etc. ) n Gleichungen oder Ungleichungen n Grundsätzlich auch in nichtlinearer Form möglich n Wichtige Differenzierung nach der Wirksamkeit von l Einproduktrestriktionen l Mehrproduktrestriktionen 3. 6

“Reine” Programmplanung auf Basis der einstufigen DB-Rechnung Gegebene Verfahren bei technisch unverbundenen Prozessen Unter den Nebenbedingungen 3. 7

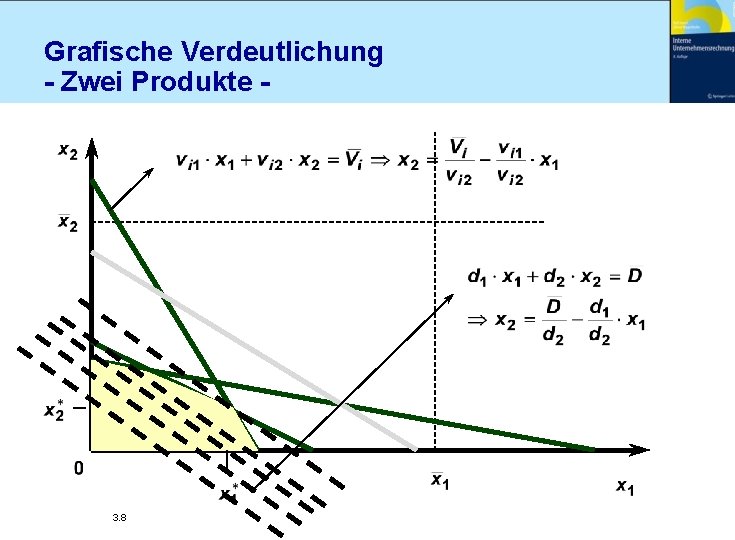
Grafische Verdeutlichung - Zwei Produkte - 3. 8

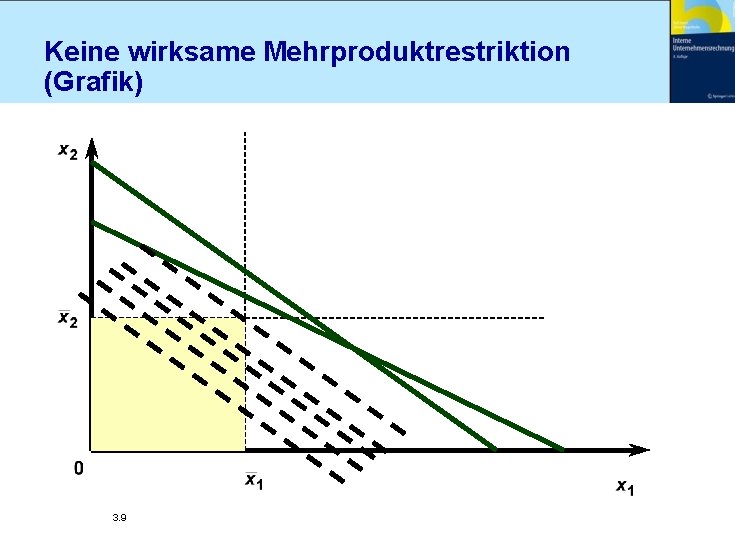
Keine wirksame Mehrproduktrestriktion (Grafik) 3. 9

Keine wirksame Mehrproduktrestriktion (Procedere) Identifizierung aller Produkte mit dj > 0 n Die jeweiligen Mengen werden auf die zugehörigen Absatzobergrenzen gesetzt n Falls keine Mehrproduktrestriktion bindet, hat man das optimale Programm gefunden n “Ausgangslösung” 3. 10

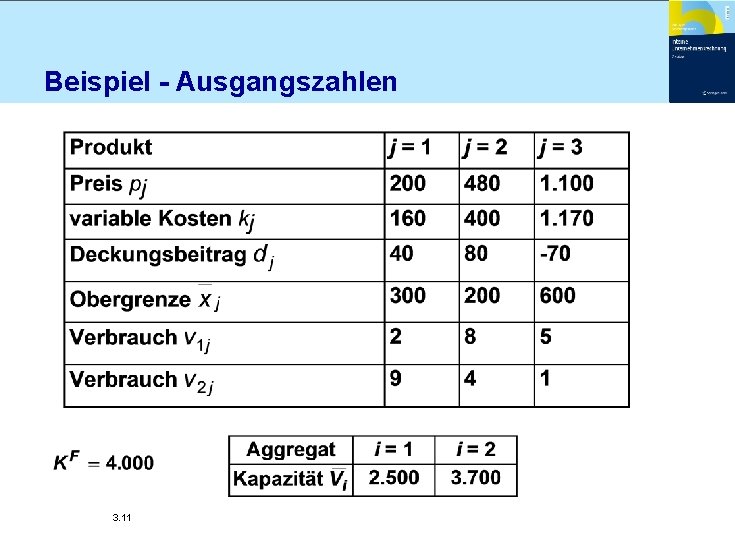
Beispiel - Ausgangszahlen 3. 11

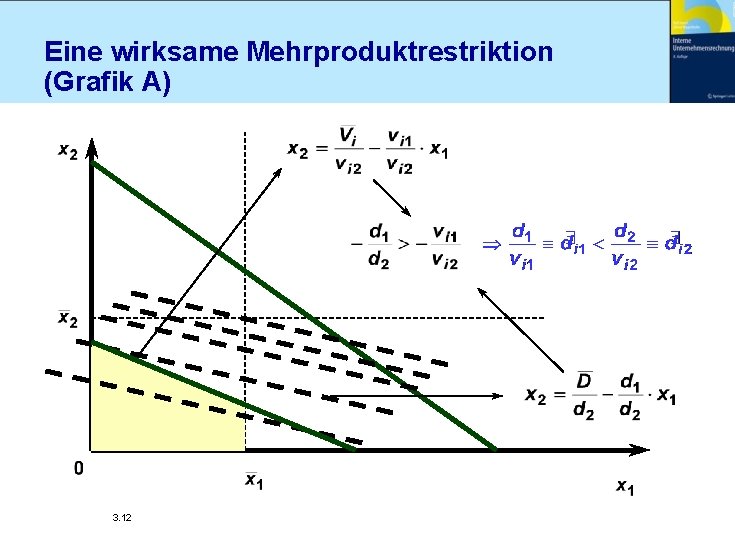
Eine wirksame Mehrproduktrestriktion (Grafik A) 3. 12

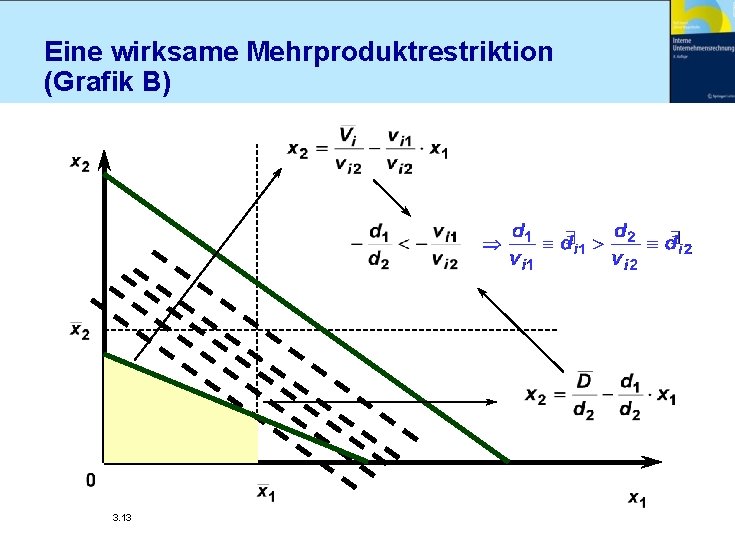
Eine wirksame Mehrproduktrestriktion (Grafik B) 3. 13

Eine wirksame Mehrproduktrestriktion (Grundsätzliches Procedere) 3. 14

Eine wirksame Mehrproduktrestriktion Beispiel - 3. 15

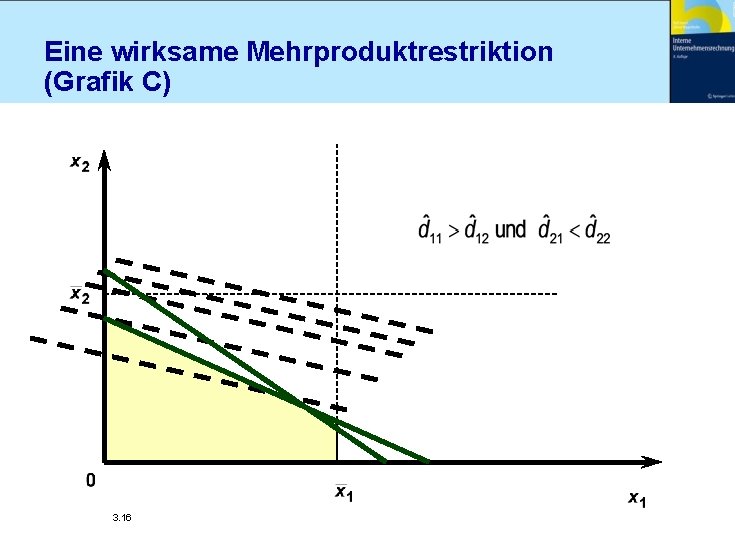
Eine wirksame Mehrproduktrestriktion (Grafik C) 3. 16

Eine wirksame Mehrproduktrestriktion Spezialfälle n Grundsätzliche Regel kann beibehalten werden, wenn l wenigstens zwei Mehrproduktrestriktionen bei Ausgangspolitik binden und l die Rangfolge der Produkte gemäß spezifischer Deckungsbeiträge für all diese Restriktionen gleich ist l es eine für alle Produkte gleichmäßig strengste Mehrproduktrestriktion gibt 3. 17

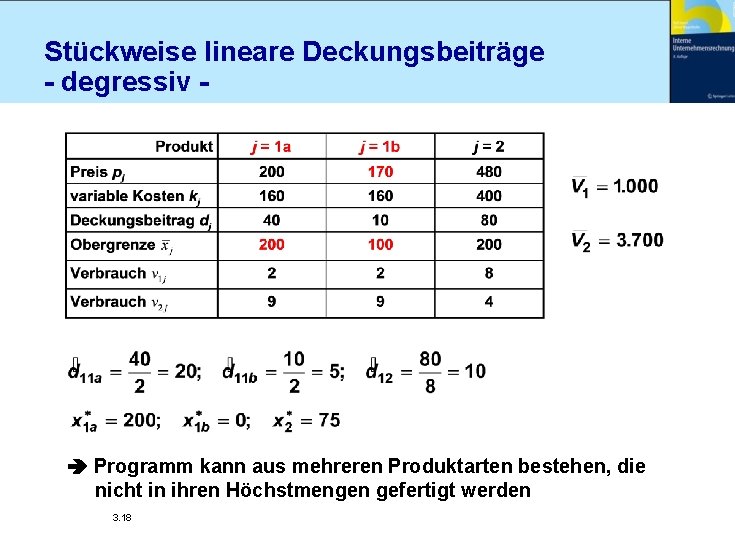
Stückweise lineare Deckungsbeiträge - degressiv - Programm kann aus mehreren Produktarten bestehen, die nicht in ihren Höchstmengen gefertigt werden 3. 18

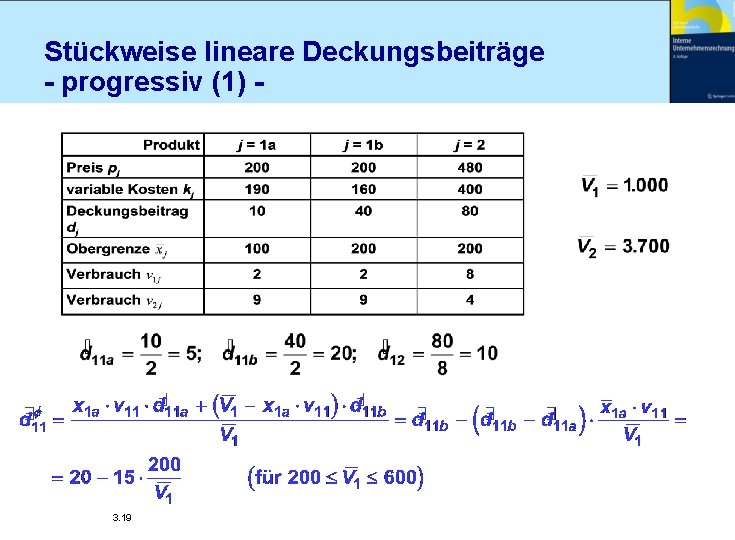
Stückweise lineare Deckungsbeiträge - progressiv (1) - 3. 19

Stückweise lineare Deckungsbeiträge - progressiv (2) n Je mehr Kapazität vorhanden, desto günstiger wird im Durchschnitt Produktart 1 n “Kritischer” Mittelvorrat 3. 20

Mehrere wirksame Mehrproduktrestriktionen 3. 21

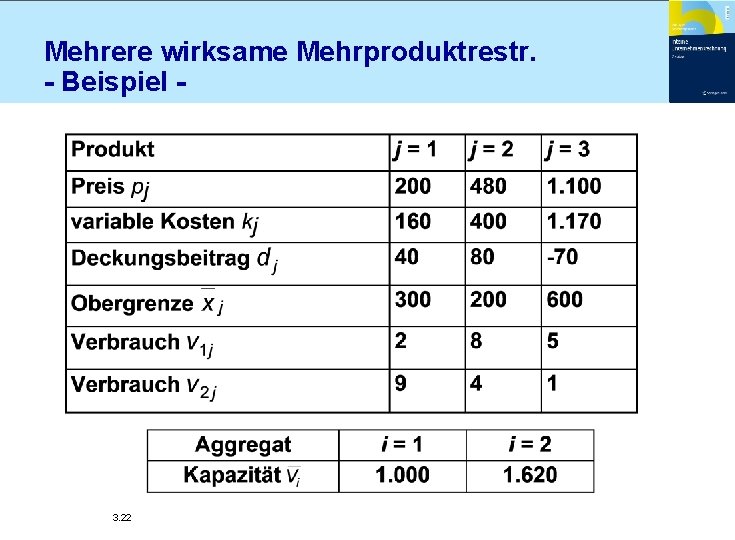
Mehrere wirksame Mehrproduktrestr. - Beispiel - 3. 22

Gleichungssystem 3. 23

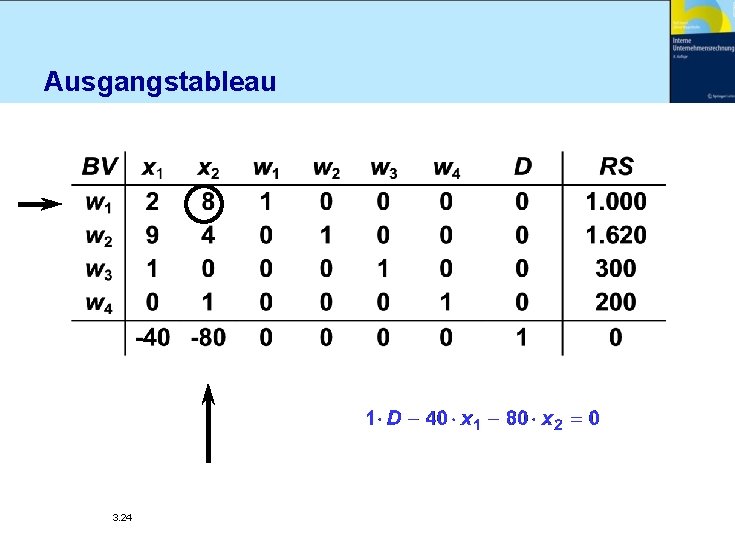
Ausgangstableau 3. 24

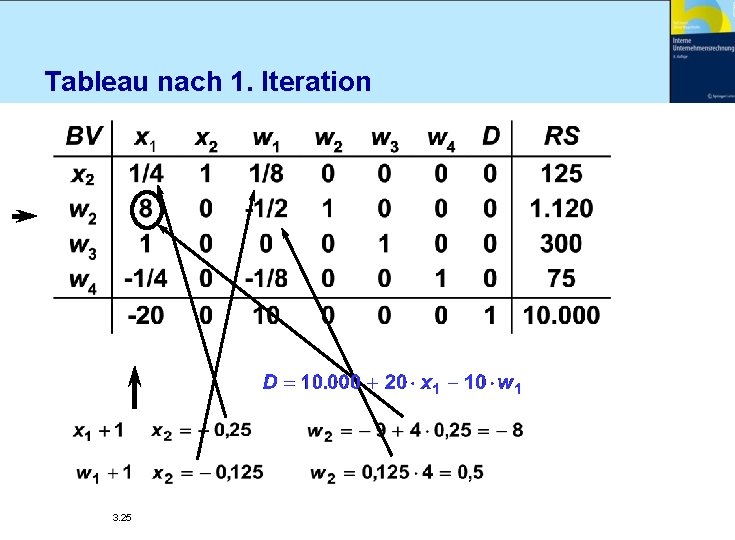
Tableau nach 1. Iteration 3. 25

Tableau nach der 2. Iteration (Endtableau) 3. 26

Sensitivität und Endtableau - Ceteris Paribus - 3. 27

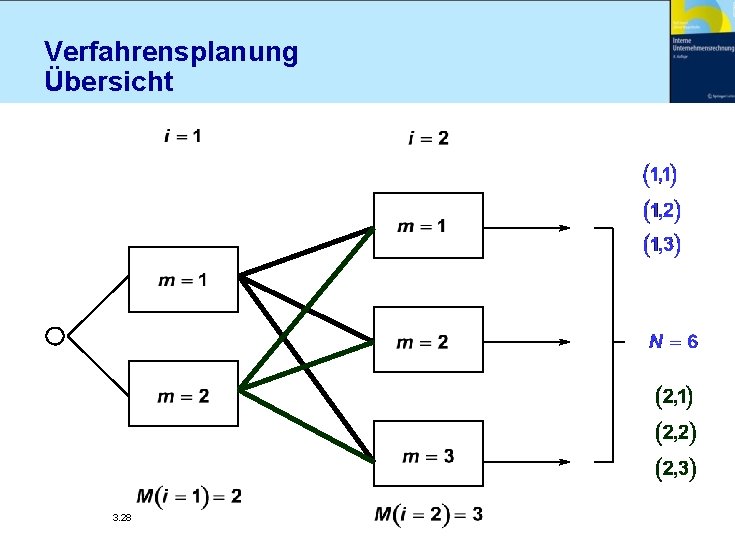
Verfahrensplanung Übersicht 3. 28

Alternativkalkulation 3. 29

Alternativkalkulation versus Arbeitsgangverfahren Alternativkalkulation n Vorteile l Adaption des Standardverfahrens l Daher standardmäßig lösbar n Nachteile l Viele Kombinationen (multiplikativ) l Viele Kalkulationen l Daher relativ teuer 3. 30 n Vorteile l “Direkte” Planung der Verfahren l Relativ wenig Variablen (additiv) l Daher relativ günstiger n Nachteile l Neue Restriktionstypen l Daher nicht mehr standardmäßig lösbar

Arten von Opportunitätskosten Inputbezogen l Bei optimalem Einsatz des Faktors erzielbarer Grenzerfolg/Faktoreinheit n Outputbezogen/Optimal l Ressourcenbewertung mit inputbezogenem Grenzerfolg n Outputbezogen/Alternativ l Ressourcenbewertung mit Erfolg der besten, nicht mehr genutzten Verwendung 3. 31

Intention der Verwendung von Opportunitätskosten n Ressourcen können knapp sein n Einbeziehung der Knappheit in den Wertansatz von Ressourcen n Neue Kostenbewertung von Ressourcenverwendungen, wie bspw. Produkte, etc. n Dadurch modifzierte Rangfolge der Vorteilhaftigkeit von Verwendungen n Optimum könnte sich ggf alleine daraus schon bestimmen lassen n Dann benötigte man kein umfassendes Modell unter expliziter Einbeziehung sämtlicher Restriktionen 3. 32

Inputbezogene Opportunitätkosten - Formale Zusammenhänge (1) - 3. 33

Inputbezogene Opportunitätskosten - Formale Zusammenhänge (2) - 3. 34

Outputbezogene Optimalkosten 3. 35

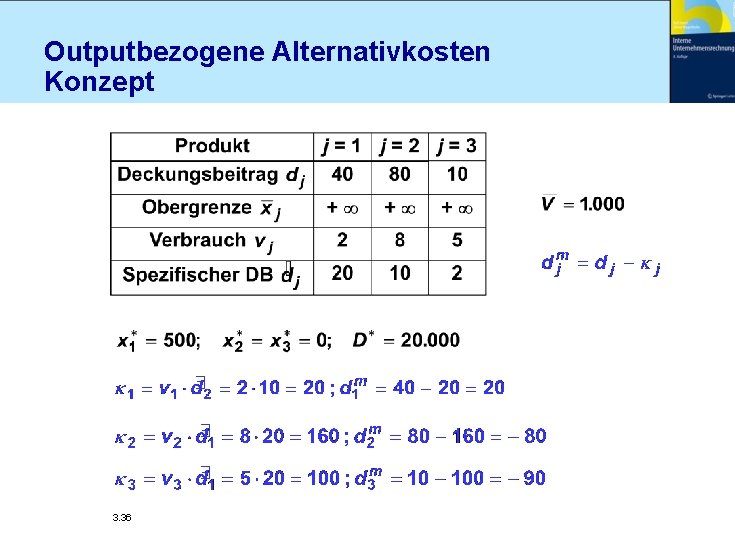
Outputbezogene Alternativkosten Konzept 3. 36

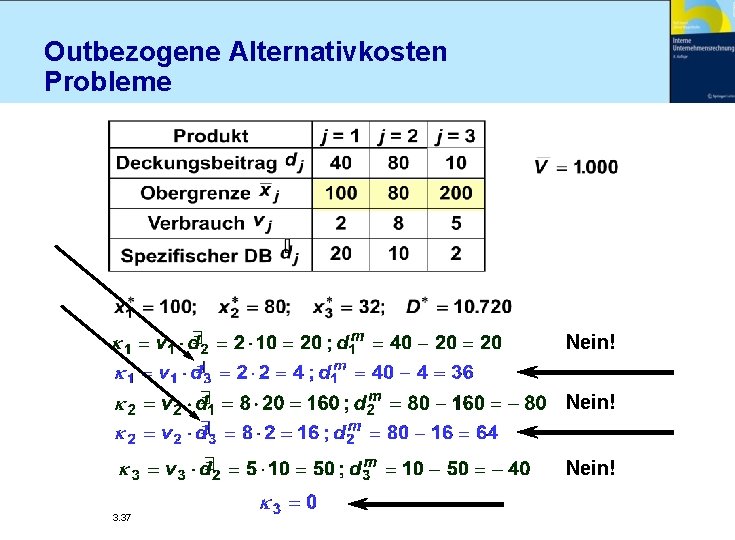
Outbezogene Alternativkosten Probleme Nein! 3. 37

Opportunitätskosten Beurteilung n Es gibt Größen mit der Eigenschaft, dass Knappheit in den Wertansatz integriert ist n Eine richtige Ermittlung setzt aber die Kenntnis der Lösung voraus (auch bei Alternativkosten) n Im linearen Fall könnte auch dann nicht auf ein explizites und umfassendes Modell verzichtet werden n Angedachte Vorteile so nicht existent n Verwendungsmöglichkeiten im Rahmen von postoptimalen Analysen n Beispiel dafür: Preisuntergrenzen von Zusatzaufträgen, etc. 3. 38

Nichtlineare Ansätze Besonderheiten Optimum muss keine Randlösung sein n Eine wirksame Mehrproduktrestriktion n l Rangfolge gemäß spezifischer Grenzdeckungsbeiträge l Diese SGD sind aber variabel l Zuordnung daher unter Berücksichtigung sowohl der Ø Absatzobergrenzen, als auch der Ø SGD nachfolgender Produkte l Ggf. werden mehrere Produkte parallel zugerodnet n Undifferenzierte Anwendung der Lagrange-Methode führt nicht immer zur korrekten Lösung 3. 39