The History of Mathematics Early Greek Michael Flicker

The History of Mathematics Early Greek Michael Flicker OLLI Spring 2018 1

Early Greek History (Morris Kline) • The Greek civilization dates back to ~ 2800 BCE • Settled in Turkey, Greece, southern Italy, Sicily, Crete, Rhodes, Delos, and North Africa • ~ 800 BCE replaced various hieroglyphic systems of writing with Phoenician alphabet • With the adoption of an alphabet the Greeks became more literate and more capable of recording their history and ideas. • Greeks visited and traded with the Egyptians and Babylonians • Went to Egypt to travel and study • Visited Babylonia and learned mathematics and science there • Miletus – birthplace of Greek philosophy, math, and science 2

Greek/Hellenistic Timeline • Classical Period (500 -336 BC) - Classical period of ancient Greek history, is fixed between about 500 B. C. , when the Greeks began to come into conflict with the kingdom of Persia to the east, and the death of the Macedonian king and conqueror Alexander the Great in 323 B. C. In this period Athens reached its greatest political and cultural heights: the full development of the democratic system of government under the Athenian statesman Pericles; the building of the Parthenon on the Acropolis; the creation of the tragedies of Sophocles, Aeschylus and Euripides; and the founding of the philosophical schools of Socrates and Plato. • Hellenistic Period (336 -146 BC) - period between the conquest of the Persian Empire by Alexander the Great and the establishment of Roman supremacy, in which Greek culture and learning were pre -eminent in the Mediterranean and Asia Minor. It is called Hellenistic (Greek, Hellas, "Greece") to distinguish it from the Hellenic culture of classical Greece. 3

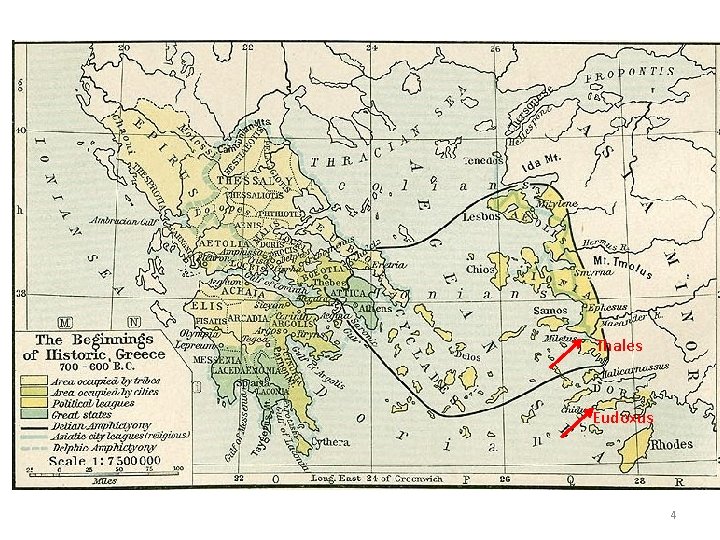
Thales Eudoxus 4

5

Early Greek Number System • Acrophonic Attic ~ 600 BC to ~ 300 BC Similar to Roman Numerals Denotes drachma 6

Later Greek Number System • Ionic (Alphabetical) ‘εχοη = 5678 7

Fractions • Acrophonic – With the exception of monetary amounts, there were no acrophonic numerals for fractions • Ionic – Used apostrophe to signify fraction ’ = 1/32 • Addition, subtraction, multiplication and division 8

Early Greek Mathematics Roughly 600 BC to 300 AD 9

How do we know about Greek mathematics? • Initially knowledge was passed from teacher to student orally • Probably around 450 BCE chalk boards and wax tablets were introduced for non permanent work. • Papyrus rolls were used for permanent records but new copies were required frequently. • In about 300 BCE Euclid’s Elements was completed and it was so comprehensive and of such quality that all older mathematical texts became obsolete. • In 2 nd century CE books of papyrus appeared and became the main form in the 4 th century. Also vellum (animal skin) was introduced. 10

How do we know about Greek mathematics? • If the person copying the “Elements” was a mathematician, material not in the original text may have been added • The oldest surviving complete copy of the Elements is from 888 CE probably based on a version with commentary and additions produced by Theon of Alexandria in the 4 th century CE • In addition to the 888 AD document there are numerous fragments some dating to as early as 225 BCE • Some surviving texts exist that were written after 888 CE that were based on versions of the elements earlier than 888 CE • First print edition in Venice in 1482 • For the complete story see the article “How do we know about Greek mathematics” on the Mac Tutor History of Mathematics 11

Major Schools of the Classical Period • Miletus School – founded by Thales (c 640 – c 546 BCE) – Anaximander, Anaximenes, and Pythagoras students of Thales – Anaxagoras belonged to this school then moved to Athens • Pythagoras formed his own large school in southern Italy • Xenophanes of Colophon in Ionia migrated to Sicily in southern Italy and founded a center (view contested) – Parmenides and Zeno belonged – School moved to southern Elea in Italy and became the Eleatic school • • Sophists active from latter half 5 th century in Athens Academy of Plato in Athens – Aristotle student School of Eudoxus School of Aristotle 12

Greek Mathematics – Thales of Miletus • Thales of Miletus 624 BC – 547 BC (Ionia) – – – None of his writings survive (if there were any) Name appears in the writings of others years later The first of the seven sages of antiquity A pupil of the Egyptians Credited by Proclus with five theorems of elementary geometry • A circle is bisected by any diameter • The angles between two intersecting straight lines are equal • Two triangles are congruent if they have two angles and a corresponding side equal • The base angles of an isosceles triangle are equal • An angle in a semicircle is a right angle 13

More on Thales • The development of geometry is preserved in a work of Proclus (412 – 485 CE), A Commentary on the First Book of Euclid’s Elements. Proclus provided a remarkable amount of intriguing information, the vital points of which are the following: Geometry originated in Egypt where it developed out of necessity; it was adopted by Thales who had visited Egypt, and was introduced into Greece by him • The Commentary of Proclus indicates that he had access to the work of Euclid and also to The History of Geometry (now lost) which was written by Eudemus of Rhodes, a pupil of Aristotle. His wording makes it clear that he was familiar with the views of those writers who had earlier written about the origin of geometry. He affirmed the earlier views that the rudiments of geometry developed in Egypt because of the need to re-define the boundaries. 14

Greek Mathematics – Pythagoras of Samos • Pythagoras (585 BCE – 497 BCE) • Founded a religious, scientific, and philosophical brotherhood in Croton in southern Italy • It was a formal school with limited membership – teachings were kept secret • The Pythagoreans got on the wrong side of local politics and had to flee. • There are no written works by the Pythagoreans – We know about them through the writings of others including Plato and Herodotus 15

All is Number • One of the scientific achievements of Pythagoras was the discovery of the mathematical order in the musical scale and the harmonies so produced. It is believed that he experimented with string instruments and discovered that two tones sound well together when the ratios of their frequencies can be expressed by the use of small numbers and the smaller the numbers the better is the harmony. 20 22/12 24/12 25/12 27/12 29/12 211/12 212/12 Table from “Science & Music” by Sir James Jeans 16

All is Number • Boethius (~ 500 CE) tells us that Pythagoras investigated the relation between the length of a vibrating string and the musical tone it produced. If a string was shortened to ¾ of its original length, then what is called the fourth of the original tone was heard; if shortened to 2/3, the fifth was heard; and if shortened to 1/2 , the octave. The string lengths were proportional to 12, 9, 8, and 6. • The Pythagorean school was able to find many interesting relations between these number including the fact that a cube has 6 faces, 8 vertices, and 12 edges. They were able to convince themselves that since these combinations of string lengths produced sounds that harmonize, the numbers themselves essentially caused it. The Pythagoreans extrapolated that the natural numbers are fundamental to natural science. • This was bad science but really good for number theory 17

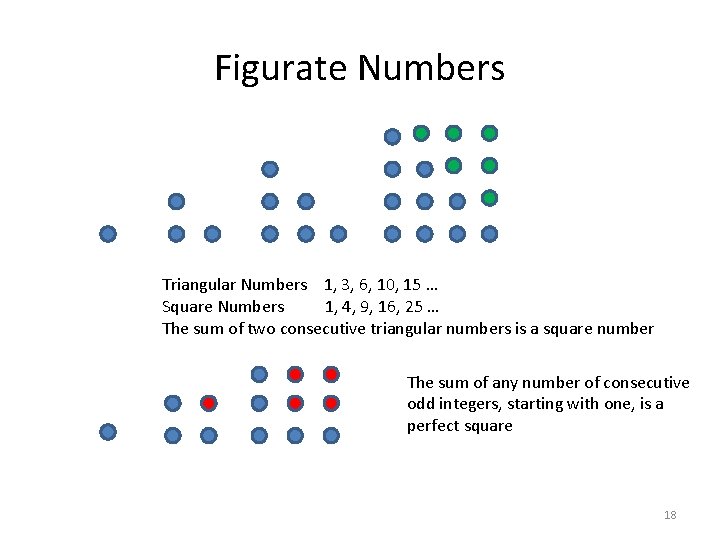
Figurate Numbers Triangular Numbers 1, 3, 6, 10, 15 … Square Numbers 1, 4, 9, 16, 25 … The sum of two consecutive triangular numbers is a square number The sum of any number of consecutive odd integers, starting with one, is a perfect square 18

Pythagorean “Arithmetica” • Pythagorean triplets – natural numbers that satisfy • Pythagoreans knew that when m is odd, then a = m, b = (m 2 – 1)/2, and c = (m 2 + 1)/2 are such a triplet. For example for m = 3, the triplet is 3, 4, 5. However the formula does not produce all triplets. • Euclid solves the general problem is his Elements. • a = 2 mn, b = m 2 – n 2, c = m 2 + n 2 • Choose m = 75 and n = 32, a = 4800, b = 4601, c = 6649 • One of the sets in Plimpton 322 19

More “Arithmetica” • Perfect numbers – the number is the sum of its divisors. 6=1+2+3 28 = 1 + 2 + 4 + 7 + 14 496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 8128 33550336 The search for perfect numbers continues to today. No odd perfect numbers have been found. • Friendly numbers – pairs of numbers such that each is the sum of the divisors of the other – The first friendly pair is 220 & 284 The secondly pair is 17, 296 and 18, 416 and was independently discovered by al-Banna (Arab 1256 – 1321) and by Fermat in 1636 In the 1970 s the phrase “friendly numbers” started to be used differently 20

Still More “Arithmetica” • The Pythagoreans studied prime numbers, progressions, and ratios and proportions. They understood that certain sums could be easily calculated. 1 + 2 + … + n = (n/2)(n + 1) • Numbers to Pythagoreans were whole numbers only. The ratio of two whole numbers was not a fraction and therefore another kind of number. Actual fractions were employed in commerce. • Arithmetica included the understanding of even and odd numbers – The sum of two even numbers is even – The product of two odd numbers is odd – When an odd number divides an even number, it also divides its half 21

Pythagorean School Geometry • In the 5 th century BCE geometry, theorem/proof logic took root and a system of theorems was developed where theorems were proved based on theorems previously proved. • Studied triangles, parallel lines, polygons, circles, spheres and regular polyhedra • Worked on a class of problems known as “application of area” – Example – Construct a polygon equal in area to a given one and similar in shape to another given one. – Squaring the circle 22

Pythagorean School Geometry • Did the Pythagoreans prove their geometric results? • During most of the life of the school the members probably affirmed results on the basis of special cases. By 400 BCE they may have given some real proofs • Did they prove the Pythagorean Theorem? Proclus credits the proof to Euclid so the Pythagoreans probably did not have a real proof. 23

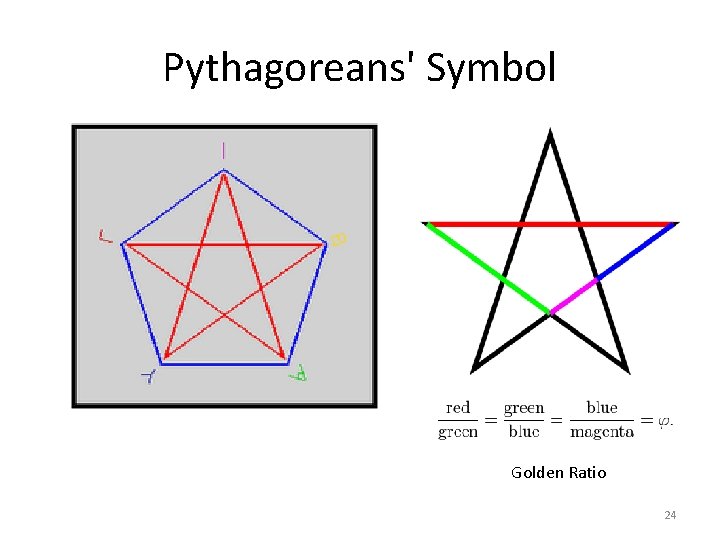
Pythagoreans' Symbol Golden Ratio 24

Golden ratio and Golden Rectangle 25

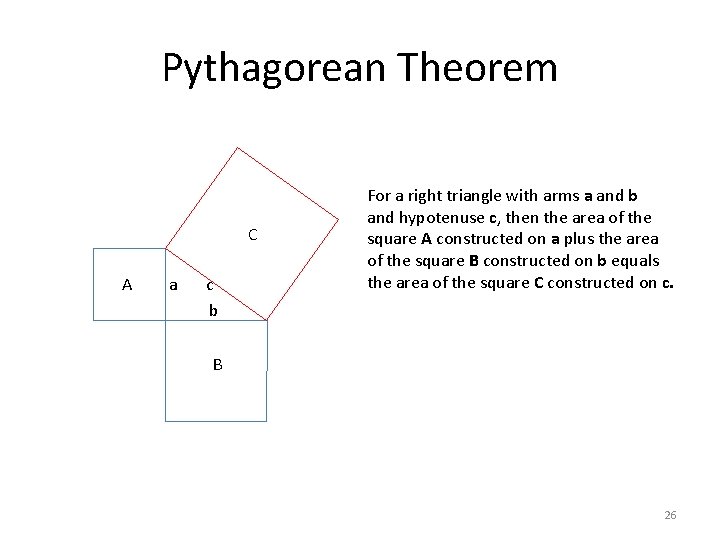
Pythagorean Theorem C A a c b For a right triangle with arms a and b and hypotenuse c, then the area of the square A constructed on a plus the area of the square B constructed on b equals the area of the square C constructed on c. B 26

Proof of Pythagorean Theorem The areas of the two large squares are equal. The area of the square on the left is 4 triangles + square A + square B. The area of the square on the right is 4 triangles + square C. Since all eight triangles are identical, The area of A + the area of B = the area of C 27

Rational Numbers • The concept of integers comes from counting objects • Life requires us to measure quantities such as length, speed, weight, time , … • To satisfy these measurements fractions (ratios) are required. No matter how accurately it is necessary to measure something, that measurement can always be expressed as a fraction of the unit of measure. • Early mathematicians thought of numbers as points on a line and believed that all points could be expressed as fractions. 28

Irrational Numbers • From the Pythagorean theorem it follows that for a square with its side equal to 1 the hypotenuse equals. The Pythagoreans tried to find two natural numbers whose ratio was , but failed. • The discovery of “irrational” ratios is attributed to Hippasus of Metapontum (5 th cent. B. C. ) • After the was revealed to be irrational, the Pythagoreans, according to a legend, killed Hippasus, not willing to believe this fundamental number could fail to be a ratio of integers. 29

• Proof that is irrational – a/b = where both a and b are integers and the ratio a/b has been reduced to lowest terms. This means that a and b cannot both be even. – a 2 = 2 b 2 – a must be even since if it were odd then a 2 would be odd. – If a is even it can be written as 2 c implying 4 c 2 = 2 b 2 or 2 c 2 = b 2 – By the same argument as above b must be even. – The assumption that is rational leads to a contradiction. • Was the first irrational number? 30

Platonic Solids http: //www. 3 quarks. com/en/Platonic. Solids/index. html Pythagoras – Tetrahedron – 4 equilateral triangles – Cube (hexahedron) – 6 squares – Dodecahedron – 12 equilateral pentagons • Theaetetus (417 BC – 369 BC) – Octahedron – 8 equilateral triangles – Icosahedron – 20 equilateral triangles • In book XIII of Euclid’s elements it is shown that there are only five convex regular polyhedra • So why are these called the Platonic solids? 31

Platonic solids 32

The Eleatic School • Zeno, born c. 490 BCE, was a member of the Eleatic school, and most of what we know personally about him is from Plato's dialogue Parmenides. • In defense of Parmenides’ views on the relation of the discrete to the continuous, Zeno proposed a number of paradoxes of which four deal with motion. • The first view was that space and time are infinitely divisible, in which case motion is continuous and smooth; and the second that space and time are made up of indivisible small intervals, in which case motion is a succession of small jerks 33

More Zeno • The second paradox is called the Achilles and the Tortoise and addresses the view that space and time are infinitely divisible. • Achilles and the tortoise decide to have a race. Achilles is known to be the faster runner of the two, and therefore decides to give the tortoise a head start. Once the race begins, it is true to say that Achilles will take some time to reach the starting point of the tortoise. During this finite time, it is also true to say that the tortoise will have moved forward by some finite distance, and will therefore still maintain a lead in the race. Achilles will once again take some time to reach the tortoise's new position, during which the tortoise will move forward some distance yet again, thus maintaining his lead. • This continues on forever. Therefore Achilles never overtakes the tortoise. 34

The Sophist School • After the defeat of the Persians by the Greeks at Mycale in 479 BCE, Athens became the major city in ancient Greece. • The first Athenian school was the Sophist school and one of their chief pursuits was the use of mathematics to understand the functioning of the universe. • Many of the mathematical results obtained were by-products of their efforts to solve three famous construction problems. 35

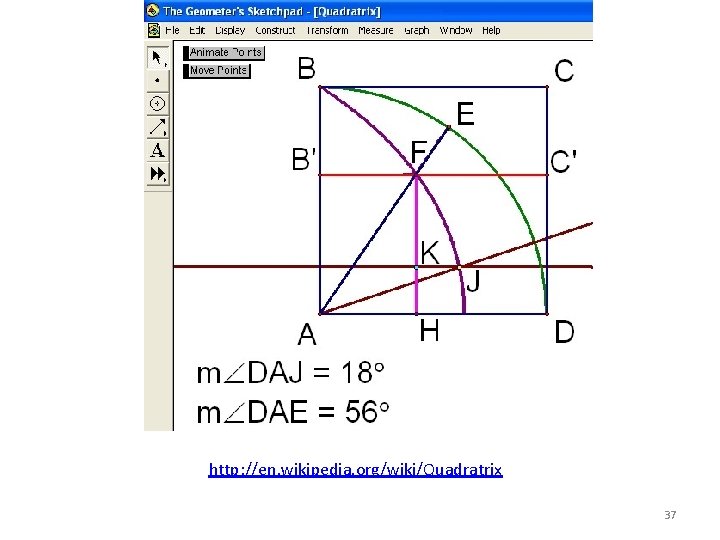
The Three Famous Geometry Problems of Antiquity • These three problems were to be solved using a straight edge (not a ruler) and compass – Squaring the circle (Anaxagoras, 500 BC – 428 BC worked on problem while in prison) – Doubling the cube (worked on by Hippocrates of Chios, 470 BC – 410 BC, Sophist). Hippocrates is credited with the idea of arranging theorems so that the later ones can be proven on the basis of the earlier ones. – Trisecting an angle (worked on by Hippias of Elis, born c 460 BCE, a leading Sophist). Hippias invented the quadratrix 36

http: //en. wikipedia. org/wiki/Quadratrix 37

Lune of Hippocrates C E F A D B The area of the semicircle ACE equals the area of the quarter circle ADC. Hence the area of the lune ACEF equals the area of triangle ADC The fact that a shape that appears to be related to a circle can be shown to be equal in area to a triangle led folks to believe that the circle could be squared. Hippocrates of Chios was the most famous mathematician of his century. A contemporary, Hippocrates of Cos (460 BC – 375 BC), is the father of medicine 38

Famous Problems • Squaring the circle – Squaring the circle involves constructing the square root of π which was shown to be impossible in 1882 when Ferdinand von Lindemann proved that π is transcendental. • Doubling the cube (Delian problem) & trisecting an angle – Both these problems require finding the cube root of a quantity. In 1837 Pierre Wantzel showed the problems are unsolvable by compass and straightedge construction. – There are certain angles that can be trisected, e. g. , 90 degrees but in general it cannot be done. 39

Beginning of the “Elements” • Hippocrates of Chios – wrote the first Elements around 430 BC. – After Hippocrates at least four other Elements were written each improving on the previous versions – Euclid wrote his Elements in about 300 BC 40

The Platonic School • Theodorus of Cyrene (born c. 470 BCE) and Archytas of Tarentum (428 – 347 BCE) were both Pythagoreans and both taught Plato. • Theodorus is noted for having proved that the square roots of the non-square numbers up to 17 are irrational. • Archytas introduced the idea that a curve is generated by a moving point and a surface by a moving curve. He also provided a solution of the duplication of a cube problem. • Plato founded his Academy in Athens about 387 BCE. 41

Plato and Mathematics • Plato was not a mathematician but his enthusiasm for the subject and his belief in its importance for philosophy and the understanding of the universe encouraged mathematicians to pursue it. • Almost all the important mathematical work of the fourth century was done by friends and pupils of Plato • Plato himself seems to have been more concerned to improve and perfect what was known. • It appears that starting with Plato’s school concepts of mathematics became abstract. • Numbers and geometrical concepts were distinct from physical things. • Concepts of mathematics have a reality of their own and are discovered, not invented or fashioned. 42

Contribution of the Platonic School • Deduction – He demanded of his students accurate definitions, clearly stated assumptions, and logical deductive proof, and he insisted that geometric proofs be demonstrated with no aids other than a straight edge and a compass. • What do we do? – probable knowledge – Induction – Observation – Experimentation • Most significant discovery probably the conic sections – Attributed to Menaechmus a pupil of Eudoxus – Looked at the intersection of a plane with various shaped cones – Literature suggests it came out of work on the construction of sundials • Theaetetus generalized theory of irrationals – The square (cube) root of a whole number is rational if and only if the number is a perfect square (cube) of whole numbers. 43

Eudoxus of Cnidus (408 – 355 BC) Eudoxus did everything • Philosopher • Geometer • Astronomer – Created the first astronomical theory of the heavenly motions • Geographer • Physician • Legislator He is consider to be one of the greatest of the ancient mathematicians, second only to Archimedes 44

Eudoxus of Cnidus • Born in Cnidus in Asia Minor • Studied geometry under Archytas in Italy and medicine with Philistion in Sicily • At age 23 he went to Athens for two months to attend lectures • Traveled to Egypt for 16 months where he learned astronomy from the priests of Heliopolis and made measurements at their observatory (~ 381 – 380 BCE) • Founded school at Cyzicus in northern Asia Minor • About 368 BCE he and his followers joined Plato • Some years later he returned to Cnidus where he died in 355 BCE 45

Astronomy • • The spherical earth is at rest at the center of the universe. Around this center, 27 concentric spheres rotate. The exterior one caries the fixed stars, The others account for the sun, moon, and five planets. – Mercury, Venus, Mars, Jupiter, and Saturn • Each planet requires four spheres, the sun and moon, three each. 46

Eudoxus of Cnidus – Theory of Proportion • In modern terms: a/b = c/d if and only if, for all integers m and n, whenever ma < nb then mc < nd, and so on for > and =. • Conceptually, this is an infinite process but it was needed to deal with incommensurables. It was now possible to compare the “magnitudes” of rational and irrational ratios. • Unfortunately, the concept of magnitude was only applied to geometric concepts such as line segments, angles, areas, etc and not to numbers. Numbers were integers. • Eudoxus solved the problem of comparing incommensurables in geometry but forced a separation between number and geometry. • It took two thousand years to recover 47

Eudoxus of Cnidus – Method of Exhaustion • The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will become arbitrarily small as n becomes large. As this difference becomes arbitrarily small, the possible values for the area of the shape are systematically "exhausted" by the lower bound areas successively established by the sequence members. 48

Eudoxus of Cnidus – Method of Exhaustion • XII. 1 Similar polygons inscribed in circles are to one another as the squares on their diameters • XII. 2 Circles are to one another as the squares of their diameters • XII. 6 Pyramids of the same height with polygonal bases are to one another as their bases • XII. 7 Any pyramid is the third part of the prism with the same base and equal height • XII. 10 Any cone is the third part of the cylinder with the same base and equal height • XII. 18 Spheres are to one another in triplicate ratio of their respective diameters. 49

Eudoxus of Cnidus • Some consider him to be the greatest of the ancient mathematicians, second only to Archimedes • Resolved the difficulty in comparing rational and irrational numbers • Put the method of exhaustion on a rigorous basis – Similar to the limit concept of calculus – Proved the volume of a pyramid (cone) equals 1/3 vol. prism (cylinder) with same base and equal height – Area of circles go as the square of their diameters and the volume of spheres go as the cubes of their diameters • The first to present a general geometric model of celestial motion. 50

Aristotle (384 - 322 BCE) • A student of Plato and a tutor of Alexander the Great • Primarily a philosopher and biologist but a competent mathematician current on the activities of the mathematicians • The works of Aristotle are important particularly to Euclid’s Elements because they come just before the Elements and show the innovations in the Elements that are Euclid’s. In particular, Euclid’s formulation of the postulates and many propositions are his own. An example is the proposition that an angle inscribed in a semicircle is a right angle. Aristotle’s proof is much different than Euclid’s 51

Aristotle (384 - 322 BCE) • A major achievement of Aristotle was the founding of the science of Logic. In producing correct laws of mathematical reasoning the Greeks had laid the groundwork for Logic, but it took Aristotle to codify and systematize these laws into a separate discipline. 52

References • I have borrowed liberally from: 1) Mathematical Thought from Ancient to Modern Times, Morris Kline 3) A History of Mathematics, Carl B. Boyer 4) The Mac Tutor History of Mathematics archive, University of St Andrews Scotland 5) A History of Greek Mathematics, Sir Thomas Heath 6) Wikipedia and other web sites 7) Famous Problems of Elementary Geometry, Felix Klein 8) Science & Music by Sir James Jeans (Dover) 9) The Works of Archimedes, edited by Sir Thomas L. Heath 10) God Created the Integers – The Mathematical Breakthroughs that Changed History, Edited by Stephen Hawking 53