Rgression logistique et analyse discriminante comparaisons thoriques et







































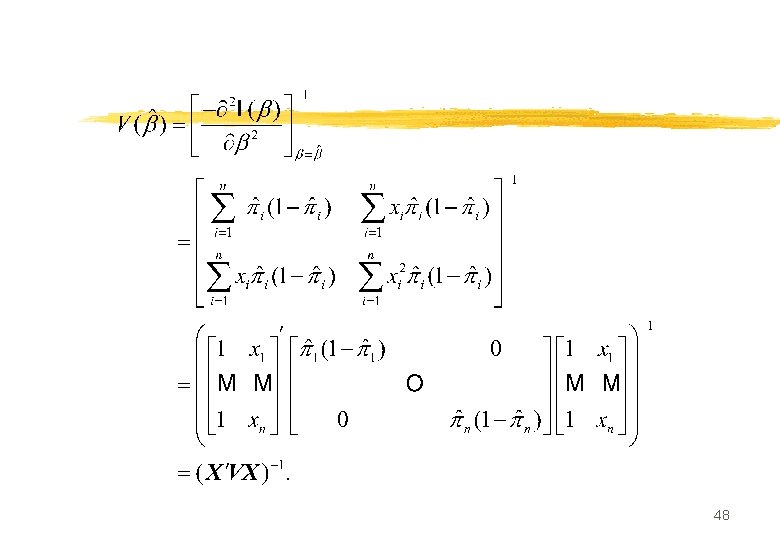

































- Slides: 95

Régression logistique et analyse discriminante : comparaisons théoriques et pratiques Gilbert Saporta Conservatoire National des Arts et Métiers saporta@cnam. fr http: //cedric. cnam. fr/~saporta 1

Bibliographie n Bardos: « Analyse discriminante » , Dunod, 2001 n Celeux, Nakache : « Analyse discriminante sur variables qualitatives» Polytechnica , 1994 n Droesbeke, Lejeune, Saporta (éditeurs): « Modèles statistiques pour données qualitatives » Technip, 2005 n Hastie, Tibshirani, Friedman : « The Elements of Statistical Learning » , Springer-Verlag, 2001 n Hosmer, Lemeshow : «Applied logistic regression» , Wiley, 2000 n Nakache, Confais: « Statistique explicative appliquée » , Technip, 2003 n Thomas, Edelman, Crook: « Credit scoring and its applications » , SIAM, 2002 2

Plan n I L’analyse discriminante n II La régression logistique n III Prédicteurs qualitatifs et scoring n IV Comparaison 3

Objet d’étude n Observations multidimensionnelles réparties en k groupes définis a priori. K=2 le plus souvent n Exemples d’application : n Pronostic des infarctus (J. P. Nakache) • 2 groupes : décès, survie (variables médicales) n Iris de Fisher : • 3 espèces : 4 variables (longueur et largeur des pétales et sépales) n Risque des demandeurs de crédit • 2 groupes : bons, mauvais (variables qualitatives) n Autres : • Publipostage, reclassement dans une typologie. 4

Quelques dates : n Analyse discriminante n Mahalanobis (crâniologie) 1927 n Fisher (biométrie) 1936 n Régression logistique n Berkson (biostatistique) n Cox n Mc Fadden (économétrie) 1944 1958 1973 5

I : L’analyse discriminante 1. - 2. Aspect géomètrique: Réduction de dimension, axes et variables discriminantes. Cas de 2 groupes. Méthodes géométriques de classement. AD probabiliste 6

Représentation des données n n points dans p appartenant à k groupes. 7

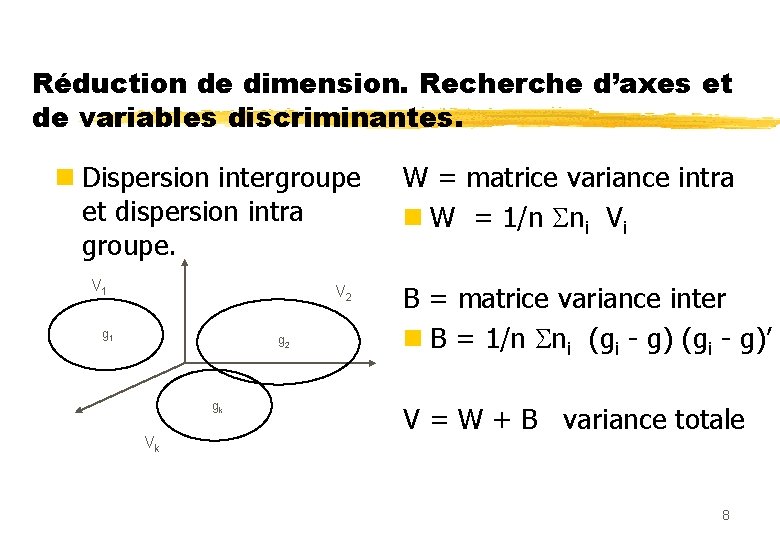
Réduction de dimension. Recherche d’axes et de variables discriminantes. n Dispersion intergroupe et dispersion intra groupe. V 1 V 2 g 1 g 2 gk Vk W = matrice variance intra n W = 1/n ni Vi B = matrice variance inter n B = 1/n ni (gi - g)’ V = W + B variance totale 8

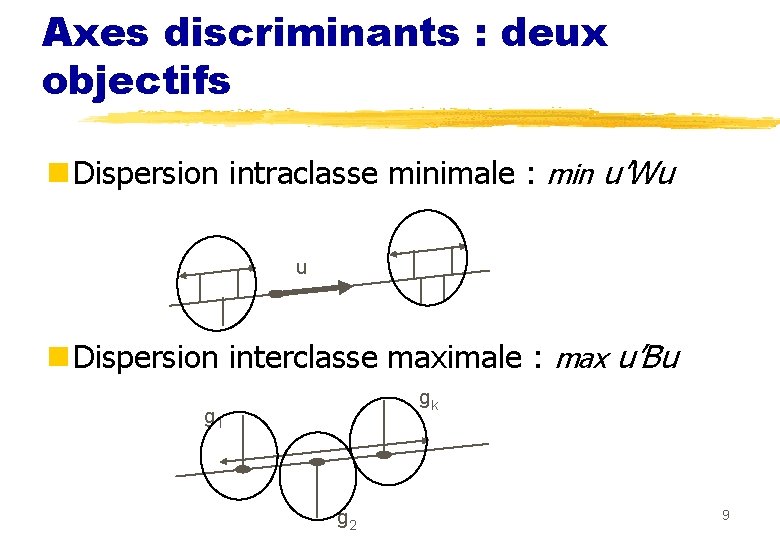
Axes discriminants : deux objectifs n Dispersion intraclasse minimale : min u’Wu u n Dispersion interclasse maximale : max u’Bu gk g 1 g 2 9

n Simultanéité impossible n Compromis : 10

n ACP du nuage des gi avec : n Métrique V-1 n Métrique W-1 Mahalanobis 11

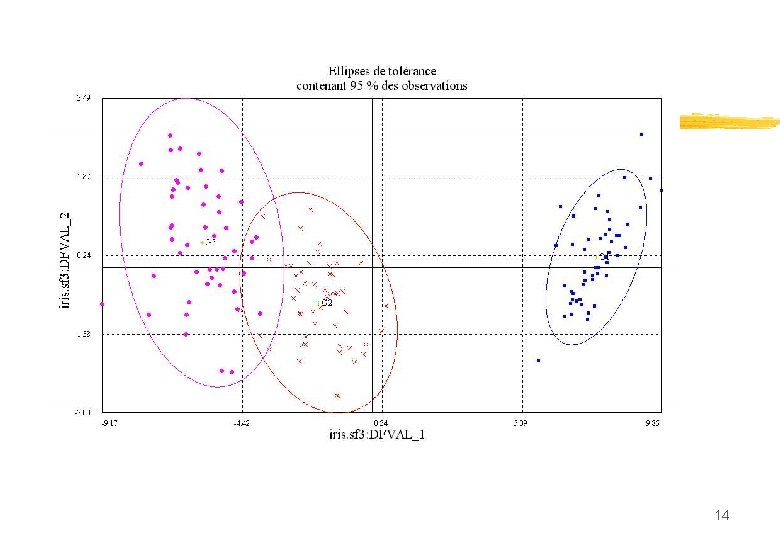
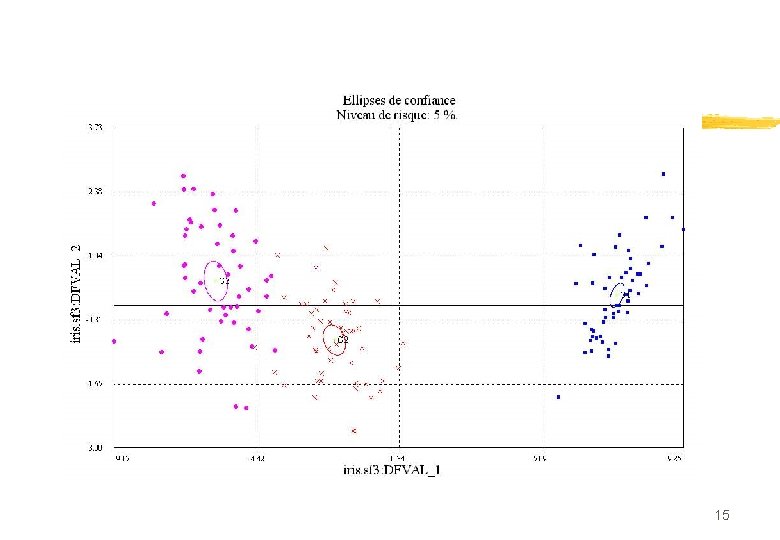
Nombre d’axes discriminants n ACP des groupes : dimension de l’espace contenant les groupes gi n Si n>p>k (cas usuel), k-1 axes discriminants Exemple célèbre : Iris de Fisher • K = 3 Setosa, Versicolor, Virginica • P=4 longueur pétale, longueur sépale, largeur pétale, largeur sépale • n 1=n 2=n 3 =50 Donc deux axes 12

Iris setosa Iris versicolor Iris virginica 13

14

15

Cas de deux groupes n g 1 et g 2 sont sur une droite : 1 seul axe discriminant : e n RAPPEL : en ACP axe a, facteur u = M a a n Combinaison discriminante proportionnelle à M (g 2 - g 1) = W-1 (g 2 - g 1) ou V-1 (g 2 - g 1) n FONCTION DE FISHER : 16

Historique 17

Distance de MAHALANOBIS Dp g 1 g 2 Distance au sens de la métrique W-1. 1. pour p=1 : 2. p quelconque : n Standardisation de chaque composante xj n Décorrélation. . . 18

Équivalence régression 19

Équivalence régression MAIS : Modèle linéaire usuel non valide : en discriminante c’est l’inverse que l’on suppose : 20

Conséquences n. Pas de test, npas d’erreurs standard sur les coefficients n. MAIS possibilité d’utiliser les méthodes de pas à pas en régression. n. Aussi une source de malentendus… 21

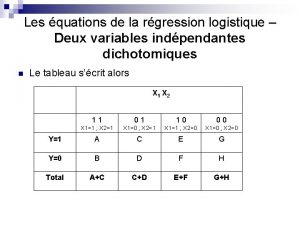
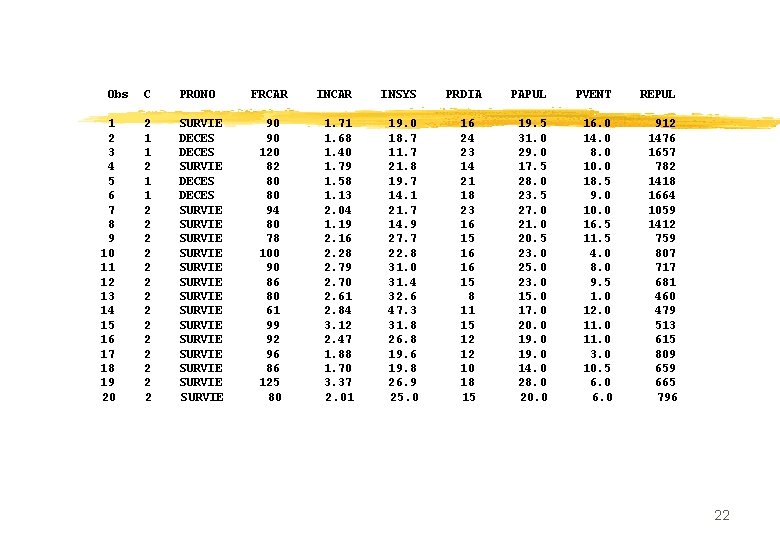
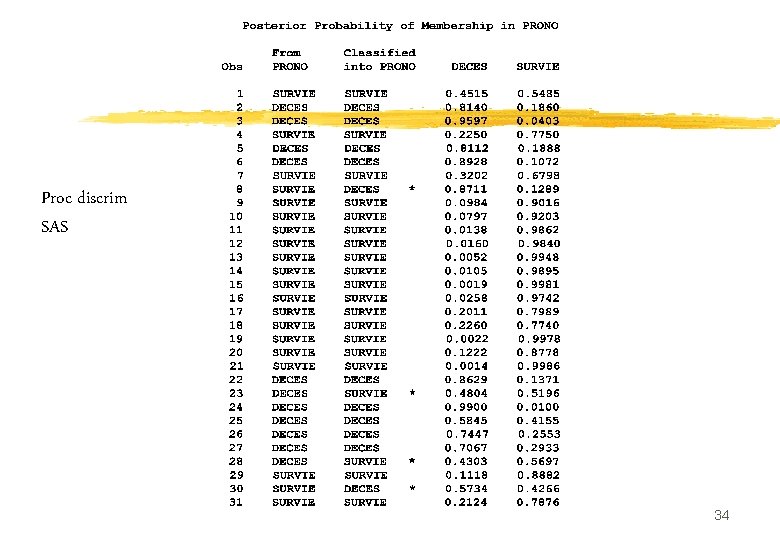
Obs C PRONO FRCAR INSYS PRDIA PAPUL PVENT REPUL 1 2 SURVIE 90 1. 71 19. 0 16 19. 5 16. 0 912 2 1 DECES 90 1. 68 18. 7 24 31. 0 1476 3 1 DECES 120 1. 40 11. 7 23 29. 0 8. 0 1657 4 2 SURVIE 82 1. 79 21. 8 14 17. 5 10. 0 782 5 1 DECES 80 1. 58 19. 7 21 28. 0 18. 5 1418 6 1 DECES 80 1. 13 14. 1 18 23. 5 9. 0 1664 7 2 SURVIE 94 2. 04 21. 7 23 27. 0 1059 8 2 SURVIE 80 1. 19 14. 9 16 21. 0 16. 5 1412 9 2 SURVIE 78 2. 16 27. 7 15 20. 5 11. 5 759 10 2 SURVIE 100 2. 28 22. 8 16 23. 0 4. 0 807 11 2 SURVIE 90 2. 79 31. 0 16 25. 0 8. 0 717 12 2 SURVIE 86 2. 70 31. 4 15 23. 0 9. 5 681 13 2 SURVIE 80 2. 61 32. 6 8 15. 0 1. 0 460 14 2 SURVIE 61 2. 84 47. 3 11 17. 0 12. 0 479 15 2 SURVIE 99 3. 12 31. 8 15 20. 0 11. 0 513 16 2 SURVIE 92 2. 47 26. 8 12 19. 0 11. 0 615 17 2 SURVIE 96 1. 88 19. 6 12 19. 0 3. 0 809 18 2 SURVIE 86 1. 70 19. 8 10 14. 0 10. 5 659 19 2 SURVIE 125 3. 37 26. 9 18 28. 0 665 20 2 SURVIE 80 2. 01 25. 0 15 20. 0 6. 0 796 22

SPAD FONCTION LINEAIRE DISCRIMINANTE VARIABLES CORRELATIONS COEFFICIENTS ECARTS T PROBA. . . . VARIABLES FONCTION REGRESSION TYPES STUDENT NUM LIBELLES AVEC F. L. D. DISC. (RES. TYPE REG. ) (SEUIL= 0. 20). . . . . . 3 FRCAR 0. 232 0. 0588 0. 0133 0. 0092 1. 44 0. 154 4 INCAR -0. 697 -6. 1539 -1. 3887 0. 4966 2. 80 0. 006 5 INSYS -0. 673 0. 1668 0. 0376 0. 0374 1. 01 0. 317 6 PRDIA 0. 474 -0. 0203 -0. 0046 0. 0351 0. 13 0. 897 7 PAPUL 0. 431 0. 1650 0. 0372 0. 0271 1. 37 0. 173 8 PVENT 0. 269 0. 0469 0. 0106 0. 0176 0. 60 0. 549 9 REPUL 0. 650 -0. 0002 0. 0000 0. 0002 0. 19 0. 849 CONSTANTE -1. 604374 -0. 367565 0. 9373 0. 3922 0. 6958. . . . . . R 2 = 0. 55759 F = 16. 74489 PROBA = 0. 000 D 2 = 4. 94213 T 2 = 124. 77643 PROBA = 0. 000. . . . . . 23

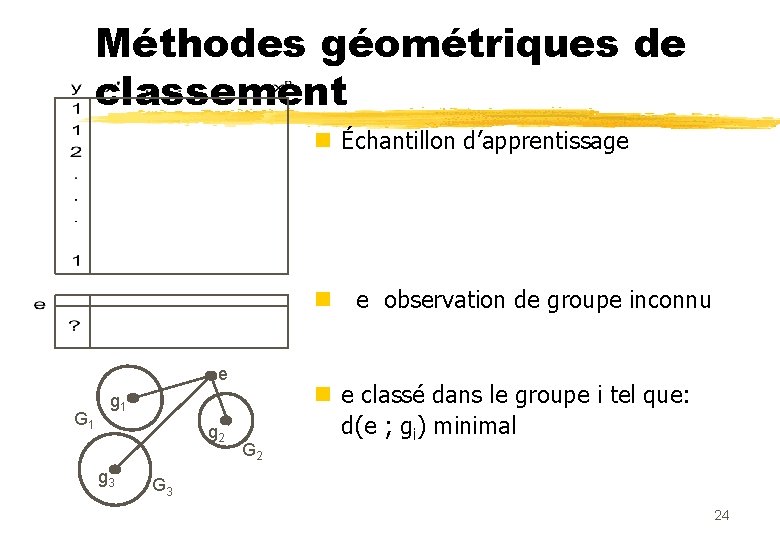
Méthodes géométriques de classement n Échantillon d’apprentissage n e observation de groupe inconnu e G 1 g 2 g 3 G 2 n e classé dans le groupe i tel que: d(e ; gi) minimal G 3 24

pour deux groupes n On classe dans G 1 si: n Fonction de Fisher >c n Score de Fisher: 25

Interprétation géométrique n Projection sur la droite des centres avec la métrique W-1 n Dualité axe-frontière plane frontière axe discriminant 26

Analyse discriminante probabilis 27

La règle bayésienne naïve dans le cadre normal 28

La règle bayésienne 29

Analyse discriminante probabiliste: cas de deux groupes 30

Fonction de score et probabilité n Fonction de score S(x) : Règle : affecter au groupe 1 si S(x)>0 n Probabilité d’appartenance au groupe 1 : 31

Probabilité a posteriori 32

S(x) • Probabilité d’erreur de classement de G 2 en G 1 : On classe en G 1 si S(x)>0 33

Proc discrim SAS 34

II: La régression logistique II. 1 Le modèle logistique simple II. 2 Odds ratios II. 3 Interprétation économètrique II. 4 Estimation II. 5 Tests 35

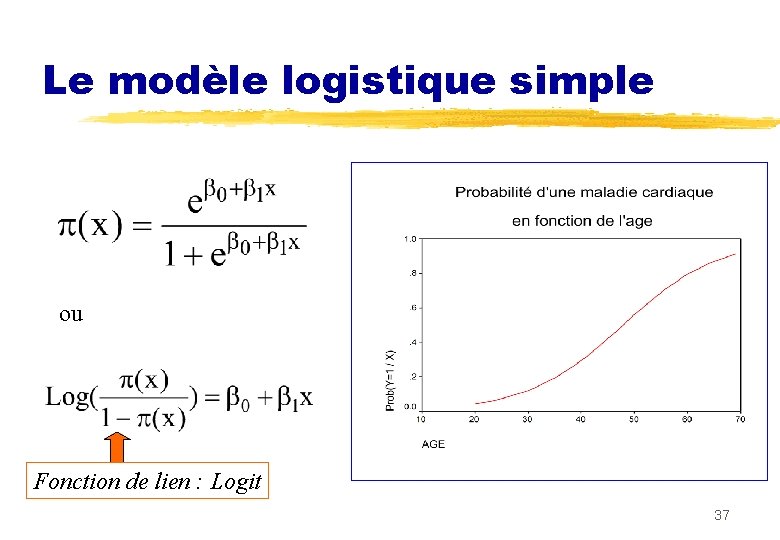
II. 1 Le modèle logistique simple n Réponse dichotomique : Y = 0 / 1 n Variable explicative : X n Objectif : Modéliser (x) = Prob(Y = 1/X = x) • Le modèle linéaire (x) = 0 + 1 x convient mal lorsque X est continue. • Le modèle logistique est plus naturel 36

Le modèle logistique simple ou Fonction de lien : Logit 37

n Il s’agit bien d’un probléme de régression: n Modélisation de l’espérance conditionnelle n E(Y/X=x)=f(x) n Choix de la forme logistique en épidémiologie: n S’ajuste bien n Interprétation de 1 en termes d’odds-ratio 38

II. 2 Odds-Ratio Si X binaire (sujet exposé X=1, non exposé X=0) 39

Odds-Ratio n Mesure l’évolution du rapport des chances d’apparition de l’événement Y=1 contre Y=0 (la cote des parieurs) lorsque X passe de x à x+1. n Formule générale: 40

II. 3 Interprétation économètrique n Y possession d’un bien durable par un ménage: manifestation visible d’une variable latente Z inobservable continue. n Z est l’ « intensité du désir » de posséder le bien n Si Z<seuil Y=0, sinon Y=1 n Le seuil peut être choisi égal à 0 41

Modèle d’utilité n pour le ménage i de caractéristiques xi (âge, sexe, revenu, CSP. . . ), la possession du bien procure un niveau d’utilité U(1, xi), la non possession U(0, xi). Yi = 1 U(1, xi) > U(0, xi) Yi = 0 U(0, xi) > U(1, xi) n Variable latente Zi = U(1, xi) – U(0, xi). 42

Modèle d’utilité (suite) n Zi = xi + i n πi = P(Yi=1|xi)= P(Zi > 0)=P(xi > - i) = F(xi ) n F fonction de répartition de - i n Choix de F: n Logistique : modèle logit, régression logistique n Normal: modèle probit 43

II. 4 Estimation des paramètres Les données Le modèle yi = 1 si caractère présent, 0 sinon 44

Vraisemblance (conditionnelle!) Probabilité d’observer les données [(x 1, y 1), …, (xi, yi), …, (xn, yn)] 45

maximum de vraisemblance n maximisent n Maximisation de la log-vraisemblance n Estimateurs obtenus par des procédures numériques: pas d’expression analytique 46

Précision (asymptotique) des estimateurs n La matrice estimée par la matrice 47
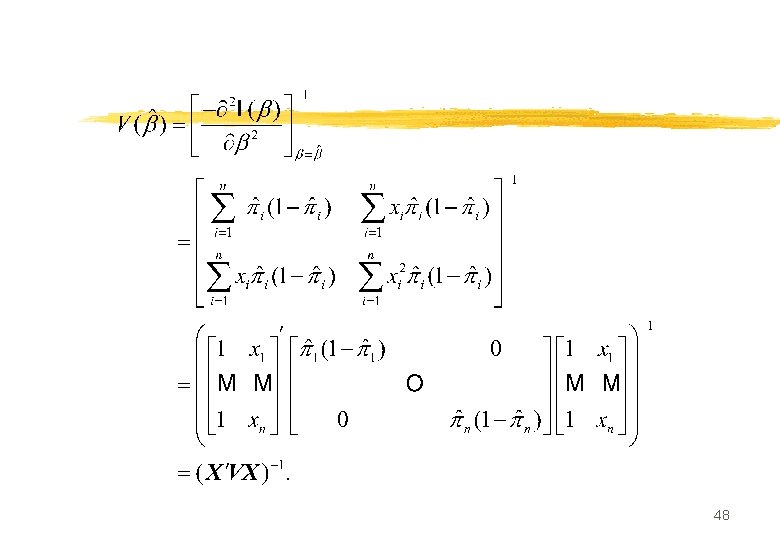
48

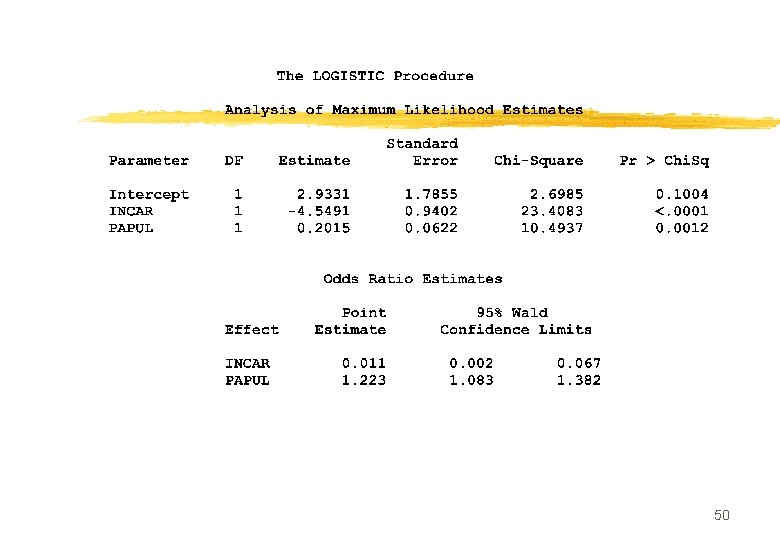
Régression logistique multiple n Généralisation à p variables explicatives X 1, …, Xp. 49

50

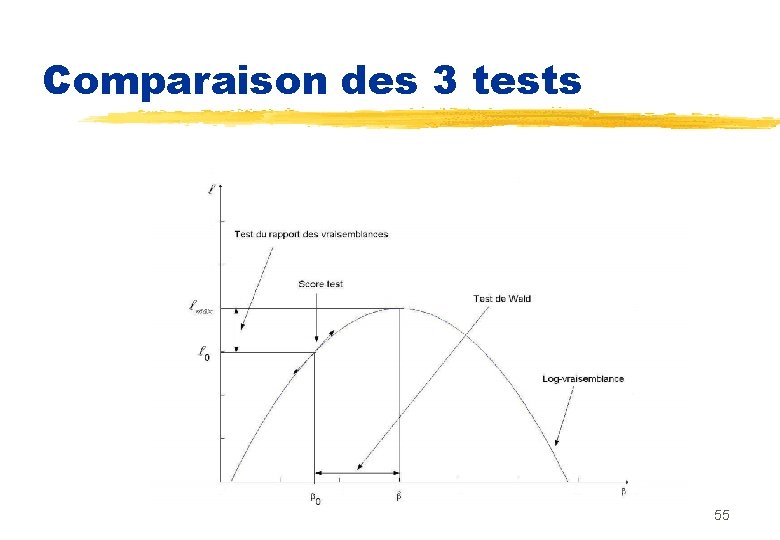
II. 5 Tests sur les paramètres n Trois méthodes sont disponibles pour tester l’apport de la variable X au modèle : 1. Le test de Wald 2. La méthode du rapport de vraisemblance 3. Le test du score 51

Test de Wald n analogue à un test de Student en régression usuelle, si l’on considère la statistique w définie par : n représente l’estimation de l’écart-type de l’estimateur de 1. n Sous l’hypothèse H 0, w 2 suit approximativement une loi du khi-deux à un degré de liberté. n Rejet de H 0 si w 2 52

Test du rapport des vraisemblances n L’apport de la variable X est mesuré à l’aide de la statistique : G = -2 log [ ] sous l’hypothèse H 0 G suit asymptotiquement une loi du khi-deux à un degré de liberté. n Vraisemblance sans la variable: 53

Test du score n U vecteur des dérivées partielles de la logvraisemblance estimées n Le score suit également asymptotiquement sous H 0 une loi du khi-deux à un degré de liberté n En régression logistique simple, le score est égal à nr 2 , où r est le coefficient de corrélation linéaire (abusif!) entre Y et X 54

Comparaison des 3 tests 55

Tests n Tests d’absence d’effet de toutes les variables: H 0 : 1 = …… = p = 0 n Rapport de vraisemblance G n Score test U n Sous H 0, suivent tous deux asymptotiquement une loi du 2 à p ddl 56

III Discrimination sur variables qualitatives et scoring 57

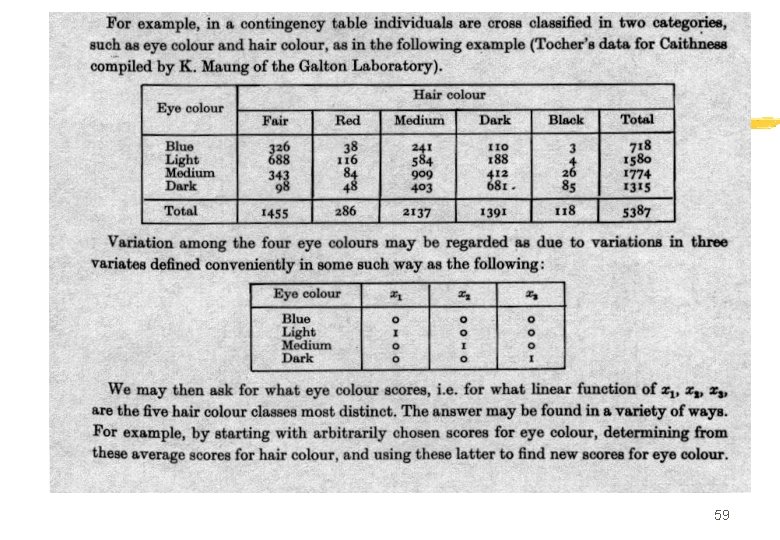
Un peu de (pré)histoire n Fisher (1940) n Un seul prédicteur n Equations de l’AFC n « Scores » were introduced 58

59

60

Cas général p prédicteurs n Quantification optimale: n Donner des scores partiels aux catégories pour maximiser la distance de Mahalanobis dans Rp n Une analyse discriminante où les variables qualitatives sont remplacées par des indicatrices =X 61

n X n’est pas de plein rang: rank(X)= mi-p n Solution classique: éliminer une indicatrice par prédicteur n Disqual (Saporta, 1975): • ADL effectuée sur une sélection de facteurs de l’ACM de X. Analogue de la régression sur composantes principales 62

DISQUAL 1ère étape n Analyse des correspondances du tableau des prédicteurs. n k variables numériques : garder les coordonnées factorielles plus discriminantes 63

2ème étape : n Analyse discriminante linéaire (Fisher). n Score = combinaison linéaire des coordonnées factorielles= combinaison linéaire des indicatrices des catégories n Coefficients = grille de notation n 64

Sélection des axes n Selon l’ordre de l’ACM n % d’inertie n Selon le pouvoir discriminant n Student sur 2 groupes, F sur k groupes 65

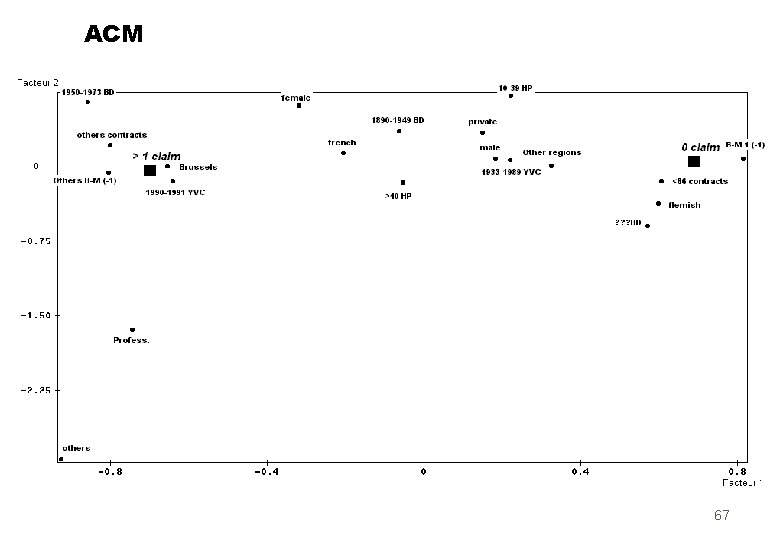
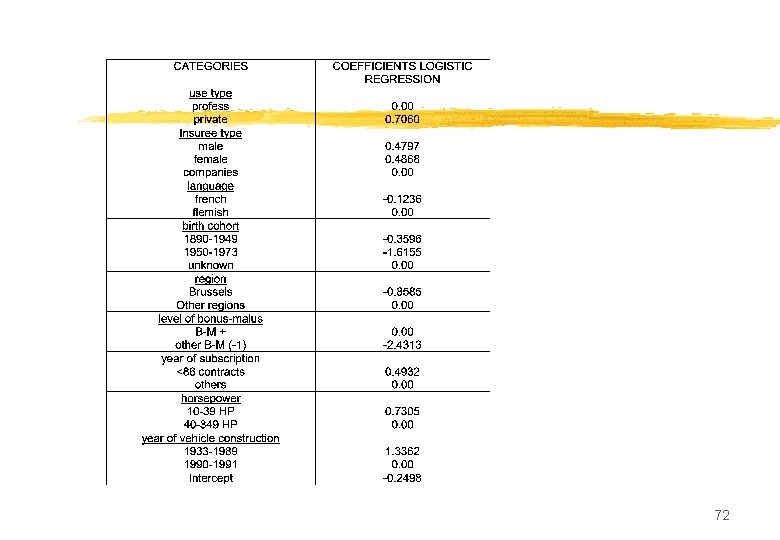
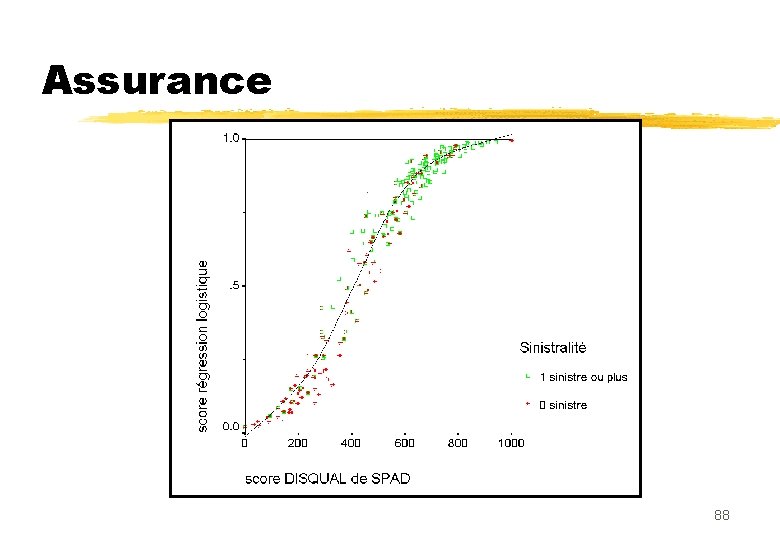
Example assurance (SPAD) n 1106 contrats automobile belges: n 2 groupes: « 1 bons» , « 2 mauvais » n 9 prédicteurs: 20 catégories n Usage (2), sexe (3), langue (2), age (3), région (2), bonus-malus (2), puissance (2), durée (2), age du véhicule (2) 66

ACM 67

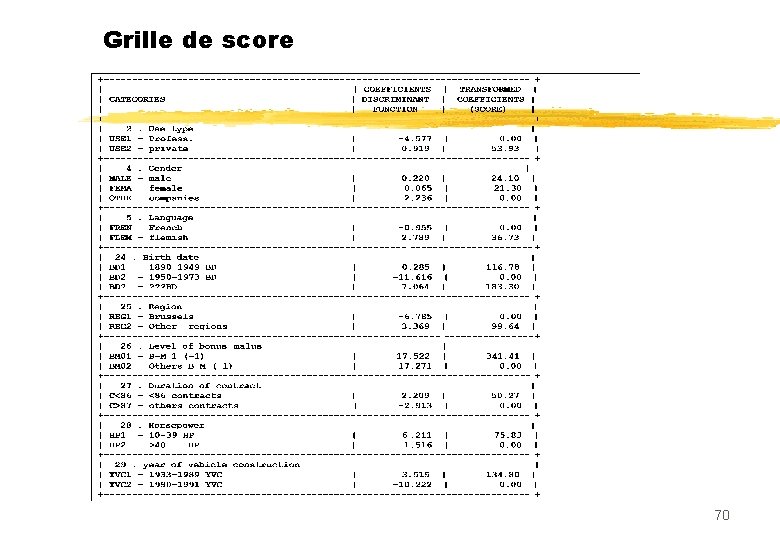
ADL de Fisher sur les composantes FACTEURS CORRELATIONS COEFFICIENTS . . . . . 1 F 1 0. 719 6. 9064 2 F 2 0. 055 0. 7149 3 F 3 -0. 078 -0. 8211 4 F 4 -0. 030 -0. 4615 5 F 5 0. 083 1. 2581 6 F 6 0. 064 1. 0274 7 F 7 -0. 001 0. 2169 8 F 8 0. 090 1. 3133 9 F 9 -0. 074 -1. 1383 10 F 10 -0. 150 -3. 3193 11 F 11 -0. 056 -1. 4830 CONSTANTE 0. 093575 . . . . . R 2 = 0. 57923 F = 91. 35686 D 2 = 5. 49176 T 2 = 1018. 69159 . . . . . Score= 6. 90 F 1 - 0. 82 F 3 + 1. 25 F 5 + 1. 31 F 8 - 1. 13 F 9 - 3. 31 F 10 68

n scores normalisés n Echelle de 0 à 1000 n Transformation linéaire du score et du seuil 69

Grille de score 70

Scoring et régression logistique n Inclusion aisée de prédicteurs qualitatifs en introduisant mi-1 indicatrices n Modalité omise= modalité de référence. Attention à l’interprétation n Standard de l’industrie bancaire (sauf Banque de France) 71

72

IV Comparaison logistiquediscriminante n Avantages proclamés de la logistique: n Interprétabilité des coefficients (odds-ratios) n Erreurs standard calculables n Modélisation des probabilités n Hypothèses plus générales qu’en AD gaussienne n Maximum de vraisemblance au lieu de moindres carrés (régression linéaire de Y sur les Xj) n Prise en charge facile des X qualitatifs (logiciels) 73

n Mais: n Erreurs standard asymptotiques , bootstrap en AD n Non convergence en cas de séparation parfaite. Fisher existe toujours n Maximum de vraisemblance conditionnel: non optimal dans le cas gaussien standard n L’AD peut aussi traiter les variables qualitatives, et de manière plus robuste grâce aux contraintes de sous-espace (Disqual) 74

n Querelle largement idéologique (modélisation versus analyse des données) n L’AD est aussi un modèle, mais sur les lois des X/Y, la logistique sur les lois de Y/X n En pratique différences peu nettes: fonctions de score souvent très proches n « It is generally felt that logistic regression is a safer, more robust bet than the LDA model, relying on fewer assumptions. It is our experience that the models give very similar results , even when LDA is used in inappropriately, such as with qualitative variables. » Hastie and al. (2001) 75

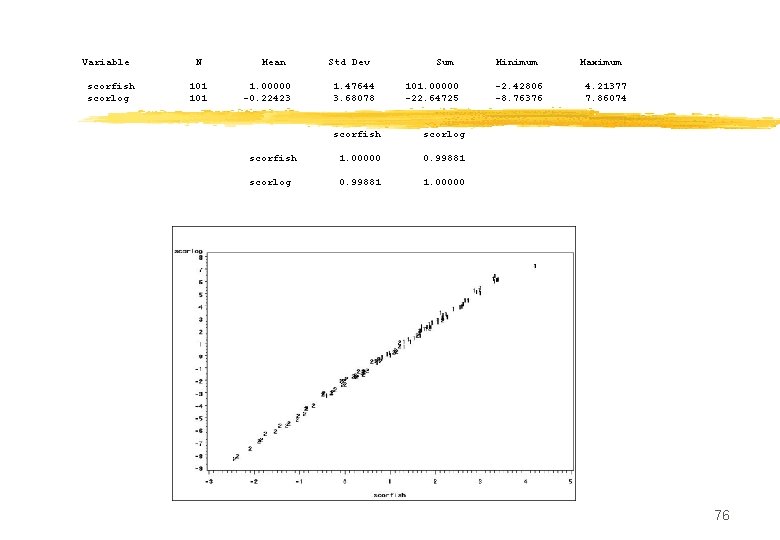
Variable N Mean Std Dev Sum Minimum Maximum scorfish 101 1. 00000 1. 47644 101. 00000 -2. 42806 4. 21377 scorlog 101 -0. 22423 3. 68078 -22. 64725 -8. 76376 7. 86074 scorfish scorlog scorfish 1. 00000 0. 99881 scorlog 0. 99881 1. 00000 76

n Usages souvent différents: AD pour classer, logistique pour modéliser (facteurs de risque) n Logistique aussi utilisée en scoring n Si l’objectif est de classer: n On ne fait plus de la science mais de l’aide à la décision n Mieux vaut essayer les deux méthodes. n Mais comment les comparer? n Le vrai critère de choix est la performance en généralisation 77

Qualité d’une règle de classement n Tableau de classement : n On classe des observations dont le groupe est connu : n Pourcentage de bien classés : n Taux d’erreur de classement : 78

Sur quel échantillon faire ce tableau ? n Échantillon test d’individus supplémentaires. n Si on reclasse l’échantillon ayant servi à construire la règle (estimation des coefficients) : «méthode de resubstitution» BIAIS n surestimation du pourcentage de bien classés. n Solutions pour des échantillons de petite taille : Validation croisée ou bootstrap 79

Seuil et probabilités a posteriori n P(G 1/x) dépend des probas a priori p 1 et p 2 n Problèmes de l’échantillonnage stratifié n poser priors = en discrim ou pevent= en Logistic n sinon probas a posteriori fausses n seul le terme constant 0 est modifié: on ajoute ln(p 2/p 1) n Sans importance pour un score 80

Qualité d’un score n Qu’il soit obtenu par Fisher ou logistique: n Comparaison des distributions du score sur les deux groupes n fonctions de répartition 81

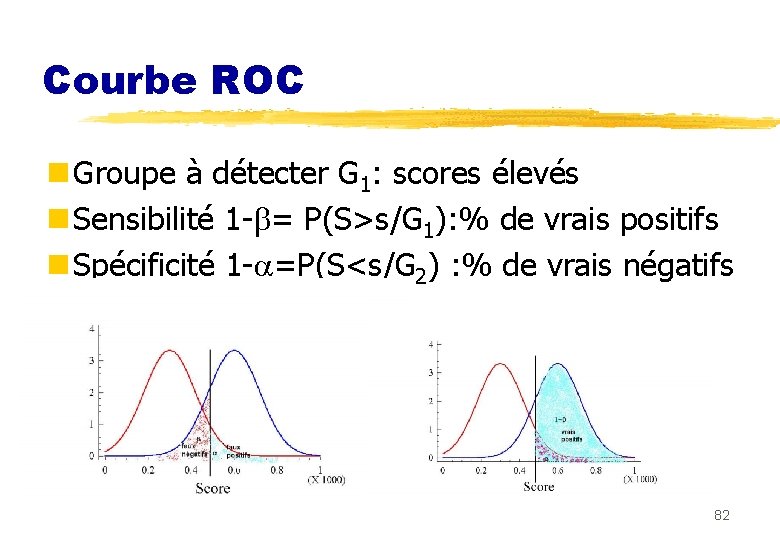
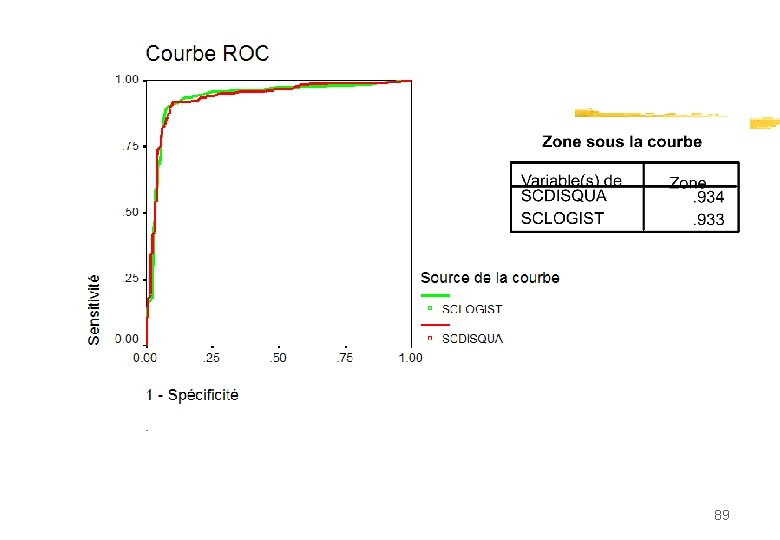
Courbe ROC n Groupe à détecter G 1: scores élevés n Sensibilité 1 - = P(S>s/G 1): % de vrais positifs n Spécificité 1 - =P(S<s/G 2) : % de vrais négatifs 82

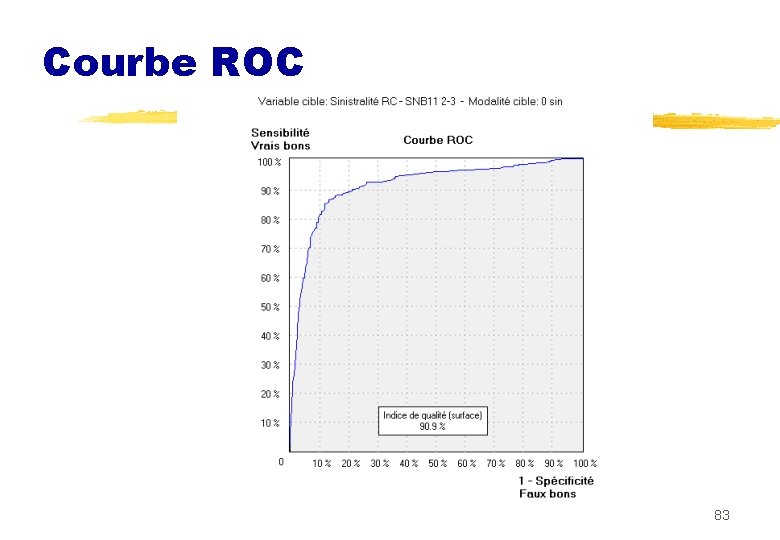
Courbe ROC 83

Courbe ROC n Evolution de 1 - puissance du test en fonction de , risque de première espèce lorsque le seuil varie n Proportion de vrais positifs en fonction de la proportion de faux positifs n Un site: http: //www. anaesthetist. com/mnm/stats/roc/ 84

n Courbe ROC invariante pour toute transformation monotone croissante n Surface sous la courbe: mesure de performance permettant de comparer (partiellement) des modèles n On tire une obs de G 1 et une de G 2 n AUC estimée par la proportion de paires concordantes n nc statistique de Wilcoxon-Mann-Whitney U+W= n 1 n 2+0. 5 n 1(n 1+1) AUC=U/n 1 n 2 85

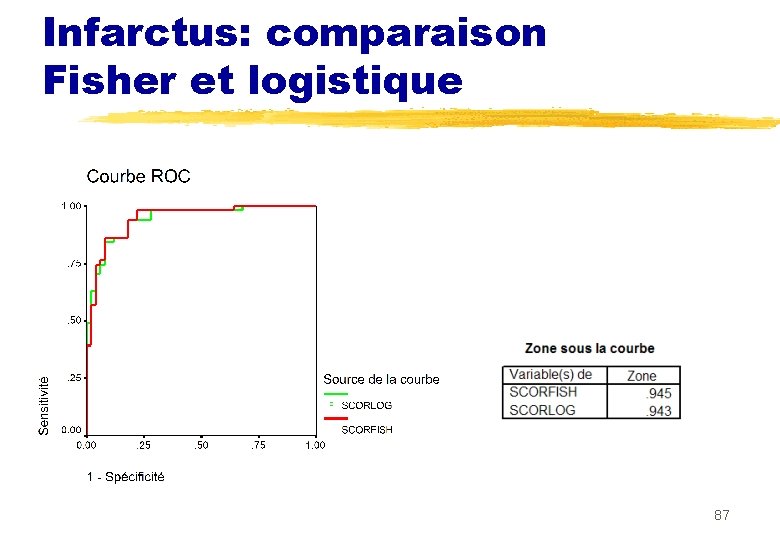
Exemple infarctus proc logistic Association des probabilités prédites et des réponses observées Pairs 2550 Percent Concordant 94. 3 Percent Discordant 5. 7 Percent Tied 0. 0 Somers' D 0. 886 Gamma 0. 886 Tau-a 0. 447 c 0. 943 86

Infarctus: comparaison Fisher et logistique 87

Assurance 88

89

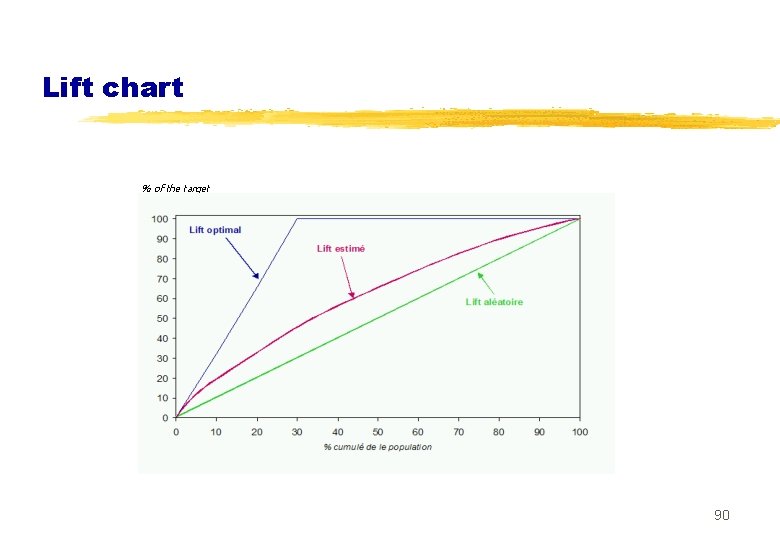
Lift chart % of the target 90

Surface sous la courbe de lift n Proportion des unités ayant un score>s n Surface: 91

Coefficient Ki (Kxen) n Ki=(aire entre courbe lift et diagonale) / (aire entre courbe lift et courbe idéale) Ki=Somers’ D ou Accuracy Ratio AR 92

n Optimiser AUC ou Ki: mêmes résultats. n Ne prend pas en compte les coûts n Ne pas comparer sur données d’apprentissage… 93

Les 3 échantillons n Apprentissage: pour estimer les paramètres des modèles n Test : pour choisir le meilleur modèle n Validation : pour estimer la performance sur des données futures n Nécessité de faire plusieurs tirages n Modèle final: avec toutes les observations 94

Conclusion n ADL et régression logistique: fondements également solides mais différents n Un faux débat s’il s’agit seulement de prédire. n Convergence des pratiques : n validation en logistique n Courbe ROC en discriminante n Prudence quand on calcule des probabilités: n Vraies probas ou simples scores 95
 Comparatif de bien
Comparatif de bien Comparaisons
Comparaisons Clasificax
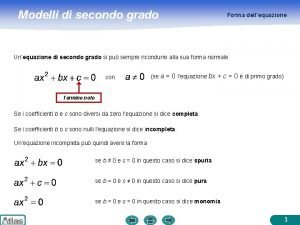
Clasificax Quadratic function
Quadratic function Fórmula resolvente simplificada
Fórmula resolvente simplificada Dominio di un'equazione di secondo grado
Dominio di un'equazione di secondo grado Funcion discriminante de maddrey
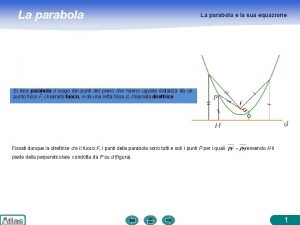
Funcion discriminante de maddrey Parabola discriminante
Parabola discriminante La longitud del hilo que sostiene una cometa es de 250
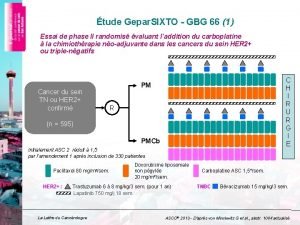
La longitud del hilo que sostiene una cometa es de 250 Logistique traitement pmcb
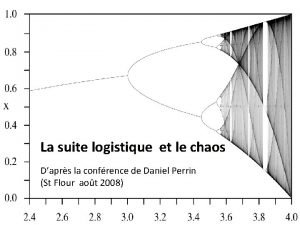
Logistique traitement pmcb Suite logistique
Suite logistique Bescos logistique
Bescos logistique Optimisation plateforme logistique
Optimisation plateforme logistique Magento gestion stock
Magento gestion stock Logistique mode
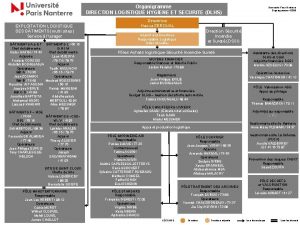
Logistique mode Organigramme direction logistique
Organigramme direction logistique Logistique promotionnelle pontarlier
Logistique promotionnelle pontarlier Gerbage en palettier
Gerbage en palettier Logistique interne chaine de valeur
Logistique interne chaine de valeur Observatoire marocain de la compétitivité logistique
Observatoire marocain de la compétitivité logistique Cahier des charges logistique
Cahier des charges logistique Supply chain management définition
Supply chain management définition Projet bts gtla exemple
Projet bts gtla exemple Abc analyse berekenen
Abc analyse berekenen Diagramme pieuvre scooter
Diagramme pieuvre scooter Homo faber analyse textstelle
Homo faber analyse textstelle Exemple d'analyse environnementale iso 14001 version 2015
Exemple d'analyse environnementale iso 14001 version 2015 Analyse af kortfilm
Analyse af kortfilm Phonologische analyse
Phonologische analyse Datamatrice
Datamatrice Begeleidingsstijlen in de zorg
Begeleidingsstijlen in de zorg Atg
Atg Gevinst
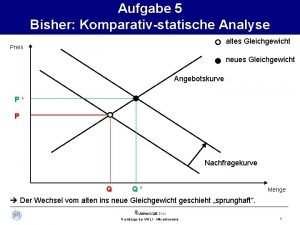
Gevinst Komparativ statische analyse
Komparativ statische analyse Analyse the extent
Analyse the extent Lead user analyse
Lead user analyse La dépouille du minotaure en costume d'arlequin analyse
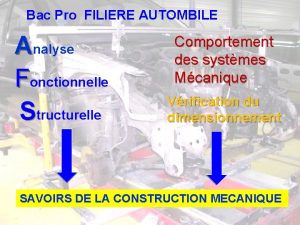
La dépouille du minotaure en costume d'arlequin analyse Analyse fonctionnelle et structurelle bac pro
Analyse fonctionnelle et structurelle bac pro Dejlig er den himmel blå analyse
Dejlig er den himmel blå analyse Analyse fonctionnelle robot tondeuse
Analyse fonctionnelle robot tondeuse Otto scharff
Otto scharff Gleich nach dem losfahren machen sie eine bremsprobe warum
Gleich nach dem losfahren machen sie eine bremsprobe warum Analyse fonctionnelle bete à corne
Analyse fonctionnelle bete à corne Financiële analyse
Financiële analyse Pestel-analyse beispiel automobilindustrie
Pestel-analyse beispiel automobilindustrie Profibus analyse
Profibus analyse Le mauvais vitrier
Le mauvais vitrier Medea analyse
Medea analyse Aufbau kurzgeschichten interpretation
Aufbau kurzgeschichten interpretation Oradour sur glane poeme
Oradour sur glane poeme Kraljic matrisen
Kraljic matrisen Lyrik prosa
Lyrik prosa Analyse af kvantitative data
Analyse af kvantitative data Aktantmodellen askepot
Aktantmodellen askepot Uautentisk
Uautentisk Nachtgedanken heinrich heine interpretation
Nachtgedanken heinrich heine interpretation Slogan of chanel
Slogan of chanel Ekstern analyse
Ekstern analyse Ekstern analyse strategi
Ekstern analyse strategi Ciel, air et vents, plains et monts découverts analyse
Ciel, air et vents, plains et monts découverts analyse Diagramme pieuvre segway
Diagramme pieuvre segway Männer herbert grönemeyer analyse
Männer herbert grönemeyer analyse Brief aus amerika analyse
Brief aus amerika analyse Analyse partitionnelle
Analyse partitionnelle Analyse des dangers
Analyse des dangers Social return on investment beispiel
Social return on investment beispiel Il est dix heures o ma pauvre petite fille
Il est dix heures o ma pauvre petite fille Blocus de berlin
Blocus de berlin Otto dix assaut sous les gaz analyse
Otto dix assaut sous les gaz analyse Residu analyse
Residu analyse Marc groet s morgens de dingen analyse
Marc groet s morgens de dingen analyse Trümmer und kahlschlagliteratur
Trümmer und kahlschlagliteratur Analyse numérique
Analyse numérique Analyse af det røde gardin
Analyse af det røde gardin La vierge du chancelier rolin analyse
La vierge du chancelier rolin analyse Higher pe cycle of analysis
Higher pe cycle of analysis Analyse portefeuille d'activité
Analyse portefeuille d'activité Pilgrimskor
Pilgrimskor Cepstre
Cepstre La famille des cochons ramenée dans l'étable analyse
La famille des cochons ramenée dans l'étable analyse Weende analyse
Weende analyse Analyse en constituants immédiats
Analyse en constituants immédiats Analyse swot tupperware
Analyse swot tupperware Der fremde freund drachenblut film
Der fremde freund drachenblut film Analyse zi fdf
Analyse zi fdf Centraltendens
Centraltendens Guernica picasso analyse
Guernica picasso analyse Agnes peter stamm analyse
Agnes peter stamm analyse Function point verfahren
Function point verfahren Multivariat analyse
Multivariat analyse Wat is een situatieanalyse
Wat is een situatieanalyse Destep analyse template
Destep analyse template Amortisierte analyse
Amortisierte analyse Concept de virginia henderson
Concept de virginia henderson Goethe gefunden
Goethe gefunden Cos swot
Cos swot