6 ANLISIS DISCRIMINANTE Introduccin Regla discriminante lineal de

6. ANÁLISIS DISCRIMINANTE § Introducción § Regla discriminante lineal de Fisher Versión poblacional § Versión muestral § § El problema general de clasificación para dos poblaciones Probabilidad a priori § Costes de clasificación § Coste esperado por mala clasificación § Regiones óptimas § 1

6. ANÁLISIS DISCRIMINANTE § Clasificación para dos poblaciones normales § Versión poblacional § Versión muestral § Clasificación general para g poblaciones Costes de clasificación § Coste esperado por mala clasificación § Regiones óptimas § 2

6. ANÁLISIS DISCRIMINANTE § Clasificación para g poblaciones normales Score cuadrático de clasificación § Versión muestral § § Clasificación para g poblaciones normales con matrices de covarianzas iguales Score lineal de clasificación § Versión muestral § 3

Introducción Supervisada: Análisis discriminante Clasificación No supervisada: Análisis de conglomerados (clustering) El análisis discriminante es una técnica de clasificación para asignar nuevas observaciones a grupos ya conocidos. ANÁLISIS DISCRIMINANTE 4

Regla discriminante lineal de Fisher Sea la variable Sean y dos poblaciones y y Se busca una combinación lineal de la forma que sea óptima para clasificar una observación en alguna de las dos poblaciones. ANÁLISIS DISCRIMINANTE 5

Regla discriminante lineal de Fisher Se tiene que ANÁLISIS DISCRIMINANTE 6

Regla discriminante lineal de Fisher Hay que buscar l que optimice la separación entre las dos poblaciones: se maximiza la separación entre las medias: ANÁLISIS DISCRIMINANTE 7

Regla discriminante lineal de Fisher Si se maximiza sin restricciones, el máximo puede no ser finito: se maximiza dividiendo por la varianza Nota: es común. La solución que se obtiene es: Función discriminante lineal de Fisher ANÁLISIS DISCRIMINANTE 8

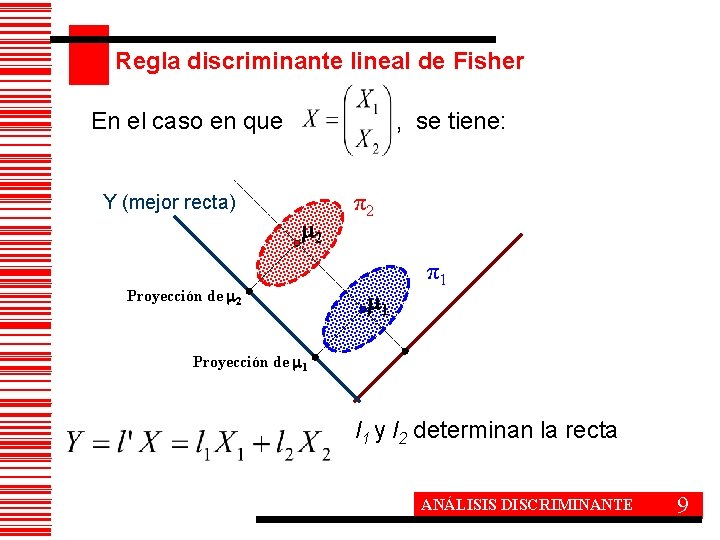
Regla discriminante lineal de Fisher En el caso en que Y (mejor recta) , se tiene: 2 Proyección de 2 π2 1 π1 Proyección de 1 l 1 y l 2 determinan la recta ANÁLISIS DISCRIMINANTE 9

Regla discriminante lineal de Fisher El punto medio es: 2 Y=l’X Y 2 m l’x 0 Y 1 Dada una nueva observación x 0: 1 § Asignar x 0 a π1 si § Asignar x 0 a π2 si ANÁLISIS DISCRIMINANTE 10

Regla discriminante lineal de Fisher Proposición ANÁLISIS DISCRIMINANTE 11

Regla discriminante lineal de Fisher: Versión muestral Dadas dos poblaciones y , se tienen las siguientes matrices de datos: y sean Nota: no es necesario n 1=n 2 ANÁLISIS DISCRIMINANTE 12

Regla discriminante lineal de Fisher: Versión muestral La regla lineal es: Función discriminante lineal muestral de Fisher que es óptima para clasificar entre las dos poblaciones. El punto medio es: ANÁLISIS DISCRIMINANTE 13

Regla discriminante lineal de Fisher: Versión muestral Y=l’X Y 2 m l’x 0 Y 1 Dada una nueva observación x 0 , la regla de clasificación sería: § Asignar x 0 a π1 si § Asignar x 0 a π2 si ANÁLISIS DISCRIMINANTE 14

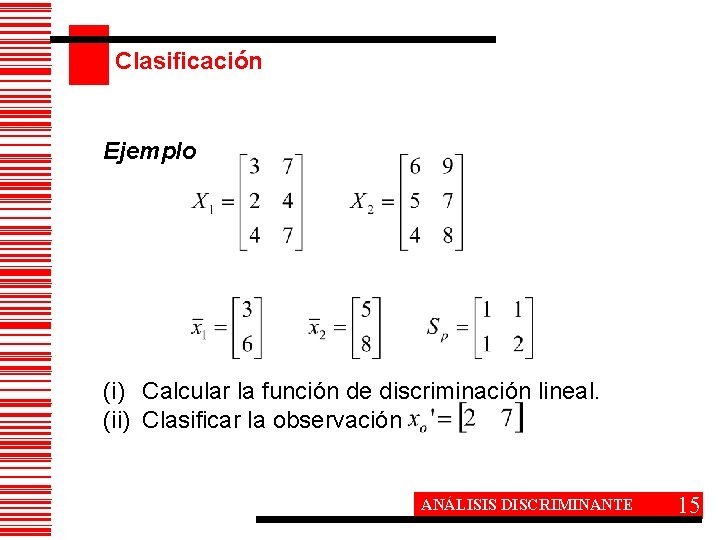
Clasificación Ejemplo (i) Calcular la función de discriminación lineal. (ii) Clasificar la observación ANÁLISIS DISCRIMINANTE 15

El problema general de clasificación para dos poblaciones Dada la variable y dos poblaciones siendo f 1 la función de densidad de y y f 2 la función de densidad de ANÁLISIS DISCRIMINANTE 16

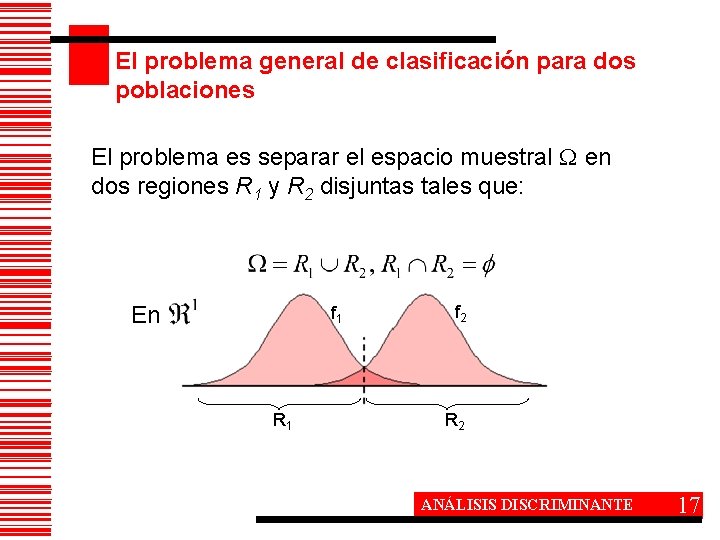
El problema general de clasificación para dos poblaciones El problema es separar el espacio muestral en dos regiones R 1 y R 2 disjuntas tales que: En f 1 R 1 f 2 R 2 ANÁLISIS DISCRIMINANTE 17

El problema general de clasificación para dos poblaciones § Probabilidad de clasificar en si viene de ANÁLISIS DISCRIMINANTE 18

El problema general de clasificación para dos poblaciones § p 1 : probabilidad de que venga de § p 2 : probabilidad de que venga de § P(clasificar correctamente en )= § P(clasificar incorrectamente en § P(clasificar correctamente en )= )= § P(clasificar incorrectamente en )= ANÁLISIS DISCRIMINANTE 19

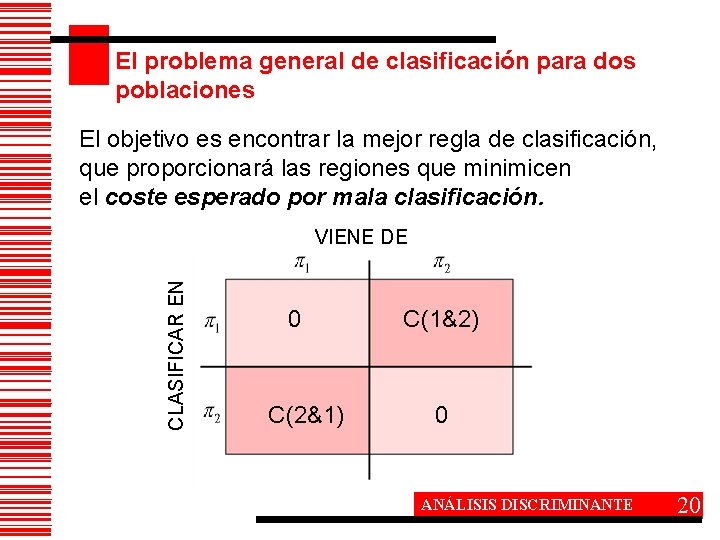
El problema general de clasificación para dos poblaciones El objetivo es encontrar la mejor regla de clasificación, que proporcionará las regiones que minimicen el coste esperado por mala clasificación. CLASIFICAR EN VIENE DE 0 C(2&1) C(1&2) 0 ANÁLISIS DISCRIMINANTE 20

El problema general de clasificación para dos poblaciones El coste esperado por mala clasificación para dos regiones es: El objetivo es hallar dos regiones que minimicen el CEMC. ANÁLISIS DISCRIMINANTE 21

El problema general de clasificación para dos poblaciones Teorema Las regiones R 1 y R 2 que minimizan el coste esperado por mala clasificación son: ANÁLISIS DISCRIMINANTE 22

El problema general de clasificación para dos poblaciones Corolario § p 1 = p 2 § C(1&2) = C(2&1) ANÁLISIS DISCRIMINANTE 23

El problema general de clasificación para dos poblaciones § p 1= p 2 y C(1&2) = C(2&1) ANÁLISIS DISCRIMINANTE 24

Clasificación para dos poblaciones normales En este caso se conoce la función de densidad para Dada la variable con y las dos poblaciones , respectivamente, el objetivo es hallar las dos regiones R 1 y R 2 que minimizan el CEMC. ANÁLISIS DISCRIMINANTE 25

Clasificación para dos poblaciones normales Teorema Las regiones R 1 y R 2 que minimizan el CEMC son: siendo ANÁLISIS DISCRIMINANTE 26

Clasificación para dos poblaciones normales Observación § Si la regla de clasificación es cuadrática. se obtienen las regiones: ANÁLISIS DISCRIMINANTE 27

Clasificación para dos poblaciones normales Si se considera , entonces se llega a la regla discriminante lineal de Fisher. ANÁLISIS DISCRIMINANTE 28

Clasificación para dos poblaciones normales Versión muestral Dadas dos poblaciones y las matrices de datos Nota: no es necesario n 1= n 2 ANÁLISIS DISCRIMINANTE 29

Clasificación para dos poblaciones normales: Versión muestral estimando y , se tiene: ANÁLISIS DISCRIMINANTE 30

Clasificación general para g poblaciones Sea la variable siendo y y las g poblaciones sus respectivas funciones de densidad las probabilidades a priori. ANÁLISIS DISCRIMINANTE 31

Clasificación general para g poblaciones El coste de clasificar en C(i&k), siendo C(i&i) = 0, viniendo de es Las g regiones en las se puede clasificar vienen dadas por: ANÁLISIS DISCRIMINANTE 32

Clasificación general para g poblaciones La probabilidad de clasificar en si viene de es ANÁLISIS DISCRIMINANTE 33

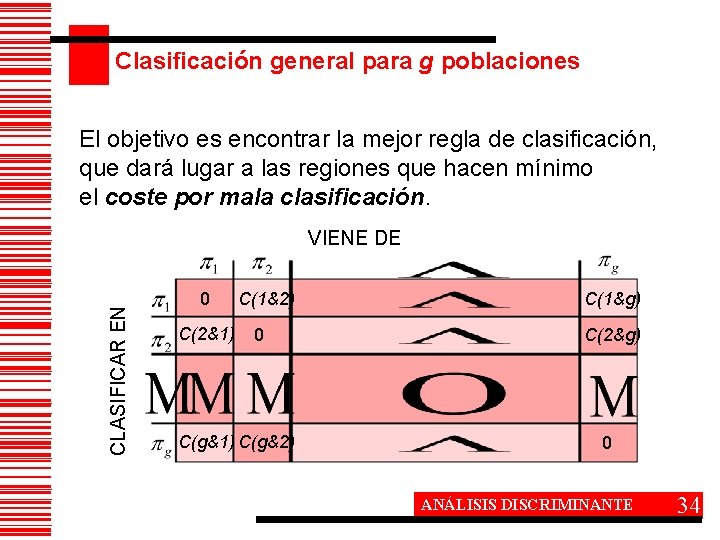
Clasificación general para g poblaciones El objetivo es encontrar la mejor regla de clasificación, que dará lugar a las regiones que hacen mínimo el coste por mala clasificación. CLASIFICAR EN VIENE DE 0 C(2&1) C(1&2) 0 C(g&1) C(g&2) C(1&g) C(2&g) 0 ANÁLISIS DISCRIMINANTE 34

Clasificación general para g poblaciones El coste esperado por mala clasificación dado que la observación viene de es: En general, el coste esperado por mala clasificación es: ANÁLISIS DISCRIMINANTE 35

Clasificación general para g poblaciones El CEMC también se puede escribir como: ANÁLISIS DISCRIMINANTE 36

Clasificación general para g poblaciones Teorema El CEMC se minimiza asignando la observación x a la población para la cual Corolario Si todos los costes de clasificación son iguales, el CEMC se minimiza cuando es mínima, es decir, cuando se clasifica x en la población donde es máxima. ANÁLISIS DISCRIMINANTE 37

Clasificación general para g poblaciones La región de puntos que se clasifican en la población i es ANÁLISIS DISCRIMINANTE 38

Clasificación para g poblaciones normales En este caso se conoce la función de densidad para Dada la variable con y las g poblaciones respectivamente, el objetivo es hallar las g regiones R 1, R 2 , . . . , Rg que minimizan el CEMC. ANÁLISIS DISCRIMINANTE 39

Clasificación para g poblaciones normales La función de densidad en el caso normal para las poblaciones es: Si los costes son iguales, hay que maximizar ANÁLISIS DISCRIMINANTE . 40

Clasificación para g poblaciones normales Se clasifica x en es decir, si: si , ANÁLISIS DISCRIMINANTE 41

Clasificación para g poblaciones normales Como las matrices de covarianzas son distintas, se tiene una expresión cuadrática: Score cuadrático de clasificación Se clasifica x en si Nota: Si no hay probabilidades a priori, log pi = 0. ANÁLISIS DISCRIMINANTE 42

Clasificación para g poblaciones normales Versión muestral Sea. y sean g poblaciones conocidas g matrices de datos, de tamaños n 1, n 2, . . . , ng, no necesariamente iguales: ANÁLISIS DISCRIMINANTE 43

Clasificación para g poblaciones normales Versión muestral Sean ANÁLISIS DISCRIMINANTE 44

Clasificación para g poblaciones normales Versión muestral La función de densidad estimada es: El score cuadrático de clasificación es: Se clasifica x en si , es decir, si ANÁLISIS DISCRIMINANTE 45

Clasificación para g poblaciones normales con matrices de covarianzas iguales Score lineal de clasificación Sean Nota: si las matrices de covarianzas son: • Iguales: caso lineal • Distintas: caso cuadrático Si todas las poblaciones tienen distribución normal, el score cuadrático sería: ANÁLISIS DISCRIMINANTE 46

Clasificación para g poblaciones normales con matrices de covarianzas iguales: Score lineal de clasificación Si desarrollando la forma cuadrática llega al score lineal de clasificación. se ANÁLISIS DISCRIMINANTE 47

Clasificación para g poblaciones normales con matrices de covarianzas iguales Score lineal de clasificación Para clasificar, hay que maximizar Score lineal de clasificación La regla de clasificación por tanto, es clasificar x en si ANÁLISIS DISCRIMINANTE 48

Clasificación para g poblaciones normales con matrices de covarianzas iguales Versión muestral Sea la variable con distribuciones estimadas y las g poblaciones respectivamente. Si se estima con Si=S, el score lineal de clasificación queda Score lineal muestral de clasificación ANÁLISIS DISCRIMINANTE 49

Clasificación para g poblaciones normales con matrices de covarianzas iguales Versión muestral La regla de clasificación es asignar x a si es el estimador de la media y S es el estimador de : ANÁLISIS DISCRIMINANTE 50