SIMULACION DE SISTEMAS DISCRETOS Generacin de nmeros pseudoaleatorios






























- Slides: 41

SIMULACION DE SISTEMAS DISCRETOS Generación de números pseudoaleatorios Mg. Samuel Oporto Díaz

Objetivo de la Sesión • Exponer los métodos de generación de números aleatorios. 2 /41

Tabla de Contenido 1. 2. 3. 4. Mapa Conceptual Generación de Series de Números Aleatorios. Generadores no congruenciales Generadores congruenciales 3 /41

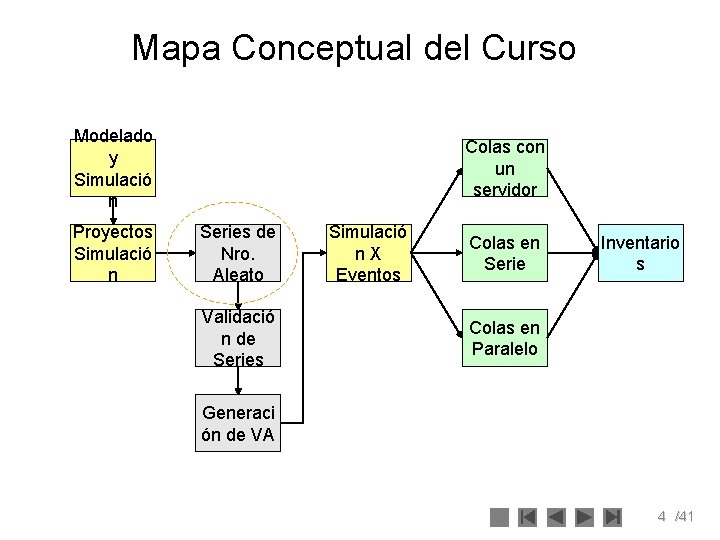
Mapa Conceptual del Curso Modelado y Simulació n Proyectos Simulació n Colas con un servidor Series de Nro. Aleato Validació n de Series Simulació n X Eventos Colas en Serie Inventario s Colas en Paralelo Generaci ón de VA 4 /41

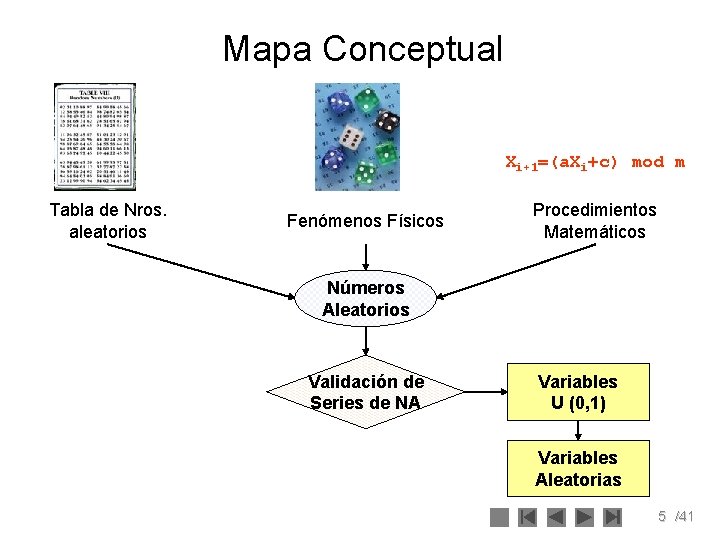
Mapa Conceptual Xi+1=(a. Xi+c) mod m Tabla de Nros. aleatorios Fenómenos Físicos Procedimientos Matemáticos Números Aleatorios Validación de Series de NA Variables U (0, 1) Variables Aleatorias 5 /41

GENERACIÓN DE SERIES DE NÚMEROS ALEATORIOS 6 /41

Generación de Números Aleatorios • Rol preponderante en el proceso de simulación. • Para simular necesitamos de números aleatorios como semillas para generar muestras de V. A. • Características de un generador de nros aleatorios: • 1) Muestrea valores de Distribución Uniforme. • 2) Asegura la NO Correlación Serial. 7 /41

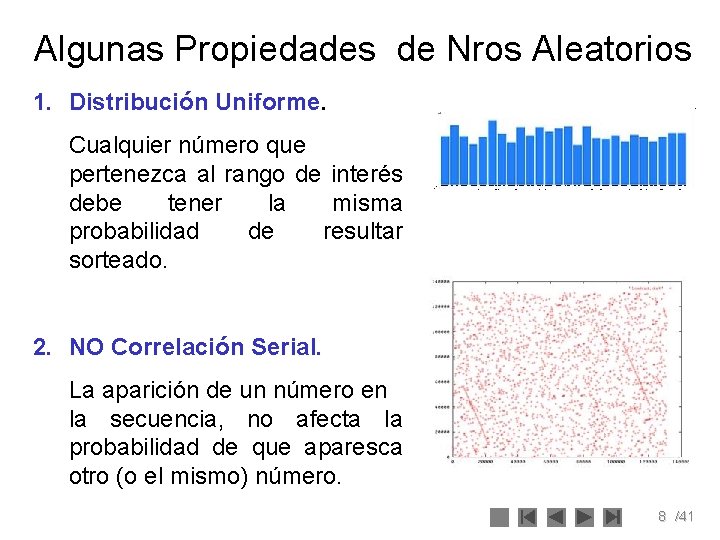
Algunas Propiedades de Nros Aleatorios 1. Distribución Uniforme. Cualquier número que pertenezca al rango de interés debe tener la misma probabilidad de resultar sorteado. 2. NO Correlación Serial. La aparición de un número en la secuencia, no afecta la probabilidad de que aparesca otro (o el mismo) número. 8 /41

Ejemplo La sucesión 1, 2, 3, 4, 5, 1, 2, 3, 4, 5. . . es uniforme pero está correlacionada. Existen Tests que verifican las condiciones de uniformidad y correlación serial, temas que veremos mas adelante. 9 /41

Series de números aleatorios • No tiene sentido el concepto de “número aleatorios”. • Se usa el concepto de “serie de números aleatorios” • “Una sucesión de números es aleatoria si no puede reproducirse eficientemente mediante un programa más corto que la propia seria” • “Una sucesión de números es aleatoria si nadie que utilice recursos computacionales razonables en tiempo razonable puede distinguir entre la serie y una sucesión verdaderamente aleatoria de una forma mejor que tirando una moneda fiel para decidir cuál es cuál” Definiciones provenientes de la teoría computacional

Serie de Números Aleatorios • Son números que deben de cumplir los requisitos de espacio equiprobable, es decir, que todo elemento tenga la misma probabilidad de ser elegido y que la elección de uno no dependa de la elección del otro. 11 /41

Propiedades deseables 1. Uniformemente distribuidos. 2. Estadísticamente independientes (no correlación). 3. Periodo largo (sin repetición). 4. Reproducibles y mutables. 5. Sencillo en su implementación. 6. Portabilidad. 7. Método rápido de generación. 8. Poca memoria para la generación. 12 /41

Mecanismos de generación • Tablas de números aleatorios – RAND (1955), 100, 000 números aleatorios (ruido electrónico) • Fenómenos físicos – Ruido blanco producido por circuitos electrónicos – Recuento de partículas emitidas – Lanzamiento de monedas – Rueda de la fortuna • Procedimientos matemáticos 1. Uniformemente distribuidos. 2. Estadísticamente independientes. 3. Periodo largo (sin repetición). 4. Reproducibles y mutables. 5. Sencillo en su implementación. 6. Portabilidad. – Se usa algoritmos para la generación de números aparentemente aleatorios, se entrega 7. una semilla y se generan los sucesores 8. mediante una función Método rápido de generación. Poca memoria para la generación. 13 /41

Generación de Series de # Aleatorios • Es un proceso fundamental en la simulación. • ¿Por qué? • Para simular el comportamiento de variables aleatorias. – El comportamiento de un sistema depende del comportamiento de sus variables (variables aleatorias). • ¿Qué sucede si en un modelo en lugar de usar una distribución Normal usamos una Poisson? 14 /41

GENERADORES NO CONGRUENCIALES 15 /41

Método del cuadrado medio • Fue propuesto inicialmente por Von Newman y Metrópolis en el año 1946. • Para generar el siguiente número pseudo-aleatorio, se toman los n dígitos centrales del cuadrado del número anterior de n dígitos. • Se requiere una semilla. 16 /41

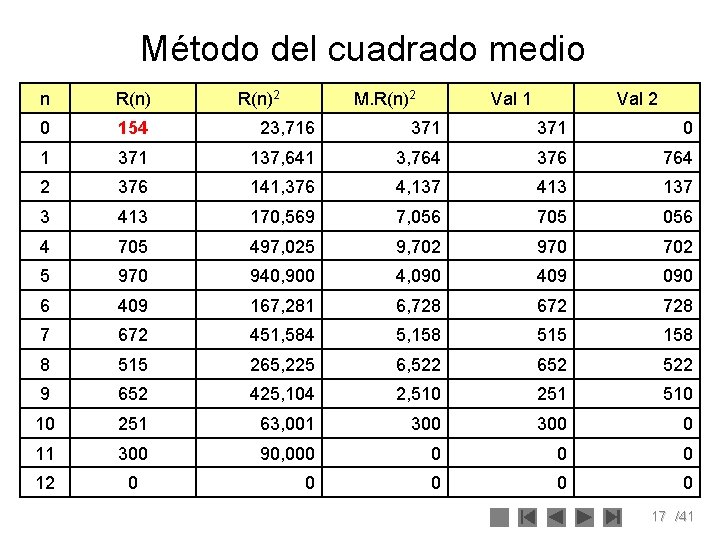
Método del cuadrado medio n R(n)2 M. R(n)2 Val 1 Val 2 0 154 23, 716 371 0 1 371 137, 641 3, 764 376 764 2 376 141, 376 4, 137 413 137 3 413 170, 569 7, 056 705 056 4 705 497, 025 9, 702 970 702 5 970 940, 900 4, 090 409 090 6 409 167, 281 6, 728 672 728 7 672 451, 584 5, 158 515 158 8 515 265, 225 6, 522 652 522 9 652 425, 104 2, 510 251 510 10 251 63, 001 300 0 11 300 90, 000 0 12 0 0 0 17 /41

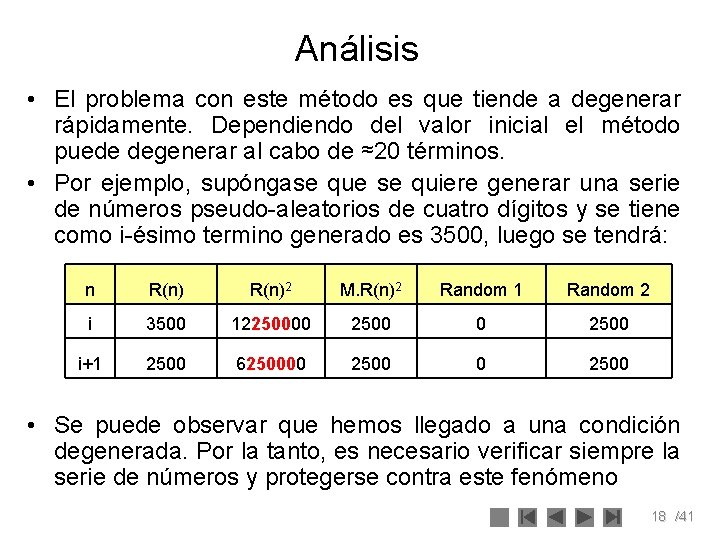
Análisis • El problema con este método es que tiende a degenerar rápidamente. Dependiendo del valor inicial el método puede degenerar al cabo de ≈20 términos. • Por ejemplo, supóngase que se quiere generar una serie de números pseudo-aleatorios de cuatro dígitos y se tiene como i-ésimo termino generado es 3500, luego se tendrá: n R(n)2 M. R(n)2 Random 1 Random 2 i 3500 12250000 2500 i+1 2500 6250000 2500 • Se puede observar que hemos llegado a una condición degenerada. Por la tanto, es necesario verificar siempre la serie de números y protegerse contra este fenómeno 18 /41

Método del Producto Medio • Este método es muy similar al anterior ya que se tomará como número aleatorio siguiente de la serie, a los n dígitos centrales del resultado de una multiplicación previa. • Se requiere dos semillas. 19 /41

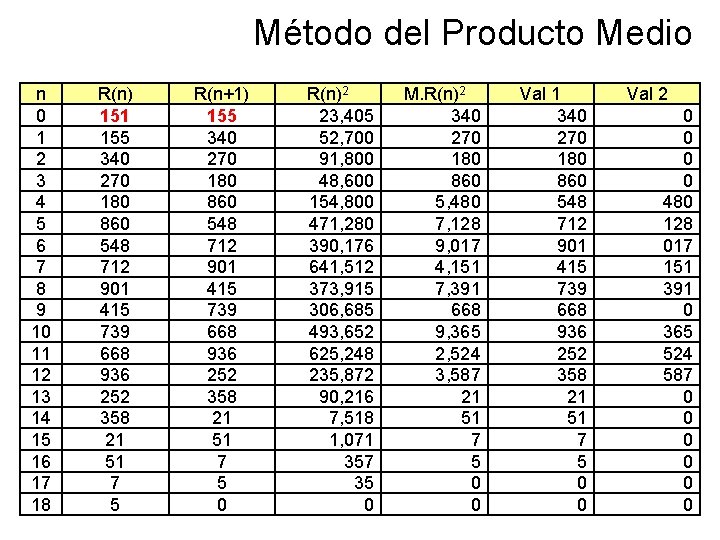
Método del Producto Medio n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 R(n) 151 155 340 270 180 860 548 712 901 415 739 668 936 252 358 21 51 7 5 R(n+1) 155 340 270 180 860 548 712 901 415 739 668 936 252 358 21 51 7 5 0 R(n)2 23, 405 52, 700 91, 800 48, 600 154, 800 471, 280 390, 176 641, 512 373, 915 306, 685 493, 652 625, 248 235, 872 90, 216 7, 518 1, 071 357 35 0 M. R(n)2 340 270 180 860 5, 480 7, 128 9, 017 4, 151 7, 391 668 9, 365 2, 524 3, 587 21 51 7 5 0 0 Val 1 340 270 180 860 548 712 901 415 739 668 936 252 358 21 51 7 5 0 0 Val 2 0 0 480 128 017 151 391 0 365 524 587 0 0 0

Análisis • Una modificación para este método consiste en utilizar un multiplicador constante, en lugar de dos números aleatorios como se muestra a continuación: Rn+1 = K * Rn • Estos métodos son similares al cuadrado medio. • Sin embargo los dos tienen periodos más extensos y los números parecen estar distribuidos uniformemente. • Este método tiende a degenerar a un valor constante. • Tanto el método de cuadrados medios como el de producto medio tienen un periodo corto para la cantidad de números aleatorios que vamos a necesitaremos generar en cada uno de nuestros Modelos. 21 /41

GENERADORES CONGRUENCIALES 22 /41

Generadores Congruenciales • Congruencial Lineal (Mixto). • Congruencial Multiplicativo. 23 /41

Método Congruencial Lineal (MCL) • Los generadores congruenciales lineales generan una serie de números pseudo - aleatorios de tal forma que se puede generar el siguiente a partir del ultimo número derivado, es decir, que el número Xn+1 es generado a partir de Xn. • La relación de recurrencia para el método congruencial mixto es: Xn+1 = (a. Xn + c) mod m Donde: X 0 a c m = semilla (X 0 >0) = multiplicador (a >0) = constante aditiva (c >0) = módulo (m >X 0, m >a y m>c) 24 /41

Método Congruencial Lineal (MCL) • Si se quiere obtener números Uniformes (0, 1) se normaliza el resultado: Un = X n / m • En el MCL, si se repite un número ya se repite toda la secuencia. • Ventajas: 1. utiliza poca memoria y es muy rápido. 2. fácil de volver a generar la misma secuencia, guardando un solo número, (se alcanza con partir desde la misma semilla: X 0). 25 /41

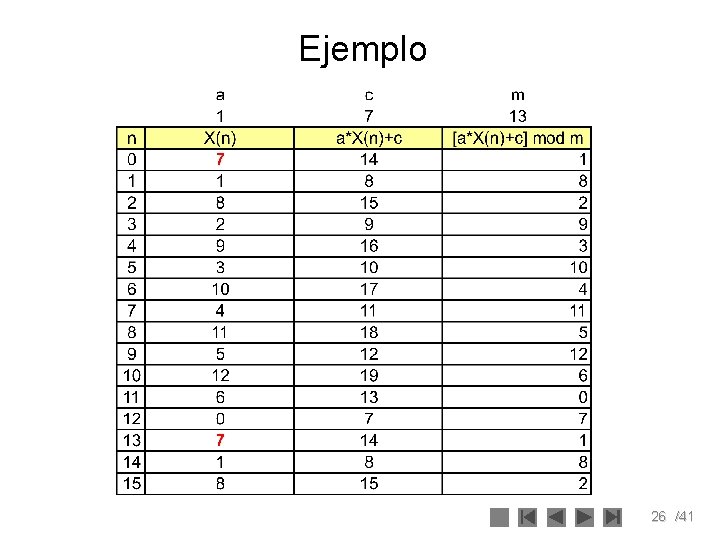
Ejemplo 26 /41

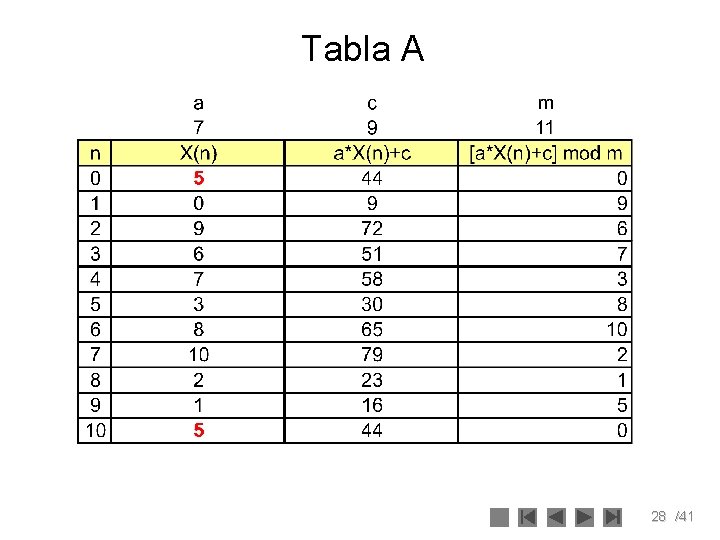
Análisis • Si no se escogen los valores adecuados de los parámetros el período del generador de números pseudo – aleatorios, será menor que m. • En la Tabla A se muestra los valores obtenidos para un generador con parámetros: a = 7, c = 9, X 0 = 5 y m = 11. Como puede apreciarse en la tabla el período del generador es 10 que es menor que el módulo que es 11. • Si bien este caso no es crítico si lo es el que se presenta en la Tabla B donde los parámetros toman los valores de a = X 0 = c = 7 y m=10 cuyo período es de 4, que es un caso muy critico que nos puede llevar a resultados no deseables y poco confiables 27 /41

Tabla A 28 /41

Tabla B 29 /41

Selección de m, a, c, X 0 a) Selección de módulo (m). Existen dos opciones que son las siguientes: a. 1) Escoger al azar el módulo m. a. 2) Tomar m de tal manera que sea el número primo más grande posible y además que sea menor que pd-1, donde p es la base del sistema que se esta usando y d es el número de bits que tiene una palabra de computadora en el sistema que se esta usando. Por ejemplo una computadora XT que trabaja en el sistema binario entonces se tiene que p = 2 y d = 16. 30 /41

Selección de m, a, c, X 0 b) Selección de a. • El valor de a debe ser un número entero impar, que no deberá ser divisible por 3 ó 5. Pero además, para asegurarnos que el generador tenga período completo, el valor que se tome para a deberá escogerse según el siguiente criterio: (a-1) mod 4 = 0 si 4 es un factor de m. (a-1) mod b = 0 si b es un factor primo de m. • Generalmente se toma a igual a 2 k + 1 cuando se trabaja en el sistema binario. En ambos casos el valor que se asigne a k deberá ser mayor o igual que 2. 31 /41

Selección de m, a, c, X 0 c) Selección de c. • Este parámetro puede tomar cualquier valor. Pero para asegurarnos de tener buenos resultados se deberá seleccionar según la siguiente regla: c mod 8 = 5 • En consecuencia c deberá tomar un valor entero impar y relativamente primo a m. 32 /41

Selección de m, a, c, X 0 d) Selección de X 0 • Se tiene que para el generador congruencial el valor que tome X 0 es irrelevante y tiene poca o ninguna influencia sobre las propiedades estadísticas de las series de números pseudo - aleatorios que se generen. 33 /41

Método Congruencial Lineal (MCL) • Para terminar esta parte se debe señalar que existen otras formas matemáticas de representar este generador, que son las siguientes: Xn = [an. X 0 + c{(an - 1)/(a - 1)}] mod m Xn+k =[an. Xk + c{(an - 1)/(a - 1)}] mod m 34 /41

Método Congruencial Multiplicativo • En forma semejante al método anterior el generador congruencial multiplicativo genera el próximo número pseudo - aleatorio a partir del último número calculado, siguiendo la siguiente relación de recurrencia: Xn+1 = a. Xnmod m • Para este generador también se deben escoger adecuadamente los valores de a, X 0, y m, con la finalidad de que se pueda asegurar un período máximo para la series pseudo - aleatorias generadas por este método. A continuación se dan las reglas que indican como se deben escoger estos valores. 35 /41

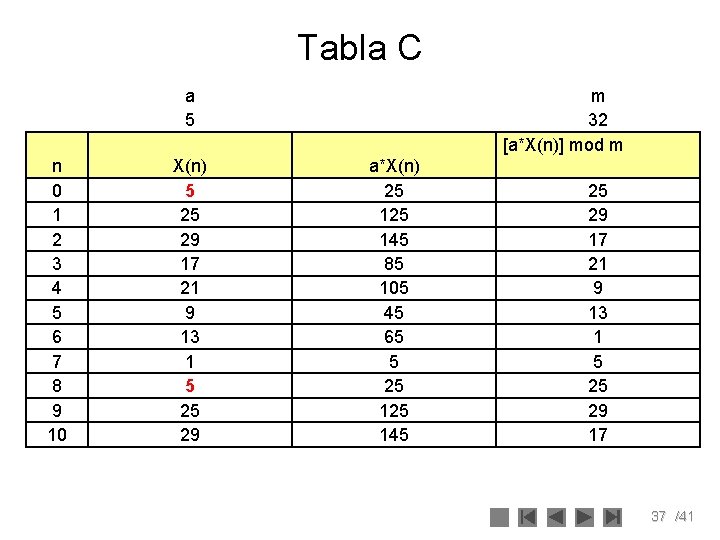
Selección de m, a, X 0 • Para trabajar en el sistema binario los valores de los parámetros deberán escogerse siguiendo las siguientes reglas: – El valor de X 0 debe ser un número entero impar y relativamente primo a m. – El valor de a debe ser obtenido a partir de la siguiente expresión: a = 8 t ± 3 Donde t es cualquier entero. – El valor de m puede ser 2 d. • Si m = 2 d el período del generador es 2 d-2 ó m/4. • A modo de ejemplo se obtendremos el período de un generador cuyos parámetros son: a = 5, X 0 = 5 y m = 32. En la siguiente tabla se muestra los elementos que componen la serie generada cuyo período es de 8 36 /41

Tabla C a 5 n 0 1 2 3 4 5 6 7 8 9 10 X(n) 5 25 29 17 21 9 13 1 5 25 29 m 32 [a*X(n)] mod m a*X(n) 25 145 85 105 45 65 5 25 145 25 29 17 21 9 13 1 5 25 29 17 37 /41

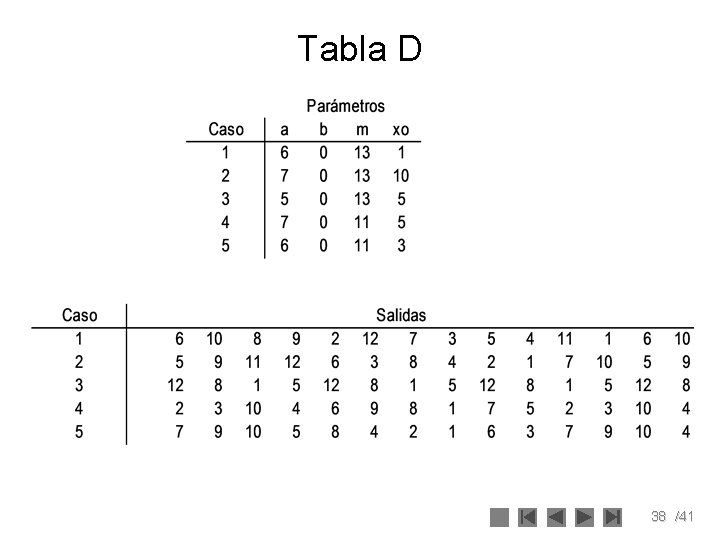
Tabla D 38 /41

Streams - Torrentes • Un generador de números aleatorios que comience con la misma semilla, siempre producirá la misma torrente o secuencia de números. • Diferentes semillas generarán diferentes secuencias. Si las semillas se eligen con valores no cercanos (en el ciclo del generador), entonces las secuencias de números generados (torrentes) parecerán y actuarán como números aleatorios independientes entre sí con lo que colaborarán en la generación de v. a. Independientes entre sí. 39 /41

Tarea 5 • Implementar en Excel estos 4 generadores y probar los métodos de selección. 40 /41

PREGUNTAS 41 /41
 Jorge guillen movimiento literario
Jorge guillen movimiento literario Generacion del 27 contexto historico
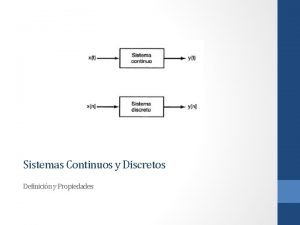
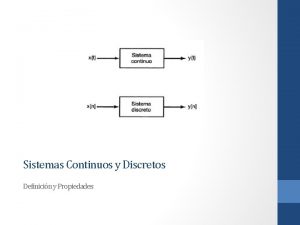
Generacion del 27 contexto historico Continuo discreto
Continuo discreto Ejemplos de sistemas continuos y discretos
Ejemplos de sistemas continuos y discretos Simulacion en proteus
Simulacion en proteus Simulador extend
Simulador extend Desventajas del software arena
Desventajas del software arena Simulación de procesos
Simulación de procesos Metodo de composicion simulacion
Metodo de composicion simulacion Simulacion en administracion
Simulacion en administracion Arturo cassinelli
Arturo cassinelli Distribucion binomial excel
Distribucion binomial excel Numeros romanos ejercitacion
Numeros romanos ejercitacion Numeros romanos
Numeros romanos Numeral cardinal
Numeral cardinal Nmeros reales
Nmeros reales Nmeros naturales
Nmeros naturales Nmeros ordinales
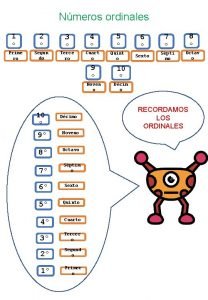
Nmeros ordinales Nmeros enteros
Nmeros enteros Nmeros enteros
Nmeros enteros Nmeros
Nmeros Nmeros ordinales
Nmeros ordinales Nmeros naturales
Nmeros naturales Numero romano ivx
Numero romano ivx Temporalidad de los romanos
Temporalidad de los romanos Número divisivel por 7
Número divisivel por 7 Nmeros naturales
Nmeros naturales Primero segundo tercero cuarto y quinto
Primero segundo tercero cuarto y quinto Recta numerica de numeros enteros
Recta numerica de numeros enteros Nmeros enteros
Nmeros enteros Yu chi ho
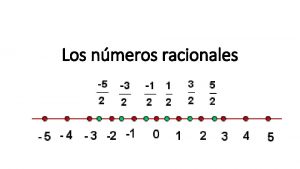
Yu chi ho Nmeros reales
Nmeros reales Nyuexternal
Nyuexternal Nmeros ordinales
Nmeros ordinales Modelos discretos
Modelos discretos Logaritmos discretos
Logaritmos discretos Eventos discretos ejemplos
Eventos discretos ejemplos Que son datos discretos y continuos
Que son datos discretos y continuos Datos continuos
Datos continuos Sistemas controlados por sucesos
Sistemas controlados por sucesos Escalerizacion de sistemas
Escalerizacion de sistemas Buses del sistema
Buses del sistema