Sistemas Continuos y Discretos Definicin y Propiedades Sistemas

Sistemas Continuos y Discretos Definición y Propiedades

Sistemas Continuos y Discretos •

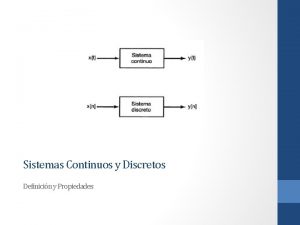
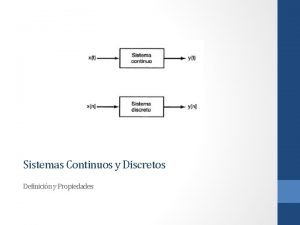
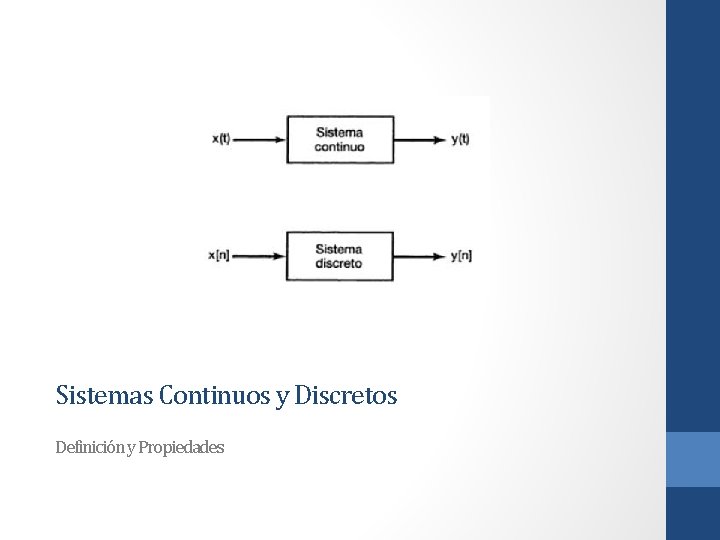
Sistemas Continuos y Discretos Un sistema continuo es aquel en el cual las señales continuas de entrada son transformadas en señales continuas de salida. Tales sistemas serán representados gráficamente como en la figura 1. 41(a), donde x(t) es la entrada y y(t) es la salida. En forma alterna, con frecuencia representaremos la relación entrada-salida de un sistema continuo mediante la notación De manera semejante, un sistema discreto, esto es, uno que transforma entradas de tiempo discreto en salidas de tiempo discreto, se ilustrará como se muestra en la figura 1. 41(b) y será representado simbólicamente como

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos Al examinar y comparar las ecuaciones (1. 82) y (1. 84) en los ejemplos anteriores, vemos que las relaciones entrada-salida "capturadas" en estas dos ecuaciones, para estos dos sistemas físicos muy diferentes, son básicamente las mismas. En particular, ambos ejemplos corresponden a ecuaciones diferenciales lineales de primer orden. de la forma donde x(t) es la entrada, y(t) es la salida y b son constantes. Este es un ejemplo muy sencillo del hecho de que, si desarrollamos métodos para analizar clases generales de sistemas como las representadas mediante la ecuación (1. 85), seremos capaces de usarlos en una amplia variedad de aplicaciones. Cualquier modelo usado para describir o analizar un sistema físico representa una idealización de dicho sistema, y por ello cualquier análisis que resulte será sólo tan bueno como el modelo mismo. Por ejemplo, el modelo lineal simple de un resistor en la ecuación (1. 80) y el de un capacitar en la ecuación (1. 81) son idealizaciones. No obstante, estas idealizaciones son bastante precisas para resistores y capacitores reales en muchas aplicaciones, y así, el análisis que hace uso de dichas idealizaciones proporciona resultados y conclusiones útiles, siempre y cuando los voltajes y corrientes se mantengan dentro de las condiciones de operación bajo las cuales estos modelos lineales simples sean válidos. En este curso se desarrollarán herramientas para analizar una clase particular de sistemas conocida como sistemas lineales e invariante en el tiempo.

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos Interconexiones de sistemas Muchos sistemas reales están construidos como interconexiones de varios subsistemas. Viendo estos sistemas como una interconexión de sus componentes, podemos usar nuestro conocimiento de los sistemas de componentes y la forma en que están interconectados con el fin de analizar la operación y comportamiento del sistema completo. Además, al describir un sistema en términos de una interconexión de subsistemas más simples, podremos, de hecho, ser capaces de definir métodos útiles para sintetizar sistemas complejos a partir de bloques fundamentales básicos más simples. Una interconexión en serie o en cascada de dos sistemas se ilustra en la figura 1. 42(a). Los diagramas como éste se conocen como diagramas de bloque. Aquí la salida del sistema 1 es la entrada del sistema 2, y el sistema completo transforma una entrada al procesarla primero por el sistema 1 y posteriormente por el sistema 2. Un ejemplo de una interconexión en serie es un receptor de radio seguido par un amplificador. De manera similar, se puede definir una interconexión en serie de tres o más sistemas. En la figura 1. 42(b) se ilustra una interconexión en paralelo de dos sistemas. En éste, la misma señal de entrada se aplica a los sistemas 1 y 2. El símbolo “� ” en la figura denota adición, de manera que la salida de la interconexión en paralelo es la suma de las salidas de los sistemas 1 y 2. Un ejemplo de una interconexión en paralelo es un sistema simple de audio con varios micrófonos que alimentan a un solo sistema de amplificador y bocina. Además de la interconexión en paralelo sencilla de la figura 1 . 42(b), se pueden definir interconexiones de dos o más sistemas, y podemos combinar ambas interconexiones, cascada y paralelo, para obtener una interconexión más complicada. Un ejemplo de este tipo de interconexión se muestra en la figura 1. 42(c).

Sistemas Continuos y Discretos

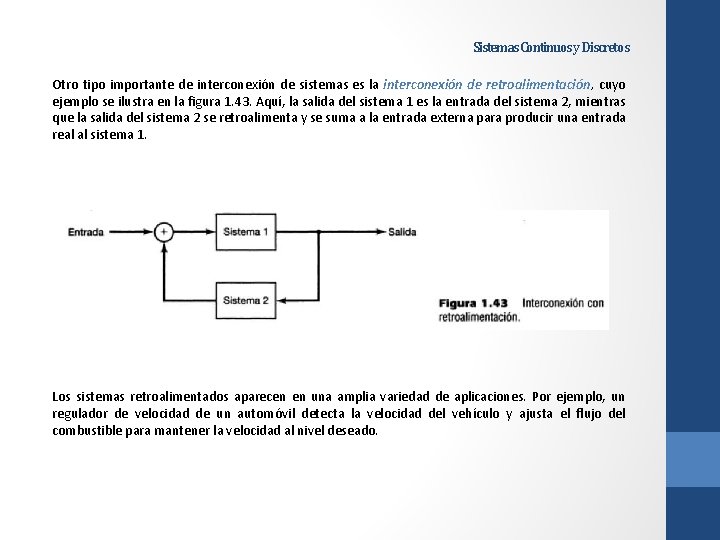
Sistemas Continuos y Discretos Otro tipo importante de interconexión de sistemas es la interconexión de retroalimentación, cuyo ejemplo se ilustra en la figura 1. 43. Aquí, la salida del sistema 1 es la entrada del sistema 2, mientras que la salida del sistema 2 se retroalimenta y se suma a la entrada externa para producir una entrada real al sistema 1. Los sistemas retroalimentados aparecen en una amplia variedad de aplicaciones. Por ejemplo, un regulador de velocidad de un automóvil detecta la velocidad del vehículo y ajusta el flujo del combustible para mantener la velocidad al nivel deseado.

Sistemas Continuos y Discretos Los circuitos eléctricos con frecuencia también son vistos en forma útil como si tuvieran varias interconexiones retroalimentadas. Como un ejemplo, considere el circuito representado en la figura 1. 44(a). Como se indica en la figura 1. 44(b), este sistema se puede ver como la interconexión retroalimentada de los dos elementos del circuito.

Sistemas Continuos y Discretos •

Sistemas Continuos y Discretos De manera similar, un resistor es un sistema sin memoria; con la entrada x(t) tomada como la corriente y considerando el voltaje como la salida y(t), la relación entrada-salida de un resistor es donde R es la resistencia. Un sistema sin memoria particularmente simple es el sistema de identidad, cuya salida es idéntica a su entrada, Es decir, la relación entrada-salida para el sistema de identidad continuo es y la versión discreta correspondiente es Un ejemplo de un sistema discreto con memoria es un acumulador o sumador

Sistemas Continuos y Discretos Un segundo ejemplo de sistema con memoria es un retraso Un capacitor es un ejemplo de un sistema continuo con memoria, ya que si la entrada se toma como la corriente y la salida como el voltaje, entonces donde C es la capacitancia. De forma general, el concepto de memoria en un sistema corresponde a la presencia de un mecanismo en el sistema que mantiene o almacena información sobre los valores de entrada en instantes diferentes del tiempo actual. Por ejemplo, el retraso en la ecuación (1. 93) debe mantener o almacenar el valor precedente de la entrada. De manera similar, el acumulador de la ecuación (1. 92) debe “recordar" o almacenar información acerca de las entradas pasadas. El acumulador, en particular, calcula la suma consecutiva de todas las entradas hasta el momento actual, y entonces, en cada instante de tiempo, el acumulador debe agregar el valor de la entrada actual al valor precedente de la suma consecutiva. En otras palabras, la relación entre la entrada y la salida de un acumulador se puede describir como

Sistemas Continuos y Discretos o, de manera equivalente, Representado en esta última forma, para obtener la salida en el tiempo actual n, el acumulador debe recordar la suma consecutiva de los valores de entrada previos, la cual es exactamente el valor precedente de la salida del acumulador. En muchos sistemas físicos, la memoria está directamente asociada con el almacenamiento de energía. Por ejemplo, el capacitor en la ecuación (1. 94) almacena energía mediante la acumulación de la carga eléctrica, representada como la integral de la corriente. Entonces, el circuito RC sencillo del ejemplo 1. 8 y de la figura 1. 1 tiene memoria almacenada físicamente en el capacitor. De manera semejante, el automóvil de la figura 1. 2 tiene memoria almacenada en su energía cinética. En los sistemas discretos construidos con computadoras o microprocesadores digitales, la memoria está típicamente asociada de forma directa con el almacenamiento de registros que retienen valores entre pulsos de reloj. Mientras que el concepto de memoria en un sistema podría sugerir típicamente el almacenamiento de los valores pasados de la entrada y la salida, nuestra definición formal es que un sistema tiene memoria si la salida actual depende de valores pasados o futuros de la entrada y la salida.

Sistemas Continuos y Discretos Invertibilidad y sistemas inversos Se dice que un sistema es invertible si distintas entradas producen distintas salidas. Como se ilustra en la figura 1. 45(a) para el caso discreto, si un sistema es invertible, entonces existe un sistema inverso tal que, cuando está en cascada con el sistema original, produce una salida w[n] igual a la entrada x[n] del primer sistema. Entonces, la interconexión en serie de la figura 1. 45(a) tiene una relación entrada-salida total que es la misma que la del dsistema de identidad.

Sistemas Continuos y Discretos Un ejemplo de un sistema continuo invertible es para el cual el sistema inverso es Este ejemplo se ilustra en la figura 1. 45(b). Otro ejemplo de un sistema invertible es el acumulador de la ecuación (1. 92). Para este sistema, la diferencia entre dos valores sucesivos de la salida es precisamente el último valor de entrada (valor presente de la entrada). Por tanto, en este caso, el sistema inverso es como se ilustra en la figura 1. 45(c).

Sistemas Continuos y Discretos Ejemplos de sistemas no invertibles son esto es, el sistema que produce la secuencia de salida cero para cualquier secuencia de entrada, y ejemplo en el cual no podemos determinar el signo de la entrada a partir de nuestro conocimiento del signo de la salida. El concepto de invertibilidad es importante en muchos contextos. Un ejemplo surge en los sistemas de codificación utilizados en una amplia variedad de aplicaciones de comunicación. En tales sistemas, una señal que deseamos transmitir primero se aplica como entrada a un sistema conocido como codificador. Hay muchas razones para hacer esto, que van desde el encriptamiento del mensaje original para fines de comunicación segura o privada, hasta proporcionar algo de redundancia en la señal (por ejemplo, agregando lo que es conocido como bits de paridad) de manera que cualquier error que ocurra en la transmisión se puede detectar y, posiblemente, corregir. Para una codificación sin pérdidas, la entrada al codificador debe ser recuperable en forma precisa de la salida; es decir, el codificador debe ser invertible.

Sistemas Continuos y Discretos •

Sistemas Continuos y Discretos Aunque los sistemas causales son de gran importancia, de ninguna manera constituyen los únicos sistemas que resultan de interés práctico. Por ejemplo, la causalidad no es de importancia fundamental en aplicaciones como el procesamiento de imágenes, en el cual la variable independiente no es el tiempo. Más aún, en el procesamiento de datos que han sido grabados previamente, como ocurre con frecuencia con señales de voz, de geofísica o señales meteorológicas, por nombrar algunas, de ninguna manera estamos obligados a procesar esos datos de forma causal. Como otro ejemplo, en muchas aplicaciones, incluyendo el análisis histórico del mercado de valores y los estudios demográficos, podemos estar interesados en determinar una tendencia de variación lenta en datos que también contengan fluctuaciones de alta frecuencia alrededor de esa tendencia. En este caso, una aproximación usada con frecuencia consiste en promediar los datos sobre un intervalo para suavizar las fluctuaciones y mantener solamente la tendencia.

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos Estabilidad La estabilidad es otra importante propiedad de los sistemas. Intuitivamente, un sistema estable es aquel en el que entradas pequeñas conducen a respuestas que no divergen. Por ejemplo, considere el péndulo en la figura 1. 46(a), en el cual la entrada es la fuerza aplicada x(t) y la salida es la desviación angular y(t) a partir de la vertical. En este caso, la gravedad aplica una fuerza de restauración que tiende a regresar el péndulo a la posición vertical, y las pérdidas por fricción debidas al arrastre tienden a disminuir su velocidad. En consecuencia, si se aplica una pequeña fuerza x(t), la desviación resultante de la vertical también es pequeña. En contraste, para el péndulo invertido de la figura 1. 46(b), el efecto de la gravedad es aplicar una fuerza que tiende a incrementar la desviación de la vertical. Así, una pequeña fuerza aplicada conduce a una gran desviación vertical, lo cual ocasiona que el péndulo caiga, a pesar de cualquier fuerza retardante debida a la fricción.

Sistemas Continuos y Discretos El sistema de la figura 1. 46(a) es un ejemplo de un sistema estable, mientras que el de la figura 1. 46(b) es inestable. Los modelos para reacciones en cadena o para crecimiento de población con suministro de alimentación ilimitado y sin depredadores son ejemplos de sistemas inestables, ya que la respuesta de los sistemas crece sin límite en respuesta a pequeñas entradas. Otro ejemplo de un sistema inestable es el modelo para un balance de cuenta bancaria de la ecuación (1. 86), pues si se hace un depósito inicial (es decir, x[0] - una cantidad positiva) y no hay retiros subsecuentes, entonces ese depósito crecerá cada mes sin Iímite, debido al efecto de los pagos de interés. De manera más formal, si la entrada a un sistema estable es limitada (es decir, si su magnitud no crece en forma ilimitada), entonces la salida también debe ser limitada y por tanto, no puede divergir. Por ejemplo, considere la aplicación de una fuerza constante f(t) = F al automóvil de la figura 1. 2 con el vehículo inicialmente en reposo. En este caso la velocidad del auto se incrementa, pero no sin límite, ya que la fuerza de fricción retardante también se incrementa con la velocidad. De hecho, la velocidad continuará incrementándose hasta que la fuerza de fricción esté en balance exacto con la fuerza aplicada; así, según la ecuación (1. 84) vemos que este valor de velocidad terminal V debe satisfacer es decir,

Sistemas Continuos y Discretos Por otro lado, considere el acumulador descrito por la ecuación (1. 92). A diferencia del sistema de la ecuación (1. 104), este sistema suma todos los valores pasados de la entrada, en lugar de sólo un conjunto finito de valores, siendo entonces inestable, debido a que esta suma puede crecer de manera continua incluso si x[n] está limitada. Por ejemplo, si la entrada al acumulador es un escalón unitario u[n], la salida será Esto es, y[0] = 1, y[1] = 2, y[2] = 3, y así sucesivamente, y y[n] crece sin límite.

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos •

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos •

Sistemas Continuos y Discretos •

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos

Sistemas Continuos y Discretos