Clase 1 Nmeros imaginarios Nmeros imaginarios Los nmeros

Clase 1 Números imaginarios

Números imaginarios Los números imaginarios tienen variadas aplicaciones en diferentes campos. En la física se relacionan con el electromagnetismo, la dinámica de fluidos, la mecánica cuántica y el análisis de vibraciones.

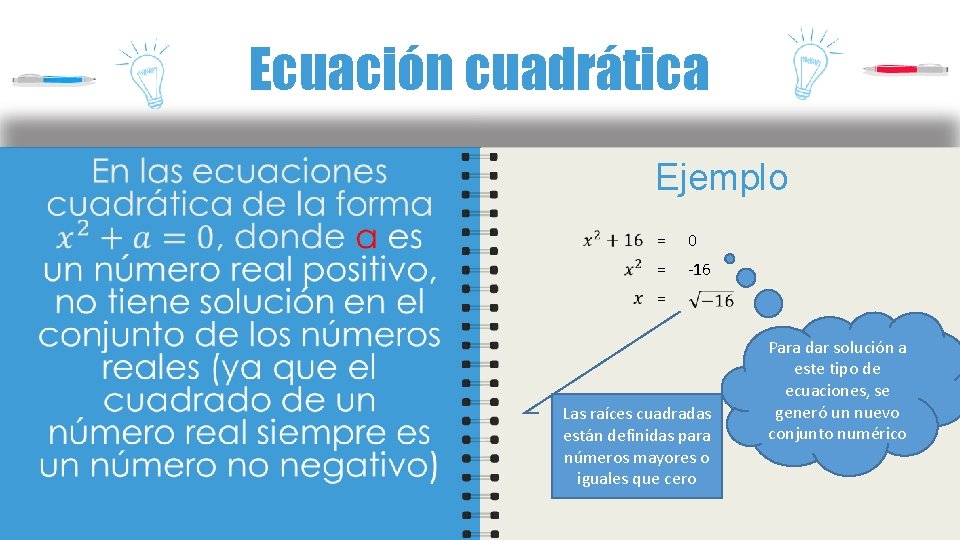
Ecuación cuadrática Ejemplo = 0 = -16 = Las raíces cuadradas están definidas para números mayores o iguales que cero Para dar solución a este tipo de ecuaciones, se generó un nuevo conjunto numérico

Números imaginarios Al escribir la siguientes raíces como números imaginarios puros tenemos: = Se extrae la raíz cuadrada principal de -49 = Se halla la raíz = Se extrae la raíz cuadrada principal de 180 = Se descompone 180 = Se simplifica = Se halla el producto

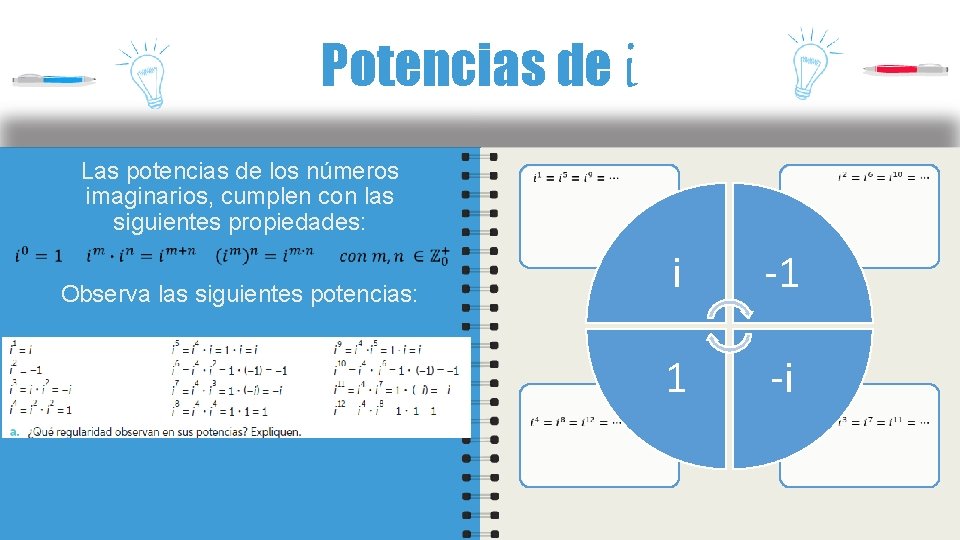
Potencias de i Las potencias de los números imaginarios, cumplen con las siguientes propiedades: • Observa las siguientes potencias: • • i -1 1 -i •

Los “ciclos” son cada 4 Por lo que 16 : 4 = 4 0 (resto) Se calcula el producto Los “ciclos” son cada 4 Por lo que 25 : 4 = 6 1 (resto) producto

Ejemplo En general, para determinar una potencia de i con exponentero, se procede así: • Se expresa el exponente de la forma 4 n + r, donde n es un número entero y r es un número positivo o cero. • Se determina la potencia aplicando las propiedades de las potenciación y las potencias básicas de i Se expresa 23 como 4 n + 1 Se aplican las propiedades de potenciación Se simplifica

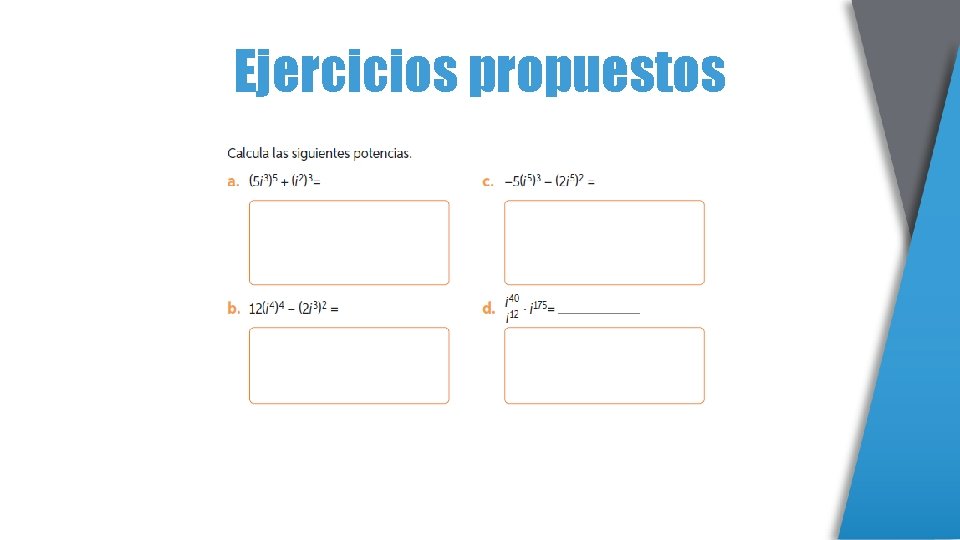
Ejercicios propuestos

Ingresa a classroom Clave 3°A: gn 6 uy 5 q Clave 3°B: fum 73 na Se irá subiendo material y podrás comunicarte conmigo para cualquier duda. Saludos y #quedateencasa