MODELOS DE OPTIMIZACIN RESTRINGIDA Programacin Lineal Programacin lineal

MODELOS DE OPTIMIZACIÓN RESTRINGIDA Programación Lineal

Programación lineal La programación lineal es el planteamiento de modelos en forma numérica y en donde las variables de decisión sobre las cuales se basa el modelo son lineales

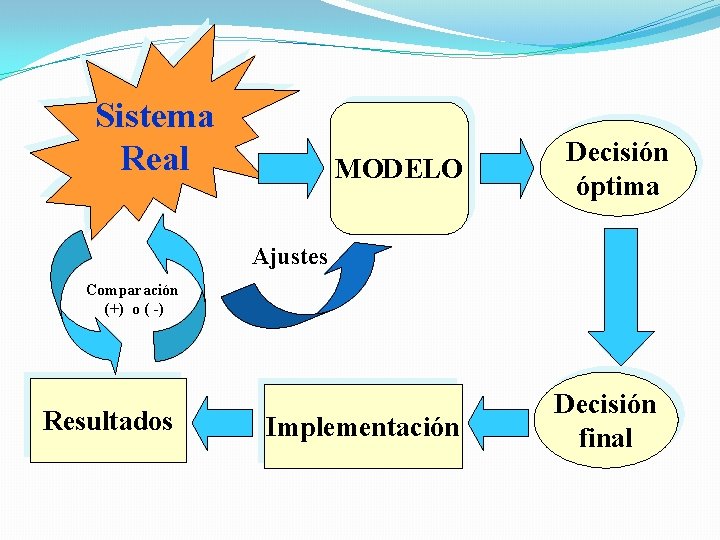
Sistema Real MODELO Decisión óptima Ajustes Comparación (+) o ( -) Resultados Implementación Decisión final

¿Cuál es la estructura del modelo matemático? • Variables de decisión • Parámetros y constantes • Función de optimización: Max/Min • Ecuaciones de restricción

Problema Tecnipolímeros produce 2 líneas de tubo especial flexible, simple y reforzado. La mayor demanda la presenta el tubo simple (E-9) que es utilizado en construcción. El resto de la producción se destina al tubo reforzado (F-9) utilizado en agricultura para riego y transporte de agua. Ambos se producen con el mismo equipo y en el mismo departamento. El gerente de mercadeo asegura que el próximo mes se venderán todos los rollos de E-9 y F-9 que se produzcan. La utilidad por cada E-9 es de Q 5000. 00 y de Q 4000. 00 por cada F-9. Nota: cada rollo mide 2000 metros y se vende para producir rollos mas pequeños

El proceso Primero se realiza el aglomerado de la materia prima y luego su extrusión. Para aglomerarlo hay una disponibilidad de 150 hr. /mes y para la extrusión 160 hr. /mes. Para el E-9 se necesitan 10 hr. de aglomerado y 20 hrs. de extrusión y para el F-9 15 hrs. de aglomerado y 10 de extrusión. Control de calidad, para cumplir con la producción necesita un mínimo de un 10% menos de horas por mes del disponible en aglomerado (150). Para el CC del E-9 se requiere 30 hrs. y cada F-9 10 hrs. La política que se ha mantenido es que por cada E-9 se producen no mas de 3 F-9. Existe un pedido de 5 rollos de cualquier combinación de E-9 y F-9. Optimizar la producción de rollos.

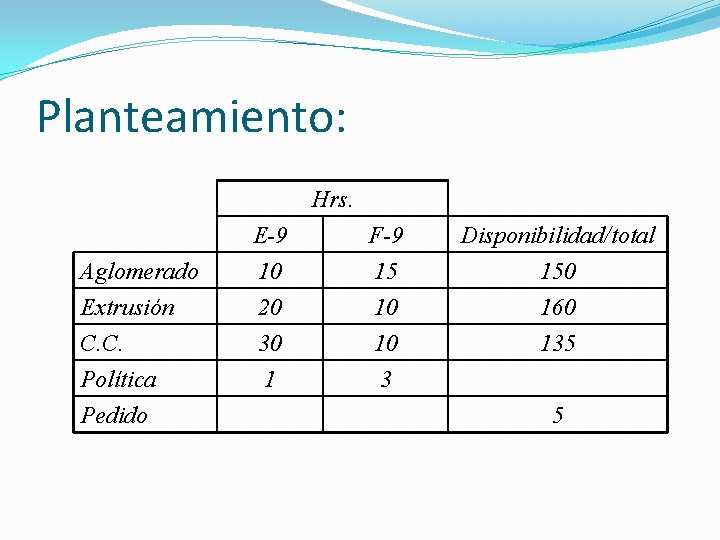
Planteamiento: Hrs. Aglomerado Extrusión C. C. Política Pedido E-9 10 20 F-9 15 10 Disponibilidad/total 150 160 30 1 10 3 135 5

Planteamiento: Si identificamos como E a los rollos de E-9 y como F a los rollos de F-9, podemos expresar las relaciones matemáticamente de la siguiente manera: Restricciones

Planteamiento: Que nos interesa: El interés del problema es la optimización de las utilidades a través de la producción de rollos de poliducto. Es decir, maximizar la suma de utilidades Función Objetivo

Planteamiento matemático: B. R. Restricciones de no negatividad.

Graficación de desigualdades: Una desigualdad es una expresión matemática que contiene un signo mayor que, menor que, mayor o igual que, menor o igual que. Estudiaremos las desigualdades-igualdades que son las que nos interesan, los pasos a seguir son: 1. - Convertir la desigualdad en igualdad y graficar. 2. - Escoger un punto de referencia (cualquier punto que no pertenezca a la recta. 3. - Valuar el punto de ensayo y verificar: a) si el punto satisface la desigualdad todos los puntos de ese lado la satisfacen. b) si no satisfacen la desigualdad entonces todos los puntos que no estén en ese lado la satisfacen.

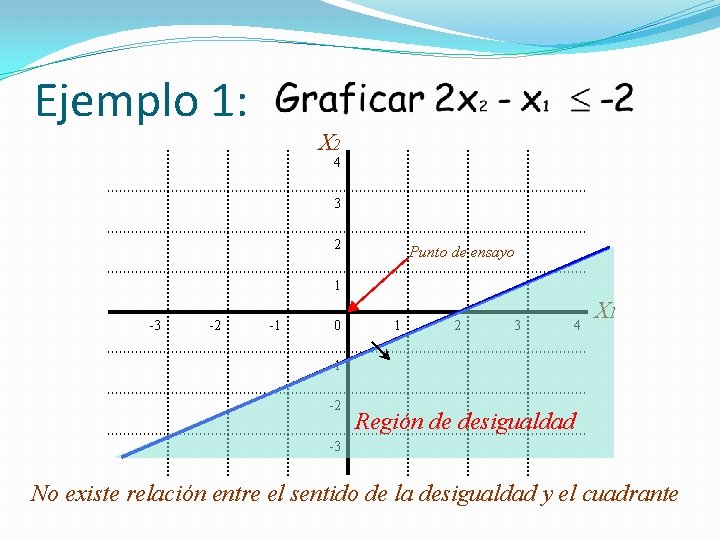
Ejemplo 1: X 2 4 3 2 Punto de ensayo 1 -3 -2 -1 0 1 2 3 4 X 1 -1 -2 Región de desigualdad -3 No existe relación entre el sentido de la desigualdad y el cuadrante

Ejemplo 2: Graficar el siguiente sistema lineal:

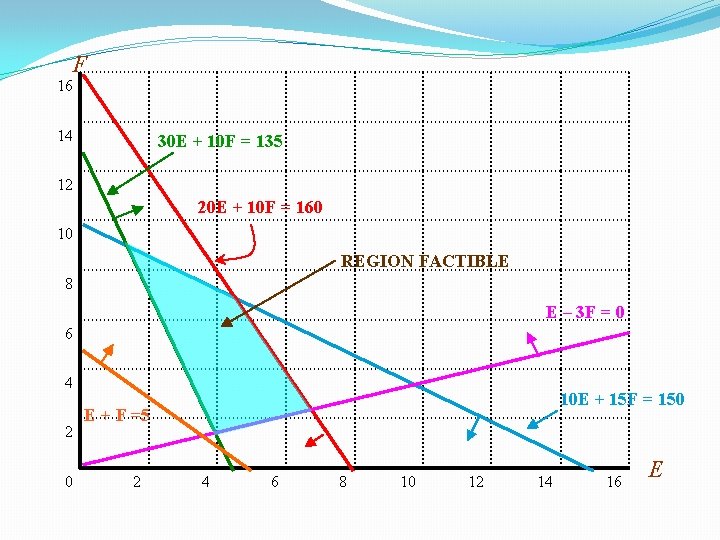
F 16 14 30 E + 10 F = 135 12 20 E + 10 F = 160 10 REGION FACTIBLE 8 E – 3 F = 0 6 4 2 0 10 E + 15 F = 150 E + F =5 2 4 6 8 10 12 14 16 E

Región factible Es el área dentro de la cual se satisfacen todas las restricciones a las que esta sometido el modelo y dentro de la cual se encuentra la solución optima localizada en un vértice. Restricción Redundante Es aquella restricción que al quitarla no hace cambiar la región factible, es decir no se encuentra dentro de la región factible y no conforma un vértice de la misma.

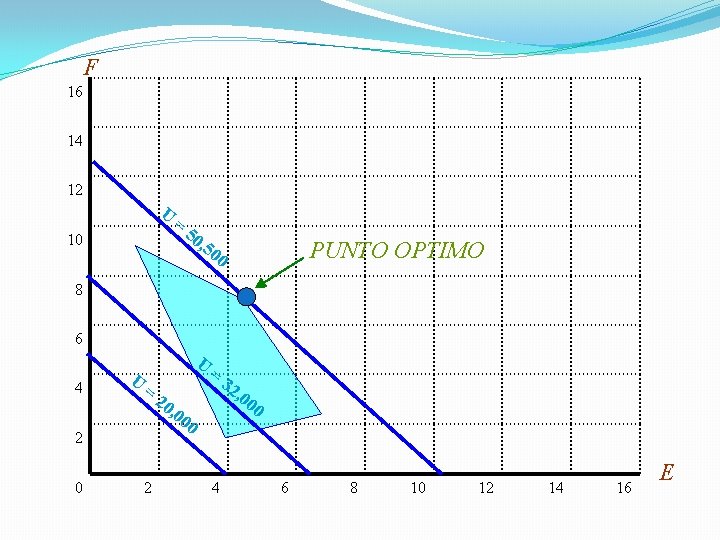
Solución Para encontrar la solución al sistema planteado gráficamente se le dan valores totales aleatorios a la función objetivo y se grafican tratando de que coincidan con algún vértice de la región factible y es en ese vértice en donde se encuentra la solución óptima.

F 16 14 12 U 10 = 50 , 50 PUNTO OPTIMO 0 8 6 4 U U = = , 00 20 0 , 00 0 2 32 4 6 8 10 12 14 16 E

Solución: Como se puede ver que el punto óptimo esta en la intersección de las rectas 10 E + 15 F = 150 20 E + 10 F = 160 y Se despejan las incógnitas ya que se tienen dos ecuaciones con dos incógnitas. Multiplicando la primera por dos y restándole la segunda se tiene: 20 E + 30 F = 300 -20 E - 10 F = -160 20 F = 140 lo que hace que F = 7 y E = 4. 5

Comprobación La solución encontrada debe de satisfacer todas las desigualdades. Substituyendo tenemos los siguiente: E= 4. 5, F = 7 10 (4. 5) + 15(7) = 150 20 (4. 5) + 10(7) = 160 30 (4. 5) + 10(7) = 205 4. 5 - 3(7) = -16. 5 4. 5 + 7 = 11. 5 4. 5, 7 > 0

Definiciones Las desigualdades que en el punto óptimo se vuelven igualdades se conocen como RESTRICCIONES ACTIVAS, y son por las que pasa la solución óptima. 10 (4. 5) + 15(7) = 150 20 (4. 5) + 10(7) = 160 Cuando en el planteamiento de un problema existe una igualdad siempre es activa.

Definiciones Estudiemos la siguiente restricción: Al valuarla en el punto óptimo queda como: 30 (4. 5) + 10(7) = 205 Excedente La diferencia es: 205 – 135 = 70 135 205 Excedente

Definiciones Estudiemos la siguiente restricción: Al valuarla en el punto óptimo queda como: 4. 5 - 3(7) = -16. 5 Holgura La diferencia es: -16. 5 – 0 = -16. 5 0 Holgura

Definiciones Si la restricción es inactiva, para una restricción > o = hay excedente y para una < o = hay holgura. El término solución óptima o punto óptimo se refiere a los valores de las variables de decisión que maximizan o minimizan (según el caso) la función objetivo. El término valor óptimo se refiere al valor de la función objetivo valuada en el punto óptimo. En el planteamiento de un sistema lineal no pueden existir desigualdades exactas, todas son o igualdades o desigualdad.

El problema de la industria de juguetes “Galaxia”. 4 Galaxia produce dos tipos de juguetes: * Space Ray * Zapper 4 Los recursos están limitados a: * 1200 libras de plástico especial. * 40 horas de producción semanalmente.

4 Requerimientos de Marketing. * La producción total no puede exceder de 800 docenas. * El número de docenas de Space Rays no puede exceder al número de docenas de Zappers por más de 450. 4 Requerimientos Tecnológicos. * Space Rays requiere 2 libras de plástico y 3 minutos de producción por docena. * Zappers requiere 1 libra de plástico y 4 minutos de producción por docena.

4 Plan común de producción para: * Fabricar la mayor cantidad del producto que deje mejores ganancias, el cual corresponde a Space Ray ($8 de utilidad por docena). * Usar la menor cantidad de recursos para producir Zappers, porque estos dejan una menor utilidad ($5 de utilidad por docena). 4 El plan común de producción consiste en: Space Rays = 550 docenas Zappers Utilidad = 100 docenas = $4900 por semana

Solución 4 Variables de decisión * X 1 = Cantidad producida de Space Rays (en docenas por semana). * X 2 = Cantidad producida de Zappers (en docenas por semana). 4 Función objetivo * Maximizar la ganancia semanal.

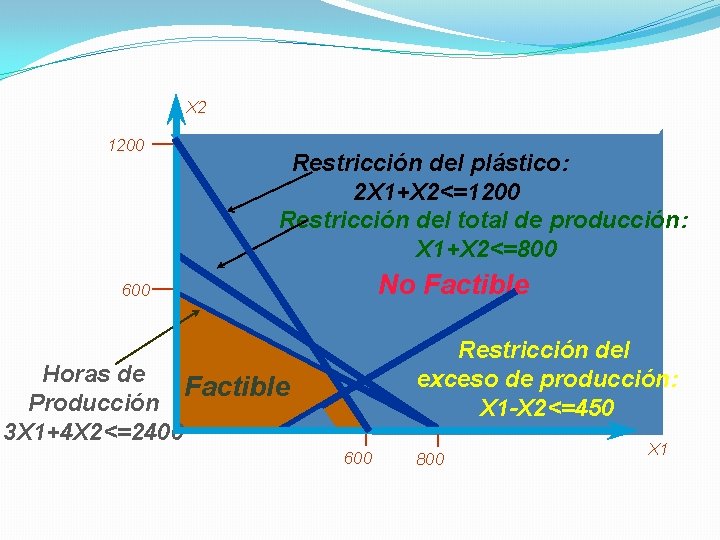
4 Modelo de Programación Lineal Max 8 X 1 + 5 X 2 (ganancia semanal) Sujeto a: 2 X 1 + 1 X 2 <= 1200 (Cantidad de plástico) 3 X 1 + 4 X 2 <= 2400 (Tiempo de producción) X 1 + X 2 <= 800 (Limite producción total) X 1 - X 2 <= 450 (Producción en exceso) Xj >= 0 , j= 1, 2. (Resultados positivos)

X 2 1200 Restricción del plástico: Restricción de plástico 2 X 1+X 2<=1200 Restricción del total de producción: X 1+X 2<=800 No Factible 600 Restricción del exceso de producción: X 1 -X 2<=450 Horas de Factible Producción 3 X 1+4 X 2<=2400 600 800 X 1

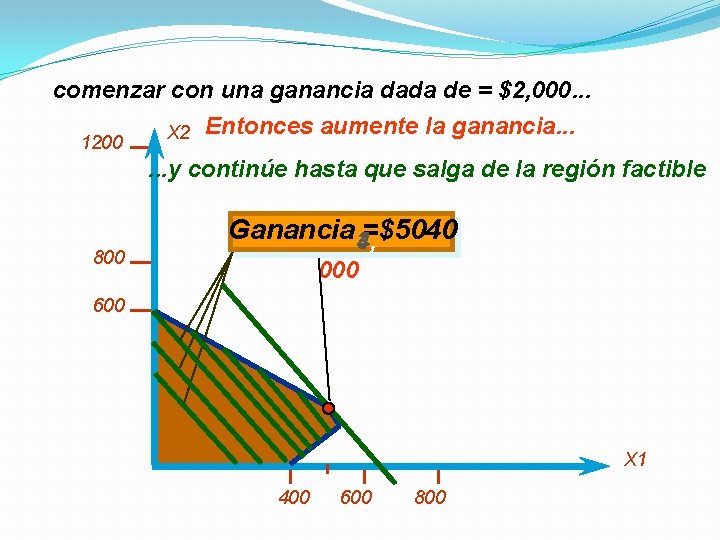
Resolución gráfica para encontrar la solución óptima.

comenzar con una ganancia dada de = $2, 000. . . X 2 Entonces aumente la ganancia. . . 1200 . . . y continúe hasta que salga de la región factible 800 Ganancia Utilid. 3, ==$5040 4, 2, $ 000 600 X 1 400 600 800

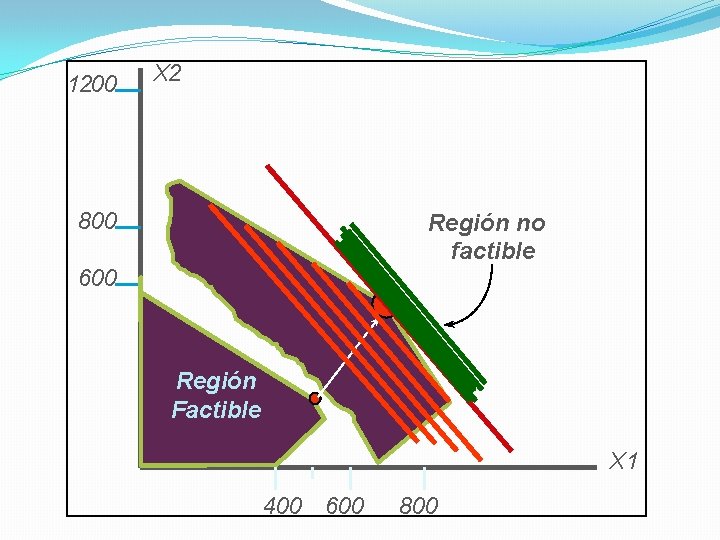
1200 X 2 800 Región no factible 600 Región Factible X 1 400 600 800

4 Resumen de la solución óptima Space Rays = 480 docenas Zappers = 240 docenas Ganancia = $5040 * Esta solución utiliza todas las materias primas (plástico) y todas las horas de producción. * La producción total son 720 docenas (no 800). * La producción de Space Rays excede a la de Zappers por solo 240 docenas y no por 450.

Ejemplo: La empresa Fotográfica S. A. produce dos tipos de líquidos para revelado de fotografías. El primero, un reactivo químico para revelar fotografías en blanco y negro cuya producción cuesta $2, 500. 00 por tonelada. El segundo, un reactivo químico para revelar fotografías en color, cuyo costo es de $3, 000 la tonelada. A partir del análisis de los actuales niveles de inventario y de los pedidos pendientes, el director de producción ha estimado que se deben de producir para el próximo mes al menos 30 ton. , del reactivo para blanco y negro y 20 ton. , del reactivo para color. Además en bodega hay una materia prima altamente perecedera que debe de consumirse en un período de 30 días y que se utiliza en los dos químicos, así que con el fin de consumírsela debe de producir al menos 60 ton. , de ambos reactivos

Ejemplo 2: Si llamamos: X 1 = ton. , producidas del reactivo para blanco y negro X 2 = ton. , producidas del reactivo para colores. Las restricciones nos quedarían así: X 1 ≥ 30 X 2 ≥ 20 X 1 + X 2 ≥ 60

Como en este problema tenemos datos de costo, lo que nos interesa es minimizar ese costo, de tal forma que nuestra función objetivo sería: Minimizar 2, 500 X 1 + 3, 000 X 2

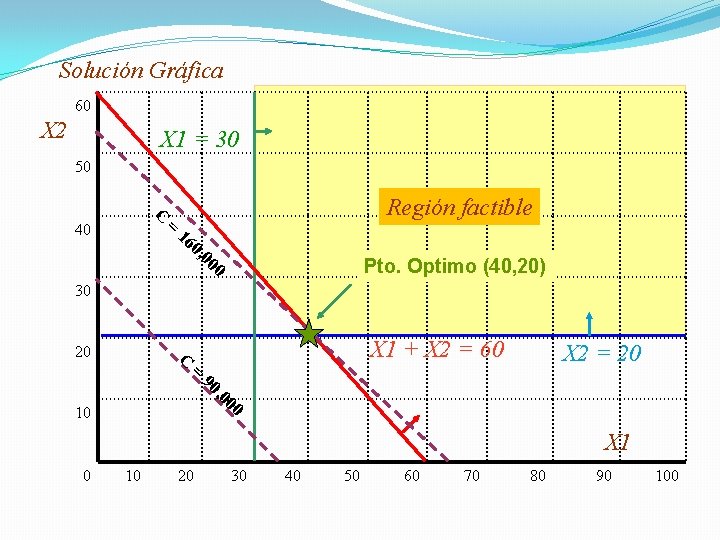
Solución Gráfica 60 X 2 X 1 = 30 50 C 40 = Región factible 16 0, 00 0 Pto. Optimo (40, 20) 30 20 C = X 1 + X 2 = 60 90 , 0 0 10 X 2 = 20 0 X 1 0 10 20 30 40 50 60 70 80 90 100

Ejemplo: Disponemos de 210. 000 euros para invertir en bolsa. Nos recomiendan dos tipos de acciones. Las del tipo A, que rinden el 10% y las del tipo B, que rinden el 8%. Decidimos invertir un máximo de 130. 000 euros en las del tipo A y como mínimo 60. 000 en las del tipo B. Además queremos que la inversión en las del tipo A sea menor que el doble de la inversión en B. ¿Cuál tiene que ser la distribución de la inversión para obtener el máximo interés anual?

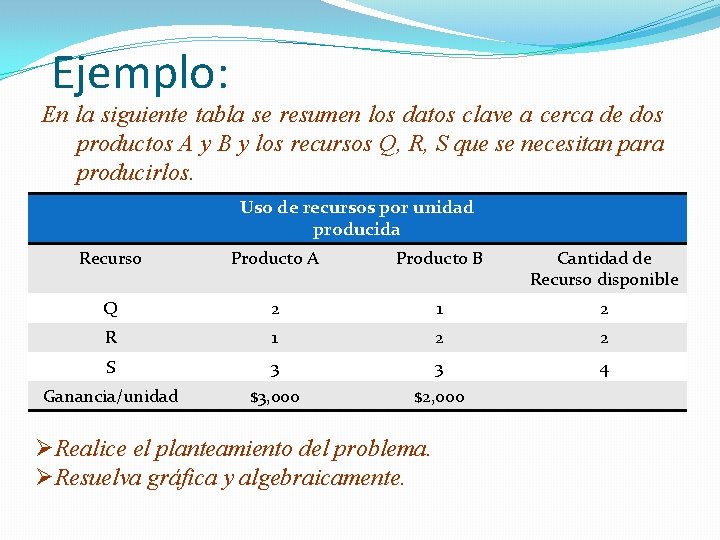
Ejemplo: En la siguiente tabla se resumen los datos clave a cerca de dos productos A y B y los recursos Q, R, S que se necesitan para producirlos. Uso de recursos por unidad producida Recurso Producto A Producto B Cantidad de Recurso disponible Q 2 1 2 R 1 2 2 S 3 3 4 Ganancia/unidad $3, 000 $2, 000 ØRealice el planteamiento del problema. ØResuelva gráfica y algebraicamente.

Ejemplo: Un restaurante prepara comidas para reparto a domicilio. Para este fin de semana 2 locales le han ordenado menús que requieren algún tipo de carne y una ensalada. En ambos menús, el restaurante decide colocar una pieza de carne, sin embargo variará la ensalada de tal forma que para el local A piensa colocar 9 medidas de ensalada por plato y para el local B 14 medidas. Debido a la diferencia de clientes que esta atendiendo el restaurante toma la política de servir el menú del local B en un plato y el del local A en dos. En total el restaurante tiene una existencia de 100 piezas de carne y el equivalente a 1260 medidas de ensalada y platos disponibles para despacho a domicilio tiene 160. Las ganancias por menús son 110 pesetas los del local A y 95 los del local B.