RECTAS Segunda Parte 1 1 CONTENIDO 1 Introduccin

RECTAS Segunda Parte 1 1

CONTENIDO 1. Introducción. 2. Rectas paralelas. 3. Rectas perpendiculares. 4. Sistemas de ecuaciones lineales. Solución método gráfico. Solución método algebraico. Igualación. Sustitución. Eliminación. 5. Generalidades 6. Problemas de aplicación 2

Ecuaciones que representan en el plano cartesiano una recta: General ó estándar Pendiente-ordenada al origen Recta horizontal Punto-pendiente Recta vertical 3

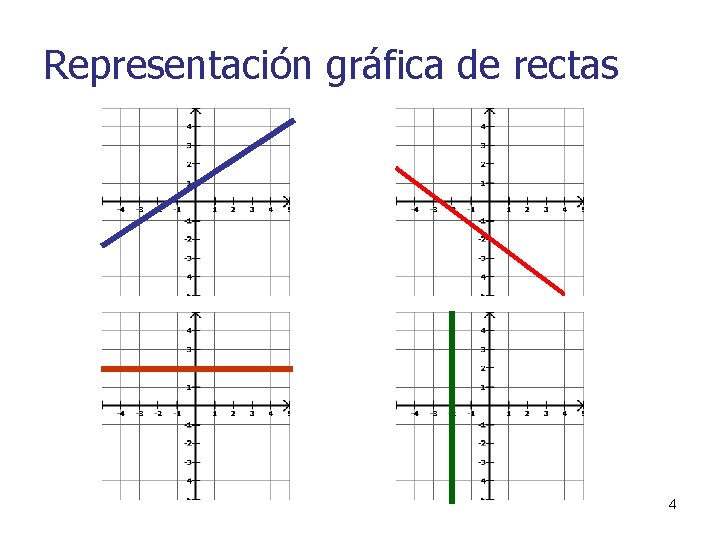
Representación gráfica de rectas 4

PENDIENTE Rectas no verticales Dados puntos cualesquiera en el plano Rectas verticales La pendiente no está definida Rectas horizontales La pendiente es cero 5

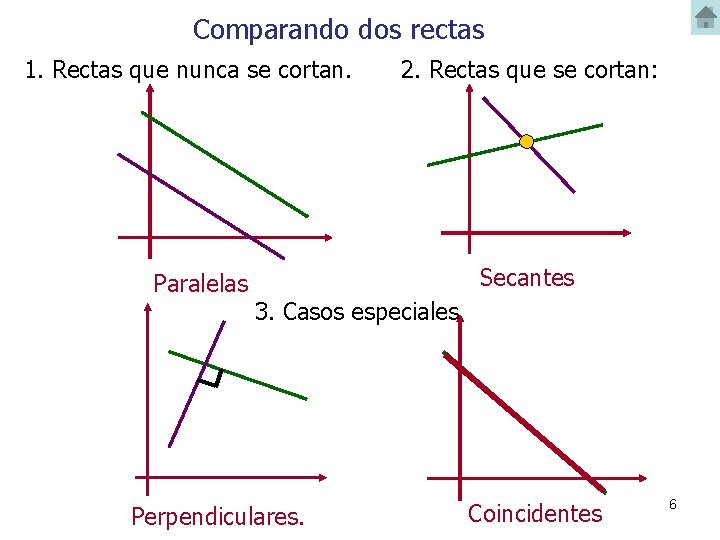
Comparando dos rectas 1. Rectas que nunca se cortan. Paralelas 2. Rectas que se cortan: Secantes 3. Casos especiales Perpendiculares. Coincidentes 6

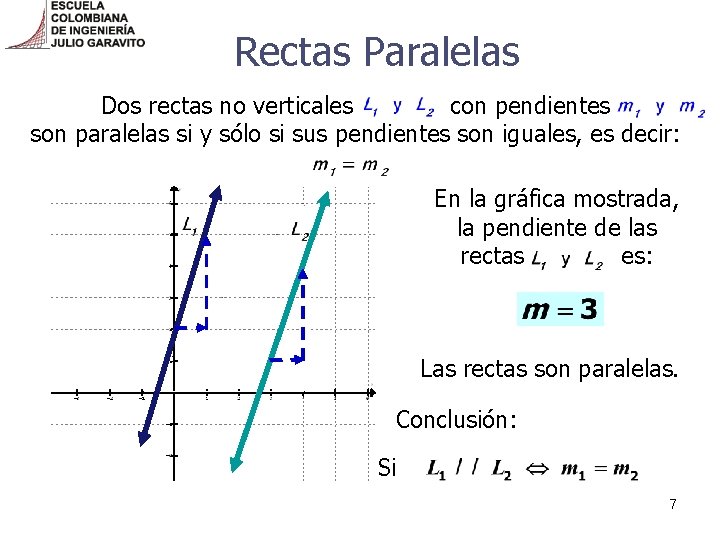
Rectas Paralelas Dos rectas no verticales con pendientes son paralelas si y sólo si sus pendientes son iguales, es decir: En la gráfica mostrada, la pendiente de las rectas es: Las rectas son paralelas. Conclusión: Si 7

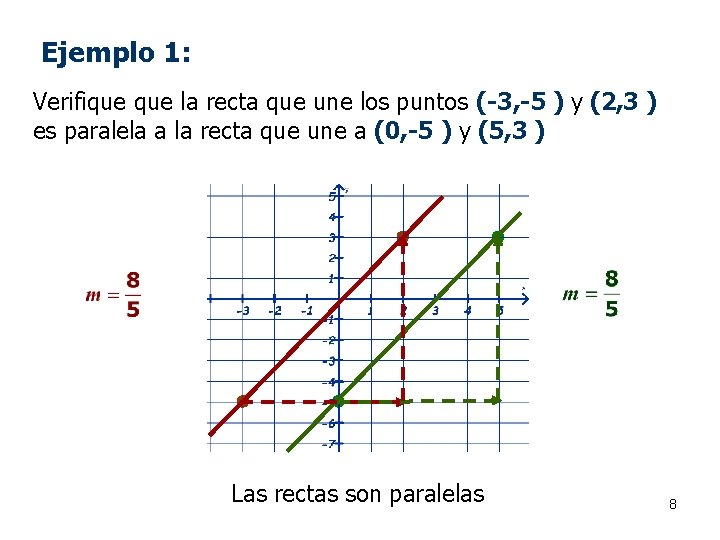
Ejemplo 1: Verifique la recta que une los puntos (-3, -5 ) y (2, 3 ) es paralela a la recta que une a (0, -5 ) y (5, 3 ) Las rectas son paralelas 8

Ejemplo 2: Determinar la ecuación de una recta L que pasa por el punto (-3, 3) y es paralela a la recta: 10 y -8 x=7. Escribimos la ecuación de la recta dada de la forma y=mx+b: Como las rectas son paralelas tienen la misma pendiente. Utilizando la forma pendiente-ordenada al origen: Como (-3, 3) es un punto de la recta, satisface su ecuación. Sustituimos el punto y encontramos b: Por lo tanto la recta pedida es: 9

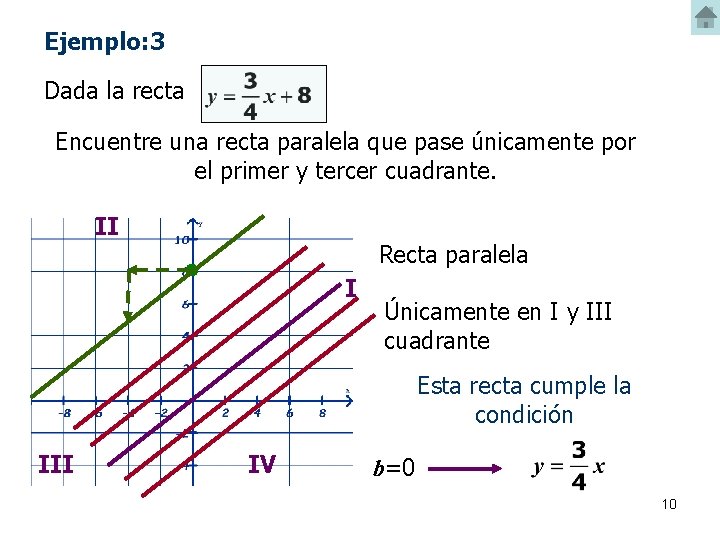
Ejemplo: 3 Dada la recta Encuentre una recta paralela que pase únicamente por el primer y tercer cuadrante. II Recta paralela I Únicamente en I y III cuadrante Esta recta cumple la condición III IV b=0 10

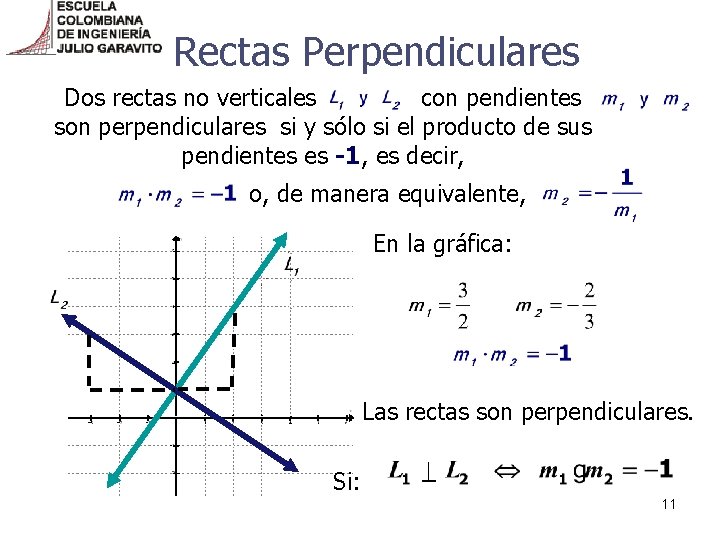
Rectas Perpendiculares Dos rectas no verticales con pendientes son perpendiculares si y sólo si el producto de sus pendientes es -1, es decir, o, de manera equivalente, En la gráfica: Las rectas son perpendiculares. Si: 11

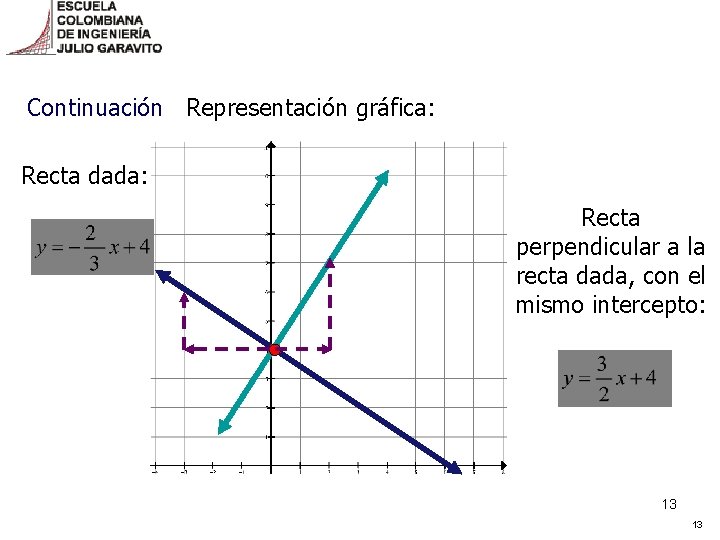
Ejemplo 4: Hallar la ecuación de una recta T que es perpendicular a 2 x+3 y=12 y tiene el mismo punto de corte con el eje y. Escribimos la ecuación de la recta dada de la forma y=mx+b: Las rectas son perpendiculares, el producto de sus pendientes es -1. Para la recta pedida: y 12

Continuación Representación gráfica: Recta dada: Recta perpendicular a la recta dada, con el mismo intercepto: 13 13

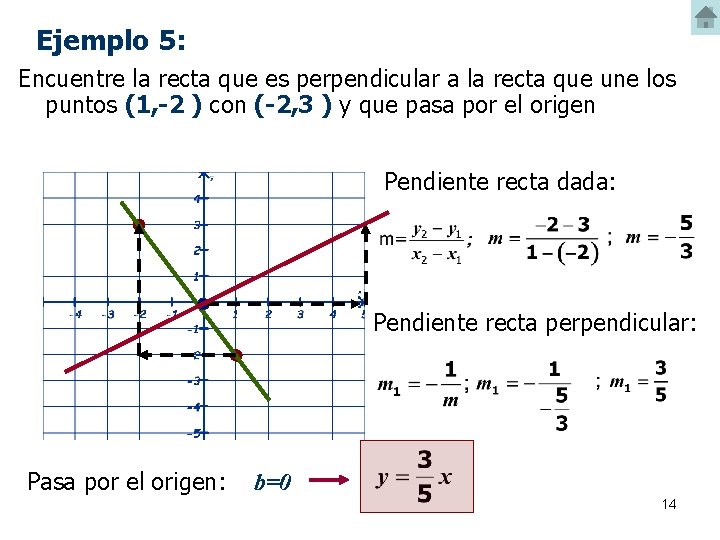
Ejemplo 5: Encuentre la recta que es perpendicular a la recta que une los puntos (1, -2 ) con (-2, 3 ) y que pasa por el origen Pendiente recta dada: Pendiente recta perpendicular: Pasa por el origen: b=0 14

Sistema de ecuaciones lineales Es una reunión de 2 o mas ecuaciones en 2 o mas variables de grado uno. Una solución del sistema consiste en los valores comunes que pueden tomar las variables para hacer verdadera cada una de las ecuaciones que conforman el sistema. Representación: A, B, C, D, E, F 15

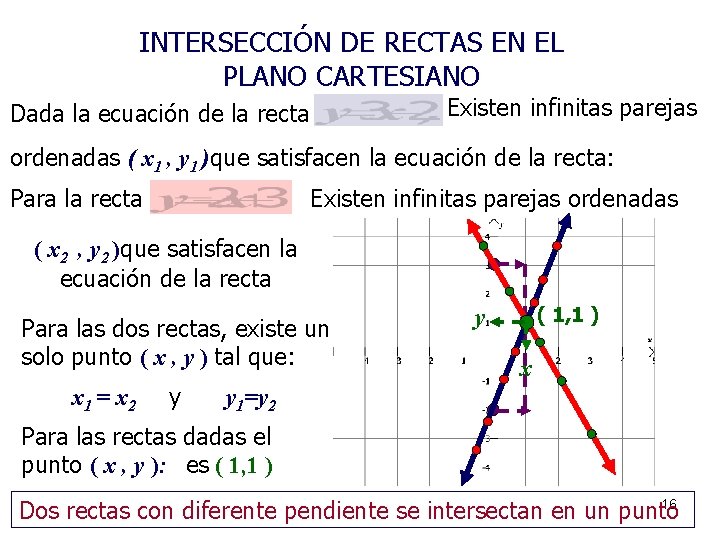
INTERSECCIÓN DE RECTAS EN EL PLANO CARTESIANO Existen infinitas parejas Dada la ecuación de la recta ordenadas ( x 1 , y 1 )que satisfacen la ecuación de la recta: Para la recta Existen infinitas parejas ordenadas ( x 2 , y 2 )que satisfacen la ecuación de la recta Para las dos rectas, existe un solo punto ( x , y ) tal que: x 1 = x 2 y ( 1, 1 ) y x y 1=y 2 Para las rectas dadas el punto ( x , y ): es ( 1, 1 ) 16 Dos rectas con diferente pendiente se intersectan en un punto

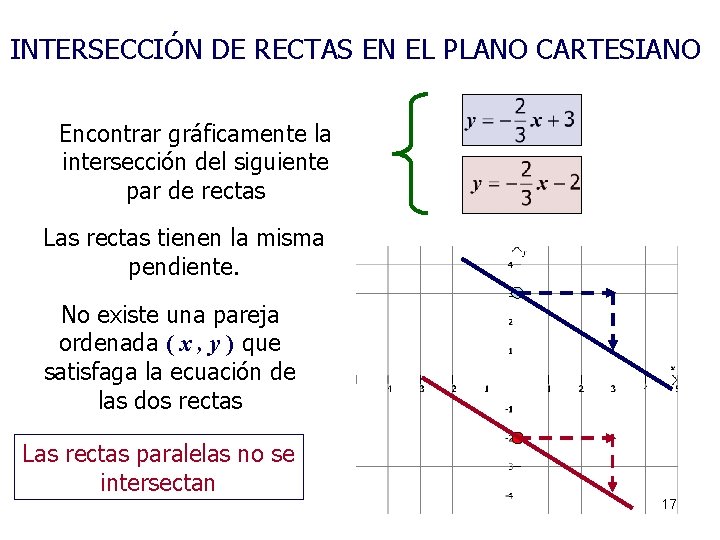
INTERSECCIÓN DE RECTAS EN EL PLANO CARTESIANO Encontrar gráficamente la intersección del siguiente par de rectas Las rectas tienen la misma pendiente. No existe una pareja ordenada ( x , y ) que satisfaga la ecuación de las dos rectas Las rectas paralelas no se intersectan 17

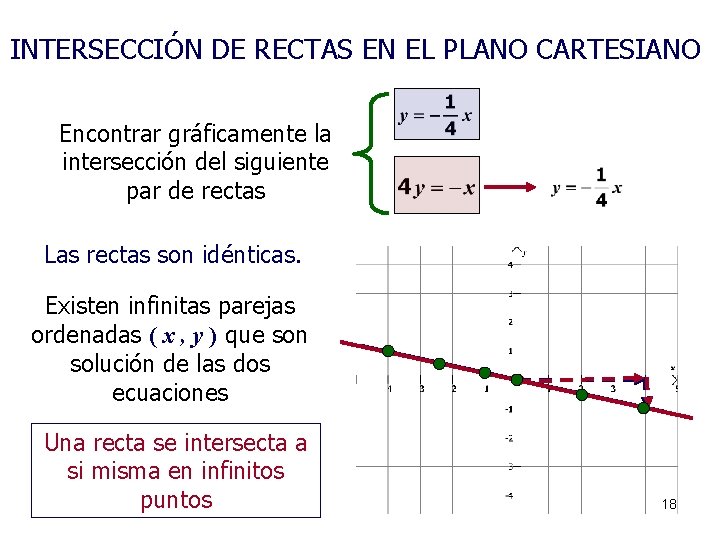
INTERSECCIÓN DE RECTAS EN EL PLANO CARTESIANO Encontrar gráficamente la intersección del siguiente par de rectas Las rectas son idénticas. Existen infinitas parejas ordenadas ( x , y ) que son solución de las dos ecuaciones Una recta se intersecta a si misma en infinitos puntos 18

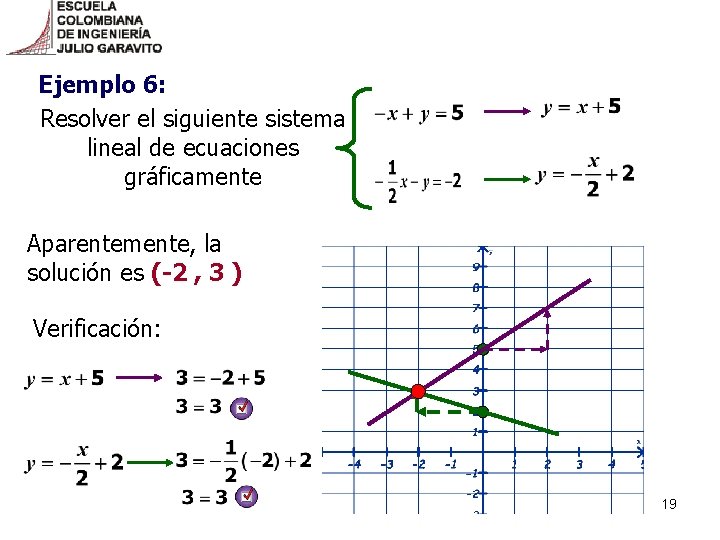
Ejemplo 6: Resolver el siguiente sistema lineal de ecuaciones gráficamente Aparentemente, la solución es (-2 , 3 ) Verificación: 19

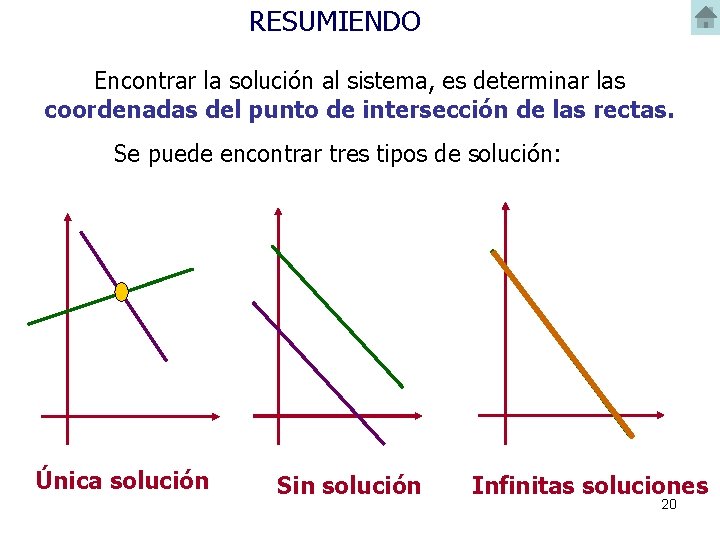
RESUMIENDO Encontrar la solución al sistema, es determinar las coordenadas del punto de intersección de las rectas. Se puede encontrar tres tipos de solución: Única solución Sin solución Infinitas soluciones 20

MÉTODOS ALGEBRAICOS PARA DAR SOLUCIÓN A LOS SISTEMAS DE ECUACIONES LINEALES Para obtener con exactitud la solución de un sistema de ecuaciones se tienen varios métodos ALGEBRÁICOS: SUSTITUCIÓN. IGUALACIÓN ELIMINACIÓN (reducción). 21

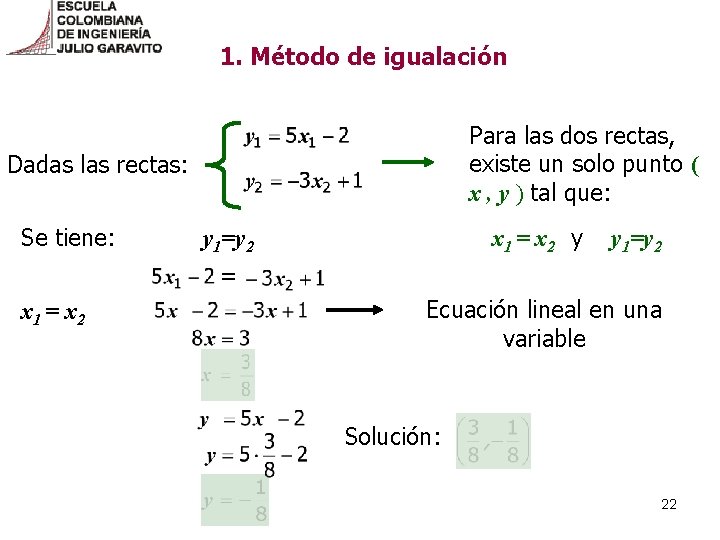
1. Método de igualación Para las dos rectas, existe un solo punto ( x , y ) tal que: Dadas las rectas: Se tiene: x 1 = x 2 y y 1=y 2 = x 1 = x 2 Ecuación lineal en una variable Solución: 22

Ejemplo 7: Resolver el siguiente sistema lineal de ecuaciones Igualando las ecuaciones Sustituyendo: Solución 23

2. Método de sustitución: Dadas las rectas: Se tiene: y 1=y 2 Para las dos rectas, existe un solo punto ( x , y ) tal que: x 1 = x 2 y y 1=y 2 Sustituimos y 2 x 1 = x 2 Ecuación lineal en una variable Solución 24

Ejemplo 8: Resolver el siguiente sistema lineal de ecuaciones Sobre la segunda ecuación Sustituimos y de la primera Identidad Infinitos puntos de intersección Las dos ecuaciones representan una misma recta 25

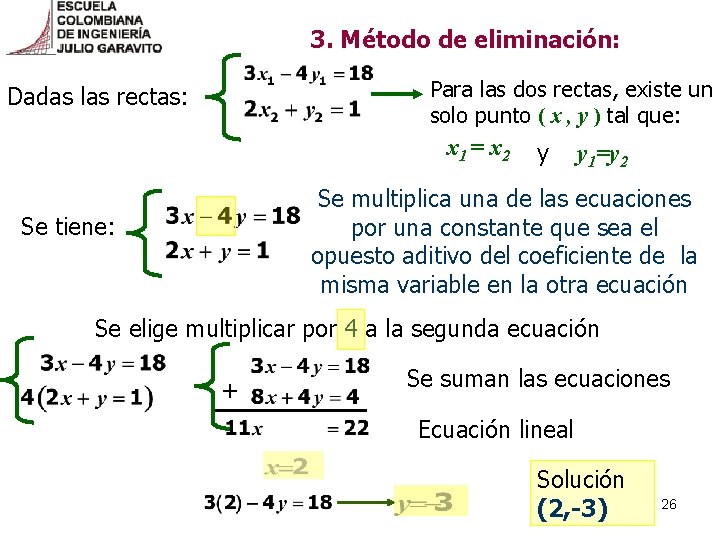
3. Método de eliminación: Para las dos rectas, existe un solo punto ( x , y ) tal que: Dadas las rectas: x 1 = x 2 y y 1=y 2 Se multiplica una de las ecuaciones por una constante que sea el opuesto aditivo del coeficiente de la misma variable en la otra ecuación Se tiene: Se elige multiplicar por 4 a la segunda ecuación + Se suman las ecuaciones Ecuación lineal Solución (2, -3) 26

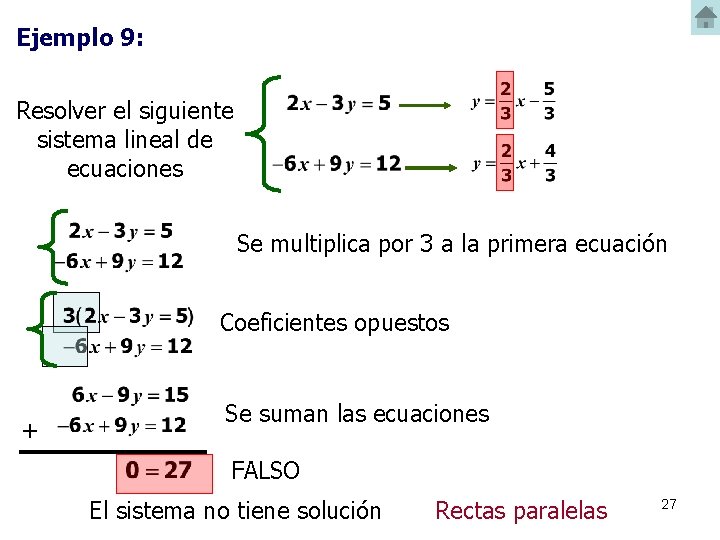
Ejemplo 9: Resolver el siguiente sistema lineal de ecuaciones Se multiplica por 3 a la primera ecuación Coeficientes opuestos + Se suman las ecuaciones FALSO El sistema no tiene solución Rectas paralelas 27

GENERALIDADES DE LOS SISTEMAS DE ECUACIONES Cuando un sistema de ecuaciones : Tiene una única solución se dice que es consistente. Tiene infinitas soluciones es consistente las ecuaciones son dependientes. No tiene solución se dice que es inconsistente. 28

PROBLEMAS DE APLICACIÓN Ejemplo 9: En un corral hay gallinas y borregos. Los animales en total, tienen 60 cabezas y 150 patas. ¿Cuántas gallinas y cuántos borregos hay en el corral? g=cantidad de gallinas b=cantidad de borregos Todos los animales tienen una cabeza Las gallinas tienen dos patas y los borregos tienen cuatro 29

Continuación: Sistema lineal de ecuaciones Sobre la segunda ecuación, sustituimos 15 borregos 45 gallinas 30

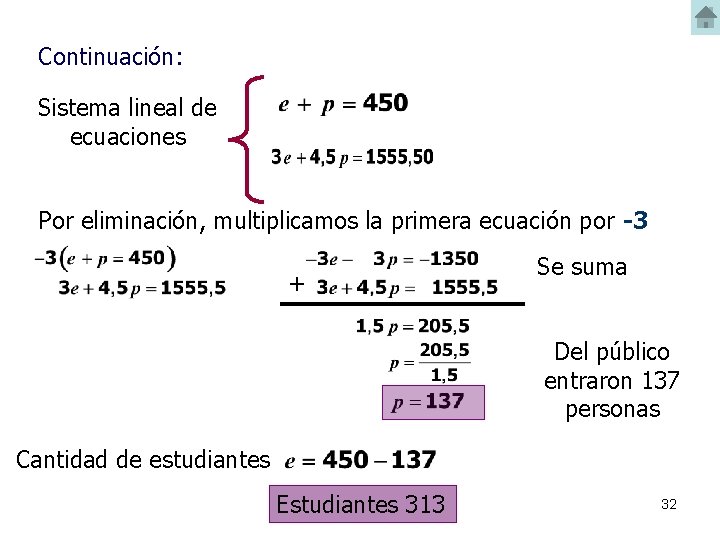
PROBLEMAS DE APLICACIÓN Ejemplo 10: El precio de admisión a una obra de teatro fue de $3, 00 para estudiantes y $4, 50 para el público en general. Si se vendieron 450 boletos para un total de $1. 555, 50. ¿Cuántos estudiantes entraron a la obra? e=cantidad de estudiantes que entraron a la obra p=cantidad de personas del público que entró a la obra Total de asistentes a la obra es igual al número de boletos vendidos: Total de dinero es igual al recaudo por las boletas de estudiante mas el recaudo por las boletas del público 31

Continuación: Sistema lineal de ecuaciones Por eliminación, multiplicamos la primera ecuación por -3 + Se suma Del público entraron 137 personas Cantidad de estudiantes Estudiantes 313 32