VECTORES RECTAS 1 EL PLANO AFN TRES PUNTOS

VECTORES RECTAS 1

EL PLANO AFÍN • TRES PUNTOS ALINEADOS • PUNTO MEDIO DE UN SEGMENTO • SIMÉTRICO DE UN PUNTO RESPECTO DE OTRO 2

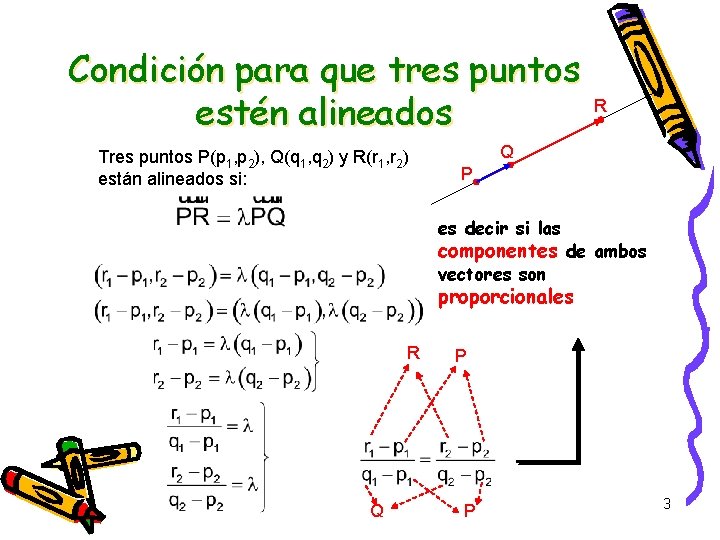
Condición para que tres puntos estén alineados Tres puntos P(p 1, p 2), Q(q 1, q 2) y R(r 1, r 2) están alineados si: R Q P es decir si las componentes de ambos vectores son proporcionales R Q P P 3

Punto medio de un segmento Q M Si M(x, y) es el punto medio de dos P(p 1, p 2) y Q(q 1, q 2): P Por análogo procedimiento podremos hallar las coordenadas de los puntos que dividen un segmento en partes iguales M(x, y) es el punto medio de P(p 1, p 2) y Q(q 1, q 2): 4

Simétrico de un punto respecto de P’ otro Q Para hallar el simétrico P’(x, y) de un punto P(p 1, p 2) respecto de Q(q 1, q 2): P O bien: Q es el punto medio de PP’: 5

Ecuaciones de la recta • • ECUACIÓN VECTORIAL ECUACIONES PARAMÉTRICAS ECUACIÓN CONTÍNUA ECUACIÓN GENERAL , IMPLÍCITA O CARTESIANA • ECUACIÓN EXPLÍCITA • CONDICIÓN DE PARALELISMO ENTRE RECTAS 6

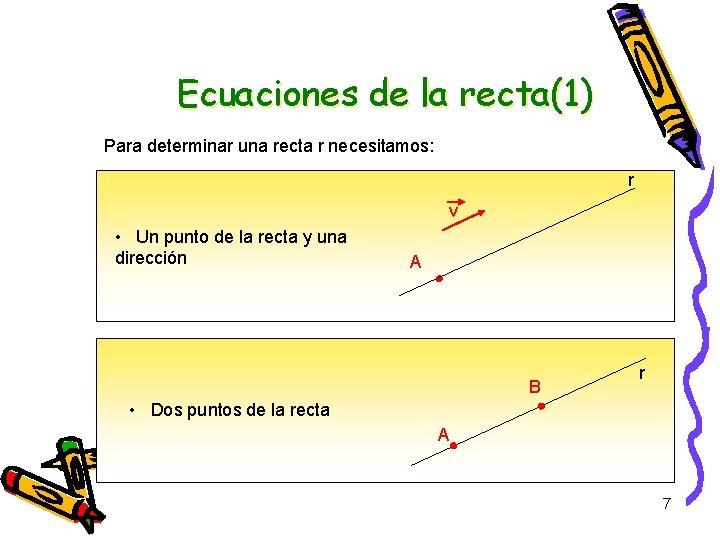
Ecuaciones de la recta(1) Para determinar una recta r necesitamos: r v • Un punto de la recta y una dirección A B r • Dos puntos de la recta A 7

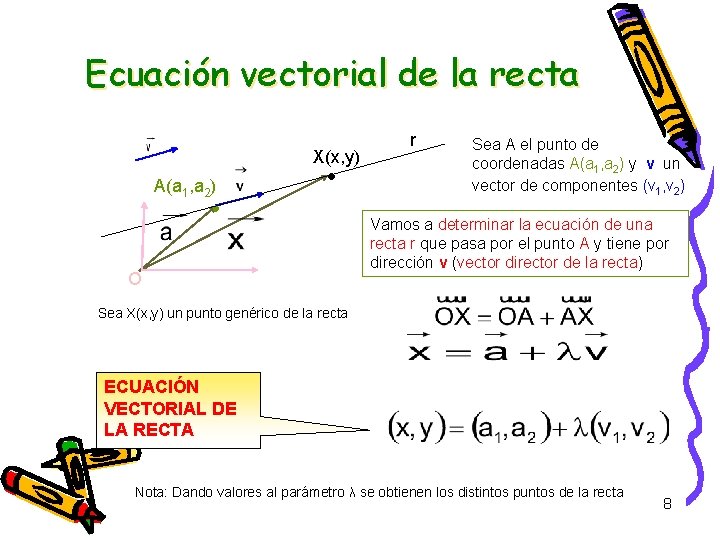
Ecuación vectorial de la recta X(x, y) A(a 1, a 2) O r Sea A el punto de coordenadas A(a 1, a 2) y v un vector de componentes (v 1, v 2) Vamos a determinar la ecuación de una recta r que pasa por el punto A y tiene por dirección v (vector director de la recta) Sea X(x, y) un punto genérico de la recta ECUACIÓN VECTORIAL DE LA RECTA Nota: Dando valores al parámetro λ se obtienen los distintos puntos de la recta 8

Ecuaciones de la recta r que pasa por el punto A(a 1, a 2) y cuyo vector direccional es v=(v 1, v 2) Dada la ecuación vectorial de la recta r: Multiplicando por el escalar: Sumando: Igualando componentes: Despejando el parámetro e igualando: ECUACIONES PARAMÉTRICAS DE LA RECTA ECUACIÓN CONTÍNUA DE LA RECTA Multiplicando y pasando todo al primer miembro de la igualdad: Si llamamos: Tenemos: ECUACIÓN GENERAL DE LA RECTA 9

Ecuaciones de la recta r que pasa por el punto A(2, -3) y cuyo vector direccional es v=(5, -1) Dada la ecuación vectorial de la recta r: Multiplicando por el escalar: Sumando: Igualando componentes: Despejando el parámetro e igualando: ECUACIONES PARAMÉTRICAS DE LA RECTA ECUACIÓN CONTÍNUA DE LA RECTA Multiplicando y pasando todo al primer miembro de la igualdad: Tenemos: ECUACIÓN GENERAL DE LA RECTA 10

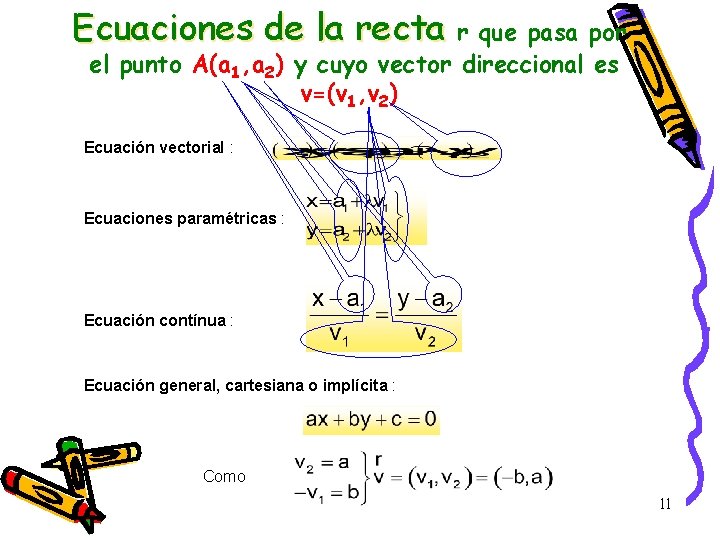
Ecuaciones de la recta r que pasa por el punto A(a 1, a 2) y cuyo vector direccional es v=(v 1, v 2) Ecuación vectorial : Ecuaciones paramétricas : Ecuación contínua : Ecuación general, cartesiana o implícita : Como 11

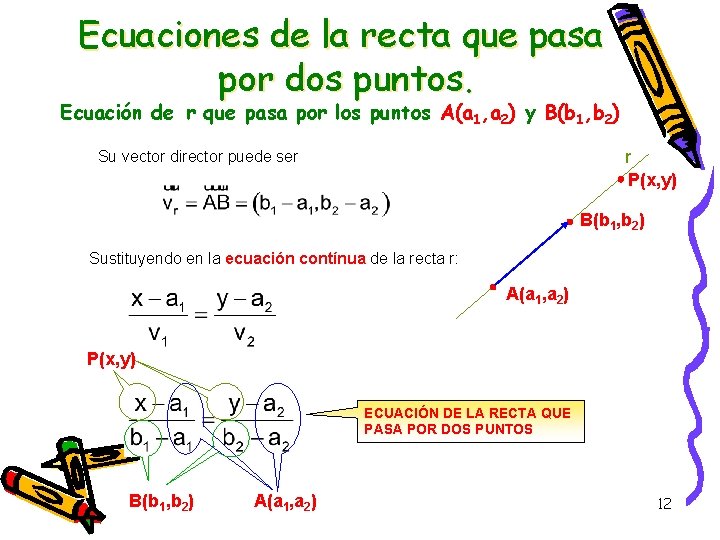
Ecuaciones de la recta que pasa por dos puntos. Ecuación de r que pasa por los puntos A(a 1, a 2) y B(b 1, b 2) Su vector director puede ser r P(x, y) B(b 1, b 2) Sustituyendo en la ecuación contínua de la recta r: A(a 1, a 2) P(x, y) ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS B(b 1, b 2) A(a 1, a 2) 12

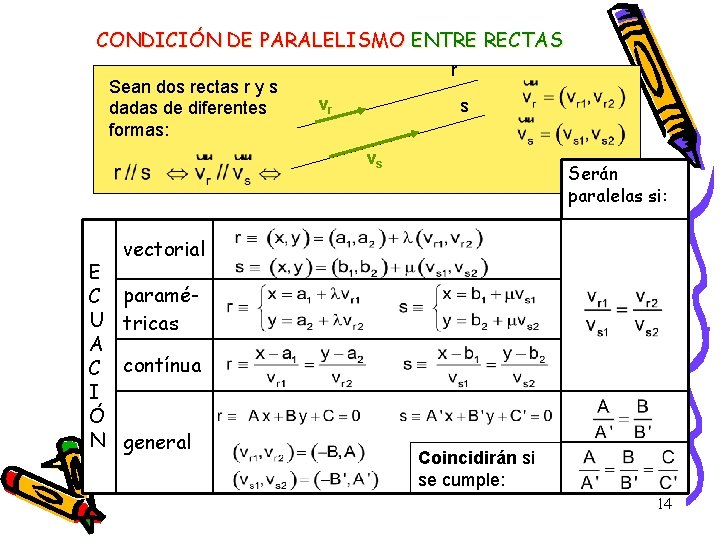
CONDICIÓN DE PARALELISMO ENTRE RECTAS Sean vr y vs los vectores directores de dos rectas r y s paralelas. r vr s vs Si dos rectas r y s son paralelas, también lo son sus vectores directores: (Sus componentes serán proporcionales) 13

CONDICIÓN DE PARALELISMO ENTRE RECTAS Sean dos rectas r y s dadas de diferentes formas: r vr s vs E C U A C I Ó N Serán paralelas si: vectorial paramétricas contínua general Coincidirán si se cumple: 14

PRODUCTO ESCALAR DE DOS VECTORES • • • DEFINICIÓN PROPIEDADES MÓDULO DE UN VECTOR ÁNGULO QUE FORMAN DOS VECTORES ÁNGULO QUE FORMAN DOS RECTAS CONDICIÓN DE PARALELISMO Y PERPENDICULARIDAD ENTRE RECTAS POSICIÓN RELATIVA DE DOS RECTAS PENDIENTE DE UNA RECTA ECUACIÓN PUNTO-PENDIENTE DE LA RECTA DISTANCIA DE UN PUNTO A UNA RECTA. 15

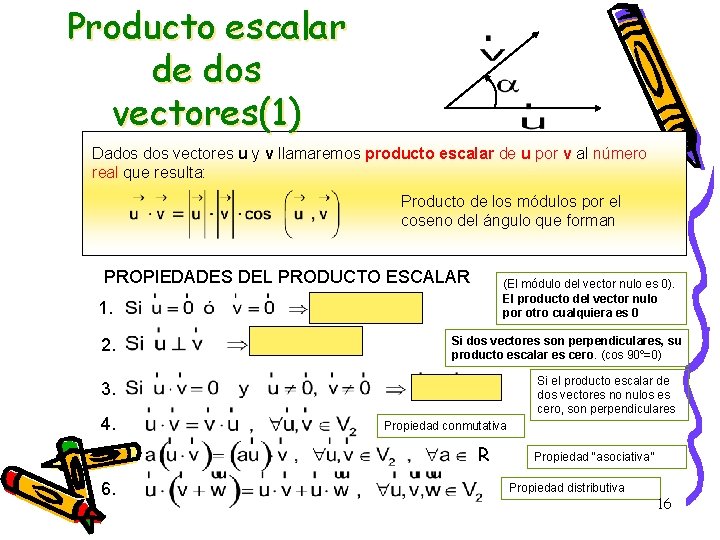
Producto escalar de dos vectores(1) Dados vectores u y v llamaremos producto escalar de u por v al número real que resulta: Producto de los módulos por el coseno del ángulo que forman PROPIEDADES DEL PRODUCTO ESCALAR (El módulo del vector nulo es 0). El producto del vector nulo por otro cualquiera es 0 1. 2. Si dos vectores son perpendiculares, su producto escalar es cero. (cos 90º=0) Si el producto escalar de dos vectores no nulos es cero, son perpendiculares 3. 4. 5. 6. Propiedad conmutativa R Propiedad “asociativa” Propiedad distributiva 16

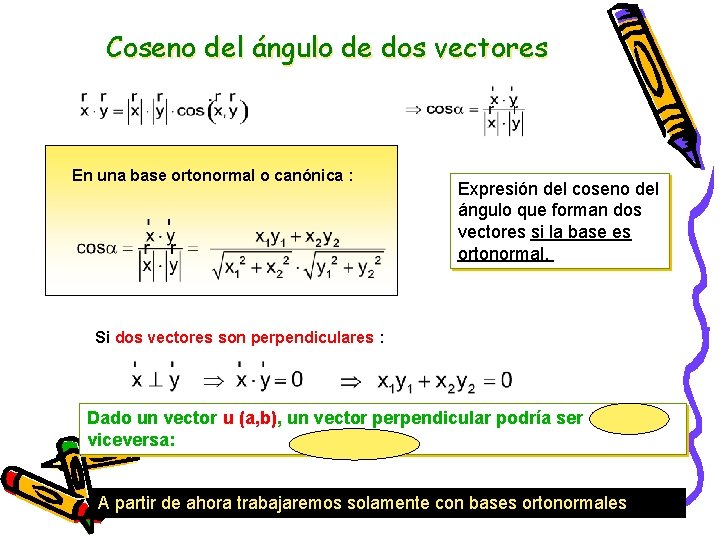
Coseno del ángulo de dos vectores En una base ortonormal o canónica : Expresión del coseno del ángulo que forman dos vectores si la base es ortonormal. Si dos vectores son perpendiculares : Dado un vector u (a, b), un vector perpendicular podría ser v(-b, a) y viceversa: a(-b)+ba=0 A partir de ahora trabajaremos solamente con bases ortonormales 17

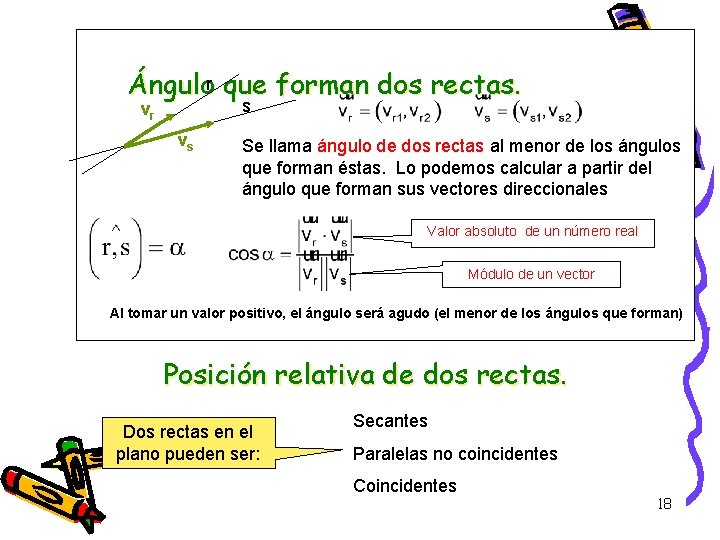
Ángulor que forman dos rectas. s vr vs Se llama ángulo de dos rectas al menor de los ángulos que forman éstas. Lo podemos calcular a partir del ángulo que forman sus vectores direccionales Valor absoluto de un número real Módulo de un vector Al tomar un valor positivo, el ángulo será agudo (el menor de los ángulos que forman) Posición relativa de dos rectas. Dos rectas en el plano pueden ser: Secantes Paralelas no coincidentes Coincidentes 18

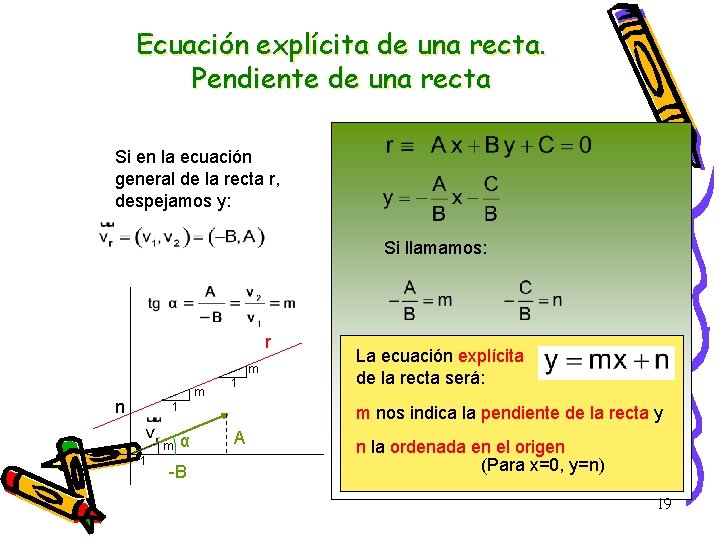
Ecuación explícita de una recta. Pendiente de una recta Si en la ecuación general de la recta r, despejamos y: Si llamamos: r m m n 1 1 m 1 La ecuación explícita de la recta será: m nos indica la pendiente de la recta y α -B A n la ordenada en el origen (Para x=0, y=n) 19

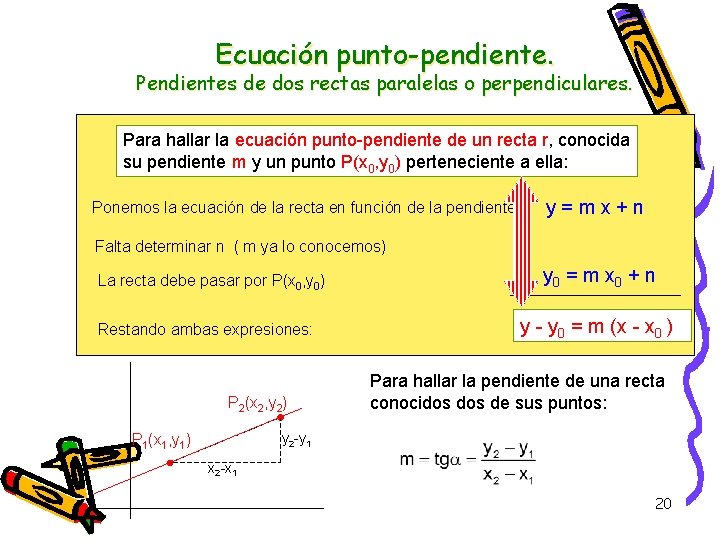
Ecuación punto-pendiente. Pendientes de dos rectas paralelas o perpendiculares. Para hallar la ecuación punto-pendiente de un recta r, conocida su pendiente m y un punto P(x 0, y 0) perteneciente a ella: Ponemos la ecuación de la recta en función de la pendiente: y=mx+n Falta determinar n ( m ya lo conocemos) La recta debe pasar por P(x 0, y 0) Restando ambas expresiones: P 2(x 2, y 2) y 0 = m x 0 + n y - y 0 = m (x - x 0 ) Para hallar la pendiente de una recta conocidos de sus puntos: y 2 -y 1 P 1(x 1, y 1) x 2 -x 1 20

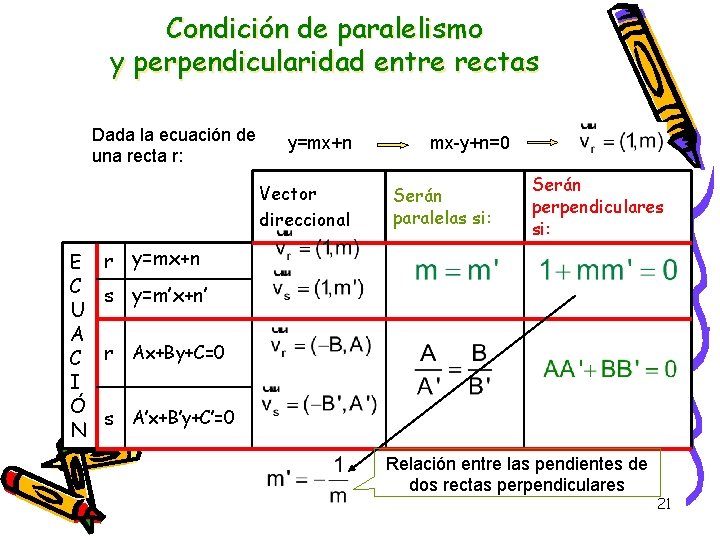
Condición de paralelismo y perpendicularidad entre rectas Dada la ecuación de una recta r: y=mx+n Vector direccional E C U A C I Ó N mx-y+n=0 Serán paralelas si: Serán perpendiculares si: r y=mx+n s y=m’x+n’ r Ax+By+C=0 s A’x+B’y+C’=0 Relación entre las pendientes de dos rectas perpendiculares 21

DISTANCIA ENTRE DOS PUNTOS 22

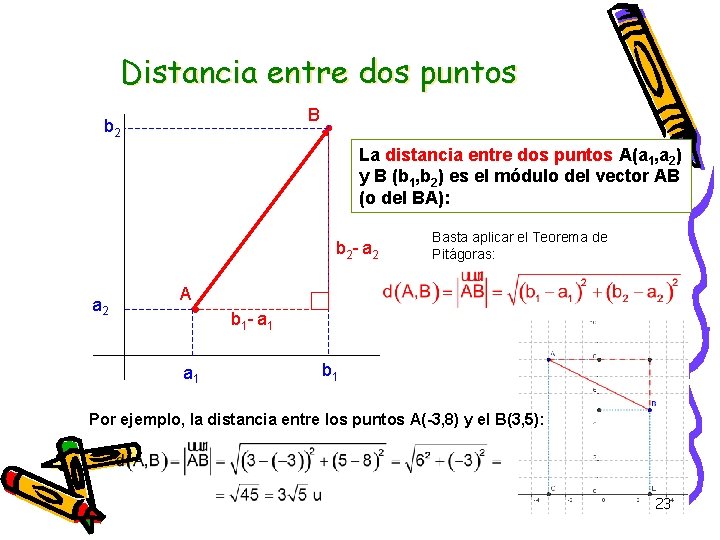
Distancia entre dos puntos B b 2 La distancia entre dos puntos A(a 1, a 2) y B (b 1, b 2) es el módulo del vector AB (o del BA): b 2 - a 2 Basta aplicar el Teorema de Pitágoras: A b 1 - a 1 b 1 Por ejemplo, la distancia entre los puntos A(-3, 8) y el B(3, 5): 23

Hoja de problemas con soluciones: http: //www. educa. aragob. es/iesitaza/DAPARTAM/matemat/06 ge ometriaplano. pdf Teoría y ejercicios: http: //personales. unican. es/gonzaleof/# Maneja vectores: http: //www. xtec. es/~jbartrol/vectores/index. html http: //platea. pntic. mec. es/anunezca/Unid. Did. Vectores/Index/index. htm 24