MTRICA DEL ESPACIO U D 11 Angel Prieto

MÉTRICA DEL ESPACIO U. D. 11 * @ Angel Prieto Benito 2º BCT Matemáticas 2º Bachillerato C. T. 1

MEDIATRIZ DE UN SEGMENTO U. D. 11. 2 * @ Angel Prieto Benito 2º BCT Matemáticas 2º Bachillerato C. T. 2

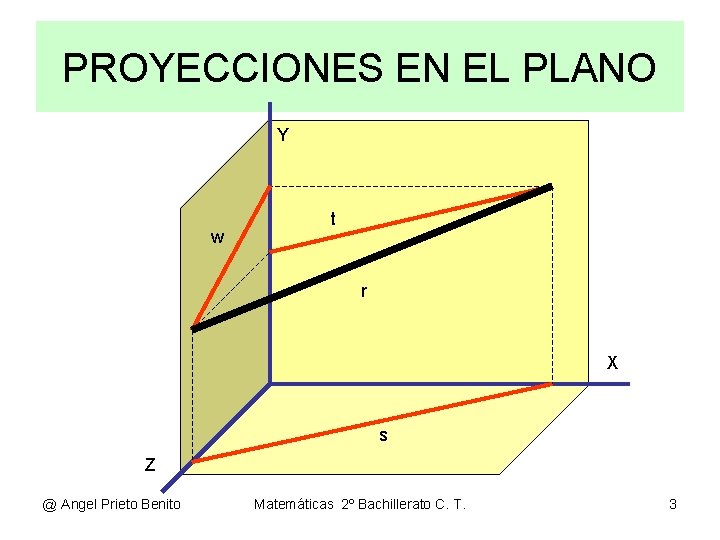
PROYECCIONES EN EL PLANO Y w t r X s Z @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 3

PROYECCIONES EN EL PLANO • PROYECCIONES ORTOGONALES DE UNA RECTA EN PLANOS • • • Sea la recta r: {Ax+By+Cz+D=0, A’x+B’y+C’z+D’=0} cualquiera. También r: (a, b, c) + λ(u 1, u 2, u 3). Proyectar una recta de forma ortogonal es, como se ha visto en el dibujo anterior, obtener sus proyecciones sobre los planos del sistema de coordenadas cartesiano. Cada proyección de la recta en el espacio será una recta definida en un plano. Sobre el plano XY: Faltará su coordenada en z. c + λ. u 3 = 0 λ = - c / u 3 Quedará r: x = a + (- c / u 3). u 1 ; y = b + (- c / u 3). u 2 • • • Sobre el plano XZ: Faltará su coordenada en y. b + λ. u 2 = 0 λ = - b / u 2 Quedará r: x = a + (- b / u 2). u 1 ; z = c + (- b / u 2). u 3 Sobre el plano YZ: Faltará su coordenada en x. a + λ. u 1 = 0 λ = - a / u 1 Quedará r: y = b + (- a / u 1). u 2 ; z = c + (- a / u 1). u 3 @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 4

Ejemplo • EJEMPLO • • • Sea la recta r: (x, y, z) = (4, 2, 6) + λ (1, 1, 1). Sobre el plano XY: Faltará su coordenada en z. (x, y, z) = (4, 2, 6) + λ (1, 1, 1). 6 + λ. 1 = 0 λ = - 6 / 1 = - 6 Quedará r: x = 4 + (- 6). 1 = - 2 ; y = 2 + (- 6). 1 = - 4 • • • Sobre el plano XZ: Faltará su coordenada en y. (x, y, z) = (4, 2, 6) + λ (1, 1, 1). 2 + λ. 1 = 0 λ = - 2 / 1 = - 2 Quedará r: x = 4 + (- 2). 1 = 2 ; z = 6 + (- 2). 1 = 4 Sobre el plano YZ: Faltará su coordenada en x. (x, y, z) = (4, 2, 6) + λ (1, 1, 1). 4 + λ. 1 = 0 λ = - 4 / 1 = - 4 Quedará r: y = 2 + (- 4). 1 = - 2 ; z = 6 + (- 4). 1 = 2 @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 5

MEDIATRIZ DE SEGMENTO • • • • PUNTO MEDIO DE UN SEGMENTO Punto medio de un segmento, de extremos A(x 1, y 1, z 1) y B(x 2, y 2, z 2) es aquel que se encuentra a igual distancia de los extremos. Pm = [(x 1 + x 2, )/2 , (y 1 + y 2)/2 , (z 1 + z 2)/2 ] CÁLCULO DE LA MEDIATRIZ Mediatriz de un segmento AB es la recta que, pasando por el punto medio del segmento, es perpendicular al mismo. Sea P un punto genérico , y A y B los B extremos del segmento. d (P, A) = d (P, B) d √ [ (x – x 1) 2 + (y – y 1) 2 + (z – z 1) 2 ] = = √ [ (x – x 2) 2 + (y – y 2) 2 + (z – z 1) 2 ] r A P Se eleva todo al cuadrado, se reducen d términos semejantes y el resultado es la recta r, la mediatriz. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 6

Ejemplos • Ejemplo 1 • Hallar la ecuación de la mediatriz del segmento de extremos A(2, -1, 1) y B(3, 5, -2) • • • d (P, A) = d (P, b) √ [ (x – 2) 2 + (y + 1) 2 + (z – 1) 2 ] = √ [ (x – 3) 2 + (y – 5) 2 + (z + 2) 2 ] Se eleva todo al cuadrado: (x – 2) 2 + (y + 1) 2 + (z – 1) 2 = (x – 3) 2 + (y – 5) 2 + (z + 2) 2 x 2 – 4 x + 4 + y 2 + 2 y + 1 + z 2 – 2 z + 1 = = x 2 – 6 x + 9 + y 2 – 10 y + 25 + z 2 + 4 z + 4 Se reducen términos semejantes: – 4 x + 4 + 2 y + 1 – 2 z + 1 = – 6 x + 9 – 10 y + 25 + 4 z + 4 2 x + 12 y – 6 z – 32 = 0 x + 6. y – 3. z – 16 = 0 La mediatriz del segmento AB es un plano, o sea cualquier recta contenida en dicho plano y que pase por el centro del segmento: M=(2, 5 , 2 , -0, 5) • @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 7

Ejemplos • Ejemplo 2 • Hallar la ecuación de la mediatriz del segmento de extremos A(2, 0, 2) y B(0, - 4, 0) • • d (P, A) = d (P, b) √ [ (x – 2)2 + y 2 + (z – 2)2] = √ [ x 2 + (y + 4)2 + z 2 ] Se eleva todo al cuadrado: (x – 2)2 + y 2 + (z – 2)2 = x 2 + (y + 4)2 + z 2 x 2 – 4 x + 4 + y 2 + z 2 – 4 z + 4 = x 2 + y 2 + 6 y + 9 + z 2 Se reducen términos semejantes: – 4 x + 4 – 4 z + 4 = 6 y + 9 4 x + 6 y + 4 z + 1 = 0 • • Solución: Un plano. Todas las rectas que pasando por el punto M(1, -2, 1) forman parte del plano dado. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 8

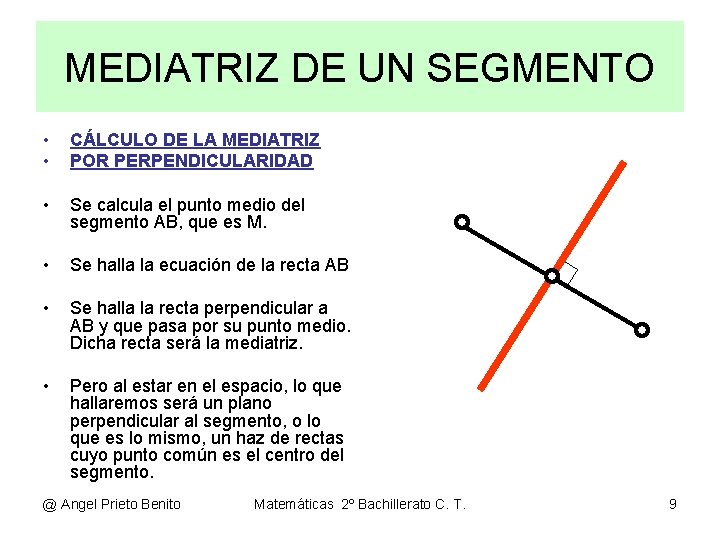
MEDIATRIZ DE UN SEGMENTO • • CÁLCULO DE LA MEDIATRIZ POR PERPENDICULARIDAD • Se calcula el punto medio del segmento AB, que es M. • Se halla la ecuación de la recta AB • Se halla la recta perpendicular a AB y que pasa por su punto medio. Dicha recta será la mediatriz. • Pero al estar en el espacio, lo que hallaremos será un plano perpendicular al segmento, o lo que es lo mismo, un haz de rectas cuyo punto común es el centro del segmento. @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 9

• Ejemplo 3 • Hallar la ecuación de la mediatriz del segmento de extremos A(2, -1, 0) y B(4, 1, 2) • SOLUCIÓN • • Se calcula el punto medio M: M=((2+4)/2 , (-1+1)/2 , (0+2)/2) = (3 , 0 , 1) • • Ecuación de la recta AB: AB=(A, v) ; AB=((2, -1, 0), (4 -2, 1+1, 2 -0)) v(2 , 2) • • Perpendicular a AB por M: Un vector u perpendicular a v es tal que u. v = 0 (producto escalar) Sea u(a, b, c) u. v = (a, b, c). (2, 2, 2) = 2 a + 2 b + 2 c = 0 Un vector u válido cualquiera es u(1, 1, – 2) Por último la recta mediatriz es: m=(M, u) m: (x, y, z) = (3, 0, 1) + λ. (1, 1, – 2) @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 10

• Ejemplo 4 • Hallar la ecuación de la mediatriz del segmento de extremos A(0, 1, a) y B(2, 3, -a) • SOLUCIÓN • • Se calcula el punto medio M: M=((0+2)/2 , (1+3)/2 , (a-a)/2) = (1 , 2 , 0) • • Ecuación de la recta AB: AB=(A, v) ; AB=((0, 1, a), (2 -0, 3 -1, -a-a)) v(2 , – 2 a) • • Perpendicular a AB por M: Un vector u perpendicular a v es tal que u. v = 0 (producto escalar) Sea u(m, n, p) u. v = (m, n, p). (2, 2, -2 a) = 2 m + 2 n – 2 ap = 0 Un vector u válido cualquiera es u(1, – 1, 0) Por último la recta mediatriz es: m=(M, u) m: (x, y, z) = (1, 2, 0) + λ. (1, – 1, 0) , que vemos pertenece al plano XY @ Angel Prieto Benito Matemáticas 2º Bachillerato C. T. 11