Vectores y sistemas de vectores Versin Junio de







































- Slides: 68

Vectores y sistemas de vectores Versión: Junio de 2019


FÍSICA GENERAL I Tema 1: Magnitudes físicas. Unidades y medidas Tema 2: Vectores y sistemas de vectores Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 5: Cinemática del sólido rígido Tema 6: Cinemática relativa del punto Tema 7: Dinámica del punto Tema 8: Trabajo y energía I Tema 9: Trabajo y energía II Tema 10: Movimiento del punto bajo fuerzas centrales Tema 11: Dinámica del los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II Tema 2: Vectores y sistemas de vectores Sistemas de referencia y orientación en el espacio: coordenadas cartesianas, polares, cilíndricas y esféricas Magnitudes escalares y vectoriales. Operaciones vectoriales Vectores deslizantes Sistemas de vectores deslizantes. Invariantes. Eje central

Familia de curvas coordenadas y SISTEMA DE COORDENADAS CARTESIANAS ORTOGONALES Familia de curvas coordenadas x

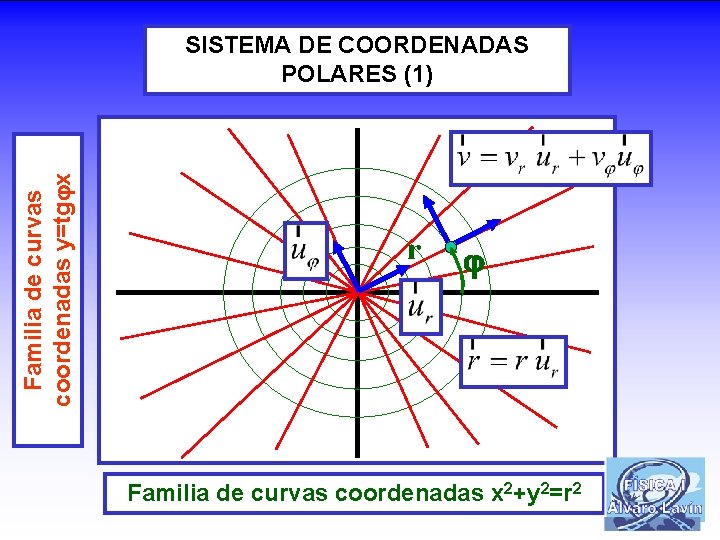
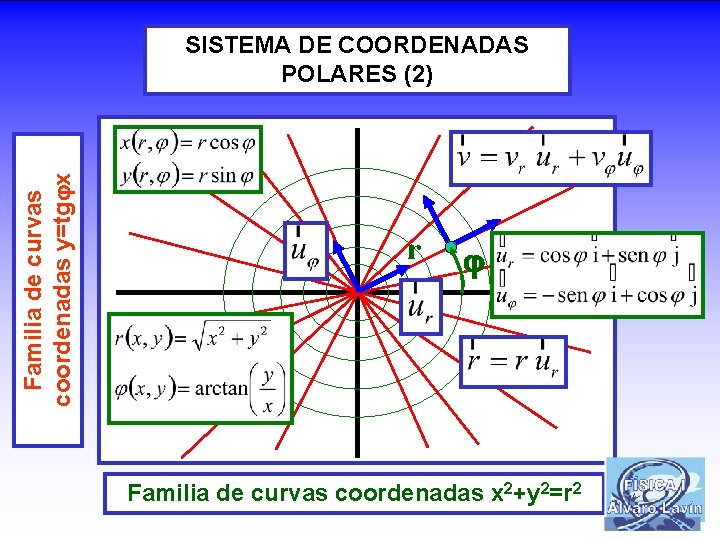
Familia de curvas coordenadas y=tg x SISTEMA DE COORDENADAS POLARES (1) r Familia de curvas coordenadas x 2+y 2=r 2

Familia de curvas coordenadas y=tg x SISTEMA DE COORDENADAS POLARES (2) r Familia de curvas coordenadas x 2+y 2=r 2

y x

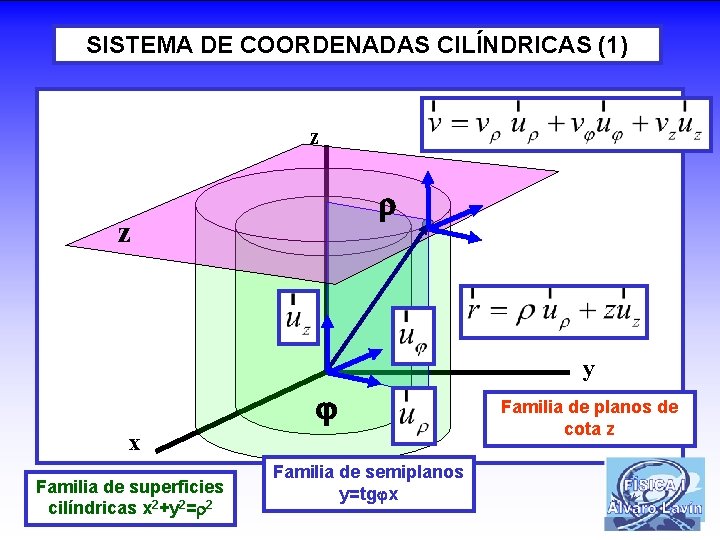
SISTEMA DE COORDENADAS CILÍNDRICAS (1) z z y x Familia de superficies cilíndricas x 2+y 2= 2 Familia de semiplanos y=tg x Familia de planos de cota z

SISTEMA DE COORDENADAS CILÍNDRICAS (2) z z y x

y • Sus coordenadas cilíndricas 150 30 x ¡Hay que tener en cuenta el cuadrante en el que está el punto! • Los vectores unitarios de la referencia natural normalizada en ese punto y 30 150 x

y • Sus coordenadas cilíndricas 210 x 30 ¡Hay que tener en cuenta el cuadrante en el que está el punto! • Los vectores unitarios de la referencia natural normalizada en ese punto y 210 30 x

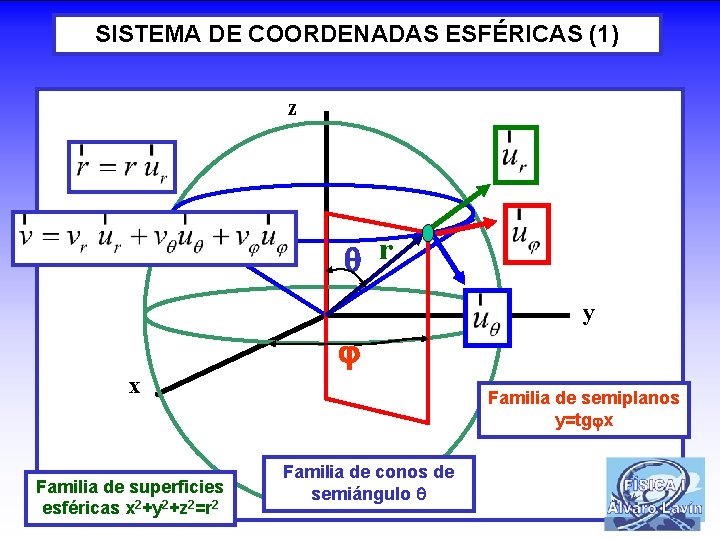
SISTEMA DE COORDENADAS ESFÉRICAS (1) z r y x Familia de superficies esféricas x 2+y 2+z 2=r 2 Familia de semiplanos y=tg x Familia de conos de semiángulo

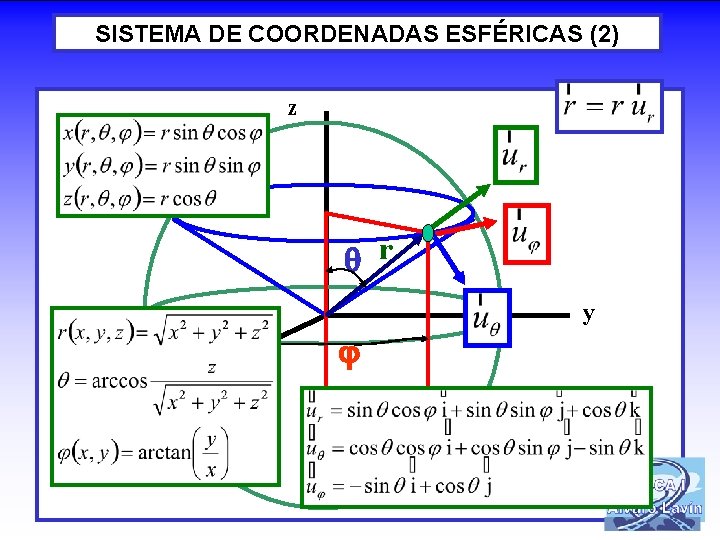
SISTEMA DE COORDENADAS ESFÉRICAS (2) z r y x

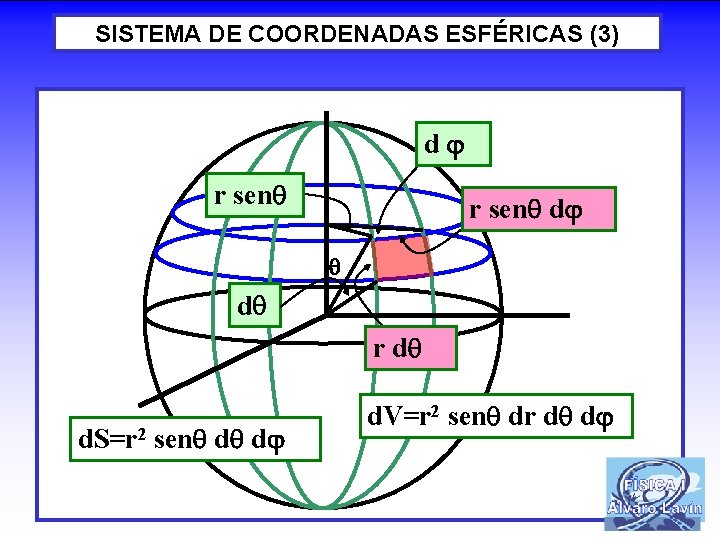
SISTEMA DE COORDENADAS ESFÉRICAS (3) d r sen d d r d d. S=r 2 sen d d d. V=r 2 sen dr d d

Un punto tiene coordenadas cilíndricas (2, /3, 2). Encontrar sus coordenadas esféricas. Ejerc. 2 Exam. Sept. 2008

Un punto tiene coordenadas (3, 2, 1). Encontrar sus coordenadas esféricas.

1 5 9 3 2 6 4 7 10 8 11 12

FÍSICA GENERAL I Tema 1: Magnitudes físicas. Unidades y medidas Tema 2: Vectores y sistemas de vectores Tema 3: Estática de sistemas Tema 4: Cinemática del punto Tema 2: Vectores y sistemas de vectores Sistemas de referencia y orientación en el espacio: coordenadas cartesianas, cilíndricas y esféricas Tema 5: Cinemática del sólido rígido Magnitudes escalares y vectoriales. Operaciones vectoriales Tema 6: Cinemática relativa del punto Vectores deslizantes Tema 7: Dinámica del punto Sistemas de vectores deslizantes. Invariantes. Eje central Tema 8: Trabajo y energía I Tema 9: Trabajo y energía II Tema 10: Movimiento del punto bajo fuerzas centrales Tema 11: Dinámica del los sistemas I Tema 12: Dinámica de los sistemas II Tema 13: Medios deformables I Tema 14: Medios deformables II

Operaciones con vectores (Producto escalar) (1) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 4

Operaciones con vectores (Producto escalar) (2) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 4

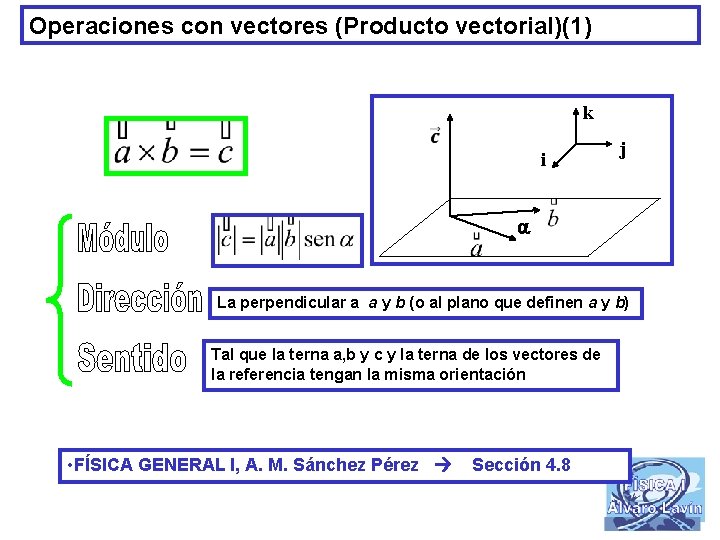
Operaciones con vectores (Producto vectorial)(1) k i j La perpendicular a a y b (o al plano que definen a y b) Tal que la terna a, b y c y la terna de los vectores de la referencia tengan la misma orientación • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 8

Operaciones con vectores (Producto vectorial)(2) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 8

Operaciones con vectores (Producto mixto) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 9. 1 Operaciones con vectores (Doble producto vectorial ) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 9. 2




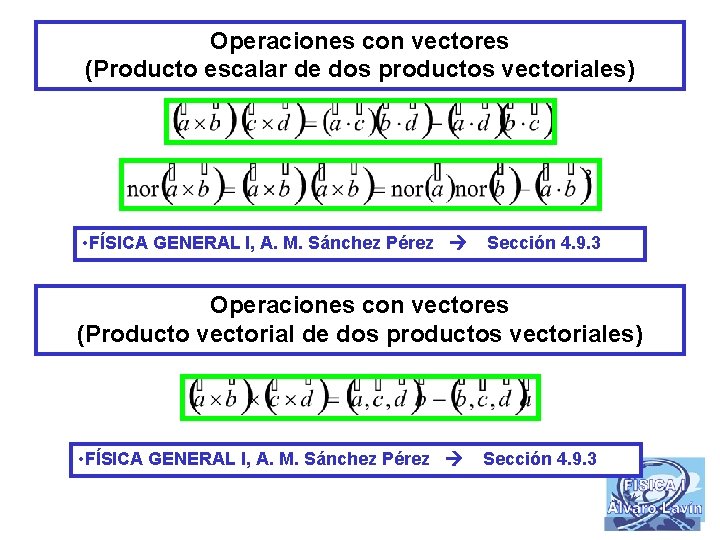
Operaciones con vectores (Producto escalar de dos productos vectoriales) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 9. 3 Operaciones con vectores (Producto vectorial de dos productos vectoriales) • FÍSICA GENERAL I, A. M. Sánchez Pérez Sección 4. 9. 3

El módulo del producto vectorial coincide con el área del paralelogramo que determinan los dos vectores.


MOMENTO CENTRAL DE UN VECTOR O’ O A • El momento central no cambia cuando el vector desliza en su recta soporte • El momento central es nulo cuando la recta soporte del vector pasa por el punto O.

MOMENTO ÁXICO DE UN VECTOR O A • El punto O puede ser cualquier punto del eje • El momento áxico es nulo si la recta soporte del vector intersecta al eje o es paralela al mismo.


1 2 3

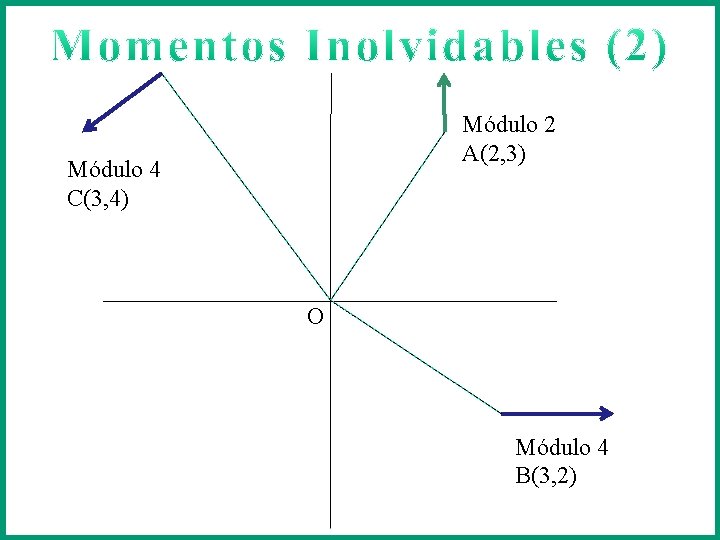
Módulo 2 A(2, 3) Módulo 4 C(3, 4) O Módulo 4 B(3, 2)


SISTEMA DE VECTORES DESLIZANTES SISTEMAS DE VECTORES

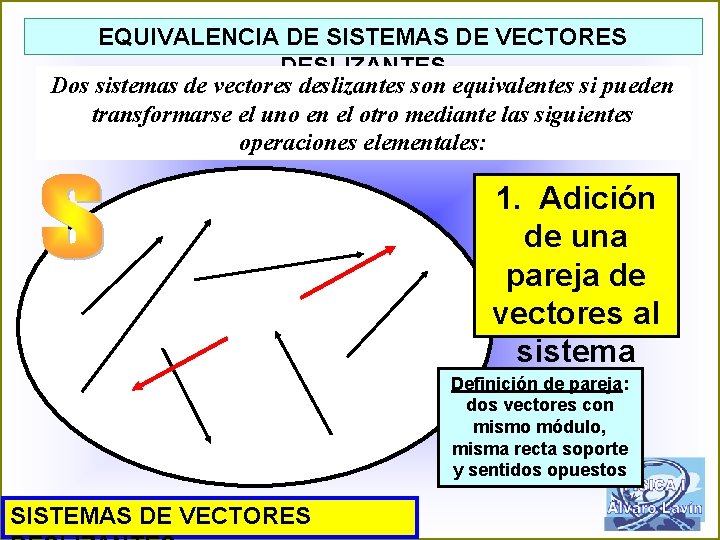
EQUIVALENCIA DE SISTEMAS DE VECTORES DESLIZANTES Dos sistemas de vectores deslizantes son equivalentes si pueden transformarse el uno en el otro mediante las siguientes operaciones elementales: 1. Adición de una pareja de vectores al sistema Definición de pareja: dos vectores con mismo módulo, misma recta soporte y sentidos opuestos SISTEMAS DE VECTORES

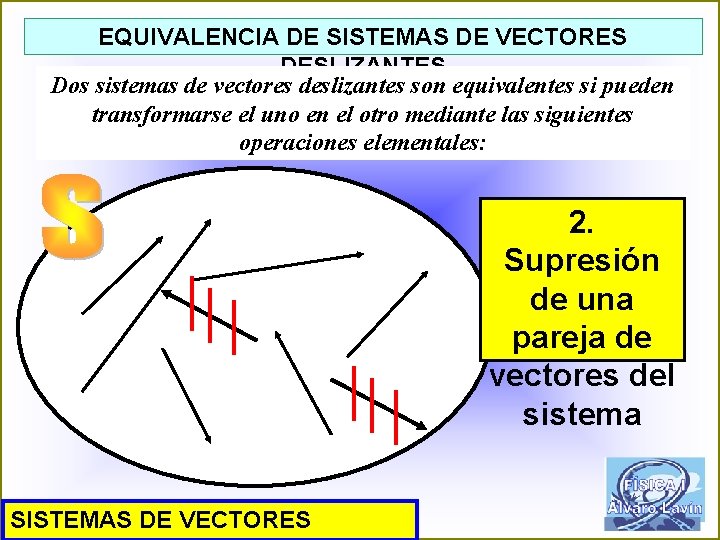
EQUIVALENCIA DE SISTEMAS DE VECTORES DESLIZANTES Dos sistemas de vectores deslizantes son equivalentes si pueden transformarse el uno en el otro mediante las siguientes operaciones elementales: 2. Supresión de una pareja de vectores del sistema SISTEMAS DE VECTORES

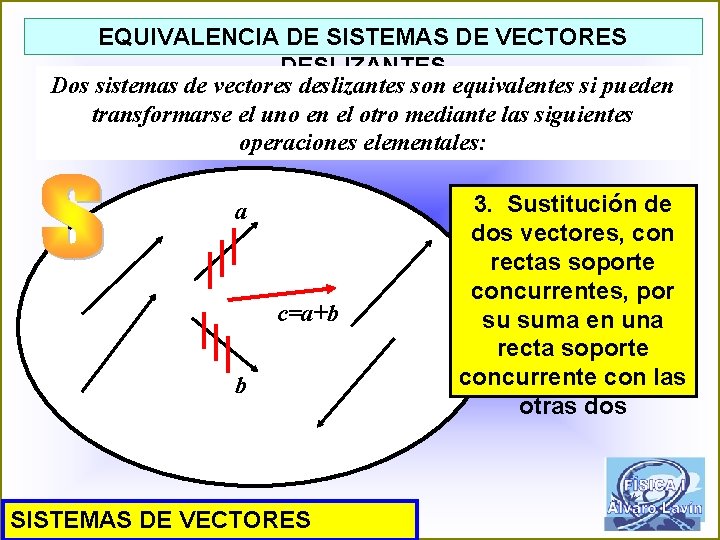
EQUIVALENCIA DE SISTEMAS DE VECTORES DESLIZANTES Dos sistemas de vectores deslizantes son equivalentes si pueden transformarse el uno en el otro mediante las siguientes operaciones elementales: a c=a+b b SISTEMAS DE VECTORES 3. Sustitución de dos vectores, con rectas soporte concurrentes, por su suma en una recta soporte concurrente con las otras dos

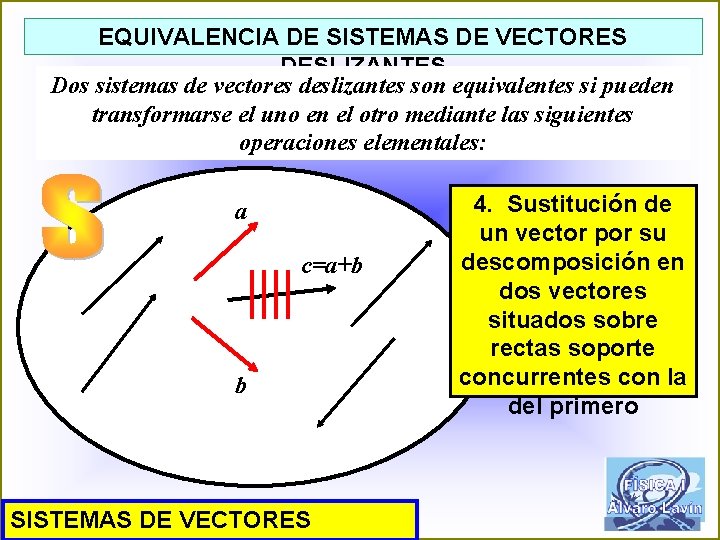
EQUIVALENCIA DE SISTEMAS DE VECTORES DESLIZANTES Dos sistemas de vectores deslizantes son equivalentes si pueden transformarse el uno en el otro mediante las siguientes operaciones elementales: a c=a+b b SISTEMAS DE VECTORES 4. Sustitución de un vector por su descomposición en dos vectores situados sobre rectas soporte concurrentes con la del primero

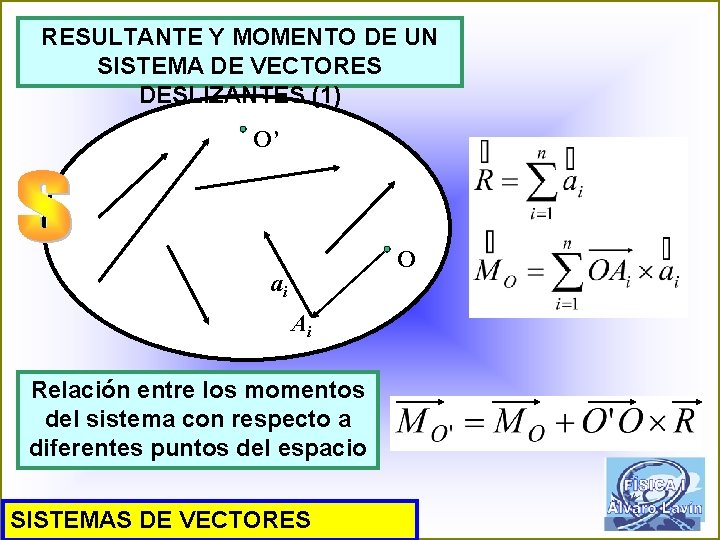
RESULTANTE Y MOMENTO DE UN SISTEMA DE VECTORES DESLIZANTES (1) O’ O ai Ai Relación entre los momentos del sistema con respecto a diferentes puntos del espacio SISTEMAS DE VECTORES

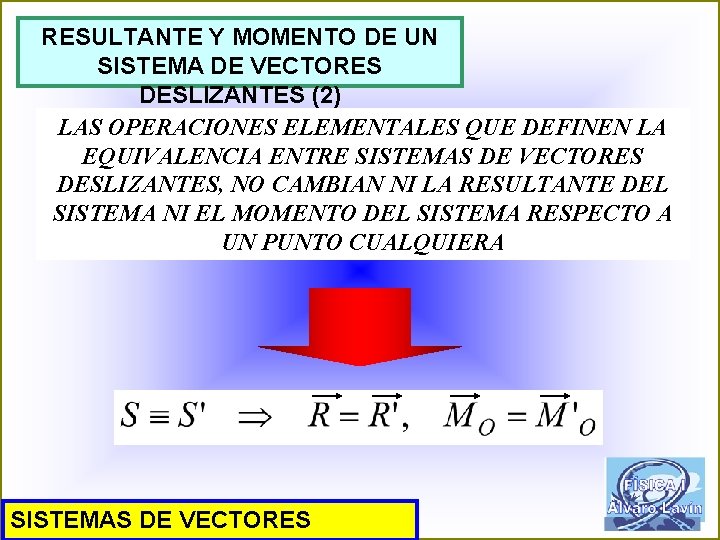
RESULTANTE Y MOMENTO DE UN SISTEMA DE VECTORES DESLIZANTES (2) LAS OPERACIONES ELEMENTALES QUE DEFINEN LA EQUIVALENCIA ENTRE SISTEMAS DE VECTORES DESLIZANTES, NO CAMBIAN NI LA RESULTANTE DEL SISTEMA NI EL MOMENTO DEL SISTEMA RESPECTO A UN PUNTO CUALQUIERA SISTEMAS DE VECTORES

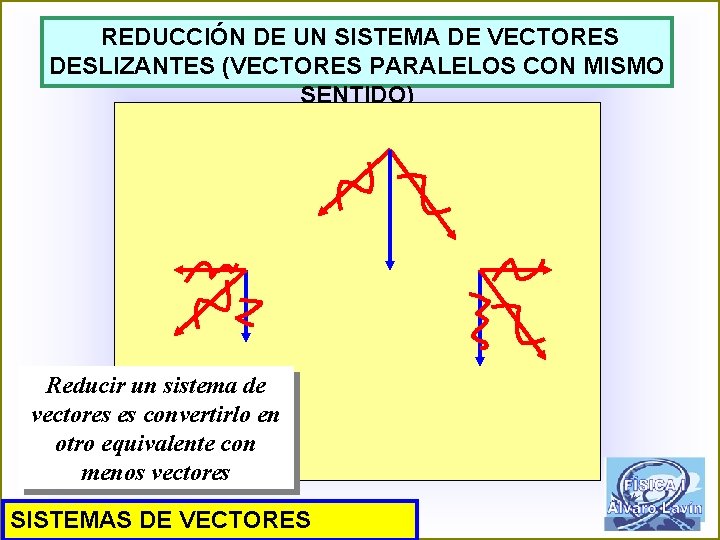
REDUCCIÓN DE UN SISTEMA DE VECTORES DESLIZANTES (VECTORES PARALELOS CON MISMO SENTIDO) Reducir un sistema de vectores es convertirlo en otro equivalente con menos vectores SISTEMAS DE VECTORES

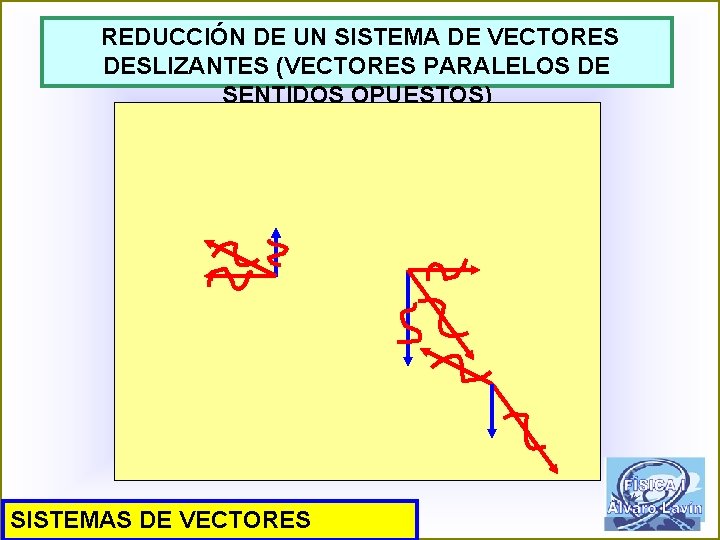
REDUCCIÓN DE UN SISTEMA DE VECTORES DESLIZANTES (VECTORES PARALELOS DE SENTIDOS OPUESTOS) SISTEMAS DE VECTORES

PAR DE VECTORES b A’ A a O Un par tiene resultante nula y momento independiente del punto con respecto al cual lo calculemos SISTEMAS DE VECTORES Un par son dos vectores de mismo módulo, sentidos opuestos y rectas soporte paralelas

EQUIVALENCIA DE PARES DE VECTORES (1) -b A -a B B’ a A’ b -a B -b A A’ b a SISTEMAS DE VECTORES B’

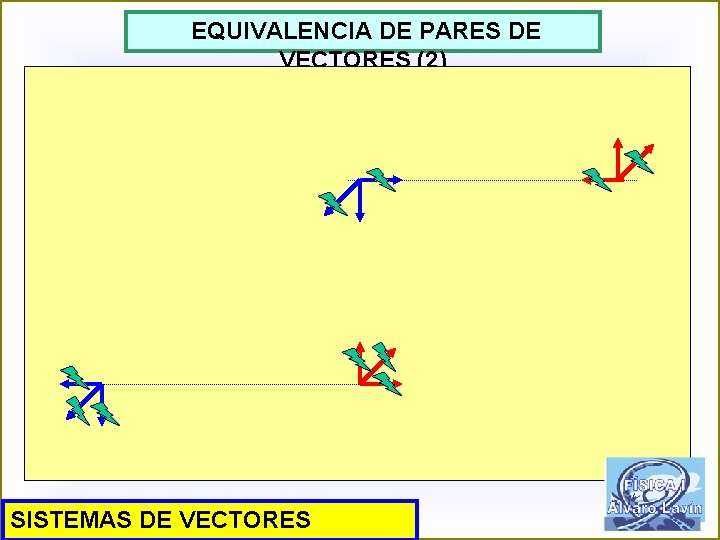
EQUIVALENCIA DE PARES DE VECTORES (2) SISTEMAS DE VECTORES

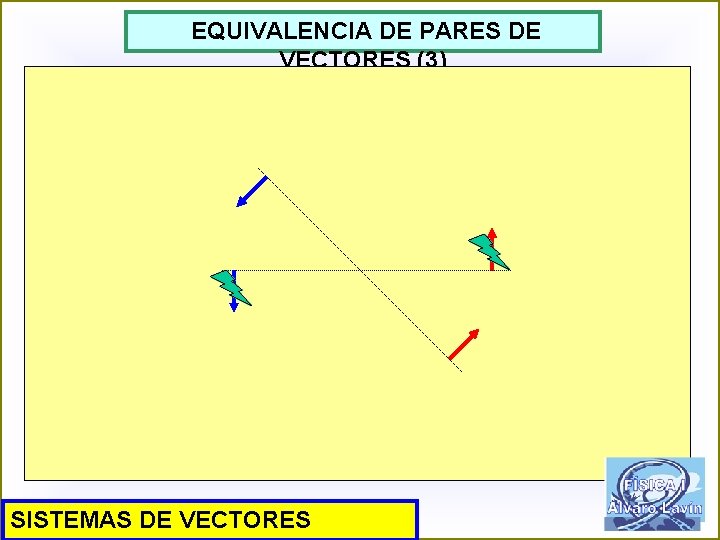
EQUIVALENCIA DE PARES DE VECTORES (3) SISTEMAS DE VECTORES

EQUIVALENCIA DE PARES DE VECTORES (4) SISTEMAS DE VECTORES

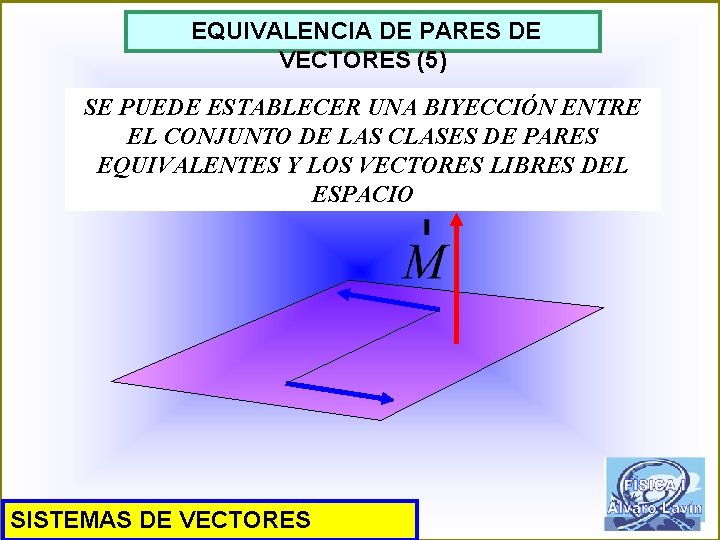
EQUIVALENCIA DE PARES DE VECTORES (5) SE PUEDE ESTABLECER UNA BIYECCIÓN ENTRE EL CONJUNTO DE LAS CLASES DE PARES EQUIVALENTES Y LOS VECTORES LIBRES DEL ESPACIO SISTEMAS DE VECTORES

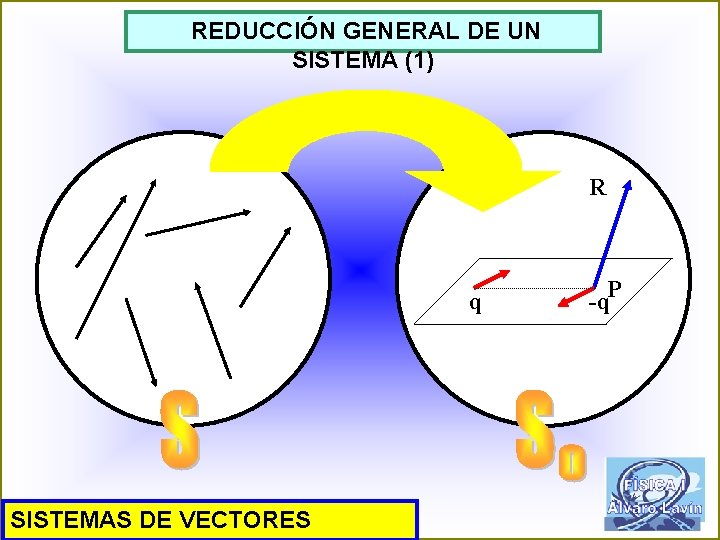
REDUCCIÓN GENERAL DE UN SISTEMA (1) R q SISTEMAS DE VECTORES -q. P

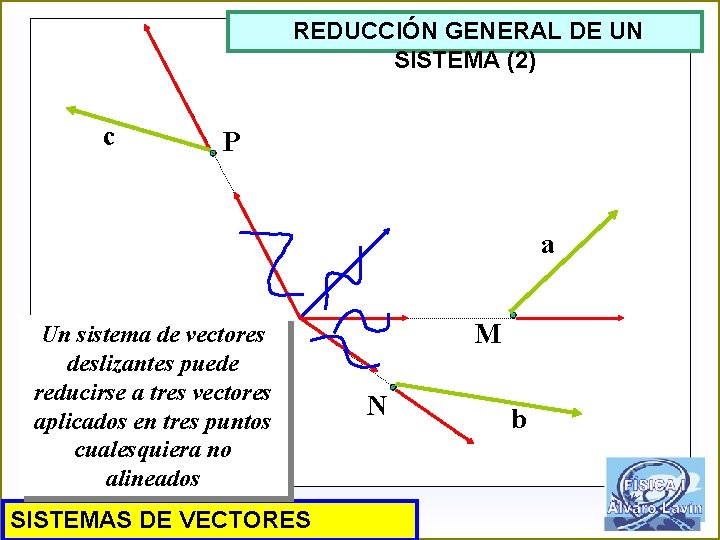
REDUCCIÓN GENERAL DE UN SISTEMA (2) c P a Un sistema de vectores deslizantes puede reducirse a tres vectores aplicados en tres puntos cualesquiera no alineados SISTEMAS DE VECTORES M N b

REDUCCIÓN GENERAL DE UN SISTEMA (3) c p b 1 P a 1 b 2 a 2 N b b 1 Un sistema de vectores b 2 deslizantes puede Q reducirse a dos vectores cuyas rectas soporte se cruzan SISTEMAS DE VECTORES M a a 1 q a 2

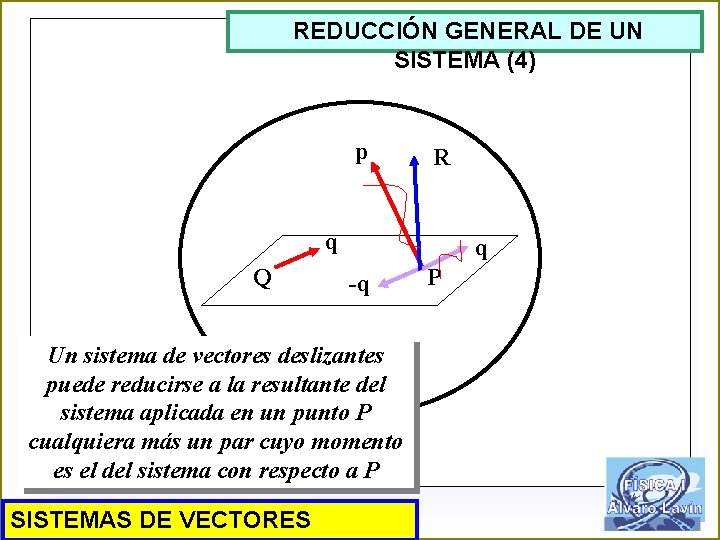
REDUCCIÓN GENERAL DE UN SISTEMA (4) p R q Q q -q Un sistema de vectores deslizantes puede reducirse a la resultante del sistema aplicada en un punto P cualquiera más un par cuyo momento es el del sistema con respecto a P SISTEMAS DE VECTORES P

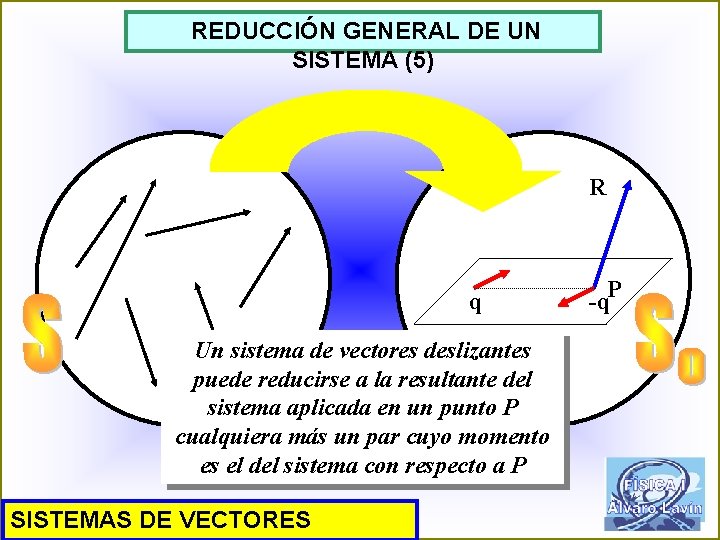
REDUCCIÓN GENERAL DE UN SISTEMA (5) R q Un sistema de vectores deslizantes puede reducirse a la resultante del sistema aplicada en un punto P cualquiera más un par cuyo momento es el del sistema con respecto a P SISTEMAS DE VECTORES -q. P

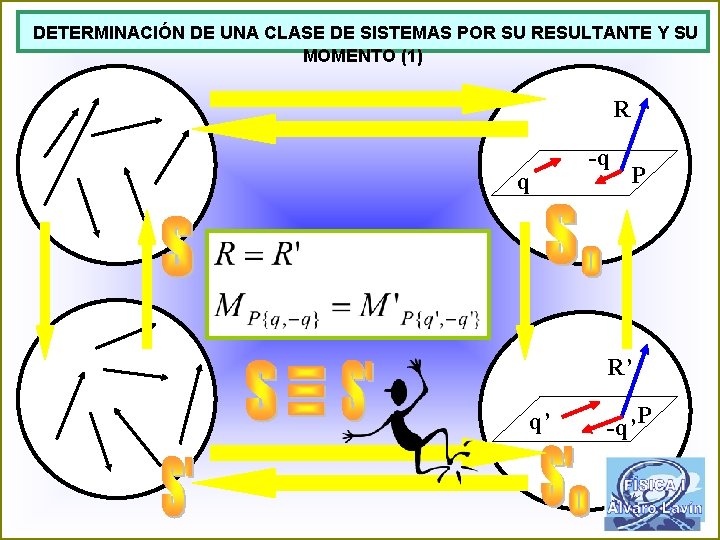
DETERMINACIÓN DE UNA CLASE DE SISTEMAS POR SU RESULTANTE Y SU MOMENTO (1) R q -q P R’ q’ -q’P

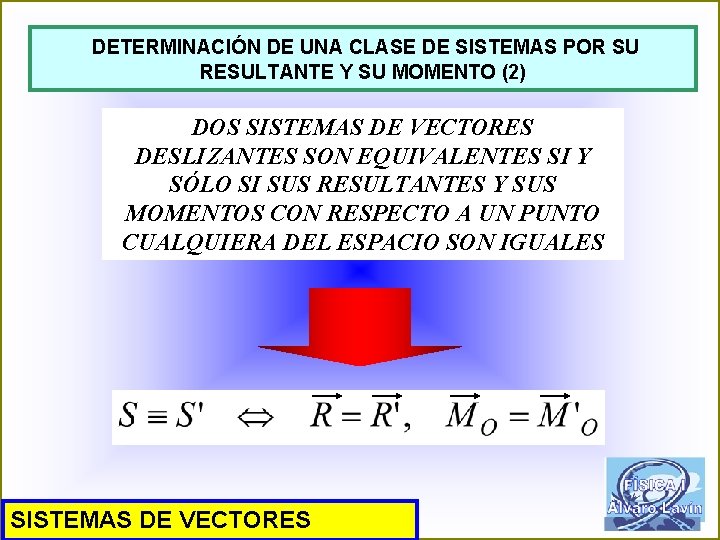
DETERMINACIÓN DE UNA CLASE DE SISTEMAS POR SU RESULTANTE Y SU MOMENTO (2) DOS SISTEMAS DE VECTORES DESLIZANTES SON EQUIVALENTES SI Y SÓLO SI SUS RESULTANTES Y SUS MOMENTOS CON RESPECTO A UN PUNTO CUALQUIERA DEL ESPACIO SON IGUALES SISTEMAS DE VECTORES

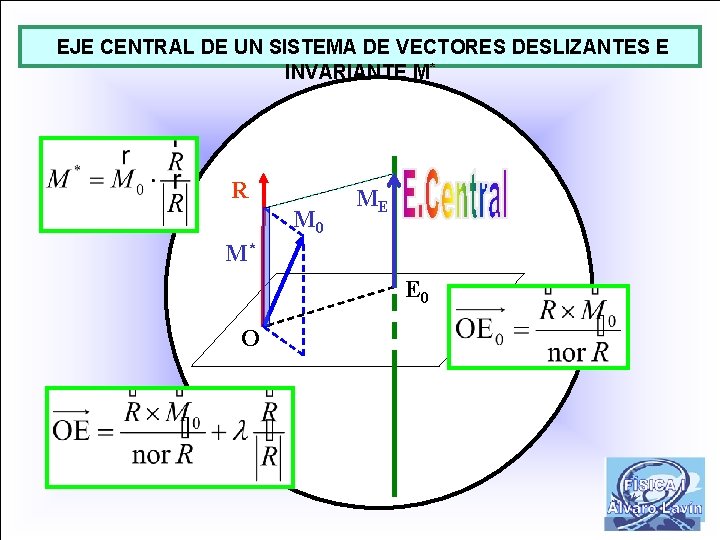
EJE CENTRAL DE UN SISTEMA DE VECTORES DESLIZANTES E INVARIANTE M* EJE CENTRAL DE UN SISTEMA DE VECTORES DESLIZANTES ES EL LUGAR GEOMÉTRICO DE LOS PUNTOS CON RESPECTO LOS CUALES EL MOMENTO CENTRAL DEL SISTEMA TIENE LA DIRECCIÓN DE LA RESULTANTE EJE CENTRAL DE UN SISTEMA DE VECTORES DESLIZANTES ES EL LUGAR GEOMÉTRICO DE LOS PUNTOS CON RESPECTO LOS CUALES EL MOMENTO CENTRAL DEL SISTEMA ES DE MÓDULO MÍNIMO

EJE CENTRAL DE UN SISTEMA DE VECTORES DESLIZANTES E INVARIANTE M* R M 0 ME M* E 0 O

CLASIFICACIÓN DE LOS SISTEMAS DE VECTORES DESLIZANTES S 11 (R 0, M* 0) Máxima reducción a la resultante y un par Condición eje central: R x ME = 0 S 01 (R=0, M 0) Máxima reducción a un par aplicado en cualquier punto del espacio Eje central no definido S 10 (R 0, M*=0) Máxima reducción a la resultante en un punto del eje central Condición eje central: ME = 0 S 00 (R=0, M=0)

• la resultante y el momento del sistema con respecto al origen de coordenadas • las coordenadas cartesianas de un punto del eje central que pertenezca al plano z=4 …es el vector de posición de un punto del eje central en el plano perpendicular a la resultante que pasa por el origen de coordenadas (plano xy) … …el eje central pasa por ese punto y es paralelo al eje z; por tanto, el punto solicitado es… • proponga un sistema reducido con el menor número posible de vectores Como la proyección del momento sobre la resultante es cero, el sistema es reducible a la resultante aplicada en cualquier punto del eje central.

Un sistema de vectores deslizantes tiene como resultante y como momento respecto al origen Determinar para que el punto A(2, 1, 0) sea del eje central y expresar la ecuación del eje central …por tanto, con respecto a los puntos del eje central el momento del sistema es nulo

• la resultante y el momento del sistema con respecto al origen de coordenadas • Ecuación del eje central del sistema de vectores …es el vector de posición de un punto del eje central en el plano perpendicular a la resultante que pasa por el origen de coordenadas …el eje central puede expresarse como… • proponga un sistema reducido con el menor número posible de vectores Como la proyección del momento sobre la resultante es cero, el sistema es reducible a la resultante aplicada en cualquier punto del eje central.

Se da el sistema de vectores deslizantes cuyas rectas soporte pasan por A 1(0, 3, 0) y A 2(1, 0, 0). Determinar un sistema equivalente al dado con el menor número posible de vectores, indicando su recta soporte. Ejerc. 2 Exam. Sep. 2009

Un sistema de vectores deslizantes tiene como resultante y como momento respecto al origen Determinar para que el punto A(4, 4, 0) sea del eje central. Ejerc. 3 Exam. Feb. 2009

• la resultante y el momento del sistema con respecto al origen de coordenadas • Ecuación del eje central del sistema de vectores …es el vector de posición de un punto del eje central en el plano perpendicular a la resultante que pasa por el origen de coordenadas …el eje central puede expresarse como… • Justifique si el sistema de vectores puede reducirse a un solo vector o no Como la proyección del momento sobre la resultante es diferente de cero, el sistema no es reducible a un solo vector


BIBLIOGRAFÍA ANÁLISIS VECTORIAL, J. J. SCALA Lección 4: Vectores deslizantes y ligados FÍSICA GENERAL I, A. M. Sánchez Pérez Secciones 4. 11 y 4. 12
 Versin final
Versin final Vectores deslizantes
Vectores deslizantes 35000x24
35000x24 Orden del 16 de junio de 2014
Orden del 16 de junio de 2014 Fiesta 13 de junio
Fiesta 13 de junio 12 de junio inmaculado corazon de maria
12 de junio inmaculado corazon de maria Feliz jueves 10 de junio
Feliz jueves 10 de junio Feliz cumpleaños a los nacidos en junio
Feliz cumpleaños a los nacidos en junio Vamos a perú ___ las vacaciones.
Vamos a perú ___ las vacaciones. Que se festeja hoy 5 de junio
Que se festeja hoy 5 de junio Formula de snell
Formula de snell Feliz miercoles primero de junio
Feliz miercoles primero de junio Poema junio octavio paz
Poema junio octavio paz Vector coplanares
Vector coplanares Norma euclidiana matlab
Norma euclidiana matlab Nomenclatura de vectores
Nomenclatura de vectores Vectores
Vectores Calculadora
Calculadora Ciencia que estudia los vectores
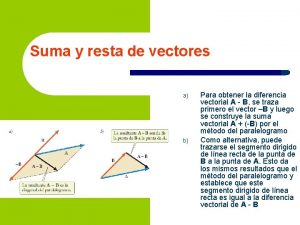
Ciencia que estudia los vectores Suma y resta de vectores
Suma y resta de vectores Radianes a grados
Radianes a grados Distancia entre dos vectores
Distancia entre dos vectores Sean los vectores
Sean los vectores Qué son las enfermedades transmitidas por vectores
Qué son las enfermedades transmitidas por vectores Vectores en coordenadas geográficas
Vectores en coordenadas geográficas Porque los vectores no se suman aritméticamente
Porque los vectores no se suman aritméticamente Vectores i y j
Vectores i y j Aplicacion de estructuras de datos vectores y matrices
Aplicacion de estructuras de datos vectores y matrices Base normada
Base normada Vectores y matrices en java
Vectores y matrices en java Como se representa la fuerza
Como se representa la fuerza Versores i j k
Versores i j k Suma y resta de vectores
Suma y resta de vectores Definicion fuerza elastica
Definicion fuerza elastica Fisica mediciones y vectores
Fisica mediciones y vectores Vectores iguales
Vectores iguales Vectores
Vectores Stata vector
Stata vector Ordenar
Ordenar Vector unitario formula
Vector unitario formula Ixi=jxj=kxk=
Ixi=jxj=kxk= Solucion general
Solucion general Cuando usar seno y coseno en vectores
Cuando usar seno y coseno en vectores Inverso aditivo
Inverso aditivo Tipos de sistema de referencia
Tipos de sistema de referencia Valor propio dominante
Valor propio dominante Conclusiones de vectores
Conclusiones de vectores Elaborado por
Elaborado por Metodo del paralelogramo
Metodo del paralelogramo Dado los vectores
Dado los vectores R
R Vectores
Vectores Produto escalar
Produto escalar Como sacar el angulo entre dos vectores
Como sacar el angulo entre dos vectores Producto entre vectores
Producto entre vectores Vectores deslizantes y libres
Vectores deslizantes y libres Vectores deslizantes
Vectores deslizantes Hallar vectores
Hallar vectores Sean los vectores
Sean los vectores Ejemplo de arreglo unidimensional
Ejemplo de arreglo unidimensional Suma de vectores polares
Suma de vectores polares Middleware vantagens e desvantagens
Middleware vantagens e desvantagens Sistemas de bronfenbrenner
Sistemas de bronfenbrenner Sistemas smp
Sistemas smp Que son los sistemas tecnicos como producto cultural
Que son los sistemas tecnicos como producto cultural Sistemas categoriales observacion
Sistemas categoriales observacion Tendencias futuras de los sistemas de información
Tendencias futuras de los sistemas de información Sistemas uni
Sistemas uni Que es un sistema de ecuacion
Que es un sistema de ecuacion