Anlisis Matemtico III PRIMERA PARTE Funciones SEGUNDA PARTE




















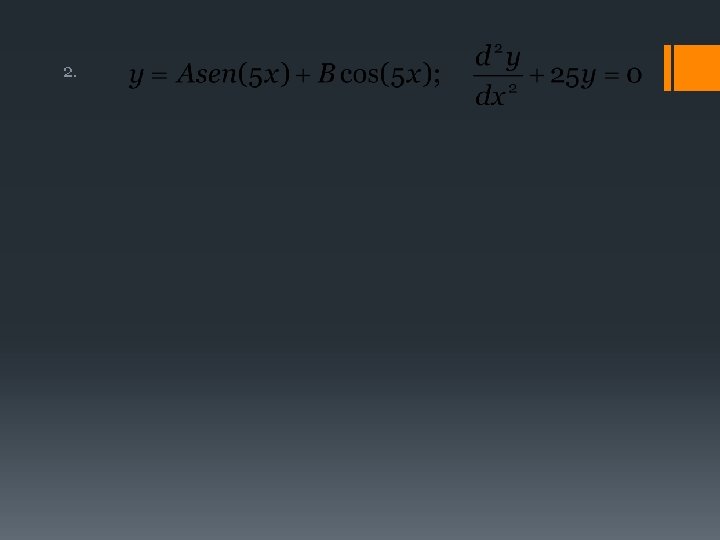
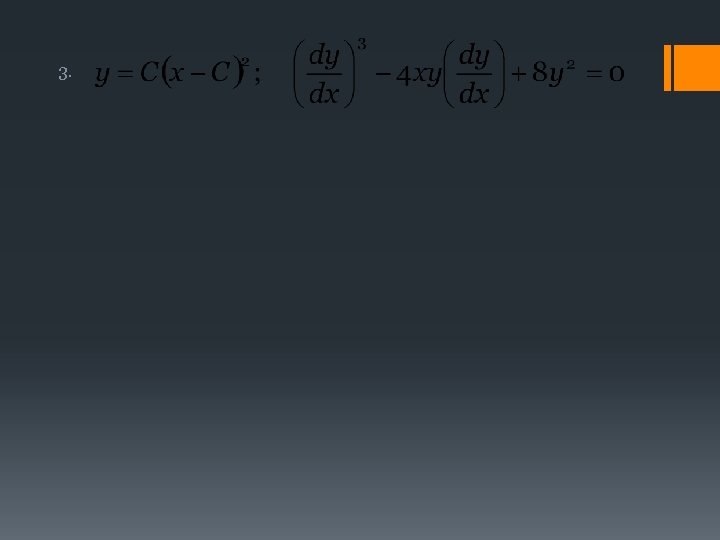









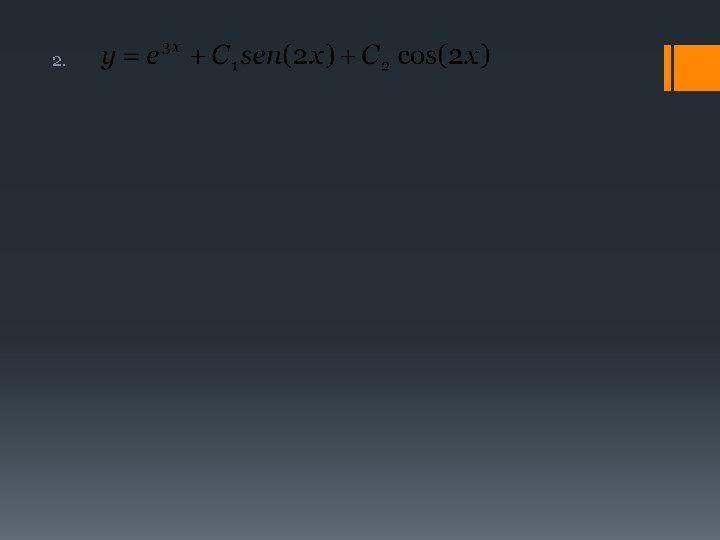












- Slides: 44

Análisis Matemático III • PRIMERA PARTE Funciones • SEGUNDA PARTE Integrales • TERCERA PARTE Ecuaciones diferenciales • CUARTA PARTE Método para resolver una ecuación diferencial

Ecuaciones Diferenciales

III. 1 INTRODUCCIÓN Definición Una ecuación diferencial (ED) es una ecuación que involucra derivadas de una función desconocida de una o varias variables. Ejemplo Las siguientes expresiones son ejemplos de ED’s: Conocida como Ley de Crecimiento Exponencial

III. 1 INTRODUCCIÓN En base a la definición anterior se tiene que: a) Si la función desconocida depende de solo una variable la ecuación se llama Ecuación Diferencial Ordinaria. b) Si la función desconocida depende de más de una variable la ecuación se llama Ecuación Diferencial Parcial.

III. 1 INTRODUCCIÓN Las ecuaciones diferenciales pueden clasificarse por su orden y grado. Orden El orden de una ecuación diferencial es el orden de la derivada mas alta que aparece en la ecuación. Ejemplo Determinar el orden de las ecuaciones diferenciales:

III. 1 INTRODUCCIÓN Solución La ecuación diferencial: Es de primer orden dado que la derivada mas alta que figura en la ecuación diferencial es la primera derivada. La ecuación diferencial: Es de segundo orden dado que la derivada más alta que figura en la ecuación diferencial es la de la segunda derivada.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clase Determinar el orden de las siguientes ecuaciones: a) b)

III. 1 INTRODUCCIÓN Grado El grado de una ecuación diferencial es el grado algebraico de su derivada de mayor orden, es decir, el grado de una ecuación diferencial es la potencia a la que esta elevada la deriva que nos dio el orden de la ecuación diferencial. Ejemplo El grado de la ecuación diferencial es: de tercer grado, dado que la primera derivada está elevada cubo.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clase Determinar el grado de las siguientes ecuaciones: a) b)

III. 1 INTRODUCCIÓN NOTA: cuando alguna derivada este dentro de un radical o en polinomio, el cual este elevado a una potencia fraccionaria, tendremos que eliminar dicho radical para después determinar el grado de la ecuación diferencial.

III. 1 INTRODUCCIÓN Ejercicios para resolver en clases Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) b)

III. 1 INTRODUCCIÓN Ejercicios para resolver en clases Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) b)

III. 1 INTRODUCCIÓN Ejercicios de Tarea Determinar el orden y grado de las siguientes ecuaciones diferenciales: a) c) d) b)

III. 2 SOLUCIÓN DE UNAED Una solución de una ED es cualquier función que satisface la ED, este es, la reduce a una identidad. Ejemplo La funciónuna solución es definida la de por ecuación diferencial: puesto que: y al sustituir en la ED se obtiene una identidad

III. 2 SOLUCIÓN DE UNAED Una solución particular de una ED es toda solución obtenida asignando valores específicos a las constantes que intervienen en la solución general. Ejemplo Verificar que y=Cx 3 es solución de la ecuación diferencial Hallar la solución particular sujeta a la condición inicial:

III. 2 SOLUCIÓN DE UNAED Solución Derivando y=Cx 3 tenemos que y’=3 Cx 2, luego, sustituyendo en la ED: de esta manera y=Cx 3 es solución de la ED. Para obtener la solución particular, apliquemos la condición inicial y(-3)=2 en la solución general esto es: La solución particular es:

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Para comprobar que una ecuación es o no la solución de una ecuación dada, se aplica el siguiente método: Método 1. Observemos que derivada o derivadas aparecen en la ecuación diferencial. 2. Estas derivadas las encontramos al derivar la ecuación que se supone solución. 3. La ecuación será solución cuando al sustituir el valor de las derivadas encontradas (paso 2) dentro de la ecuación diferencial, aparezca una identidad a=a (donde aєR) al reducir la ecuación ya sustituida.

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejemplo Comprobar que la y=x 2+C no es solución de la ecuación diferencial Solución 1. Observando la ecuación diferencial vemos que aparece una derivada por lo tanto, encontramos su valor derivando la supuesta solución. 2. Derivando y=x 2+C tenemos

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Solución 3. Sustituyendo el valor de la derivada encontrada en la ecuación diferencial tenemos: Por lo tanto y=x 2+C si es solución de la ecuación diferencial

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejercicios para resolver en clase Determine si cada ecuación es solución o no de la ecuación diferencial dada: 1.
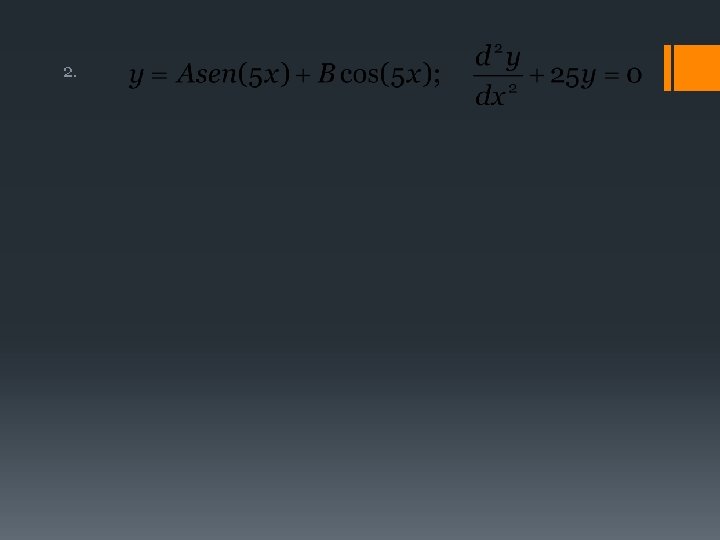
2.
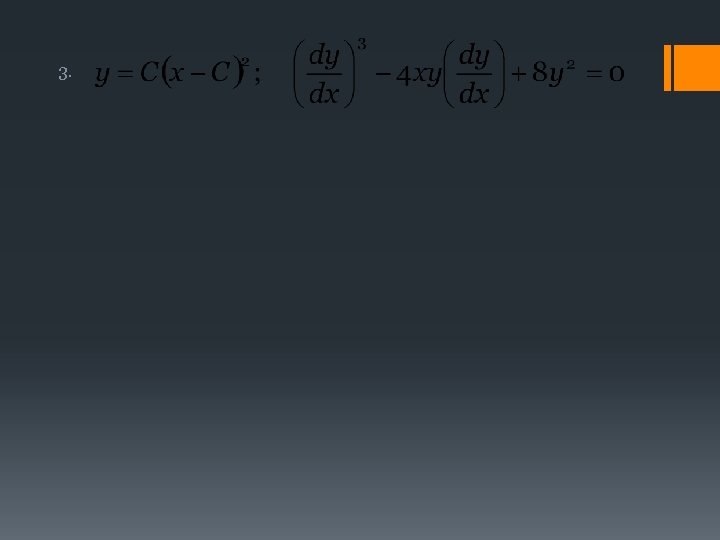
3.

III. 2. 1 COMPROBACIÓN DE LASOLUCIÓN DE UNAED Ejercicios de tarea Determine si cada ecuación es solución o no de la ecuación diferencial dada: 1. 2. 3.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Para obtener la ED a partir de su solución general, aplicaremos el siguiente método: 1. Observemos el número de constantes de integración que aparecen en la solución general dada. 2. Derivemos la solución general tantas veces como el número de constantes de integración aparezcan en ella. En otras palabra, si la solución general tienen n constantes de integración diferentes, entonces derivaremos n veces tal solución.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL 3. Tomando en cuenta el resultado de la última derivada obtenida, se nos pueden presentar los siguientes casos: a) Si en la última derivada ya no aparecen constantes de integración, esta será la ED que de la solución general dada. b) Si la última derivada contiene constantes de integración, habrá que eliminarlas, pudiendo utilizar para esto, las ecuaciones de las derivadas encontradas, así como también la solución general dada. En la ED NO deben aparecer constantes de integración.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejemplo Encuentre la ED cuya solución general es y=x 2+C

Solución Observemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y=x 2+C. Así Como en esta derivada no aparecen constantes de integración, quiere decir que esta es la ED de la solución general presentada al inicio.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejemplo Encuentre la ED cuya solución general es y=Cx 2

Solución Observemos que sólo aparece una constante de integración, de manera que derivamos una sola vez la solución general y=Cx 2. Así Se va a despejar C de la solución general y se sustituye el valor encontrado en la ED.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Solución Por lo tanto: Es la ED de la solución general puesto que ya no aparecen constantes de integración.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejercicios para resolver en clase Encuentre la ED de las siguientes soluciones generales 1.
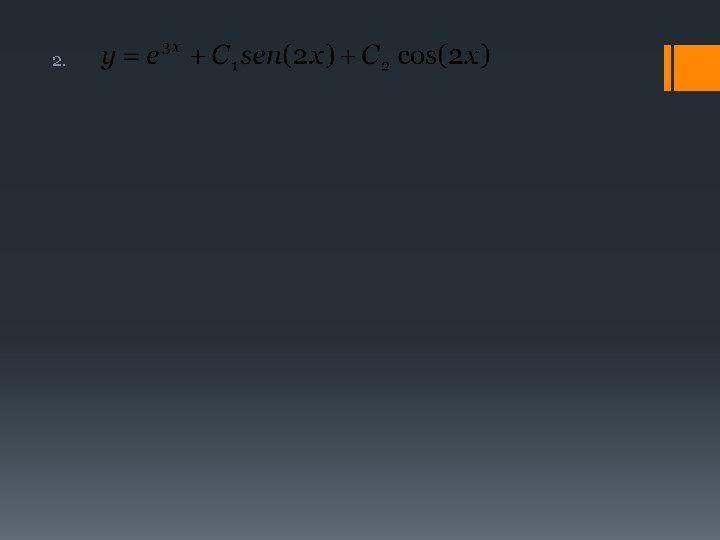
2.

III. 3 OBTENCIÓN DE LAED A PARTIR DE LA SOLUCIÓN GENERAL Ejercicios de tarea Encuentre la ED de las siguientes soluciones generales 1. 2.

Métodos para resolver una ecuación diferencial Método de separación de variables. La idea más simple de los procedimientos de solución es reescribir la ecuación como una ecuación de variables separadas: Donde f(y) es una función exclusivamente de y y g(x) es una función exclusivamente de x. Esta ecuación se resuelve integrando a ambos lados:

Ejemplo 1: Resolver la ecuación

Ejemplo 2: Resolver la ecuación

ED exactas Definición: Sean funciones definidas en cierto dominio ecuación de la forma Se llama una diferencial exacta. La ecuación diferencial Es exacta si: Y también se tiene que dos. La

Donde la solución queda dada por:


Ejemplo:

Ejemplo:

ED Lineales de 1 er orden Las ED de la forma Se denominan ED Lineales. 1. Caso Homogéneo (q(x)=0): Es decir, se resuelven usando variación de la constante c de la solución donde

Ejemplo : Resolver la ecuación

2. Caso No Homogéneo (q(x)≠ 0): Se resuelven usando un factor integrante.
 Qué es la desinencia del verbo
Qué es la desinencia del verbo Que países participaron en la primera guerra mundial
Que países participaron en la primera guerra mundial No hay una segunda oportunidad para la primera impresión
No hay una segunda oportunidad para la primera impresión Integrales eulerianas
Integrales eulerianas Dependencia multivaluada base de datos
Dependencia multivaluada base de datos 2 persona
2 persona Segunda persina
Segunda persina Primera persona segunda persona y tercera persona
Primera persona segunda persona y tercera persona Primera forma normal base de datos
Primera forma normal base de datos Cuantas son las venidas de cristo
Cuantas son las venidas de cristo Humunculo motor
Humunculo motor Ejemplos de verbos
Ejemplos de verbos Marcha helicopoda
Marcha helicopoda Conjugacion del verbo ir en español
Conjugacion del verbo ir en español Anlisis foda
Anlisis foda Fo maxi maxi
Fo maxi maxi Anlisis de riesgos
Anlisis de riesgos Estrategias fo maxi maxi
Estrategias fo maxi maxi Amenazas de una empresa ejemplos
Amenazas de una empresa ejemplos Anlisis financiero
Anlisis financiero Preguntas para el bautismo segunda parte
Preguntas para el bautismo segunda parte Hamlet act iii scene ii
Hamlet act iii scene ii Corresponde a la primera parte, excepto *
Corresponde a la primera parte, excepto * Este parte aquele parte
Este parte aquele parte Como multiplicar decimales
Como multiplicar decimales Missa parte por parte
Missa parte por parte Te invitamos a ser parte o hacer parte
Te invitamos a ser parte o hacer parte Leyes de newton
Leyes de newton Universidad nacional de tumbes segunda especialidad
Universidad nacional de tumbes segunda especialidad Segunda unidad de ingles
Segunda unidad de ingles Tercera etapa de goya
Tercera etapa de goya Um casal ambos polidáctilos
Um casal ambos polidáctilos Transistores de la segunda generacion
Transistores de la segunda generacion Sistema de segunda ordem
Sistema de segunda ordem Fnbc
Fnbc 5 características de la revolución industrial
5 características de la revolución industrial Himno nacional de costa rica estrofas
Himno nacional de costa rica estrofas 2 corintios 13: 5
2 corintios 13: 5 Dcl
Dcl Tercera forma normal
Tercera forma normal Cefalosporina de primera generacion
Cefalosporina de primera generacion Primeira segunda e terceira conjugação
Primeira segunda e terceira conjugação 2 reis 4
2 reis 4 Segunda persona
Segunda persona Conclusiones de la segunda guerra mundial
Conclusiones de la segunda guerra mundial