Integrales Impropias 1 E T S I TOPOGRAFA

Integrales Impropias 1

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia Unidad Docente de Matemáticas Salir

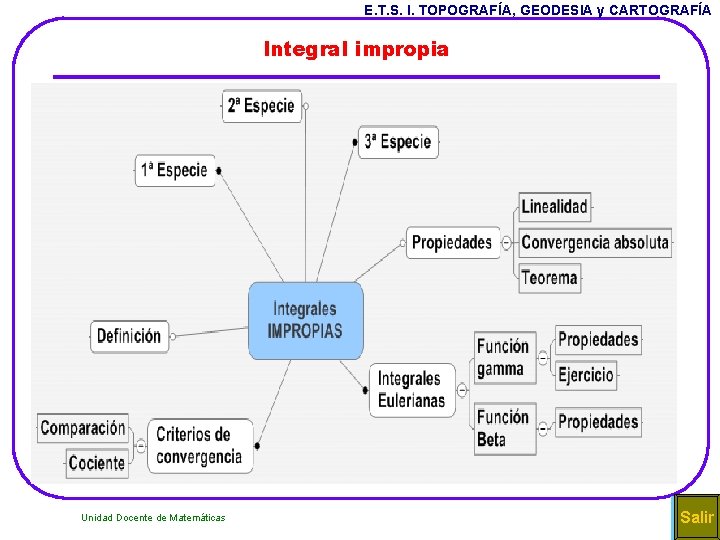
E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia La integral es una integral impropia si se da uno de los siguientes casos: a) a ó b ó ambas son infinitos b) La función f (x) se hace infinita (no acotada) en uno ó más puntos de [a, b] • En el primer caso se llama integral impropia de 1ª especie. • En el segundo caso integral impropia de 2ª especie. • Si ocurren ambos casos a la vez se llama integral impropia de 3ª especie. Unidad Docente de Matemáticas 3

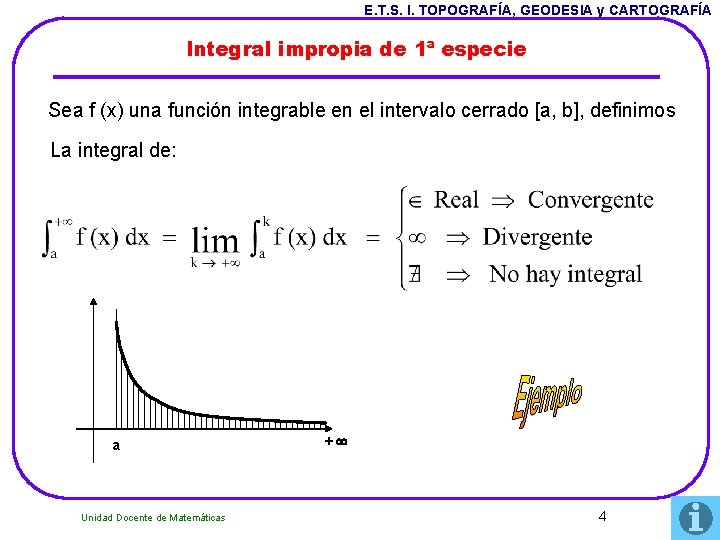
E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia de 1ª especie Sea f (x) una función integrable en el intervalo cerrado [a, b], definimos La integral de: a Unidad Docente de Matemáticas + 4

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia de 1ª especie Análogamente: Si a → - y b → . Entonces: Unidad Docente de Matemáticas 5

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Ejemplo Integral impropia 1ª especie Calcular: Unidad Docente de Matemáticas 6

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia de 2ª especie Tal que f (x) tiene una discontinuidad en [a, b] Casos que se pueden presentar: a) Si f (x) continua en [a, b), pero para x = b, f (x) → . Se define: = Unidad Docente de Matemáticas Siempre que exista el límite 7

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Ejemplo Integral impropia 2ª especie Calcular: Unidad Docente de Matemáticas 8

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia de 2ª especie b) Si f (x) continua en (a, b], pero para x = a, f (x) → . Se define: = Siempre que exista el límite c) Si f (x) continua en [a, b], pero para x = c [a, b] , f (x) → Siempre que ambos límites existan Unidad Docente de Matemáticas 9

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integral impropia de 3ª especie Se tiene una integral que contiene los dos tipos : 1ª especie y 2ª especie. Un caso puede ser el siguiente: ya que: b → y además para x = a, f (x) → - . Luego: Unidad Docente de Matemáticas 10

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Propiedades de las integrales impropias Nos referiremos a las integrales impropias de 1ª especie, pero son válidas para las de 2ª y 3ª especie. 1. Sea f(x) y g(x) dos funciones continuas en [a, ) y supongamos que convergen, entonces I= es convergente ∀ y R. Verificándose I = Unidad Docente de Matemáticas 11

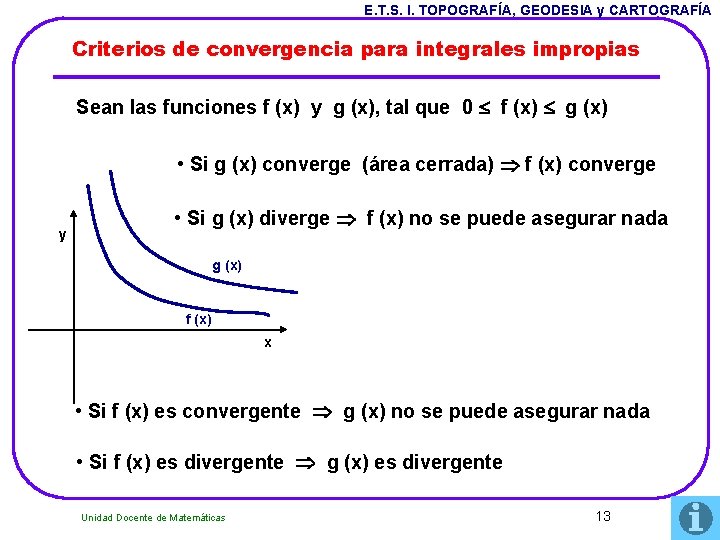
E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Criterios de convergencia para integrales impropias Sean las funciones f (x) y g (x), tal que 0 f (x) g (x) • Si g (x) converge (área cerrada) f (x) converge y • Si g (x) diverge f (x) no se puede asegurar nada g (x) f (x) x • Si f (x) es convergente g (x) no se puede asegurar nada • Si f (x) es divergente g (x) es divergente Unidad Docente de Matemáticas 13

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Criterios de convergencia para integrales impropias Criterio del cociente o de comparación en el límite Sean f (x) y g (x) tales que 0 ≤ f (x) ; g (x) ≥ 0 x ≥ a Si ó Si Si Unidad Docente de Matemáticas 14

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Criterios de convergencia para integrales impropias Corolario Sea f (x) ≥ 0 x ≥ a , entonces, siendo Unidad Docente de Matemáticas 15

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Criterios de convergencia para integrales impropias Sabemos: Unidad Docente de Matemáticas 16

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integrales Eulerianas: Función gamma de Euler 1. Función gamma de Euler Esta función integral viene definida y representada: donde para p >0 es convergente y se denomina integral de Euler de primera especie. Unidad Docente de Matemáticas 17

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Integrales Eulerianas: Función gamma de Euler (Ejemplo) Calculamos gamma de 1, es decir, Unidad Docente de Matemáticas 18

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Propiedades de la función gamma 1. (p+1) = p (p) con 0<p Demostración: 2. Si p N y p ≥ 1, entonces (p) = (p-1) 3. (p) (1 -p) = 4. = Unidad Docente de Matemáticas Demostración: para 0 < p < 1 Demostración: 19

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA 1. Propiedad de la función gamma 1. (p+1) = p (p) con 0<p Demostración: Sabemos que: Resolvemos esta integral por partes: Unidad Docente de Matemáticas 20

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA 2. Propiedad de la función gamma 2. Si p N y p ≥ 1, entonces (p) = (p-1) Demostración: Por la propiedad anterior: (p+1) = p (p) = (p-1) = (p-2) = (p-3) Así sucesivamente …… …… …… (3) = 2 (2) = 1 (1) = 1 Sustituyendo cada expresión en la anterior queda: (p) = (p-1)(p-2)(p-3)… 3. 2. 1 = (p-1)! Unidad Docente de Matemáticas 21

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA 4. Propiedad de la función gamma 4. = Demostración: Por propiedad anterior tenemos que: 3. (p) (1 -p) = para 0 < p < 1 En particular para p=1/2, resulta: Unidad Docente de Matemáticas 22

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Función Beta de Euler 1. Función beta de Euler Esta función integral viene definida y representada: donde para p, q >0 es convergente y se denomina integral de Euler de segunda especie. Unidad Docente de Matemáticas 23

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Función Beta de Euler (Ejemplo) Calcular: Sabemos que: Realizamos el cambio: Si x=0, entonces sent=-1, por tanto Si x=1, entonces sent=1, por tanto Unidad Docente de Matemáticas 24

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Propiedades de la función beta 1. (p, q) = (q, p) 2. (p, q) = Demostración: 3. para p, q > 0 Unidad Docente de Matemáticas 25

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA 1. Propiedad de la función beta 1. (p, q) = (q, p) Demostración: Con el cambio de variable 1 -x = z tenemos que: x = 1 -z y por tanto dx = - dz Si x=0, entonces z=1 Si x=1, entonces z=0 Unidad Docente de Matemáticas 26

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA 2. Propiedad de la función beta 2. (p, q) = Demostración: Con el cambio de variable x = (sent)2 tenemos que: 1 -x = 1 -(sent)2 = (cost)2 y, por tanto, dx = 2 sent cost dt Si x=0, entonces sent = 0, luego t = 0 Si x=1, entonces sent = 1, luego t = Unidad Docente de Matemáticas 27

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Ejercicios de aplicación de las integrales Eulerianas I. - Calcular, si es convergentes, la integral siguiente: = Cambio de variable: p– 1=2 Integral gamma Unidad Docente de Matemáticas 28

E. T. S. I. TOPOGRAFÍA, GEODESIA y CARTOGRAFÍA Ejercicios de aplicación de las integrales Eulerianas II. - Calcular la integral siguiente: Identificamos la integral como una beta: Parámetros: Y por la propiedad 3: Unidad Docente de Matemáticas 29