CAP 6 PROGRAMACIN LINEAL Programacin Lineal tiene las

CAP. 6 PROGRAMACIÓN LINEAL

Programación Lineal tiene las siguientes aplicaciones típicas: - Un fabricante desea elaborar un programa de producción y una política de inventarios que satisfaga la demanda del futuro, minimizarán la producción y costos de inventario. - Un analista financiero debe seleccionar un portafolios de inversión entre acciones y bonos, debe maximizar el retorno de la inversión.

Programación Lineal - - Un gerente de mercadotecnia desea determinar como asignar el presupuesto de publicidad entre varios medios alternativos , buscar la mezcla de medios para maximizar la efectividad de la publicidad. Una empresa tiene almacenes en diferentes ubicaciones , con una demanda específica determinar cuanto embarcar de cada almacén para cada cliente, minimizar los costos de transporte.

Naturaleza y estructura de los modelos matemáticos Variables y parámetros de decisión Restricciones Función Objetivo

de Problemas Una empresa dispone de 70 trabajadores con cualificaciones diferentes (Economistas, Ingenieros, Auxiliares Administrativos, etc. . ) a los que hemos de asignar 70 actividades también diferentes. Para decidir una determinada asignación de tareas deberíamos escoger de entre un total de 70! (Permutaciones de 70 elementos) aquella que maximiza el resultado final de la empresa. Como 70! es aproximadamente igual a 10100, aún revisando un 1 millón de asignaciones diferentes al segundo necesitaríamos aproximadamente 1087 años para revisar todas las asignaciones posibles. Este tipo de problemas requiere desarrollar modelos de programación matemática, otros métodos matemáticos, para llegar a algún tipo de conclusiones.

Características de la P. L. 1. Un único objetivo lineal a optimizar (maximizar o minimizar) 2. Unas variables de decisión que siempre son continuas y no negativas 3. Una o más restricciones lineales 4. Un conocimiento exacto de los parámetros y recursos utilizados en la construcción del modelo.

Formulación de Modelos Primero veremos como con la programación lineal se puede expresar matemáticamente. Ejemplo: Dos empresas Mineras extraen dos tipos diferentes de minerales, los cuales son sometidos a un proceso de trituración, con tres grados: alto , medio y bajo. Las compañías han firmado un contrato para proveer de mineral a una planta de fundición, cada semana, 12 toneladas de mineral de grado alto, 8 toneladas de grado medio y 24 toneladas de grado bajo. Cada una de las empresas tiene diferentes procesos de fabricación. Mina Coste por día (miles de $US. ) Producció(toneladas/día) Alto Medio Bajo X 180 6 3 4 Y 160 1 1 6 ¿Cuántos días a la semana debería operar cada empresa para cumplir el contrato con la planta de fundición?

Formulación matemática básica en un problema de I. O. Debemos buscar una solución que minimice el coste de producción de las empresas, sujeta a las restricciones impuestas por el proceso productivo así como el contrato con la planta de fundición. Traducción del problema en términos matemáticos 1. definir las variables 2. las restricciones 3. el objetivo

Formulación matemática básica en un Restricciones problema de I. O. Variables Representan las decisiones que puede tomar la empresa: Dx = número de días a la semana que la empresa X produce Dy= número de días a la semana que la empresa Y produce Notar que Dx 0 y Dy 0 Objetivo Como objetivo buscamos minimizar el coste Se recomienda primero plantear las restricciones con palabras antes de pasar a su formulación matemática Restricción 1. Refleja el balance entre las limitaciones productivas de la fábrica y el contrato con la planta de fundición Grado Alto 6 Dx+1 Dy 12 Medio 3 Dx+1 Dy 8 Bajo 4 Dx+6 Dy 24 Restricción 2. Días de trabajo disponibles a la semana Dx 5 y Dy 5

Formulación matemática básica en un problema de I. O. La representación completa del problema tomaría la siguiente forma: Minimizar 180 Dx+160 Dy Restriciones: 6 Dx+1 Dy 12 3 Dx+1 Dy 8 4 Dx+6 Dy 24 Dx 5, Dy 5 Dx 0, Dy 0

Algunas reflexiones • Hemos pasado de la definición del problema a su formulación matemática. • Error de especificación, el error más frecuente consiste en descuidar las limitaciones (restricciones, características de las variables, etc, ) En el ejemplo anterior: a) Todas las variables son continuas (admitimos fracciones de día) b) Existe un único objetivo (minimizar los costes) c) El objetivo y las restricciones son lineales Las tres consideraciones anteriores nos llevan a lo que denominamos un problema de Programación Lineal PL

Algunas reflexiones El ejercicio anterior plantea un PROBLEMA DE DECISIÓN Hemos tomado una situación real y hemos construido su equivalente matemático MODELO MATEMÁTICO Durante la formulación del modelo matemático nosotros consideramos el método cuantitativo que (esperanzadamente) nos permitirá resolver el modelo numéricamente ALGORITMO El algoritmo es un conjunto de instrucciones que siguiendo de manera gradual producen una solución numérica Llegamos a una nueva definición de I. O. Ciencia para la representación de problemas reales mediante modelos matemáticos que junto con métodos cuantitativos nos permiten obtener una solución numérica a los mismos

Dificultades de este tipo de enfoques: • Identificación del problema (debemos ignorar partes o tratar el problema entero) • Elección del modelo matemático adecuado así como el algoritmo adecuado para resolverlo (validación del algoritmo) • Dificultades en la implementación • Velocidad (costes) que supone llegar a una solución • Calidad de la solución • Consistencia de la solución

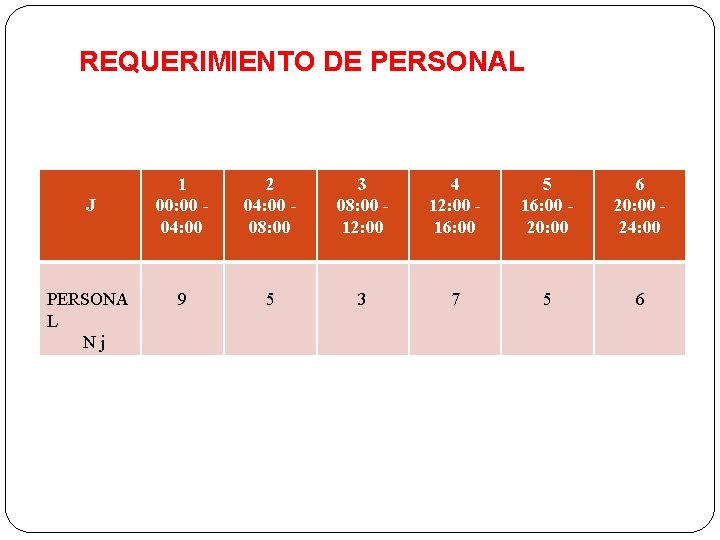
EJEMPLO DE ASIGNACION DE PERSONAL Farmacias Bolivia en sus 9 sucursales ha decidido ampliar su servicio a 24 horas, con la consiguiente necesidad de nuevo personal de atención al cliente. La gerencia de la Empresa ha estimado las necesidades mínimas de personal por tramos horarios para poder cubrir los requerimientos de los clientes que se presenten. Se definieron 6 tramos de 4 horas. La necesidad mínima de personal en cada tramo se indica en el Cuadro. Por otro lado, el departamento de recursos humanos ha informado a la gerencia que los contratos laborales han de ser de ocho horas seguidas, según normativa laboral, independientemente de los horarios de entrada y salida del personal. El problema es encontrar el número mínimo de personal necesario para cubrir la demanda.

REQUERIMIENTO DE PERSONAL J PERSONA L Nj 1 00: 00 - 04: 00 2 04: 00 - 08: 00 3 08: 00 - 12: 00 4 12: 00 - 16: 00 5 16: 00 - 20: 00 6 20: 00 - 24: 00 9 5 3 7 5 6

Formulación del problema En primer lugar, se tienen que definir las variables del modelo queremos desarrollar. Como se controlará el número de personal en cada turno, definimos Xj como la cantidad de personal que entra a trabajar en el turno j, en donde varía j=1, . . . , 6. Es decir, hay una variable para cada turno.

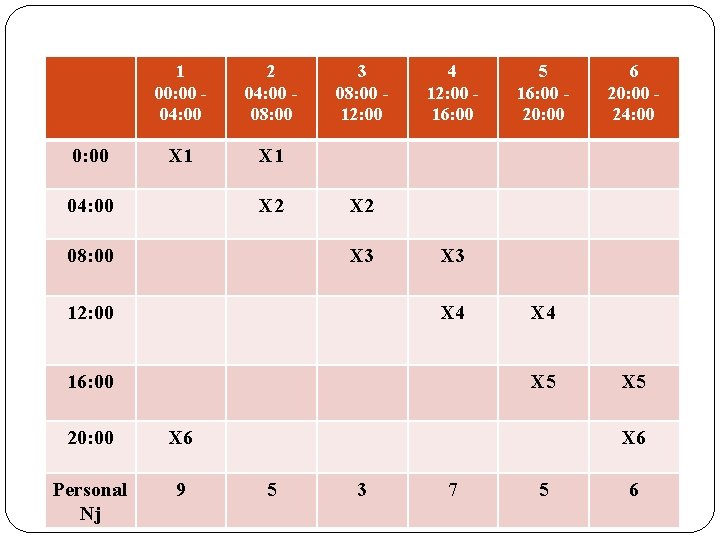
Las restricciones del modelo tienen que reflejar la necesidad de que la cantidad de personal que entren en el periodo j más el número de personas que entraron a trabajar en el turno j-1 sean suficientes para cubrir las necesidades del turno j (Nj). Esta situación queda reflejada en el Cuadro 2. En esta tabla, un trabajador que entra a trabajar, por ejemplo, a las 4: 00, trabajará en los turnos 2 y 3, y por tanto, contribuirá a cubrir las necesidades de estos dos turnos. En otras palabras, el turno j estará siendo atendido por Xj 1 y Xj. En consecuencia, tendremos que Xj-1 + Xj (el personal que trabaja durante el turno j) tiene que ser, como mínimo, igual a Nj, que es el número mínimo de personal de la farmacia que sería necesario para este turno. En términos matemáticos la restricción es la siguiente: Xj-1 + Xj ≥ Nj

El objetivo de la gerencia consiste en la minimización del número total de personal de atención necesario para cubrir las necesidades diarias. Este número será igual a X 1 +X 2 +X 3 +X 4 +X 5 +X 6 que representa la suma del número de personal que entra en cada periodo. Finalmente, el modelo matemático es el siguiente: 6 min Z = ∑ Xj j=1 Con las restricciones: X 6 + X 1 ≥ 9 Xj > 0, j= 1, . . . , 6 X 1 + X 2 ≥ 5 X 2 + X 3 ≥ 3 X 3 + X 4 ≥ 7 X 4 + X 5 ≥ 5 X 5 + X 6 ≥ 6

0: 00 1 00: 00 - 04: 00 2 04: 00 - 08: 00 X 1 04: 00 X 2 08: 00 3 08: 00 - 12: 00 4 12: 00 - 16: 00 5 16: 00 - 20: 00 X 2 X 3 12: 00 X 3 X 4 16: 00 X 4 X 5 20: 00 X 6 Personal Nj 9 6 20: 00 - 24: 00 X 5 X 6 5 3 7 5 6

Financiera El Banco BISA SA está preparando su plan de inversiones para los próximos dos años. Actualmente, la empresa tiene 1, 5 millones de dólares para invertir y espera ingresar, gracias a inversiones pasadas, un flujo de dinero al final de los meses, 6 12 y 18 próximos. Por otra parte, la empresa quiere expandirse y tiene dos propuestas sobre la mesa. La primera es asociarse con la empresa Minera San Cristobal y la segunda con la empresa Gravetal SA

En el Cuadro se muestra el flujo de caja (MILES DE DOLARES)del Banco BISA SA si entrara con un 100% en cada uno de INICIAL los proyectos. 6 MESES INVERSION ES PASADAS 12 MESES 18 MESES 24 MESES 500 400 380 MINERA SAN CRISTOBAL - 1000 - 700 1800 400 600 GRAVETAL S. A. - 800 500 -200 - 700 2000

Debido a regulaciones, al Banco BISA SA no se le permite pedir préstamos directos. Pero si que puede, cada seis meses, invertir sus fondos excedentes (es decir, aquellos que no ha invertido en ningún proyecto) en un fondo que le daría un 7% cada seis meses. Por otro lado, BISA SA puede participar en cada uno de los proyectos con un nivel inferior al 100% y, consecuentemente, el flujo de caja se reducirá en la misma proporción. Es decir, que si decide entrar por ejemplo con el 50% en el proyecto de Gravetal, el flujo correspondiente también se reducirá en la misma proporción. El problema que se plantea BISA SA es cuanto invertir en cada proyecto para maximizar el dinero en efectivo que tendrá la empresa en dos años

Formulación del problema Una vez el problema ha sido identificado y los parámetros del modelo han sido definidos, se tienen que definir las variables. Sea X 1 el porcentaje de participación en el proyecto Minera San Cristobal y X 2 el porcentaje de participación en el proyecto Gravetal SA (0 ≤ X 1 ≤ 1, 0 ≤ X 2 ≤ 1). Por otro lado, sean S 0, S 6, S 12 y S 18 el dinero que se depositará en el fondo en los periodos 0, 6 12 y 18 respectivamente.

Para formular las restricciones del modelo se utilizará un razonamiento secuencial. La empresa dispone de 1, 5 millones de dólares hoy (periodo 0) y las quiere gastar considerando las opciones siguientes: 1. participar en el proyecto Minera San Cristobal, que implicaría desembolsar 1. 000 X 1 dólares en el periodo 0; 2. participar en el proyecto Gravetal SA, teniendo que gastar 800. 000 X 2; 3. depositar el dinero al 7% Estas opciones no son excluyentes entre ellas. Por lo tanto, se tiene que cumplir la siguiente ecuación de equilibrio: 1. 500 = 1. 000 X 1 + 800 X 2 + S 0

Al cabo de seis meses, la empresa ingresará 500. 000 dólares, gracias a inversiones realizadas anteriormente. También el dinero depositado en el fondo en el periodo anterior estará a disposición junto con los intereses: S 0 + 0, 07 S 0. Por otra parte, el proyecto Gravetal SA dará una entrada de dinero igual a 500. 000 X 2. Con este dinero tendrá que hacer frente al compromiso adquirido con Minera San Cristobal, 700. 000 X 1, y depositar lo quede al 7% una vez más. Matemáticamente: 500 + 500 X 2 + 1, 07 S 0 = 700 X 1 + S 6

En el periodo 12, la empresa recibirá 400. 000 dólares, de inversiones anteriores, y 1. 800000 X 1 del proyecto Minera San Cristobal y el dinero del fondo junto con los intereses. Con estos ingresos tendrá que cubrir el compromiso del proyecto Gravetal SA, 200 X 2 y depositar S 12 en el fondo. En términos matemáticos: 400 + 1. 800 X 1 + 1, 07 S 6 = 200 X 2 + S 12

En el periodo 18, los ingresos que tendrá la empresa vendrán de inversiones anteriores (380. 000), del proyecto Minera San Cristobal (400. 000 X 1) y del depósito realizado en el periodo anterior incluyendo los intereses (1, 07 S 12 ). Con este dinero tendrá que realizar un gasto de 700. 000 X 2 en el proyecto Gravetal y el resto puede volver a ponerlo en el fondo (S 18). Es decir: 380 + 400 X 1 + 1, 07 S 12 = 700 X 2 + S 18

Finalmente, al cabo de dos años (periodo 24), el BISA tendrá únicamente ingresos y no tendrá ningún gasto. Los ingresos provienen de los dos proyectos (600. 000 X 1 + 2. 000 X 2) y del dinero depositado en el periodo anterior, 1, 07 S 18. Si se define Z como los ingresos realizados en el periodo 24 en miles de dólares, tendremos que: Z = 600 X 1 + 2. 000 X 2 + 1, 07 S 18 Este es el objetivo del problema: Maximizar los ingresos al cabo de dos años.

Finalmente, como solo se puede invertir un máximo de 100% en cada proyecto, las variables X 1 y X 2 no pueden exceder la unidad. Por lo tanto, hay que añadir las restricciones siguientes: X 1 ≤ 1 X 2 ≤ 1 El programa lineal se escribe de la forma siguiente: Max Z = 600 X 1 + 2. 000 X 2 + 1, 07 S 18 Con restricciones: 1000 X 1 + 800 X 2 + S 0 = 1. 500 700 X 1 -500 X 2 -1, 07 S 0 + S 6 = 500 -1. 800 X 1 + 200 X 2 -1, 07 S 6 + S 12 = 400 -400 X 1 + 700 X 2 -1, 07 S 12 + S 18 = 380 X 1 ≤ 1 ; X 2 ≤ 1 ; X 1, X 2, S 0, S 6, S 12, S 18 ≥ 0

Métodos de Resolución Un modelo matemático de decisión, por muy bien formulado que esté, no sirve de nada sino podemos encontrar una solución satisfactoria. Una de las características de la programación lineal es que, gracias a sus propiedades matemáticas, se consigue la solución óptima sin muchas dificultades. En primer lugar se verá el método gráfico, un sistema limitado a problemas con dos variables, y a continuación el método Simplex, el algoritmo más común para solucionar problemas lineales con muchas variables y restricciones.

Un modelo matemático de decisión, por muy bien formulado que esté, no sirve de nada sino podemos encontrar una solución satisfactoria. Una de las características de la programación lineal es que, gracias a sus propiedades matemáticas, se consigue la solución óptima sin muchas dificultades. En primer lugar se verá el método gráfico, un sistema limitado a problemas con dos variables, y a continuación el método Simplex, el algoritmo más común para solucionar problemas lineales con muchas variables y restricciones.

Anatina Toys fabrica 2 tipos de juguetes de madera, autitos y rompecabezas. Un autito se vende en Bs. 54 y requiere 20 Bs. de materia prima. Cada autito que se fabrica incrementa la mano de obra variable y los costos globales en 28 Bs. Un rompecabezas se vende en Bs. 42 y requiere 18 Bs. de materia prima. Cada rompecabezas incrementa la mano de obra variable y costos globales en 20 Bs. Para la fabricación se requiere mano de obra especializada: carpintera y acabados. Un autito requiere 2 h de acabado y 1 h de carpinteria. Un rompecabezas requiere 1 h acabado y 1 h de carpinteria.

Todas las semanas Anatina Toys consigue todo el material , pero solo 100 h de trabajo de acabado y 80 h de trabajo de carpinteria. La demanda de rompecabezas es ilimitada y solo se vende 40 autitos por semana. Anatina Toys debe maximizar las utilidades semanales (ingresos – costos) Diseñar un modelo matemático y resolver por el metodo grafico. X 1 = cantidad de autitos fabricados cada semana X 2 = cantidad de rompecabezas fabricados a la semana

La función objetivo será: Los ingresos semanales menos los costos de materia prima y menos los costos varables. Ingresos por semana = 54 X 1 + 42 X 2 Costos materia prima semana = 20 X 1 + 18 X 2 Costos variables semana = 28 X 1 + 20 X 2 Entonces Anatina Toys quiere maximizar: (54 X 1 + 42 X 2)-(20 X 1 + 18 X 2)-(28 X 1 + 20 X 2) = Max Z = 6 X 1 + 4 X 2 Los coeficientes para X 1 es 6 y para X 2 es 4 que es la utilidad.

RESTRICCIONES Restricción 1: 100 h de trabajo de acabado 2 X 1 + X 2 ≤ 100 Restricción 2: 80 h de trabajo de carpintería X 1 + X 2 ≤ 80 Restricción 3: Debido a la demanda limitada de autitos no debe producirse mas de 40 autitos. X 1 ≤ 40 Restricción 4 De signo: La producción no puede ser negativa. Entonces: X 1 ≥ 0 ; X 2 ≥ 0

REGION FACTIBLE Es el conjunto de todas las soluciones que satisfacen las restricciones. Por ej. Para X 1 = 40 y X 2 = 20 Cumple Para X 1 = 15 y X 2 =70 No Cumple Para X 1 = 10 y X 2 = 70 Cumple Para X 1 = 20 y X 2 = 60 Cumple SOLUCION OPTIMA: En Maximización es el punto donde el valor es el mas alto en la función objetivo En minimización es lo contrario. En nuestro caso el máximo es en Max Z = 6 X 1 + 4 X 2 Para X 1 = 20 y para X 2 = 60 Max Z = 360