Modelli di secondo grado Forma dellequazione Unequazione di

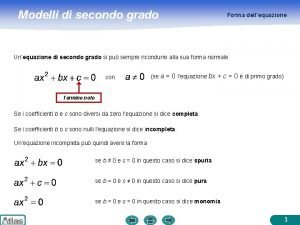
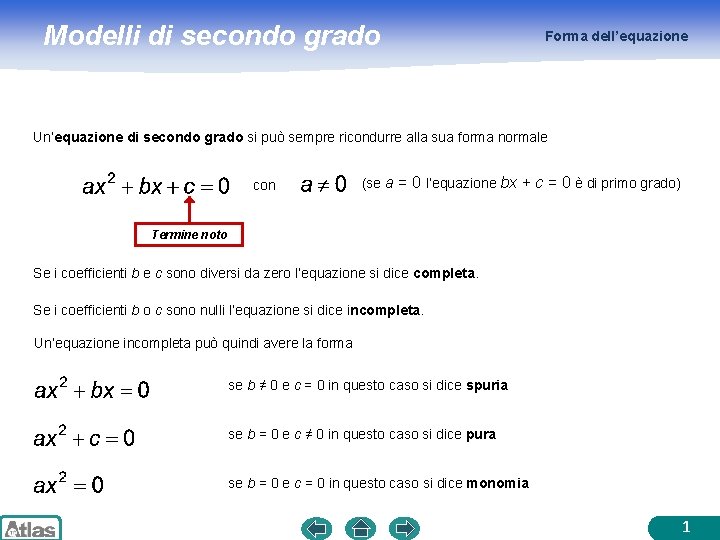
Modelli di secondo grado Forma dell’equazione Un’equazione di secondo grado si può sempre ricondurre alla sua forma normale con (se a = 0 l’equazione bx + c = 0 è di primo grado) Termine noto Se i coefficienti b e c sono diversi da zero l’equazione si dice completa. Se i coefficienti b o c sono nulli l’equazione si dice incompleta. Un’equazione incompleta può quindi avere la forma se b ≠ 0 e c = 0 in questo caso si dice spuria se b = 0 e c ≠ 0 in questo caso si dice pura se b = 0 e c = 0 in questo caso si dice monomia 1

Modelli di secondo grado Forma dell’equazione ESEMPIO È completa l’equazione dove è a = 4, b = − 3, c = 1 È incompleta spuria l’equazione dove è a = 3, b = − 5, c = 0 È incompleta pura l’equazione dove è a = 1, b = 0, c = − 6 È monomia l’equazione dove è a = 7, b = 0, c = 0 2

Modelli di secondo grado Risoluzione di equazioni incomplete Regole generali per la risoluzione delle equazioni di secondo grado incomplete. § Equazione della forma Si raccoglie x a fattore comune: Si applica la legge di annullamento del prodotto: L’equazione spuria ammette sempre due soluzioni di cui una è zero. ESEMPIO 3

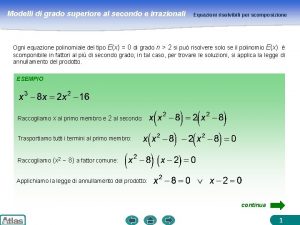
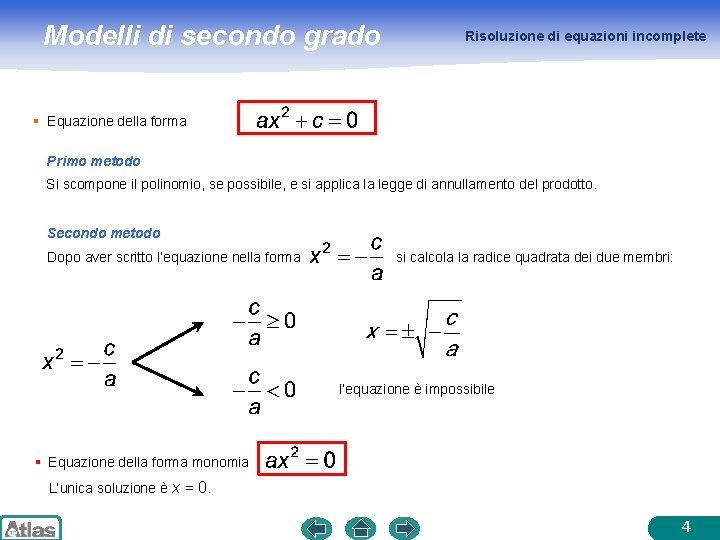
Modelli di secondo grado Risoluzione di equazioni incomplete § Equazione della forma Primo metodo Si scompone il polinomio, se possibile, e si applica la legge di annullamento del prodotto. Secondo metodo Dopo aver scritto l’equazione nella forma si calcola la radice quadrata dei due membri: l’equazione è impossibile § Equazione della forma monomia L’unica soluzione è x = 0. 4

Modelli di secondo grado Risoluzione di equazioni incomplete ESEMPI Primo metodo Secondo metodo La somma di due quadrati non è scomponibile e non si annulla mai. Equazione impossibile 5

Modelli di secondo grado Formula risolutiva L’equazione di secondo grado ax 2 + bx + c = 0, nell’ipotesi che sia a ≠ 0 ∧ b 2 − 4 ac ≥ 0, ammette come soluzioni i numeri reali dati dalle seguenti espressioni ∨ L’espressione Δ = b 2 − 4 ac è il discriminante dell’equazione e si verifica che: • se Δ > 0 l’equazione ammette come soluzioni due numeri reali diversi (si dice che le soluzioni sono reali distinte) • se Δ = 0 l’equazione ammette come soluzione due numeri reali uguali (si dice che le soluzioni sono reali coincidenti) • se Δ < 0 l’equazione non ammette soluzioni reali. 6

Modelli di secondo grado Risoluzione equazioni complete ESEMPI 1. Risolviamo l’equazione nella quale a = 2; b = 1; c = − 6 7

Modelli di secondo grado Risoluzione equazioni complete ESEMPI 2. Risolviamo l’equazione nella quale a = 1; b = 8; c = 16 3. Risolviamo l’equazione nella quale a = 1; b = − 3; c = 8 8

Modelli di secondo grado Formula risolutiva Se il coefficiente b dell’equazione ax 2 + bx + c = 0 è un numero pari, si può utilizzare la formula ridotta: ESEMPIO 9

Modelli di secondo grado Equazioni frazionarie Nel caso di equazione frazionaria seguiamo la seguente procedura: • determinazione del dominio D; • riduzione dell’equazione alla forma intera; • applicazione della formula risolutiva se è completa o degli algoritmi specifici se è incompleta; • controllo dell’accettabilità delle soluzioni confrontandole con il dominio. ESEMPIO Il dominio dell’equazione è D = R − {0} Scriviamo l’equazione in forma normale Applichiamo la formula ridotta: 10

Modelli di secondo grado Equazioni letterali Quando un’equazione contiene dei parametri è necessario discutere che cosa accade all’insieme delle soluzioni al variare di tali parametri. Procedura risolutiva generale da seguire § Bisogna stabilire qual è il dominio dell’equazione, cioè l’insieme dei valori che può assumere l’incognita: il dominio è in genere R se l’equazione è intera, è R esclusi i valori che rendono nulli i denominatori se l’equazione è frazionaria. Per esempio: ha dominio R poiché deve essere x ≠ 2 e x ≠ a, ha dominio R − {2, a} 11

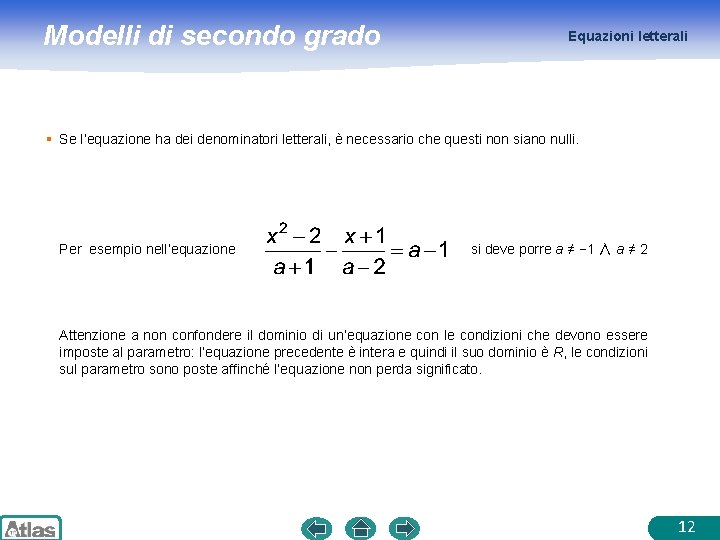
Modelli di secondo grado Equazioni letterali § Se l’equazione ha dei denominatori letterali, è necessario che questi non siano nulli. Per esempio nell’equazione si deve porre a ≠ − 1 ∧ a ≠ 2 Attenzione a non confondere il dominio di un’equazione con le condizioni che devono essere imposte al parametro: l’equazione precedente è intera e quindi il suo dominio è R, le condizioni sul parametro sono poste affinché l’equazione non perda significato. 12

Modelli di secondo grado Equazioni letterali § Si devono applicare correttamente i principi di equivalenza delle equazioni; per esempio si deve essere certi che, quando si dividono entrambi i membri di un’equazione per una stessa espressione letterale, questa non sia nulla: si può dividere per 3 si può dividere per a solo se a ≠ 0 § Quando si applica la formula risolutiva, si deve essere certi che il coefficiente a di x 2 non sia nullo perché, in caso contrario, la formula non si può applicare. Si può applicare la formula (ridotta) Si può applicare la formula solo se a ≠ 1 13

Modelli di secondo grado Equazioni letterali L’insieme dei ragionamenti che si fanno sul parametro per stabilire quante e quali sono le soluzioni di un’equazione rappresenta la discussione dell’equazione. Uno schema generale su come procedere è il seguente. § Caso dell’equazione intera Il dominio è R, non ci sono condizioni sull’incognita; possono però esserci condizioni iniziali sul parametro. Arrivati alla forma normale: § si pone il coefficiente di x 2 diverso da zero (questa operazione non è necessaria se tale coefficiente è numerico o se la condizione coincide con una di quelle iniziali) e si risolve l’equazione; § si verifica che cosa accade quando il parametro assume quel o quei valori che sono stati esclusi al punto precedente. Inoltre, quando il discriminante è letterale e non è un quadrato perfetto, l’equazione ammette soluzioni reali solo se vale la condizione Δ ≥ 0. Esempio: e deve essere 1 − a ≥ 0 14

Modelli di secondo grado Equazioni letterali ESEMPIO Riscriviamo l’equazione in forma normale: L’equazione è incompleta e per risolverla ricaviamo l’espressione di x 2: • se b ≠ 3 Le soluzioni sono reali se b − 3 > 0, cioè b > 3 • se b = 3 l’equazione diventa: che è impossibile 15

Modelli di secondo grado Equazioni letterali § Caso dell’equazione frazionaria Il dominio è R, ad esclusione dei valori dell’incognita che annullano i denominatori; possono anche esserci condizioni iniziali sul parametro. Arrivati alla forma normale: § si pone il coefficiente di x 2 diverso da zero (questa operazione non è necessaria se tale coefficiente è numerico o se la condizione coincide con una di quelle iniziali) e si risolve l’equazione; trovate le soluzioni si procede al confronto con le condizioni imposte dal dominio; § si verifica che cosa accade quando il parametro assume quel o quei valori che sono stati esclusi al punto precedente. 16

Modelli di secondo grado Equazioni letterali ESEMPIO L’equazione è frazionaria e deve essere x ≠ 0 quindi D = R − {0} Scriviamola in forma normale: Calcoliamo il discriminante: Il coefficiente di x 2 è numerico, troviamo subito le soluzioni: continua 17

Modelli di secondo grado Equazioni letterali Vediamo se le soluzioni trovate sono accettabili: • la soluzione − 2 appartiene sicuramente al dominio; • dobbiamo invece confrontare la soluzione Quindi se b = 0 la soluzione Riassumendo: con 0: se non è accettabile e deve essere scartata. se b ≠ 0 se b = 0 18

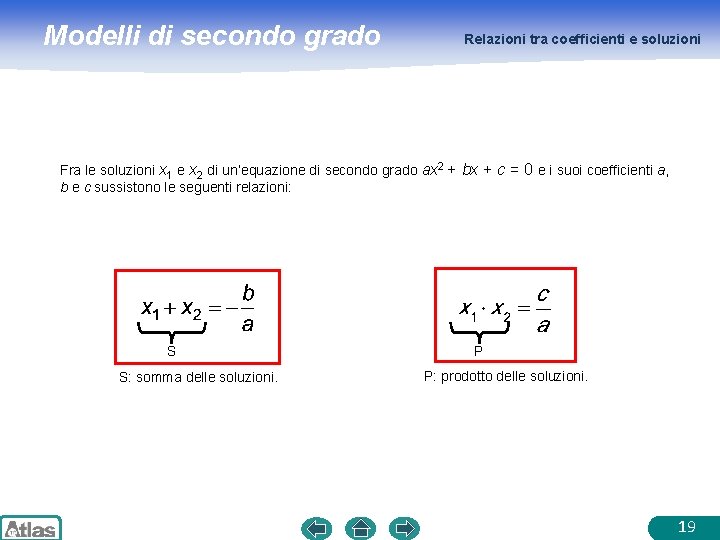
Modelli di secondo grado Relazioni tra coefficienti e soluzioni Fra le soluzioni x 1 e x 2 di un’equazione di secondo grado ax 2 + bx + c = 0 e i suoi coefficienti a, b e c sussistono le seguenti relazioni: S S: somma delle soluzioni. P P: prodotto delle soluzioni. 19

Modelli di secondo grado Relazioni tra coefficienti e soluzioni Mediante l’utilizzo di tali relazioni è possibile risolvere i seguenti problemi: 1. Trovare le soluzioni di un’equazione senza applicare la formula risolutiva. Per trovare le soluzioni dell’equazione x 2 − 4 x − 5 = 0 senza utilizzare la formula risolutiva basta calcolare: Dobbiamo trovare due numeri la cui somma è 4 e il cui prodotto è − 5: x 1 = − 1 e x 2 = 5 infatti − 1 + 5 = 4 e − 1 5 = − 5 20

Modelli di secondo grado 2. Relazioni tra coefficienti e soluzioni Individuare due numeri conoscendo la loro somma e il loro prodotto. Per determinare due numeri di cui si conoscono somma s e prodotto p basta risolvere l’equazione x 2 − sx + p = 0 Le sue soluzioni sono i numeri richiesti. Se e I due numeri sono e 21

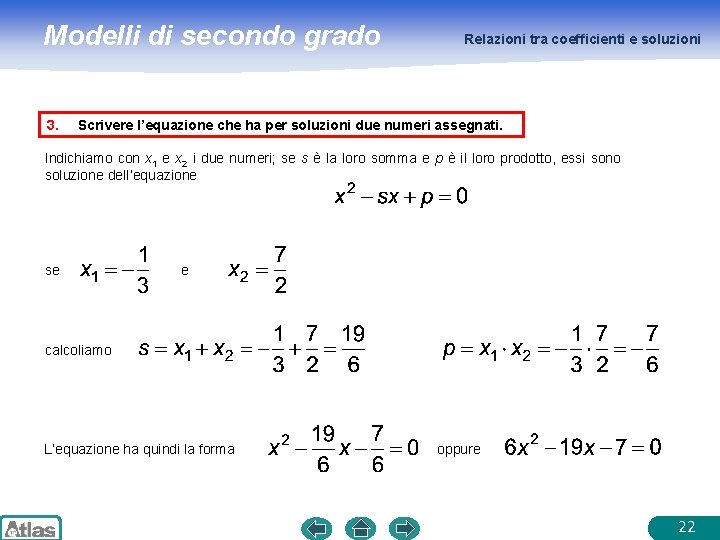
Modelli di secondo grado 3. Relazioni tra coefficienti e soluzioni Scrivere l’equazione che ha per soluzioni due numeri assegnati. Indichiamo con x 1 e x 2 i due numeri; se s è la loro somma e p è il loro prodotto, essi sono soluzione dell’equazione se e calcoliamo L’equazione ha quindi la forma oppure 22

Modelli di secondo grado Relazioni tra coefficienti e soluzioni Scomposizione del trinomio di secondo grado Se ax 2 + bx + c è un trinomio di secondo grado con a ≠ 0 e se x 1 e x 2 sono le eventuali radici (cioè le soluzioni reali dell’equazione associata ax 2 + bx + c = 0), si ha che: • se Δ > 0 ax 2 + bx + c = a (x − x 1)(x − x 2) • se Δ = 0 ax 2 + bx + c = a (x − x 1)2 • se Δ < 0 ax 2 + bx + c è irriducibile ESEMPIO Scomponiamo: Risolviamo l’equazione associata: Si ha quindi che: 23

Modelli di secondo grado La funzione Rappresentazione di una parabola rappresenta una parabola con vertice Per determinare l’ordinata del vertice, una volta trovata l’ascissa, si può sostituire l’ascissa trovata al posto della x nell’equazione della parabola. Per disegnare una parabola, oltre al vertice si cercano alcuni punti del grafico. ESEMPIO L’ascissa del vertice è Per l’ordinata sostituiamo l’ascissa nell’equazione Il vertice ha coordinate Troviamo ora alcuni punti del grafico: (0, − 5), (1, − 8) e (5, 0). 24

Modelli di secondo grado Rappresentazione di una parabola Gli zeri di una parabola sono le ascisse dei punti di intersezione tra la parabola e l’asse delle ascisse. Quindi sono le soluzioni dell’equazione associata alla parabola. ESEMPIO Per determinare gli zeri della parabola Bisogna risolvere l’equazione Quindi gli zeri sono x = 5 e x = − 1 e rappresentano i punti in cui la parabola interseca l’asse delle x. 25

Modelli di secondo grado Disequazioni di secondo grado Per risolvere la disequazione ax 2 + bx + c > 0 oppure ax 2 + bx + c < 0 con a > 0: § consideriamo la parabola y = ax 2 + bx + c associata al trinomio al primo membro § troviamo le sue intersezioni con l’asse x risolvendo l’equazione ax 2 + bx + c = 0; si possono presentare i seguenti casi a seconda del valore del discriminante: • Δ > 0: ci sono due intersezioni x 1 e x 2 con l’asse x ed il trinomio è • positivo per x < x 1 o x > x 2 • negativo per x 1 < x 2 • Δ = 0: c’è una sola intersezione x 1 con l’asse delle x ed il trinomio è: • sempre positivo tranne per x = x 1 dove si annulla • Δ < 0: non ci sono intersezioni con l’asse x ed il trinomio è: • sempre positivo § scegliamo l’intervallo delle soluzioni a seconda del verso della disequazione: • nella disequazione ax 2 + bx + c > 0 ricerchiamo gli intervalli di positività • nella disequazione ax 2 + bx + c < 0 ricerchiamo gli intervalli di negatività. 26

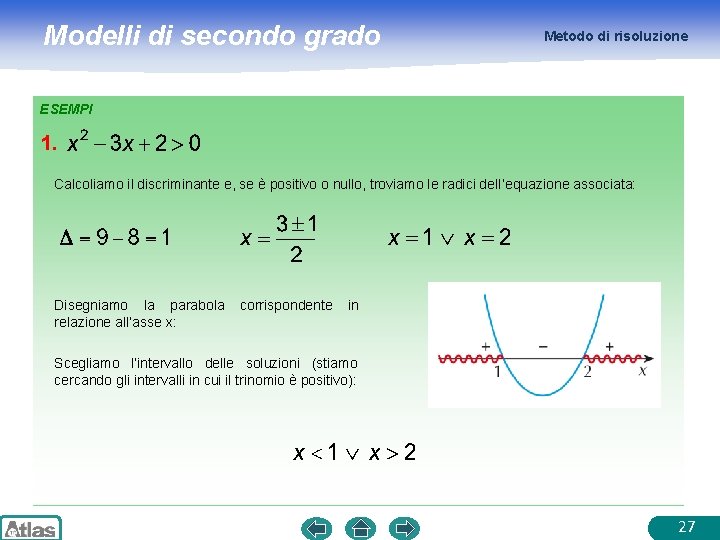
Modelli di secondo grado Metodo di risoluzione ESEMPI 1. Calcoliamo il discriminante e, se è positivo o nullo, troviamo le radici dell’equazione associata: Disegniamo la parabola relazione all’asse x: corrispondente in Scegliamo l’intervallo delle soluzioni (stiamo cercando gli intervalli in cui il trinomio è positivo): 27

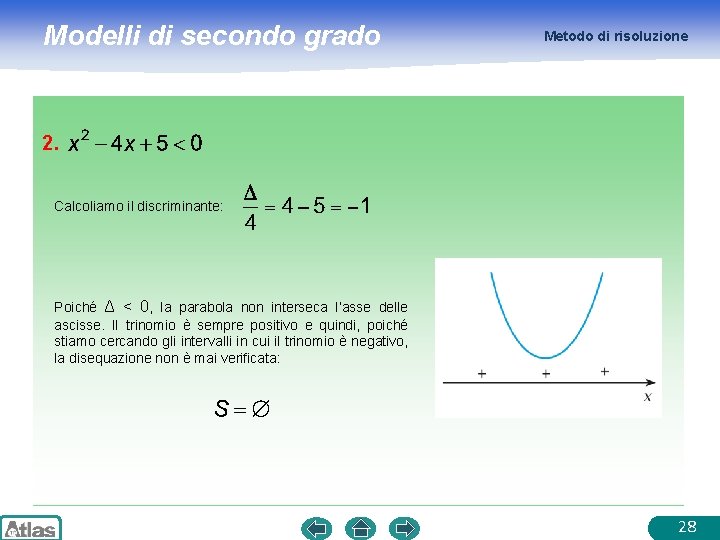
Modelli di secondo grado Metodo di risoluzione 2. Calcoliamo il discriminante: Poiché Δ < 0, la parabola non interseca l’asse delle ascisse. II trinomio è sempre positivo e quindi, poiché stiamo cercando gli intervalli in cui il trinomio è negativo, la disequazione non è mai verificata: 28

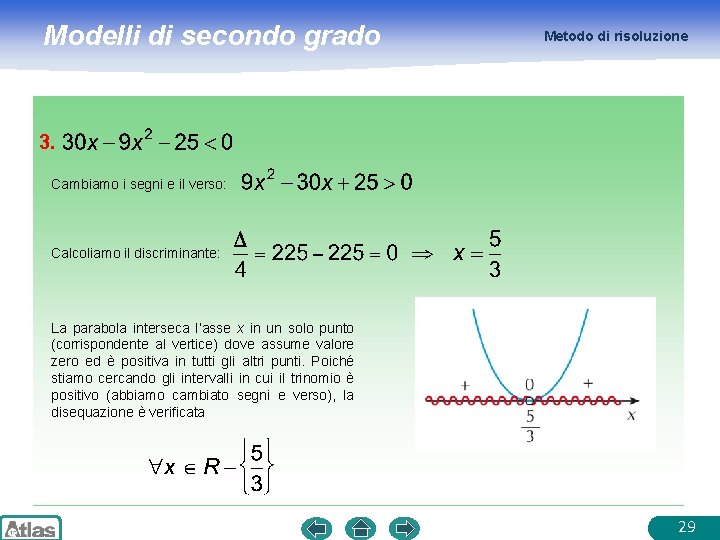
Modelli di secondo grado Metodo di risoluzione 3. Cambiamo i segni e il verso: Calcoliamo il discriminante: La parabola interseca l’asse x in un solo punto (corrispondente al vertice) dove assume valore zero ed è positiva in tutti gli altri punti. Poiché stiamo cercando gli intervalli in cui il trinomio è positivo (abbiamo cambiato segni e verso), la disequazione è verificata 29

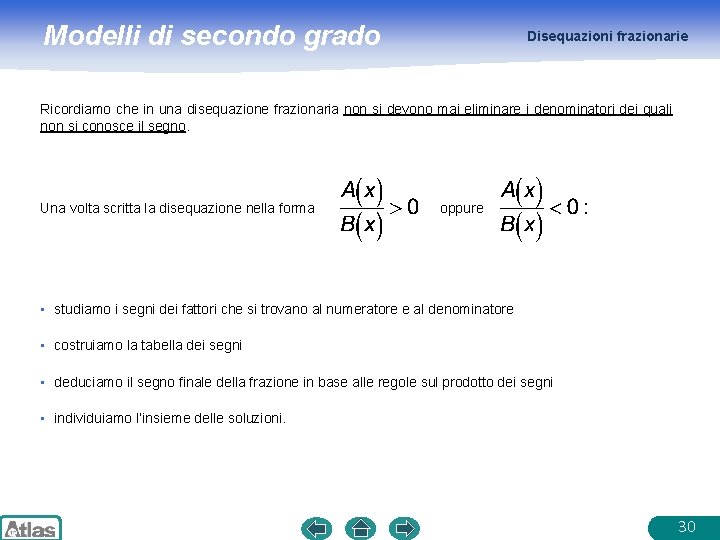
Modelli di secondo grado Disequazioni frazionarie Ricordiamo che in una disequazione frazionaria non si devono mai eliminare i denominatori dei quali non si conosce il segno. Una volta scritta la disequazione nella forma oppure • studiamo i segni dei fattori che si trovano al numeratore e al denominatore • costruiamo la tabella dei segni • deduciamo il segno finale della frazione in base alle regole sul prodotto dei segni • individuiamo l’insieme delle soluzioni. 30

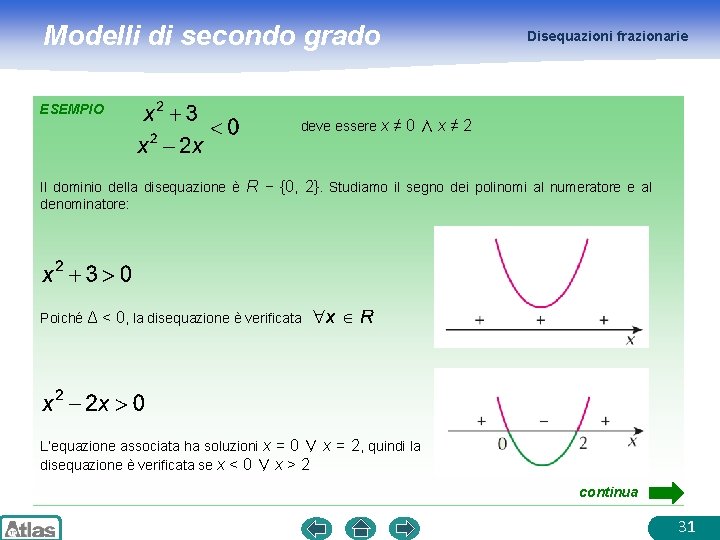
Modelli di secondo grado ESEMPIO Disequazioni frazionarie deve essere x ≠ 0 ∧ x ≠ 2 Il dominio della disequazione è R − {0, 2}. Studiamo il segno dei polinomi al numeratore e al denominatore: Poiché Δ < 0, la disequazione è verificata L’equazione associata ha soluzioni x = 0 ∨ x = 2, quindi la disequazione è verificata se x < 0 ∨ x > 2 continua 31

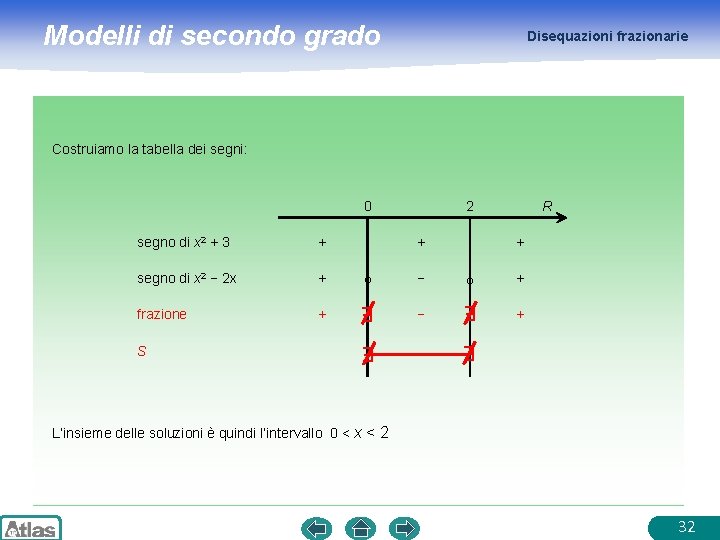
Modelli di secondo grado Disequazioni frazionarie Costruiamo la tabella dei segni: 0 2 R segno di x 2 + 3 + + + segno di x 2 − 2 x + − + frazione + E E E S − L’insieme delle soluzioni è quindi l’intervallo 0 < x < 2 32

Modelli di secondo grado Sistemi di disequazioni Un sistema di disequazioni è verificato nell’insieme intersezione delle soluzioni di ciascuna disequazione; conviene quindi: • risolvere ciascuna disequazione • costruire la tabella delle soluzioni in modo da mettere in evidenza le eventuali intersezioni. ESEMPIO Risolviamo la prima disequazione: S 1 Risolviamo la seconda disequazione: S 2 Tabella delle soluzioni: − 1 0 8 R S 1 S 2 Il sistema è verificato se 0 ≤ x ≤ 8 S 33

Modelli di secondo grado Equazioni e disequazioni con i moduli Un’equazione o una disequazione con i moduli si risolve distinguendo il caso in cui l’espressione nel modulo è positiva o nulla da quando è negativa. ESEMPIO Il primo sistema è impossibile mentre il secondo ha per soluzione Quindi 34

Modelli di secondo grado Sistemi non lineari Un sistema è non lineare se almeno una delle sue equazioni è di grado superiore al primo. In particolare: • in un sistema di secondo grado tutte le equazioni sono di primo grado tranne una che è di secondo; • in un sistema di terzo grado tutte le equazioni sono di primo grado tranne una che è di terzo; Per risolvere un sistema non lineare si applicano i principi di sostituzione e di riduzione. § Principio di sostituzione. Se in un sistema si sostituisce ad una incognita la sua espressione ricavata da un’altra equazione, si ottiene un sistema equivalente a quello dato. § Principio di riduzione. Se in un sistema si sommano membro a membro le sue equazioni (tutte o solo alcune) e si sostituisce l’equazione ottenuta ad una di esse, si ottiene un sistema equivalente a quello dato. 35

Modelli di secondo grado Sistemi non lineari ESEMPIO Il sistema è di secondo grado e rappresenta l’intersezione tra una parabola e una retta. Se nel sistema è presente un’equazione di primo grado, conviene ricavare l’espressione di una delle incognite da tale equazione e sostituire poi nell’altra. Risolvendo la prima equazione si ottiene x = 2 e x = -1 Quindi le soluzioni del sistema sono La parabola e la retta si intersecano nei punti A (2, 5) e B (-1, 2) 36