Regla Multiplicativa Ing Ral Alvarez Guale MPC Regla

Regla Multiplicativa Ing. Raúl Alvarez Guale, MPC

Regla de producto o regla multiplicativa Teorema: Si en un experimento pueden ocurrir los eventos A y B, entonces P(A ∩ B) = P(A)P(B|A), siempre que P(A) > 0. Como los eventos A ∩ B y B ∩ A son equivalentes P(A ∩ B) = P(B ∩ A) = P(B)P(A|B).

Ejemplo 1 Suponga que tenemos una caja de fusibles que contiene 20 unidades, de las cuales 5 están defectuosas. Si se seleccionan 2 fusibles al azar y se retiran de la caja, uno después del otro, sin reemplazar el primero, ¿cuál es la probabilidad de que ambos fusibles estén defectuosos?

Ejemplo 1 •

Ejemplo 1 •

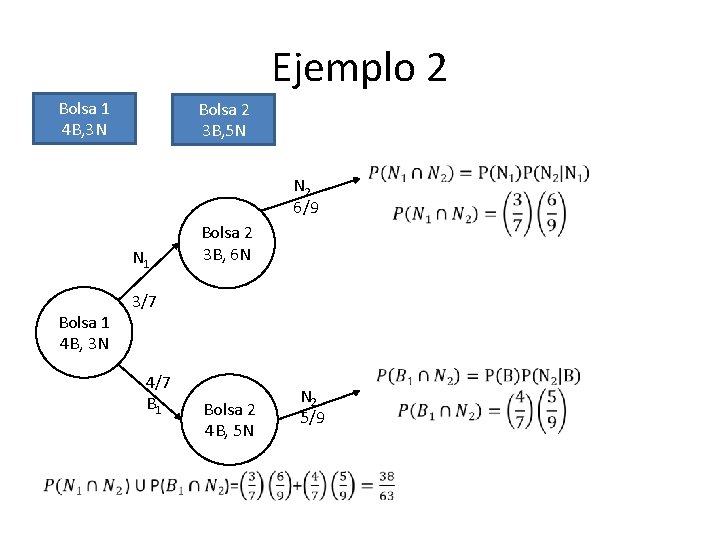
Ejemplo 2 Una bolsa contiene 4 bolas blancas y 3 negras, y una segunda bolsa contiene 3 blancas y 5 negras. Se saca una bola de la primera bolsa y se coloca sin verla en la segunda bolsa. ¿Cuál es la probabilidad de que ahora se saque una bola negra de la segunda bolsa?

Ejemplo 2 Solución: N 1 = Sale una bola negra bolsa 1 N 2 = Sale una bola negra bolsa 2 B 1 = Sale una bola blanca bolsa 1 “Se saca una y se pone en otra sin ver el color” ¿Cuál es la probabilidad de que ahora se saque una bola negra de la segunda bolsa?

Ejemplo 2 •

Ejemplo 2 Bolsa 1 4 B, 3 N Bolsa 2 3 B, 5 N N 2 6/9 N 1 Bolsa 1 4 B, 3 N Bolsa 2 3 B, 6 N 3/7 4/7 B 1 Bolsa 2 4 B, 5 N N 2 5/9

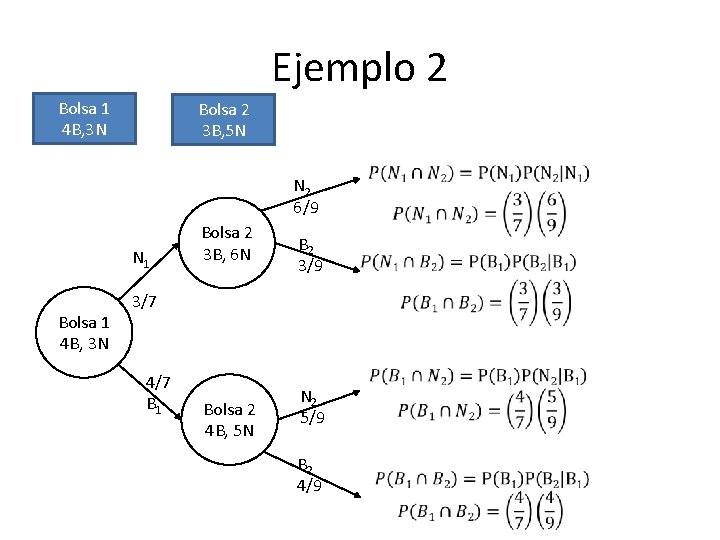
Ejemplo 2 Bolsa 1 4 B, 3 N Bolsa 2 3 B, 5 N N 2 6/9 N 1 Bolsa 1 4 B, 3 N Bolsa 2 3 B, 6 N B 2 3/9 3/7 4/7 B 1 Bolsa 2 4 B, 5 N N 2 5/9 B 2 4/9

Teorema Dos eventos A y B son independientes si y solo si P(A ∩ B) = P(A)P(B). Por lo tanto, para obtener la probabilidad de que ocurran dos eventos independientes simplemente calculamos el producto de sus probabilidades individuales.

Ejemplo 3 Una pequeña ciudad dispone de un carro de bomberos y una ambulancia para emergencias. La probabilidad de que el carro de bomberos esté disponible cuando se necesite es 0. 98 y la probabilidad de que la ambulancia esté disponible cuando se le requiera es 0. 92. En el evento de un herido en un incendio, calcule la probabilidad de que tanto la ambulancia como el carro de bomberos estén disponibles, suponiendo que operan de forma independiente.

Ejemplo 3 Solución: A = Carro bomberos disponibles P(A) = 0. 98 B = Ambulancia disponible P(B) = 0. 92 La probabilidad de que ambos vehículos estén disponibles es: P(A ∩ B)=P(A)P(B)=(0. 98)(0. 92)=0. 9016 Ya que son eventos independientes

Ejemplo 4 Un sistema eléctrico consta de cuatro componentes, como se ilustra en la figura. El sistema funciona si los componentes A y B funcionan, y si funciona cualquiera de los componentes C o D. La confiabilidad (probabilidad de que funcionen) de cada uno de los componentes también se muestra en la figura. Calcule la probabilidad de a) que el sistema completo funcione y de b) que el componente C no funcione, dado que el sistema completo funciona. Suponga que los cuatro componentes funcionan de manera independiente.

Ejemplo 4

Ejemplo 4 Solución: a) que el sistema completo funcione Evento X Evento Y

Ejemplo 4 •

Ejemplo 4 •

Teorema Si, en un experimento, pueden ocurrir los eventos A 1, A 2, . . . , Ak, entonces P(A 1∩A 2∩···∩Ak) = P(A 1)P(A 2|A 1)P(A 3|A 1∩A 2)…P(Ak|A 1∩A 2∩…∩Ak-1) Si los eventos A 1, A 2, . . . , Ak son independientes, entonces P(A 1 ∩ A 2 ∩···∩Ak) = P(A 1)P(A 2)…P(Ak)

Ejemplo 5 Se sacan tres cartas seguidas, sin reemplazo, de una baraja ordinaria. Encuentre la probabilidad de que ocurra el evento A 1 ∩ A 2 ∩ A 3, donde A 1 es el evento de que la primera carta sea un as rojo, A 2 el evento de que la segunda carta sea un 10 o una jota y A 3 el evento de que la tercera carta sea mayor que 3 pero menor que 7.

Ejemplo 5 •

Ejemplo 5 •

Definición Un conjunto de eventos a = {A 1, …, An} son mutuamente independientes si para cualquier subconjunto de a, Ai 1. . . , Aik, para k ≤ n, tenemos P(Ai 1 ∩···∩ Aik) = P(Ai 1)…P(Aik).

Gracias