La rgression simple Michel Tenenhaus 1 La rgression

La régression simple Michel Tenenhaus 1

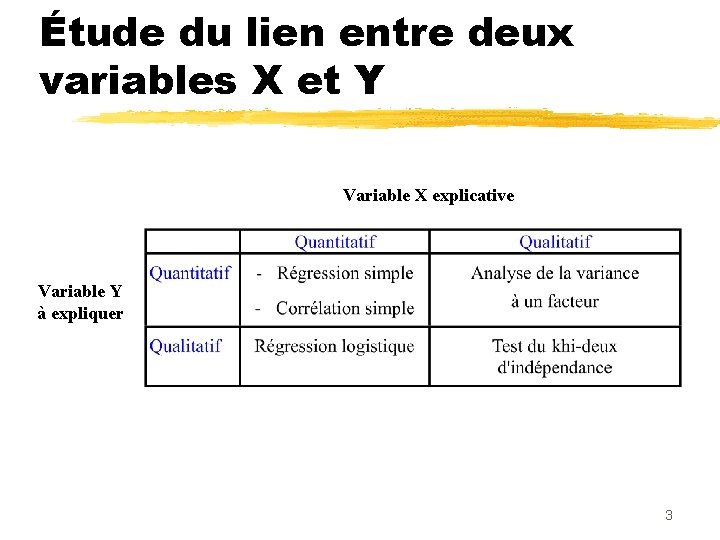
La régression simple Étude de la liaison linéaire entre deux variables numériques : - une variable explicative X - une variable à expliquer Y 2

Étude du lien entre deux variables X et Y Variable X explicative Variable Y à expliquer 3

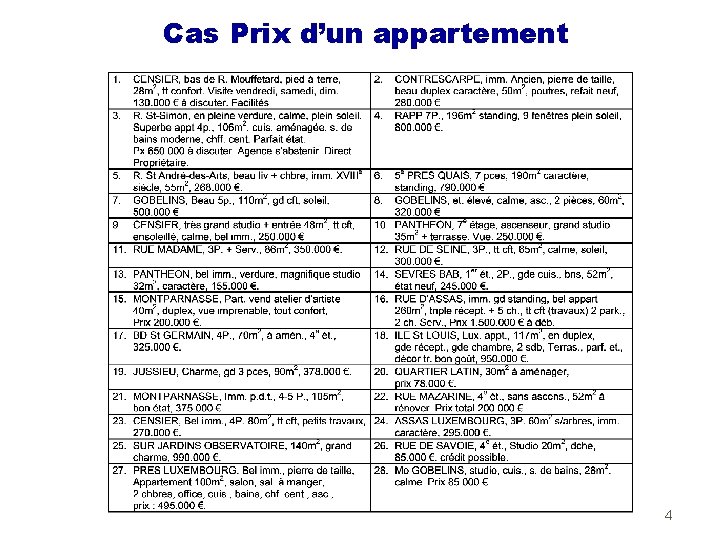
Cas Prix d’un appartement 4

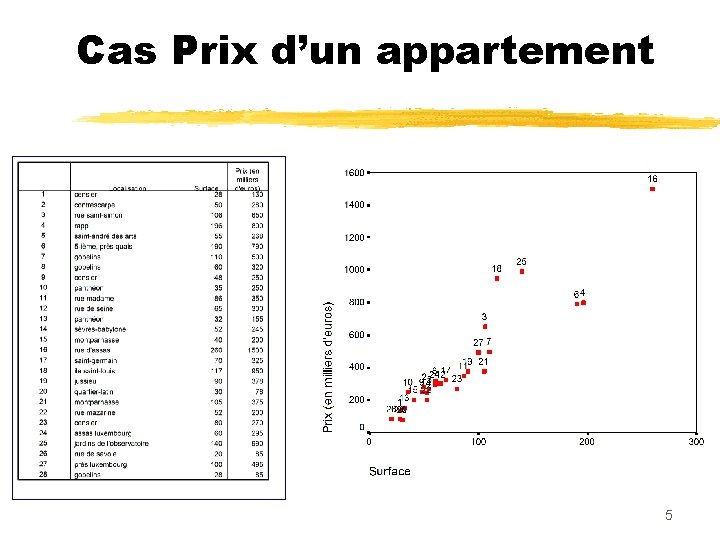
Cas Prix d’un appartement 5

Identification des outliers au niveau du Prix au mètre carré 9000 Ile saint-louis 8000 Panthéon (10) 7000 Jardins de l'observatoire 6000 5000 4000 3000 2000 N= 28 Prix du mètre carré 6

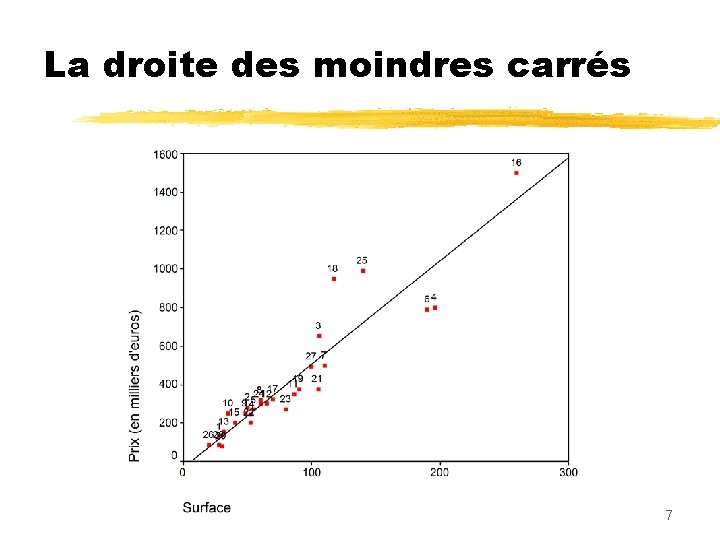
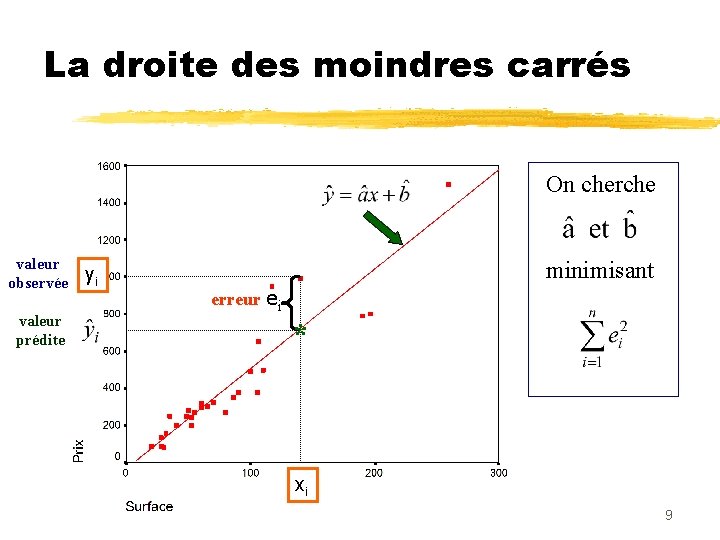
La droite des moindres carrés 7

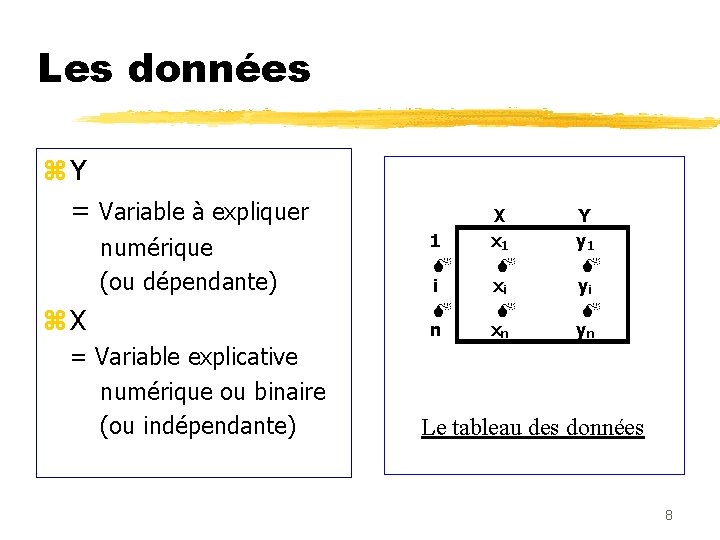
Les données z. Y = Variable à expliquer numérique (ou dépendante) z. X = Variable explicative numérique ou binaire (ou indépendante) 1 M i M n X x 1 M xi M xn Y y 1 M yi M yn Le tableau des données 8

La droite des moindres carrés On cherche valeur observée valeur prédite yi minimisant erreur ei * xi 9

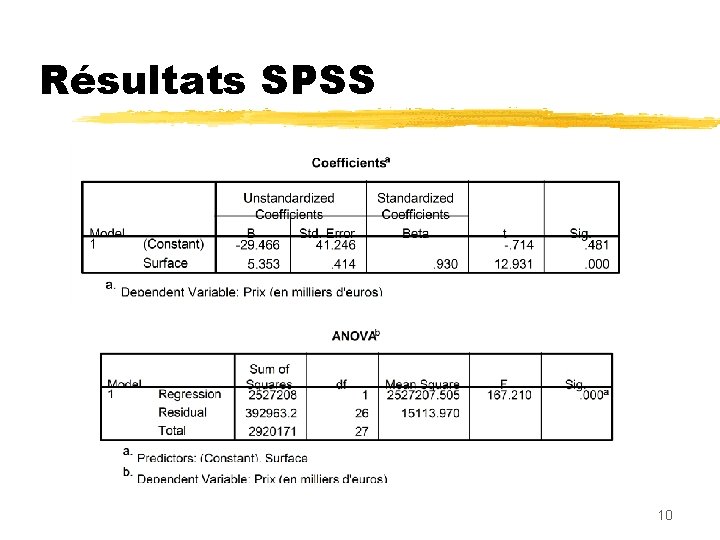
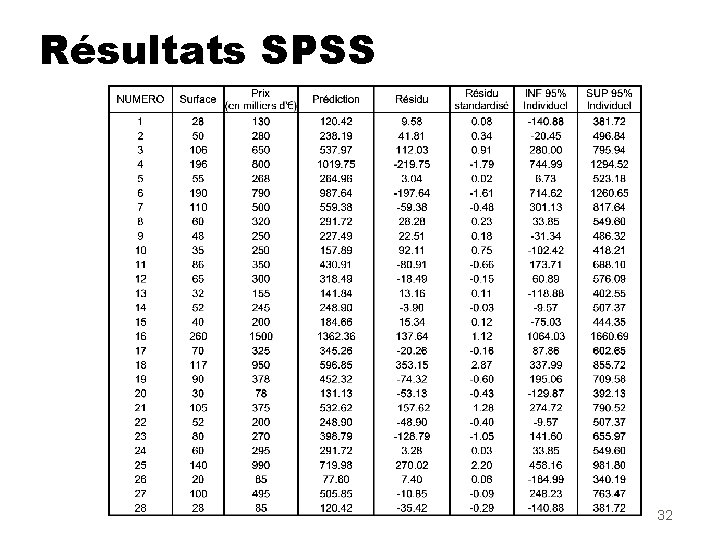
Résultats SPSS 10

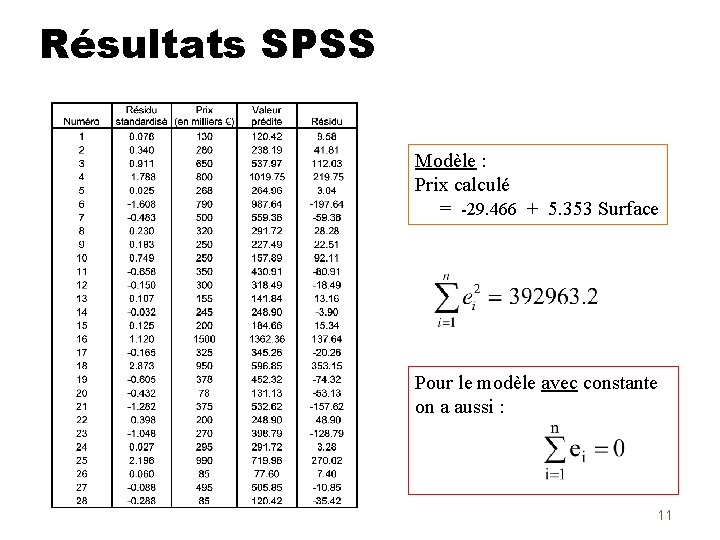
Résultats SPSS Modèle : Prix calculé = -29. 466 + 5. 353 Surface Pour le modèle avec constante on a aussi : 11

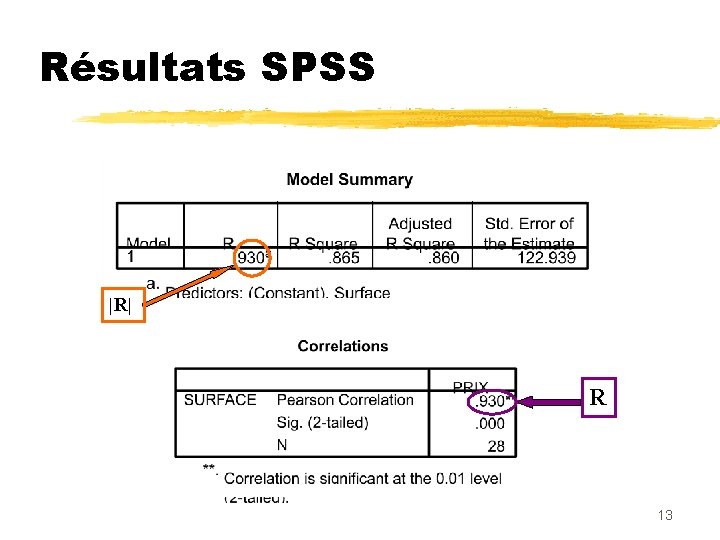
Coefficient de détermination R 2, Coefficient de corrélation R A) Formule de décomposition Somme des carrés totale Somme des carrés expliquée Somme des carrés résiduelle (Total Sum of Squares) (Regression Sum of Squares) (Residual Sum of Squares) B) R 2 = C) R = signe( ) 12

Résultats SPSS |R| R 13

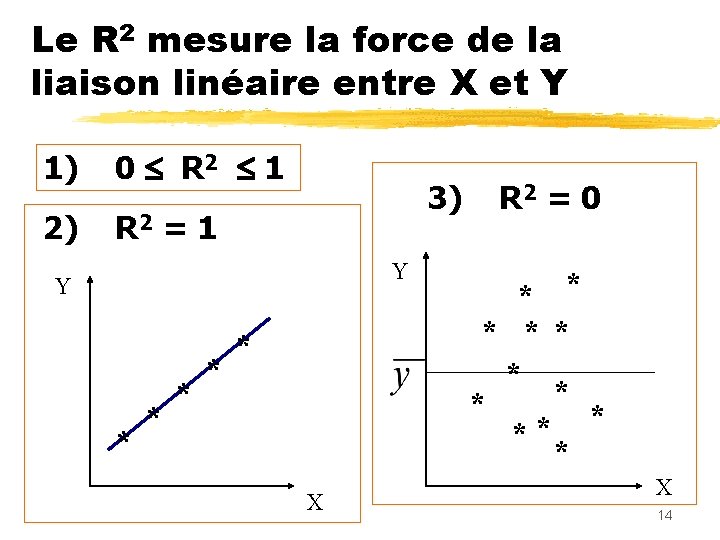
Le R 2 mesure la force de la liaison linéaire entre X et Y 1) 0 R 2 1 2) R 2 = 1 3) Y Y * * * X R 2 = 0 * * * X 14

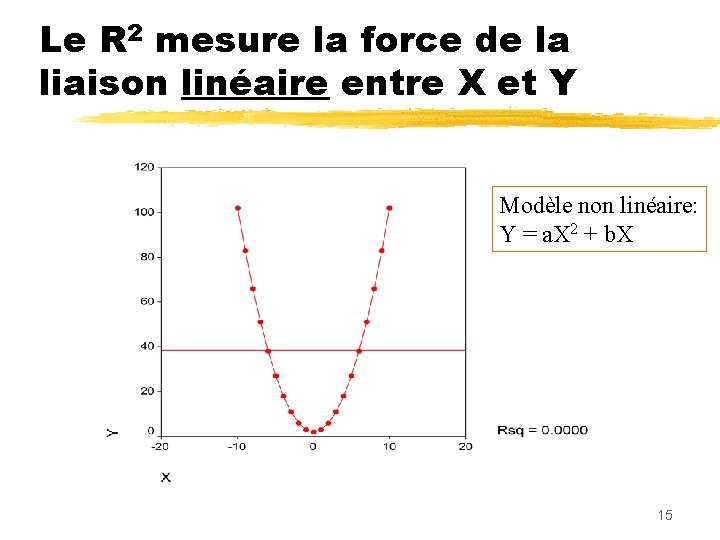
Le R 2 mesure la force de la liaison linéaire entre X et Y Modèle non linéaire: Y = a. X 2 + b. X 15

La corrélation R mesure la force et le sens de la liaison linéaire entre X et Y Y Y * * * * ** * X 16

Calcul direct de R Résultat SPSS : 17

La corrélation R est-elle significative au risque = 0. 05 ? z Notations - = Corrélation au niveau de la population z Règle de décision On rejette H 0 au risque = 0. 05 de se tromper si - R = Corrélation au niveau de l’échantillon z Test : H 0 : = 0 (Bonne approximation pour n > 20) H 1 : 0 18

La corrélation R est-elle significative au risque ? z Notations - = Corrélation au niveau de la population - R = Corrélation au niveau z Règle de décision On rejette H 0 au risque de se tromper si de l’échantillon z Test : H 0 : = 0 H 1 : 0 z Niveau de signification Plus petit conduisant au rejet de H 0. 19

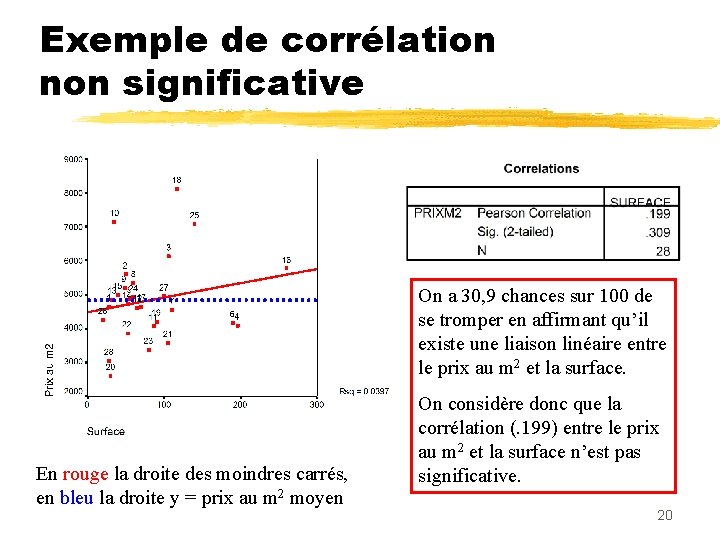
Exemple de corrélation non significative On a 30, 9 chances sur 100 de se tromper en affirmant qu’il existe une liaison linéaire entre le prix au m 2 et la surface. En rouge la droite des moindres carrés, en bleu la droite y = prix au m 2 moyen On considère donc que la corrélation (. 199) entre le prix au m 2 et la surface n’est pas significative. 20

Le modèle statistique de la régression simple z Chaque valeur observée yi est considérée comme une réalisation d’une variable aléatoire Yi définie par : Yi = axi + b + i où i est un terme aléatoire suivant une loi normale N(0, ). z On suppose que les aléas i sont indépendants les uns des autres. 21

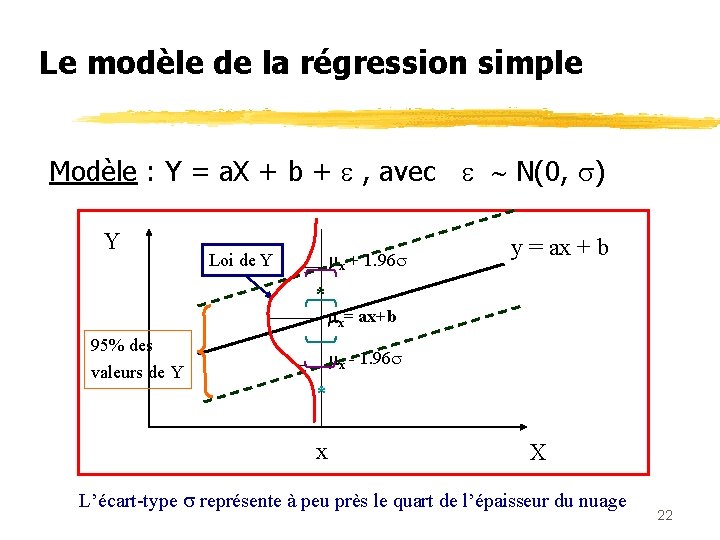
Le modèle de la régression simple Modèle : Y = a. X + b + , avec N(0, ) Y x + 1. 96 Loi de Y * x= ax+b 95% des valeurs de Y y = ax + b x - 1. 96 * x X L’écart-type représente à peu près le quart de l’épaisseur du nuage 22

Estimation de a, b et z. Estimation de a et b : z. Estimation de : 23

Prévision de Y z Modèle : Y = a. X + b + , avec N(0, ) x= E(Y | X = x) = ax + b z Problème 1 : Calculer une estimation et un intervalle de confiance au niveau de confiance 95 % de la moyenne x de Y lorsque X est fixé à x. z Soit y une future valeur de Y pour X fixé à x. z Problème 2 : Calculer une prévision et un intervalle contenant 95 % des futures valeurs de Y lorsque X est fixé à x. 24

Résultat pour x z Estimation de x = E(Y | X=x) : z Intervalle de confiance de x au niveau 95 % : Formule approchée : 25

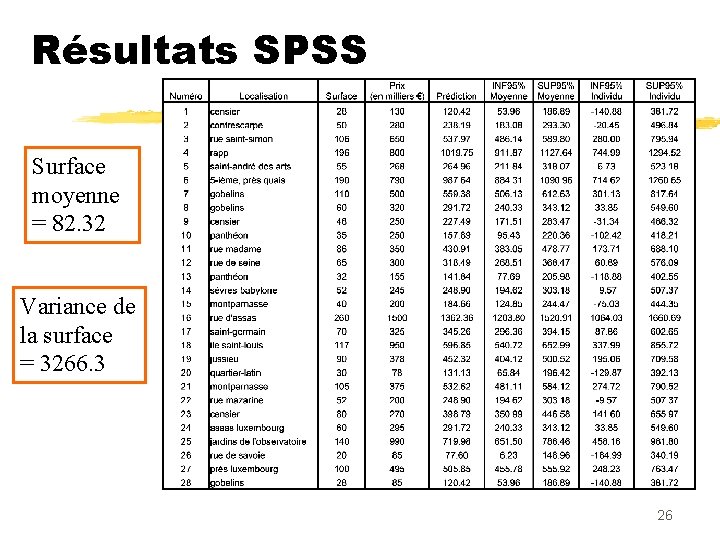
Résultats SPSS Surface moyenne = 82. 32 Variance de la surface = 3266. 3 26

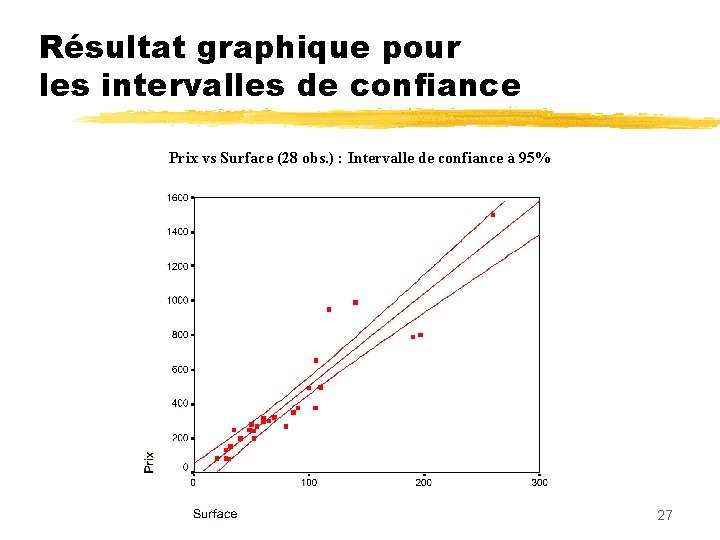
Résultat graphique pour les intervalles de confiance Prix vs Surface (28 obs. ) : Intervalle de confiance à 95% 27

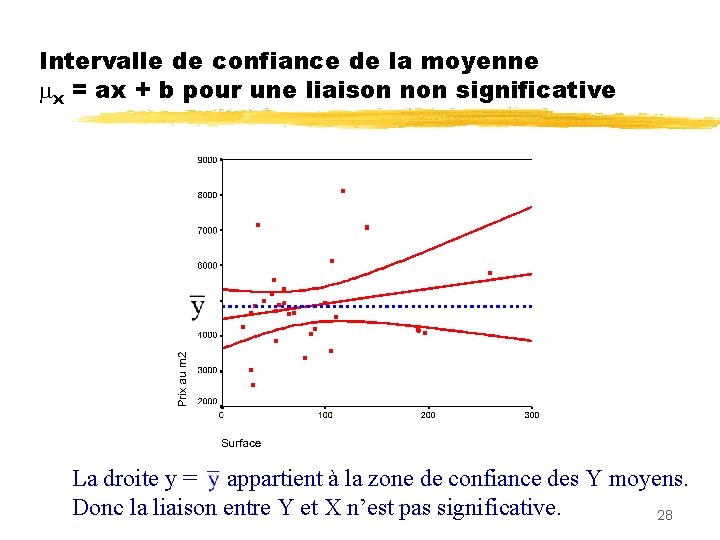
Intervalle de confiance de la moyenne x = ax + b pour une liaison non significative La droite y = appartient à la zone de confiance des Y moyens. Donc la liaison entre Y et X n’est pas significative. 28

Résultat pour y z Prévision de y pour x fixé : z Intervalle de prévision de y à 95 % pour x fixé : Formule approchée : 29

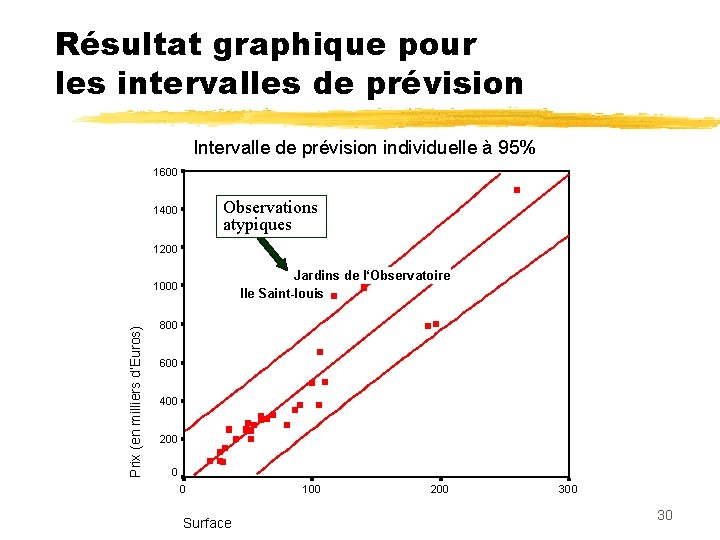
Résultat graphique pour les intervalles de prévision Intervalle de prévision individuelle à 95% 1600 Observations atypiques 1400 1200 Jardins de l‘Observatoire Ile Saint-louis Prix (en milliers d‘Euros) 1000 800 600 400 200 0 0 Surface 100 200 30

Observation atypique z Une observation est atypique (outlier) si elle n’appartient pas à son propre intervalle de prévision : z En utilisant la formule approchée : z Conclusion : Une observation i est un outlier si son résidu standardisé est supérieur à 2 en valeur absolue. 31

Résultats SPSS 32

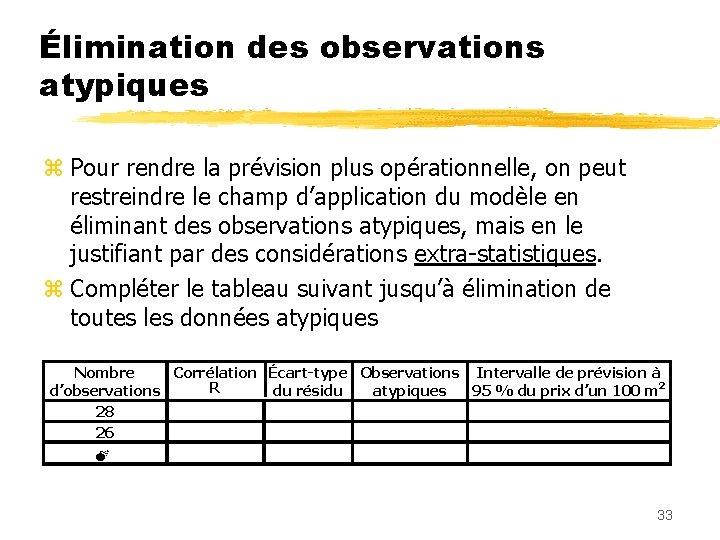
Élimination des observations atypiques z Pour rendre la prévision plus opérationnelle, on peut restreindre le champ d’application du modèle en éliminant des observations atypiques, mais en le justifiant par des considérations extra-statistiques. z Compléter le tableau suivant jusqu’à élimination de toutes les données atypiques Nombre Corrélation Écart-type Observations Intervalle de prévision à R d’observations du résidu atypiques 95 % du prix d’un 100 m 2 28 26 M 33