Il Teorema di Rolle Chi era Michel Rolle

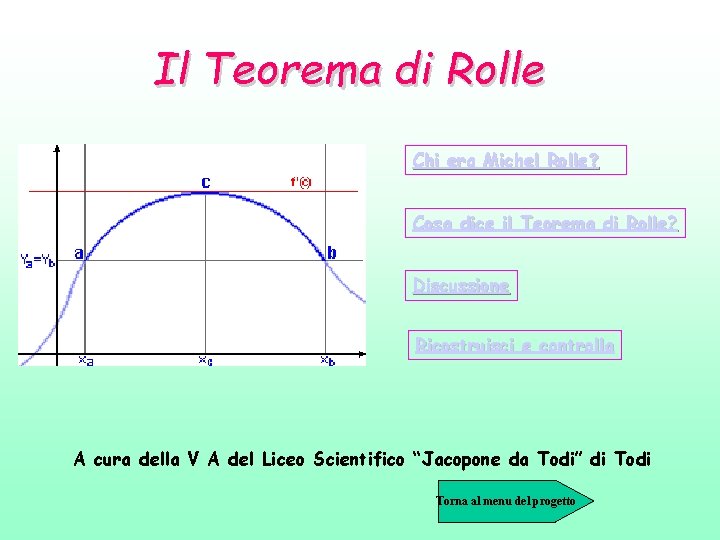
Il Teorema di Rolle Chi era Michel Rolle? Cosa dice il Teorema di Rolle? Discussione Ricostruisci e controlla A cura della V A del Liceo Scientifico “Jacopone da Todi” di Torna al menu del progetto

Michel Rolle nasce a Ambert nel 1652. Dal 1685 è membro dell’Accademia di Parigi come “géomètre pensionnaire”. Fu uno dei matematici più abili del suo tempo, tuttavia si distinse per un atteggiamento critico verso i nuovi metodi del calcolo differenziale che si andavano allora affermando, dando luogo a vivaci polemiche con P. Varignon e Jean Bernoulli e fu al centro di alcune polemiche contro l’Hôpital sul concetto di infinito e contro la geometria di Cartesio. La sua fama è dovuta soprattutto al Teorema che porta il suo nome: Teorema di Rolle, da lui dimostrato nel 1691. Le sue opere più importanti sono: “Traité d’algebre” 1690 e “Methode pour résudre les égalités” 1691.

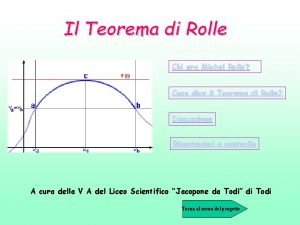
Data una funzione qualsiasi f(x), continua in un intervallo chiuso [a, b] e derivabile in ]a, b[ vi è almeno un punto c dell’intervallo [a, b] dove la derivata della funzione si annulla. IPOTESI: • f continua in [a, b] • f derivabile in ]a, b[ • f(a) = f(b) TESI: Esiste almeno un punto c in (a, b) tale che

Dimostrazione: ØSia f(x) continua in [a, b], derivabile in ]a, b[ , tale che f(a) = f(b). In virtù dell’ipotesi della continuità, vale il teorema Bolzano. Weierstrass, che ci assicura che esistono almeno un punto di massimo e un punto di minimo in [a, b]. • Supponiamo che entrambi cadano negli estremi a e b dell’intervallo. Ad esempio, se: Max = f(a) e min = f(b), in virtù dell’ipotesi che f(a) = f(b), si ha che Max = min e quindi f(x) è costante in tutto l’intervallo [a, b]. Quindi f’(x) = 0 in tutto [a, b].

• Supponiamo ora che almeno uno dei due, il massimo o il minimo, cada nell’intervallo ]a, b[. Ad esempio, se: Max = f(c), con c appartenente all’intervallo ]a, b[ , allora il rapporto incrementale sinistro mentre il rapporto incrementale destro è

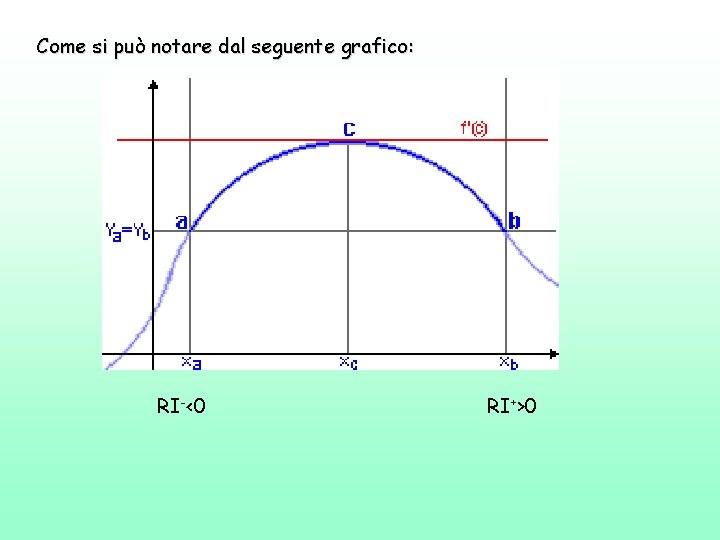
Come si può notare dal seguente grafico: RI-<0 RI+>0

In virtù dell’inverso del Teorema della permanenza del segno ne segue che, il lim ≥ 0 e lim ≤ 0 E in virtù dell’ipotesi della derivabilità, i due limiti devono essere uguali e quindi: 0 lim = lim =

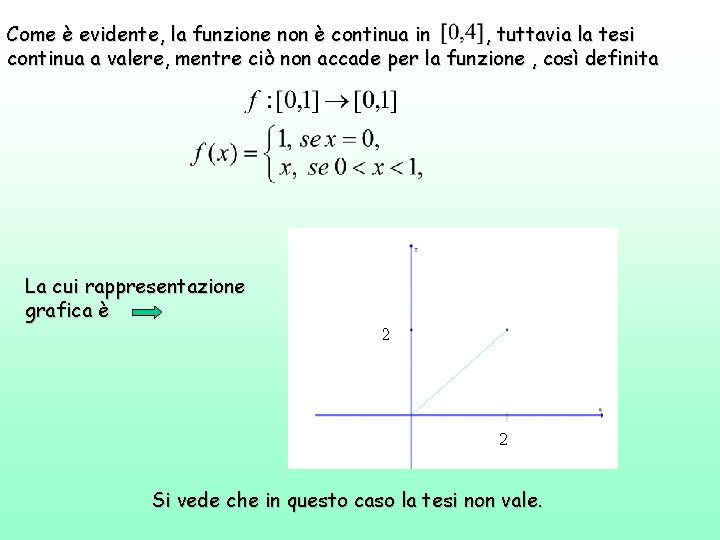
Esaminiamo le ipotesi del Teorema di Rolle e analizziamo cosa accade se cadono le ipotesi. Se cade l’ipotesi di continuità della funzione in [a, b], la tesi continua a valere solo in alcuni casi. Consideriamo ad esempio così definita: La cui rappresentazione grafica è la seguente

Come è evidente, la funzione non è continua in , tuttavia la tesi continua a valere, mentre ciò non accade per la funzione , così definita La cui rappresentazione grafica è Si vede che in questo caso la tesi non vale.

Si possono fare considerazioni analoghe a quanto accade per la continuità, cioè, se cade l’ipotesi che f sia derivabile in ]a, b[, la tesi del Teorema di Rolle continua a valere solo in alcuni casi. Infatti, se si considera la funzione x f(x)= - x - 1 se – 2 ≤ x ≤ -1 0 se -1 < x < 1 x - 1 se 1 ≤ x ≤ 2 così definita

rappresentata così La funzione f(x) è continua in [-2, 2]; f(-2)=f( 2) = 1, ma non è derivabile in x = -1 e x = 1; tuttavia esistono infiniti punti x tra ]-1, 1[ in cui f’(x) = 0.

Di nuovo si ritrova che la tesi continua a valere soltanto in alcuni casi. Infatti, se si considera la funzione è continua in definita da , derivabile in , ma e la tesi del Teorema di Rolle non vale. Se invece si considera la funzione , in tal caso, sebbene risulta che si ha che definita da nel punto

Utilizzando il Teorema di Rolle, si può affermare che se l’equazione xn + an-1 xn-1 + … +a 1 x + a 0 = 0 ammette radici reali, allora, fra due di esse, l’equazione nxn-1+ (n-1)xn-2 + … + a 1 =0 ammette almeno una radice. Infatti, poiché f (x)= xn + an-1 xn-1 + … + a 1 x + a 0 1) è continua in R 2) è derivabile in R, 3) se x 1 e x 2 sono radici di f (x), allora f(x 1) = f(x 2) = 0 Per il Teorema di Rolle almeno f ( ] x 1, x 2 [ tale che f ( ) = nxn-1+ (n-1)xn-2+ … + a 1 = 0. ) = 0 cioè

Attraverso il Teorema di Rolle, si riesce a dire, ad esempio, che l’equazione 3 x 5+ 15 x – 12 = 0 ammette una sola radice reale. Infatti, il Teorema fondamentale dell’algebra ci assicura che l’equazione, essendo di grado dispari, ha almeno una radice reale. Se per assurdo esistessero due radici x 1 , x 2 reali tali che f(x 1) = f(x 2) = 0, allora dovrebbe esistere un x 0 appartenente all’intervallo aperto ] x 1, x 2[ tale che la derivata prima calcolata nel punto x 0 è uguale a zero, ma f’(x)= 15 x 4 + 15 non si annulla mai nel campo reale.