TEOREMA DE PITGORAS TEOREMA DE PITGORAS Pitgoras um

TEOREMA DE PITÁGORAS Pitágoras, um dos maiores filósofos da Europa antiga, nasceu cerca de

ALGUMAS DEMONSTRAÇÕES DO TEOREMA DE PITÁGORAS Considere-se um triângulo retângulo cujos lados medem, numa

CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Num dos quadrados constroem-se 4 triângulos

CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • No segundo quadrado, dois quadrados e

CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Ora, mas em cada figura, o

CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Ora se compararmos as áreas dos

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Desenha um triângulo retângulo [ABC], qualquer, retângulo

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Em seguida constrói os quadrados de lados

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Em seguida, desenha as diagonais do quadrado

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS Por O traça dois segmentos de reta paralelos

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS O quadrado ficou dividido em 4 partes que

Slides: 13

Download presentation

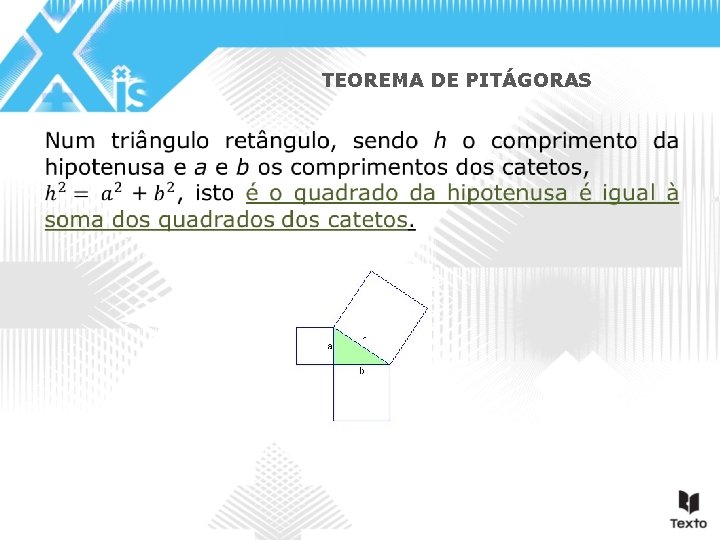
TEOREMA DE PITÁGORAS

TEOREMA DE PITÁGORAS Pitágoras, um dos maiores filósofos da Europa antiga, nasceu cerca de 580 anos a. C. , em Samos, uma ilha do mar Egeu, ou, segundo alguns, em Sidon, na Fenícia.

TEOREMA DE PITÁGORAS

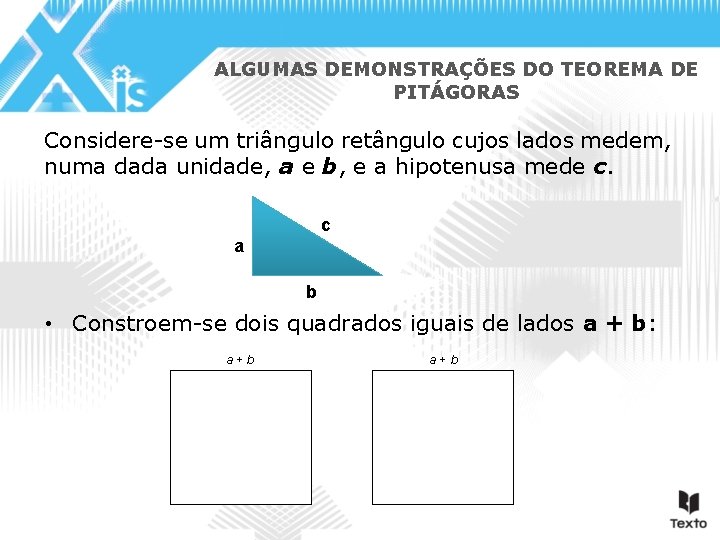
ALGUMAS DEMONSTRAÇÕES DO TEOREMA DE PITÁGORAS Considere-se um triângulo retângulo cujos lados medem, numa dada unidade, a e b, e a hipotenusa mede c. c a b • Constroem-se dois quadrados iguais de lados a + b: a+b

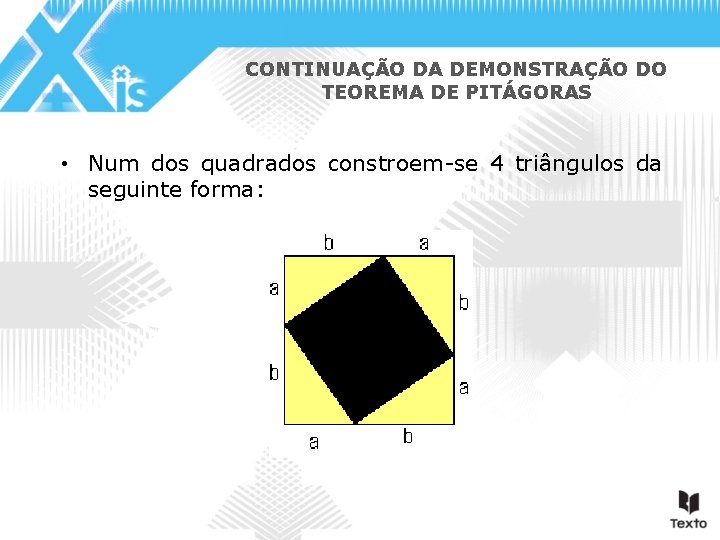
CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Num dos quadrados constroem-se 4 triângulos da seguinte forma:

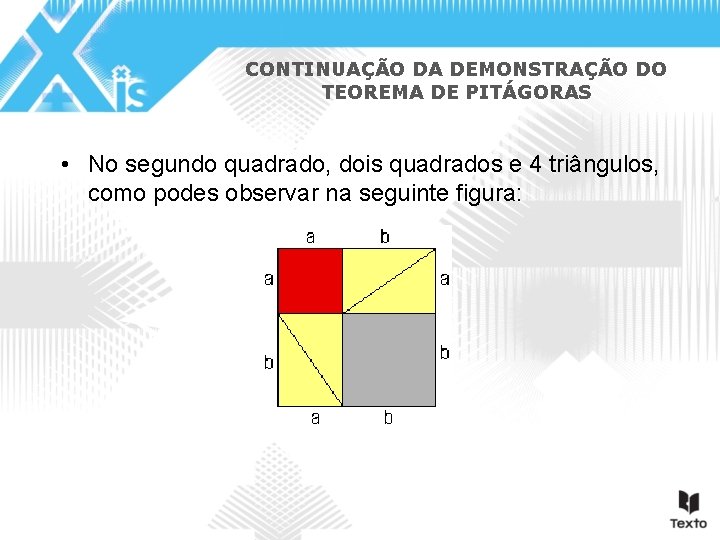
CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • No segundo quadrado, dois quadrados e 4 triângulos, como podes observar na seguinte figura:

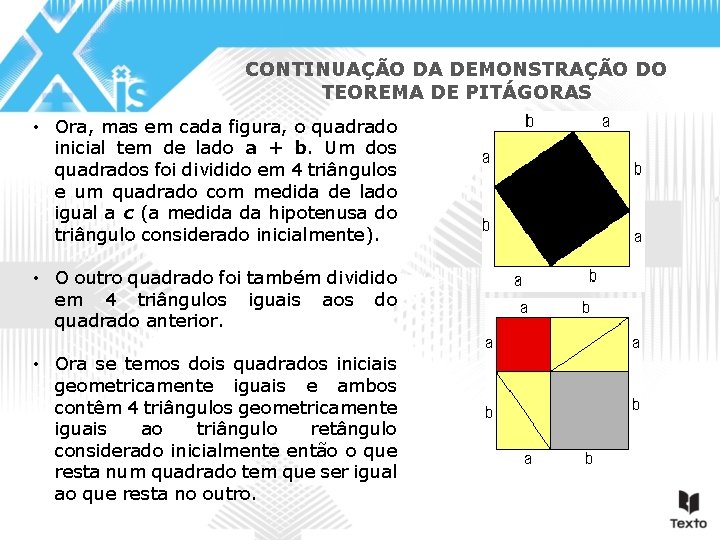
CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Ora, mas em cada figura, o quadrado inicial tem de lado a + b. Um dos quadrados foi dividido em 4 triângulos e um quadrado com medida de lado igual a c (a medida da hipotenusa do triângulo considerado inicialmente). • O outro quadrado foi também dividido em 4 triângulos iguais aos do quadrado anterior. • Ora se temos dois quadrados iniciais geometricamente iguais e ambos contêm 4 triângulos geometricamente iguais ao triângulo retângulo considerado inicialmente então o que resta num quadrado tem que ser igual ao que resta no outro.

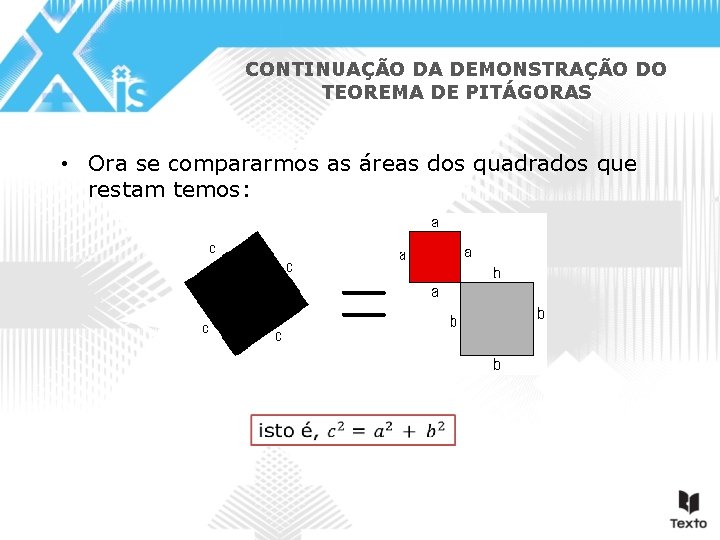
CONTINUAÇÃO DA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Ora se compararmos as áreas dos quadrados que restam temos:

OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Desenha um triângulo retângulo [ABC], qualquer, retângulo em A. C A B

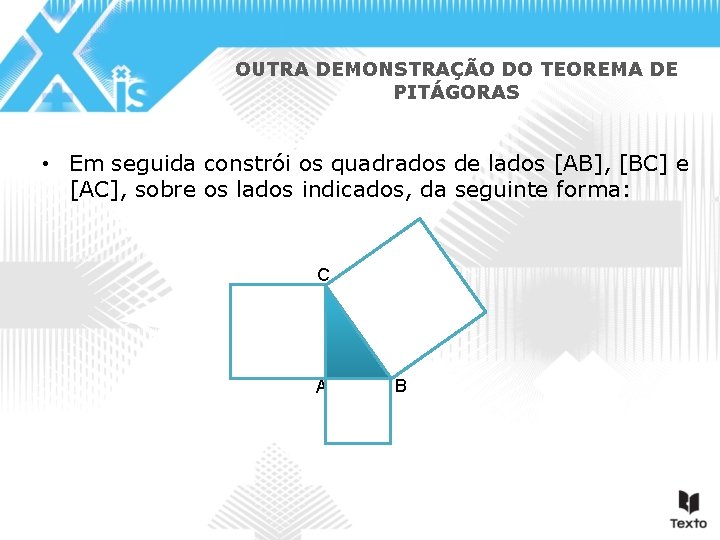
OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Em seguida constrói os quadrados de lados [AB], [BC] e [AC], sobre os lados indicados, da seguinte forma: C A B

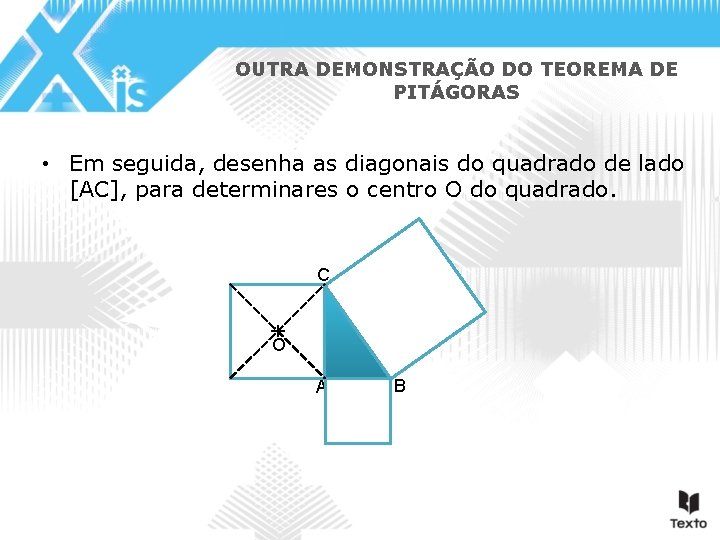
OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS • Em seguida, desenha as diagonais do quadrado de lado [AC], para determinares o centro O do quadrado. C O A B

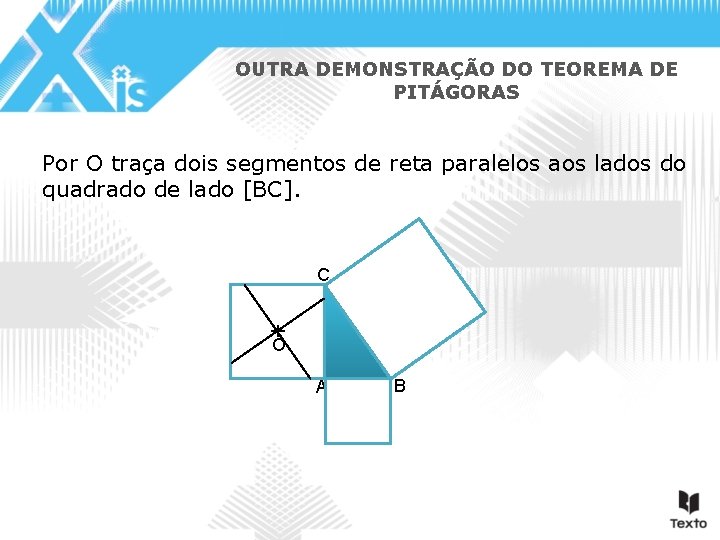
OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS Por O traça dois segmentos de reta paralelos aos lados do quadrado de lado [BC]. C O A B

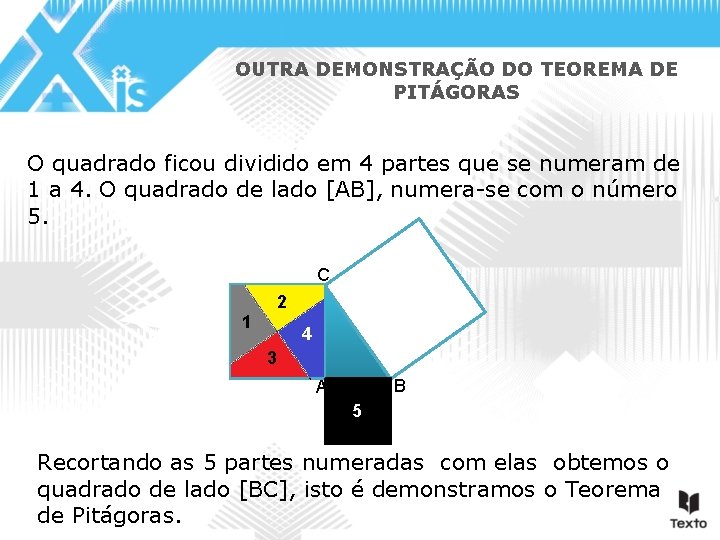
OUTRA DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS O quadrado ficou dividido em 4 partes que se numeram de 1 a 4. O quadrado de lado [AB], numera-se com o número 5. C 2 1 4 3 B A 5 Recortando as 5 partes numeradas com elas obtemos o quadrado de lado [BC], isto é demonstramos o Teorema de Pitágoras.