Rgression linaire simple et multiple 1 Exemple Une

Régression linéaire simple et multiple 1

Exemple • Une entreprise faisant du marketing direct en ligne aimerait construire un modèle pour identifier les clients les plus susceptibles d’acheter des produits de leur prochain catalogue qui doit être envoyé le mois prochain. Ainsi, les clients qui seront identifiés par le modèle comme ayant peu de chance d’acheter seront exclu de la prochaine liste d’envoi. 2

Exemple (suite) • Au cours de la dernière année, l’entreprise a recueilli l’information suivante dans sa base de données pour un sousensemble de ses clients (fichier régression. xls): – nombre total d’envois postaux, – nombre total de commandes (achats) reçues, – montant total (en dollars) des achats jusqu’à aujourd’hui (variable: Tot_doll), – montant (en dollars) des commandes 12 derniers mois. – nombre de mois écoulé depuis le dernier achat – sexe du client (variable: sexe, 0=femme 1=homme). 3

Exemple (suite) • Malheureusement, l’entreprise n’a pas pensé inclure dans sa base de données si les clients ont fait un achat (oui ou non) après chacun des envois postaux. • Cependant elle émet l’hypothèse que le ratio nombre total de commandes reçues sur le nombre total d’envois est une bonne mesure de la probabilité d’un achat. Cette variable servira de variable dépendante (Y). • Les autres variables serviront de variables explicatives dans le modèle. • Comment procéderiez-vous? 4

Introduction: • Un des objectifs principaux de la statistique est d ’expliquer la variabilité que l ’on observe dans les données. • La régression linéaire (ou les modèles linéaires) est un outil statistique TRÈS UTILISÉ pour étudier la présence d ’une relation entre une variable dépendante Y (quantitative et continue) et une ou plusieurs variables indépendantes X 1, X 2, …, Xp (qualitatives et/ou quantitatives). 5

Un modèle de régression peut servir à répondre à un des 3 objectifs suivants: • Décrire (données provenant d ’études nonexpérimentales c. -à-d. on observe la réalité telle qu’elle est). • Confronter des hypothèses (données provenant d ’études expérimentales contrôlées). • Prédire (si on aime le risque!!). 6

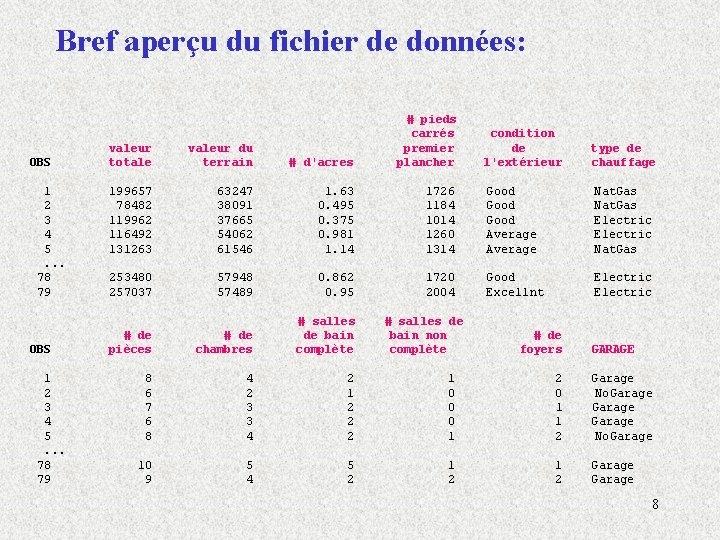
Exemple: Nous sommes intéressés à savoir quels sont les facteurs importants qui influencent ou déterminent la valeur d ’une propriété et de construire un modèle qui nous aidera à évaluer cette valeur selon ces facteurs. Pour ce faire, nous avons obtenu la valeur totale pour un échantillon de 79 propriétés dans une région donnée. Les variables suivantes ont également été recueillies pour chacune des propriétés: 7

Bref aperçu du fichier de données: OBS 1 2 3 4 5. . . 78 79 valeur totale valeur du terrain # d'acres # pieds carrés premier plancher 199657 78482 119962 116492 131263 63247 38091 37665 54062 61546 1. 63 0. 495 0. 375 0. 981 1. 14 253480 257037 57948 57489 0. 862 0. 95 # de pièces # de chambres # salles de bain complète 8 6 7 6 8 4 2 3 3 4 2 1 2 2 2 1 0 0 0 1 2 0 1 1 2 Garage No. Garage 10 9 5 4 5 2 1 2 Garage condition de l'extérieur type de chauffage 1726 1184 1014 1260 1314 Good Average Nat. Gas Electric Nat. Gas 1720 2004 Good Excellnt Electric # salles de bain non complète # de foyers GARAGE 8

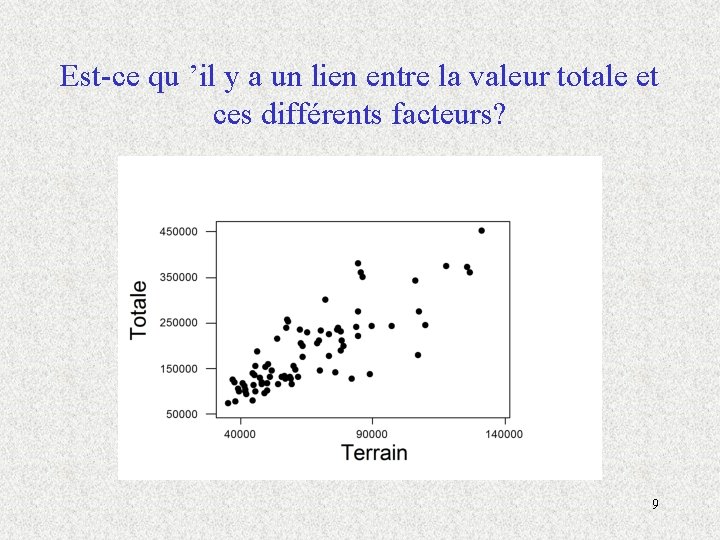
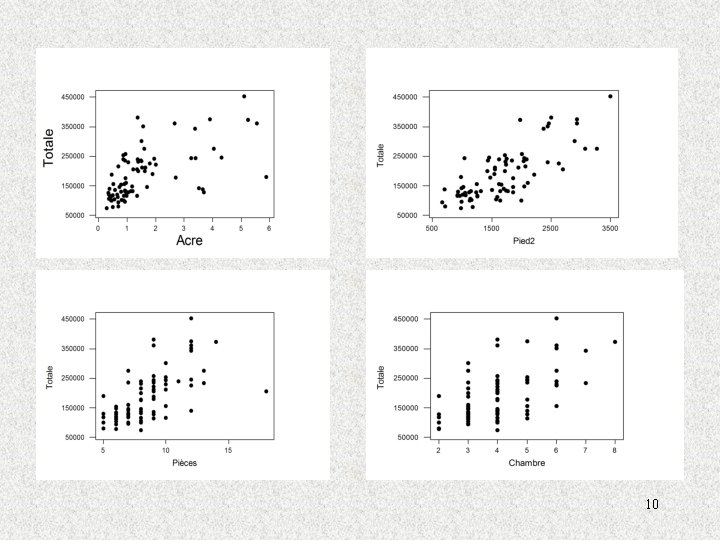
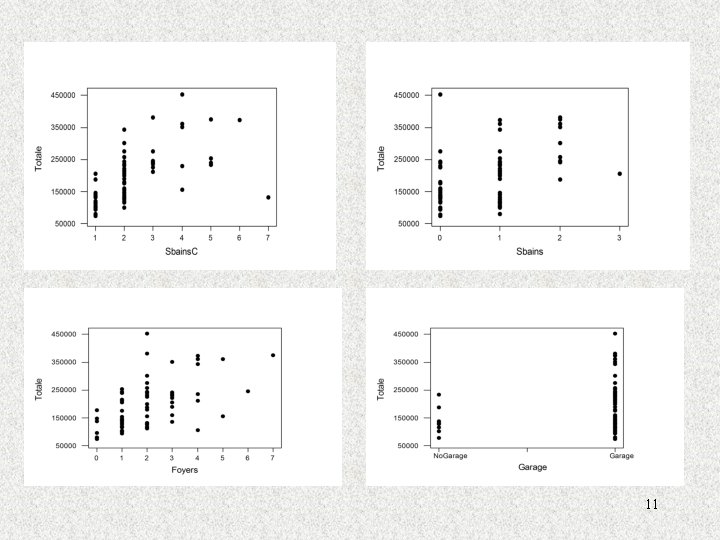
Est-ce qu ’il y a un lien entre la valeur totale et ces différents facteurs? 9

10

11

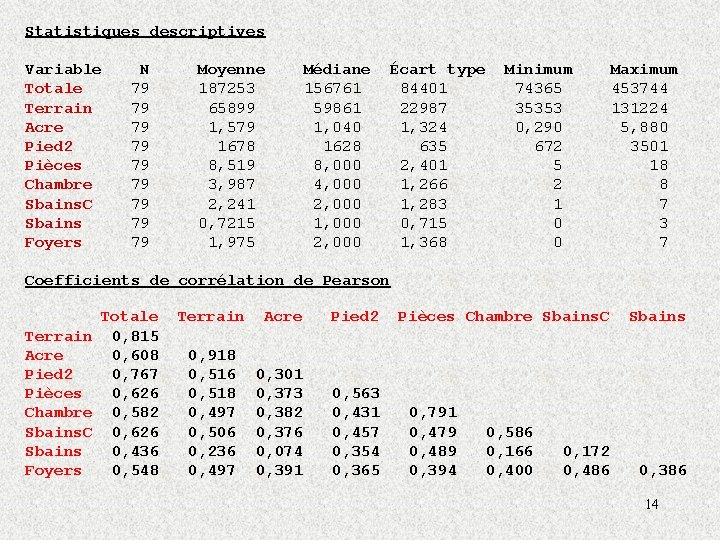
Le coefficient de corrélation r de Pearson sert à mesurer l’intensité de la relation linéaire entre deux variables quantitatives. • Le coefficient de corrélation r prendra des valeurs entre -1 et 1. • S ’il existe une relation linéaire parfaite entre X et Y alors r = 1 (r =1 si X et Y varient dans le même sens et r = -1 si X varie dans le sens opposé à Y). • Si r = 0, ceci indique qu ’il n ’y a pas de lien linéaire entre X et Y. • Plus la valeur de r s ’éloigne de 0 pour s ’approcher de 1 plus l ’intensité du lien linéaire entre X et Y grandit. 12

Statistiques descriptives Variable Totale Terrain Acre Pied 2 Pièces Chambre Sbains. C Sbains Foyers N 79 79 79 Moyenne 187253 65899 1, 579 1678 8, 519 3, 987 2, 241 0, 7215 1, 975 Médiane 156761 59861 1, 040 1628 8, 000 4, 000 2, 000 1, 000 2, 000 Écart type 84401 22987 1, 324 635 2, 401 1, 266 1, 283 0, 715 1, 368 Minimum 74365 35353 0, 290 672 5 2 1 0 0 Maximum 453744 131224 5, 880 3501 18 8 7 3 7 Coefficients de corrélation de Pearson Totale Terrain 0, 815 Acre 0, 608 Pied 2 0, 767 Pièces 0, 626 Chambre 0, 582 Sbains. C 0, 626 Sbains 0, 436 Foyers 0, 548 Terrain Acre Pied 2 0, 918 0, 516 0, 518 0, 497 0, 506 0, 236 0, 497 0, 301 0, 373 0, 382 0, 376 0, 074 0, 391 0, 563 0, 431 0, 457 0, 354 0, 365 Pièces Chambre Sbains. C 0, 791 0, 479 0, 489 0, 394 0, 586 0, 166 0, 400 0, 172 0, 486 Sbains 0, 386 14

Régression linéaire simple • Pour décrire une relation linéaire entre deux variables quantitatives ou encore pour pouvoir prédire Y pour une valeur donnée de X, nous utilisons une droite de régression: • Y = 0 + 1 X + • Puisque tout modèle statistique n’est qu’une approximation (nous espérons la meilleure possible!!), il y a toujours une erreur, notée dans le modèle, car le lien linéaire n’est jamais parfait. • S ’il y avait une relation linéaire parfaite entre Y et X, le terme d ’erreur serait toujours égale à 0, et toute la variabilité de Y serait expliquée par la variable indépendante X. 16

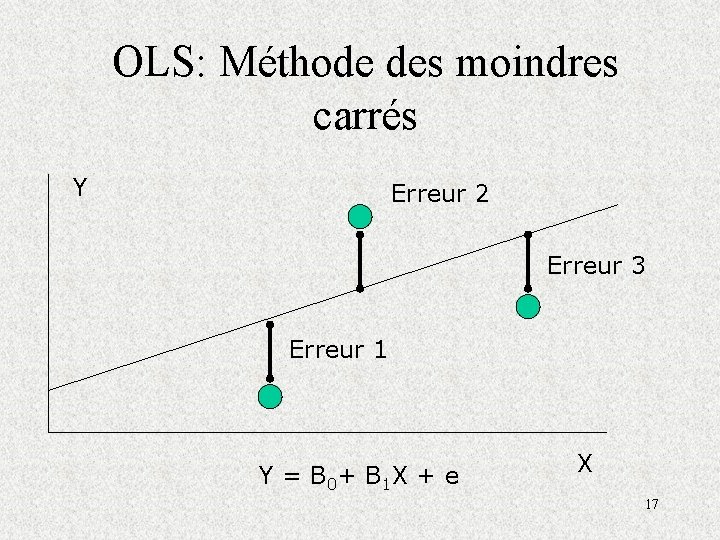
OLS: Méthode des moindres carrés Y Erreur 2 Erreur 3 Erreur 1 Y = B 0+ B 1 X + e X 17

• Donc, pour une valeur donnée de X, nous aimerions estimer Y. • Ainsi, à l’aide des données de l’échantillon nous estimerons les paramètres 0 et 1 du modèle de régression de façon à minimiser la somme des carrés des erreurs. • Le coefficient de corrélation au carré est appelé coefficient de détermination et nous indique le pourcentage de la variabilité de Y expliquée par X: R 2 = 1 - (n-2)/(n-1){Se /Sy}2, où Se est l’écart type des erreurs et Sy est l’écart type de Y. 18

• On peut également utiliser le coefficient de détermination ajusté pour nous indiquer le pourcentage de la variabilité de Y expliquée par X: R 2 ajusté = 1 - {Se/Sy}2. 19

Exemple de régressions linéaires simples: MODÈLE 1. Regression Analysis The regression equation is Totale = 16209 + 102 Pied 2 Predictor Constant Pied 2 S = 54556 Coef 16209 101, 939 St. Dev 17447 9, 734 R-Sq = 58, 8% T 0, 93 10, 47 P 0, 356 0, 000 R-Sq(adj) = 58, 2% Analysis of Variance Source Regression Residual Error Total DF SS MS 1 3, 26460 E+11 77 2, 29181 E+11 2976374177 78 5, 55641 E+11 F 109, 68 P 0, 000 20

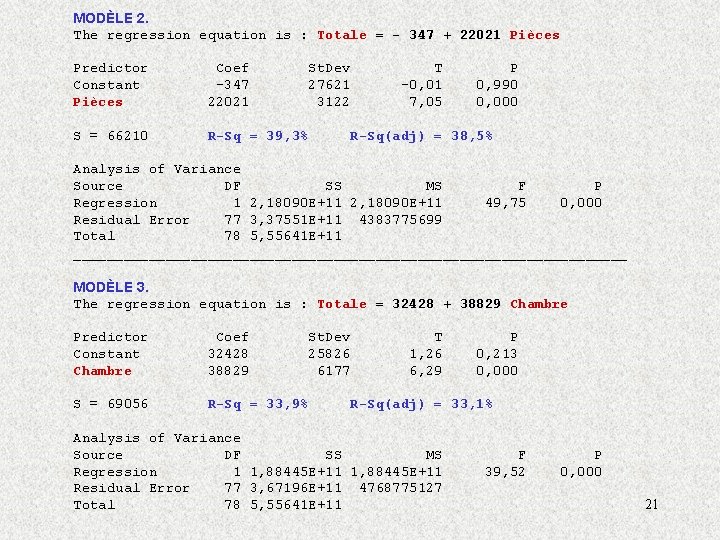
MODÈLE 2. The regression equation is : Totale = - 347 + 22021 Pièces Predictor Constant Pièces Coef -347 22021 St. Dev 27621 3122 S = 66210 R-Sq = 39, 3% T -0, 01 7, 05 P 0, 990 0, 000 R-Sq(adj) = 38, 5% Analysis of Variance Source DF SS MS F P Regression 1 2, 18090 E+11 49, 75 0, 000 Residual Error 77 3, 37551 E+11 4383775699 Total 78 5, 55641 E+11 _________________________________ MODÈLE 3. The regression equation is : Totale = 32428 + 38829 Chambre Predictor Constant Chambre Coef 32428 38829 St. Dev 25826 6177 S = 69056 R-Sq = 33, 9% T 1, 26 6, 29 P 0, 213 0, 000 R-Sq(adj) = 33, 1% Analysis of Variance Source DF SS MS Regression 1 1, 88445 E+11 Residual Error 77 3, 67196 E+11 4768775127 Total 78 5, 55641 E+11 F 39, 52 P 0, 000 21

• Modèle 1: – valeur totale = 16209 + 102*( # pieds carrés ). – R 2 = 58, 8%. Donc 58, 8% de la variabilité de la valeur totale est expliquée par le # pieds carrés. • Modèle 2: – valeur totale = -347 + 22021*( # pièces ). – R 2 = 39, 3%. Donc 39, 3% de la variabilité de la valeur totale est expliquée par le # pièces. • Modèle 3: – valeur totale = 32428 + 38829*( # chambres ). – R 2 = 33, 9%. Donc 33, 9% de la variabilité de la valeur totale est expliquée par le # chambres. 22

Parmi les 3 modèles précédents, lequel choisiriez vous et pourquoi? Le modèle 1 car il a la plus grande valeur de R 2. 23

Intervalle de confiance au niveau 1 - pour la moyenne des valeurs de Y pour une valeur spécifique de X: • Pour le modèle 1 et une valeur de X=1500 pi 2 on obtient l ’estimation ponctuelle suivante: – est. valeur totale = 16 209 + 102*1500 = 169 117$ – intervalle de confiance à 95% pour la moyenne de la valeur totale pour les propriétés de 1500 pi 2 : [156 418, 181 817] 24

Intervalle de confiance au niveau 1 - pour une nouvelle valeur de Y (prévision) étant donné une valeur spécifique de X: • Pour le modèle 1 et une valeur de X=1500 pi 2 on obtient l’estimation ponctuelle suivante: – est. valeur totale = 16 209 + 101, 939*1500 = 169 117$ – intervalle de confiance à 95% pour une valeur totale prédite lorsque la superficie du premier plancher est de 1500 pi 2 : [59 742, 278 492] • L ’intervalle de confiance pour une valeur prédite est toujours plus grand que pour la moyenne des valeurs de Y pour un X spécifique. 25

Régression linéaire multiple • Il est fort possible que la variabilité de la variable dépendante Y soit expliquée non pas par une seule variable indépendante X mais plutôt par une combinaison linéaire de plusieurs variables indépendantes X 1, X 2, …, Xp. • Dans ce cas le modèle de régression multiple est donné par: Y = 0 + 1 X 1 + 2 X 2 + … + p. Xp + • Aussi, à l’aide des données de l’échantillon nous estimerons les paramètres 0, 1, …, p du modèle de régression de façon à minimiser la somme des carrés des erreurs. 26

• Le coefficient de corrélation multiple R 2 , aussi appelé coefficient de détermination, nous indique le pourcentage de la variabilité de Y expliquée par les variables indépendantes X 1, X 2, …, Xp. • Lorsqu’on ajoute une ou plusieurs variables indépendantes dans le modèle, le coefficient R 2 augmente. • La question est de savoir si le coefficient R 2 augmente de façon significative. • Notons qu’on ne peut avoir plus de variables indépendantes dans le modèle qu’il y a d ’observations dans l’échantillon (règle générale: n 5 p). 27

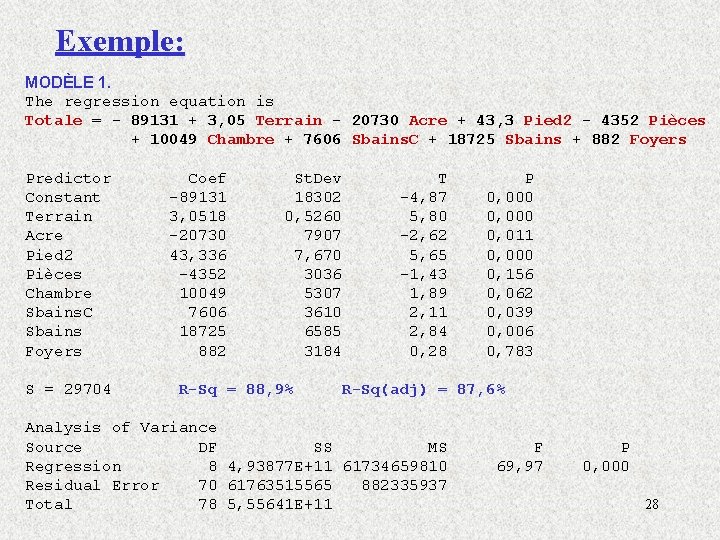
Exemple: MODÈLE 1. The regression equation is Totale = - 89131 + 3, 05 Terrain - 20730 Acre + 43, 3 Pied 2 - 4352 Pièces + 10049 Chambre + 7606 Sbains. C + 18725 Sbains + 882 Foyers Predictor Constant Terrain Acre Pied 2 Pièces Chambre Sbains. C Sbains Foyers S = 29704 Coef -89131 3, 0518 -20730 43, 336 -4352 10049 7606 18725 882 St. Dev 18302 0, 5260 7907 7, 670 3036 5307 3610 6585 3184 R-Sq = 88, 9% T -4, 87 5, 80 -2, 62 5, 65 -1, 43 1, 89 2, 11 2, 84 0, 28 P 0, 000 0, 011 0, 000 0, 156 0, 062 0, 039 0, 006 0, 783 R-Sq(adj) = 87, 6% Analysis of Variance Source DF SS MS Regression 8 4, 93877 E+11 61734659810 Residual Error 70 61763515565 882335937 Total 78 5, 55641 E+11 F 69, 97 P 0, 000 28

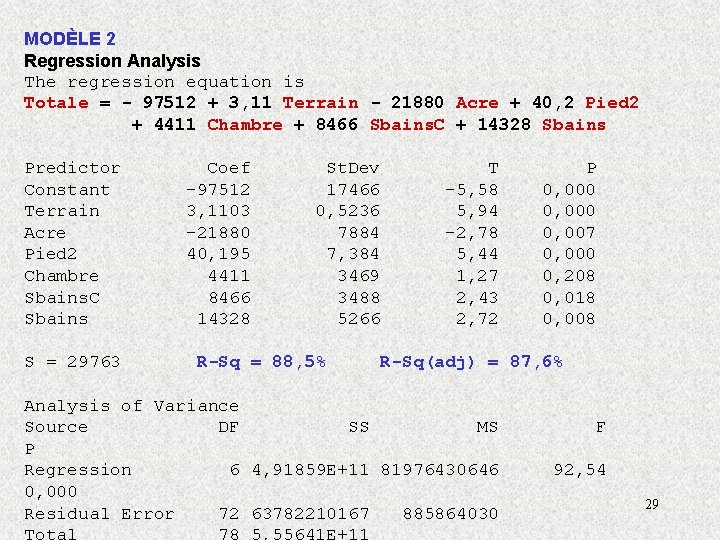
MODÈLE 2 Regression Analysis The regression equation is Totale = - 97512 + 3, 11 Terrain - 21880 Acre + 40, 2 Pied 2 + 4411 Chambre + 8466 Sbains. C + 14328 Sbains Predictor Constant Terrain Acre Pied 2 Chambre Sbains. C Sbains S = 29763 Coef -97512 3, 1103 -21880 40, 195 4411 8466 14328 St. Dev 17466 0, 5236 7884 7, 384 3469 3488 5266 R-Sq = 88, 5% T -5, 58 5, 94 -2, 78 5, 44 1, 27 2, 43 2, 72 P 0, 000 0, 007 0, 000 0, 208 0, 018 0, 008 R-Sq(adj) = 87, 6% Analysis of Variance Source DF SS MS P Regression 6 4, 91859 E+11 81976430646 0, 000 Residual Error 72 63782210167 885864030 F 92, 54 29

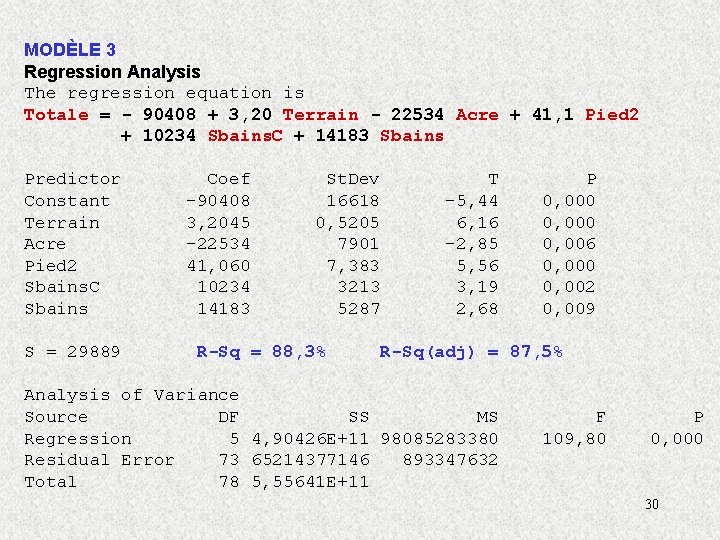
MODÈLE 3 Regression Analysis The regression equation is Totale = - 90408 + 3, 20 Terrain - 22534 Acre + 41, 1 Pied 2 + 10234 Sbains. C + 14183 Sbains Predictor Constant Terrain Acre Pied 2 Sbains. C Sbains S = 29889 Coef -90408 3, 2045 -22534 41, 060 10234 14183 St. Dev 16618 0, 5205 7901 7, 383 3213 5287 R-Sq = 88, 3% T -5, 44 6, 16 -2, 85 5, 56 3, 19 2, 68 P 0, 000 0, 006 0, 000 0, 002 0, 009 R-Sq(adj) = 87, 5% Analysis of Variance Source DF SS MS Regression 5 4, 90426 E+11 98085283380 Residual Error 73 65214377146 893347632 Total 78 5, 55641 E+11 F 109, 80 P 0, 000 30

Modèle sans la superficie du terrain ( # d ’acres ) à cause de la multicolinéarité avec la valeur du terrain. MODÈLE 4 The regression equation is Totale = - 55533 + 1, 82 Terrain + 49, 8 Pied 2 + 11696 Sbains. C + 18430 Sbains Predictor Constant Terrain Pied 2 Sbains. C Sbains S = 31297 Coef -55533 1, 8159 49, 833 11696 18430 St. Dev 11783 0, 1929 7, 028 3321 5312 R-Sq = 87, 0% T -4, 71 9, 42 7, 09 3, 52 3, 47 P 0, 000 0, 001 R-Sq(adj) = 86, 3% Analysis of Variance Source DF SS MS Regression 4 4, 83160 E+11 1, 20790 E+11 Residual Error 74 72481137708 979474834 Total 78 5, 55641 E+11 F 123, 32 P 0, 000 31

Parmi les 4 modèles précédents, lequel choisiriez vous et pourquoi? • Probablement le modèle 4 car toutes les variables indépendantes sont significatives au niveau 5% (c. -à-d. p-value < 5% pour chaque dans le modèle) et bien que le R 2 soit plus petit, il n ’est que marginalement plus petit. De plus tous les coefficients du modèle ont « du sens » ! • Dans le modèle 1 les variables ‘ # de pièces ’ et ‘ # de foyers ’ ne sont pas statistiquement significatives au niveau 5% (p-value > 5%). La variable ‘ # de chambres ’ est à la limite avec un p-value = 0, 0624. 32

Parmi les 4 modèles précédents, lequel choisiriez vous et pourquoi? • Dans le modèle 2 la variable ‘ # de chambres ’ n ’est pas statistiquement significative au niveau 5%. • Dans le modèle 3 (et les modèles précédents), le coefficient de la variable ‘ # d ’acres ’ est négatif ce qui est à l ’encontre du « bon sens » et de ce qu ’on a observé sur le diagramme de dispersion et le coefficient de corrélation de Pearson positif (r = 0, 608). • Le coefficient négatif pour la variable ‘ # d ’acres ’ dans les modèles 1 à 3 est causé par le fait qu ’il y a une forte relation linéaire entre la valeur du terrain et la superficie du terrain (r = 0, 918); problème de multicolinéarité. 33

Comment choisir un modèle de régression linéaire parmi tous les modèles possibles? Il existe plusieurs techniques: • sélection pas à pas en ajoutant une variable à la fois et en commençant par la plus significative (stepwise, forward). • sélection à partir du modèle incluant toutes les variables et en enlevant une variable à la fois en commençant par la moins significative (backward). • faire tous les modèles possibles et choisir le meilleur sous-ensemble de variables (best subset) selon certains critères spécifiques (ex: R 2 ajusté, Cp de Mallow. ) 34

Exemple de sélection parmi les meilleurs sous-ensembles: Best Subsets Regression : Response is Totale T e r r a i n A c r e P i e d 2 P i è c e s C h a m b r e S b a i n s C S b a i n s F o y e r s Vars R-Sq Adj. R-Sq C-p s 1 1 1 66, 4 58, 8 39, 3 65, 9 58, 2 38, 5 136, 8 184, 7 307, 6 49262 54556 66210 X 2 2 2 82, 7 78, 8 74, 4 82, 2 78, 3 73, 7 35, 9 60, 3 88, 1 35564 39343 43244 X X X 3 3 3 85, 6 84, 8 85, 0 84, 2 19, 5 24, 9 32637 33521 33591 X X X X 4 4 4 87, 1 87, 0 86, 6 86, 4 86, 3 85, 9 12, 2 13, 1 15, 2 31115 31297 31682 X X X 5 5 5 88, 3 87, 6 87, 4 87, 5 86, 7 86, 5 6, 9 11, 2 12, 4 29889 30744 30979 X X X X X 6 6 6 88, 5 88, 3 87, 6 87, 3 8, 6 8, 9 29763 30030 30096 X X X X X 7 7 7 88, 9 88, 6 88, 3 87, 8 87, 4 87, 2 7, 1 9, 1 10, 6 29510 29924 30240 X X X X X X 8 88, 9 87, 6 9, 0 29704 X X X X X 35

Sélection du modèle sans la variable # d ’acres Best Subsets Regression : Response is Totale T e r r a i n P i e d 2 P i è c e s C h a m b r e S b a i n s C S b a i n s F o y e r s Vars R-Sq Adj. R-Sq C-p s 1 1 1 66, 4 58, 8 39, 3 65, 9 58, 2 38, 5 120, 6 164, 9 278, 3 49262 54556 66210 X 2 2 2 82, 7 72, 5 82, 2 71, 9 71, 8 27, 6 86, 0 86, 8 35564 44704 44813 X X 3 3 3 84, 8 84, 0 84, 2 83, 3 17, 2 17, 6 22, 3 33521 33591 34467 X X X 4 4 4 87, 0 86, 1 85, 3 86, 3 85, 3 84, 5 6, 9 12, 1 16, 5 31297 32352 33226 X X X 5 5 5 87, 3 87, 0 86, 4 86, 1 6, 9 8, 5 8, 9 31100 31439 31509 X X X X 6 6 6 87, 8 87, 3 87, 0 86, 8 86, 3 85, 9 6, 1 8, 7 10, 5 30707 31264 31656 X X X X X 7 87, 8 86, 6 8, 0 30908 X X X X X 36

Le choix du meilleur modèle se fait selon la combinaison: • La plus grande valeur de R 2 ajusté pour le nombre de variables dans le modèle. • La plus petite valeur de Cp. • Pour les modèles avec R 2 ajusté et Cp comparables, on choisira le modèle qui a le plus de « sens » selon les experts dans le domaine. • Pour les modèles avec R 2 ajusté et Cp comparables, le modèle avec les variables indépendantes les plus faciles et moins coûteuses à mesurer. • La validité du modèle. 37

Intervalle de confiance au niveau 1 - pour la moyenne de Y et une nouvelle valeur de Y (prévision) étant donné une combinaison de valeurs spécifiques pour X 1, X 2, …, Xp. • Pour le modèle 4 et une propriété avec terrain= 65 000$, pi 2 = 1500, 2 salles de bain complète et 1 non-complète, on obtient l’estimation ponctuelle suivante: – est. valeur totale = -55 533 + 1, 816*65 000 + 49, 833*1 500 + 11 696*2 + 18 430*1 = 179 074$ – intervalle de confiance à 95% pour la moyenne de la valeur totale: [170 842, 187 306] – intervalle de confiance à 95% pour une valeur totale prédite : [116 173, 241 974] 38

Remarques: • Les longueurs des intervalles de confiance au niveau 95% du modèle de régression multiple pour une propriété de 1500 pi 2 sont plus petites que pour le modèle de régression simple. • Donc l’addition de plusieurs autres variables dans le modèle a aidé à expliquer encore plus la variabilité de la valeur totale et à améliorer nos estimations. • Si deux ou plusieurs variables indépendantes sont corrélées on dira qu’il y a multicolinéarité. Ceci peut influencer les valeurs des paramètres dans le modèle. • Aussi, si deux variables indépendantes sont fortement corrélées, alors seulement une des deux variables sera incluse dans le modèle, l ’autre n ’apportant que très peu d ’information supplémentaire. • Certaines conditions sont nécessaires à la validité du modèle et de l ’inférence correspondante (similaire à la régression linéaire simple). 39

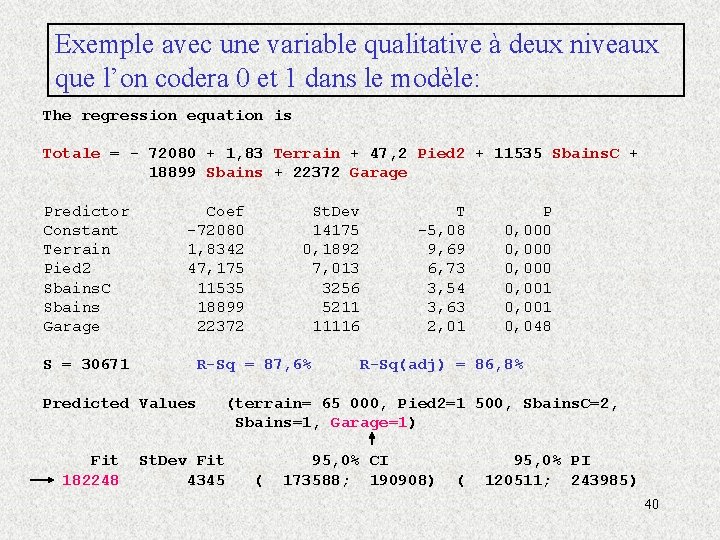
Exemple avec une variable qualitative à deux niveaux que l’on codera 0 et 1 dans le modèle: The regression equation is Totale = - 72080 + 1, 83 Terrain + 47, 2 Pied 2 + 11535 Sbains. C + 18899 Sbains + 22372 Garage Predictor Constant Terrain Pied 2 Sbains. C Sbains Garage Coef -72080 1, 8342 47, 175 11535 18899 22372 S = 30671 R-Sq = 87, 6% Predicted Values Fit 182248 St. Dev 14175 0, 1892 7, 013 3256 5211 11116 T -5, 08 9, 69 6, 73 3, 54 3, 63 2, 01 P 0, 000 0, 001 0, 048 R-Sq(adj) = 86, 8% (terrain= 65 000, Pied 2=1 500, Sbains. C=2, Sbains=1, Garage=1) St. Dev Fit 4345 ( 95, 0% CI 173588; 190908) ( 95, 0% PI 120511; 243985) 40

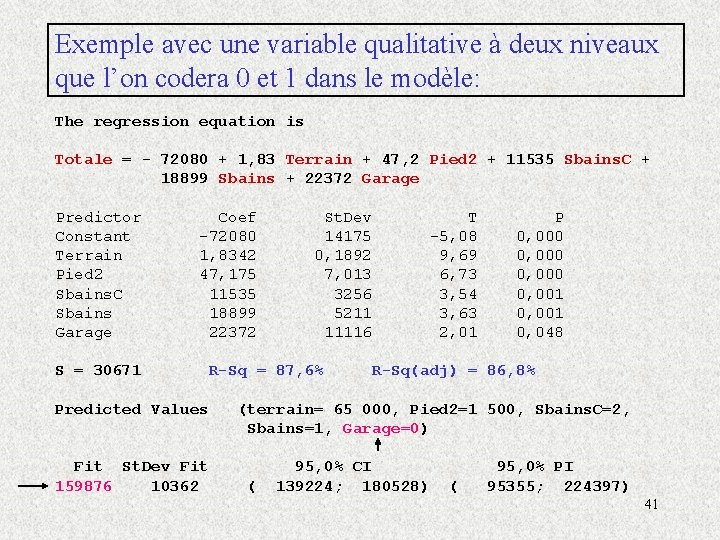
Exemple avec une variable qualitative à deux niveaux que l’on codera 0 et 1 dans le modèle: The regression equation is Totale = - 72080 + 1, 83 Terrain + 47, 2 Pied 2 + 11535 Sbains. C + 18899 Sbains + 22372 Garage Predictor Constant Terrain Pied 2 Sbains. C Sbains Garage Coef -72080 1, 8342 47, 175 11535 18899 22372 S = 30671 Predicted Values Fit St. Dev Fit 159876 10362 St. Dev 14175 0, 1892 7, 013 3256 5211 11116 R-Sq = 87, 6% T -5, 08 9, 69 6, 73 3, 54 3, 63 2, 01 P 0, 000 0, 001 0, 048 R-Sq(adj) = 86, 8% (terrain= 65 000, Pied 2=1 500, Sbains. C=2, Sbains=1, Garage=0) ( 95, 0% CI 139224; 180528) ( 95, 0% PI 95355; 224397) 41