La suite logistique et le chaos Daprs la

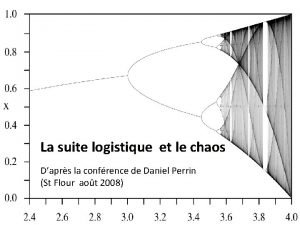
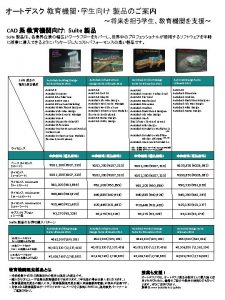
La suite logistique et le chaos D’après la conférence de Daniel Perrin (St Flour août 2008)

Modèles d’évolution de population Euler (1707 -1783), Malthus (1766 -1834) et Verhulst (1804 -1849) vont s’occuper successivement de créer des modèles d’évolution de populations: Euler, vers 1760 ( « Recherches générales sur la mortalité et la multiplication du genre humain » ), est conduit à déterminer la population d’une ville à une date donnée. Ses calculs reviennent à étudier une suite géométrique. Malthus reprend en 1798 l’idée d’un accroissement exponentiel de la population. Il modélise la population humaine comme une suite géométrique et la capacité de production comme une suite arithmétique. La distorsion entre les deux, le conduit à une proposition de limitation des naissances. Le modèle malthusien est remis en cause vers 1840 par Verhulst qui propose un modèle dit logistique qui prend en compte la limitation de la population. Le principe est simple : l’accroissement de la population n’est proportionnel à la population que pour les petites valeurs de celle-ci. Lorsqu’elle croît, des facteurs limitants apparaissent qui font qu’il y a une population maximale M. Verhulst postule alors que l’accroissement de la population x est proportionnel à la quantité x(M − x). Ce modèle lui permet de donner en 1837 une prévision de la population de la France en 1930 de 40 millions, alors qu’elle sera de 41, 5 millions en 1931. (ce modèle ne pouvait pourtant prévoir ni les guerres de 70 et 14, ni la commune, ni la grippe espagnole!).

Modèles d’évolution de population Modèles continus Le temps est continu, t R, et on a une fonction p(t) à valeurs réelles. Dans ce cas, on suppose que si on connaît la population au temps t, on la connaît au temps t + dt, avec dt infinitésimal. Cela revient à se donner la dérivée en fonction de p(t). On ne s’intéresse ici qu’aux cas où la population suit un modèle autonome au sens où elle ne dépend pas du temps. On aura donc une équation de la forme p’ = f(p), la fonction f étant indépendante du temps. 1) P’(t)=K. P(t). (Euler et Malthus) Solution : P(t) = P(0). ekt Pas raisonnable à terme: la population tend vers l’infini. 2) P’(t)= m. P(t). (M-P(t)) (Verhulst) : On borne la population par M. Solution : avec

Modèles d’évolution de population Modèles discret Le temps est discret, n N (n désigne un nombre de minutes, d’heures…) et on a une suite pn à valeurs réelles. Dans ce cas, on se donne l’accroissement pn+1 − pn en fonction de pn. Le modèle est toujours autonome. La suite peut représenter: • En génétique : la fréquence d’un gène au temps n. • En épidémiologie : la proportion de la population infectée au temps n. • En économie : n est la quantité de marchandises et pn le prix. • En sciences sociales, l’étude de la propagation des rumeurs. 1) Pn+1 – Pn = K. Pn (K>0) : Pn = (1+K)n P 0. Pas raisonnable : diverge vers l’infini. 2) Pn+1 = m. Pn - l. Pn² = m. Pn (1 - (l/m)Pn) est borné par m/l Si on pose Un = (l/m)Pn on obtient : Un+1 = m Un (1 -Un) (la suite logistique). Pour que Un [0 ; 1] il est nécessaire que m [0 ; 4] : f(x)= mx(1 -x) atteint son max sur [0; 1] pour x=1/2 et f(1/2)= m/4 qui doit appartenir à [0 ; 1]… L’étude de la suite U quand m [0 ; 4] est très compliquée et l’étude de la suite logistique U reste encore OUVERTE…

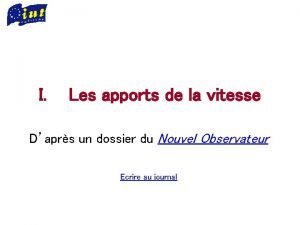
Etude de la suite logistique Points fixes de f (1 -cycle): cas m ]0 ; 3] Pour m [0 ; 1] : U est décroissante, convergente vers 0 Les points fixes de f sont les solutions de g 1(x) = f(x) - x = 0 ( où f(x) = mx(1 - x) ) Il y a 2 points fixes : 0 et t = 1 -1/m. Pour m ]1 ; 2] : U est monotone, convergente vers t Ils peuvent être attractifs ou répulsifs : Pour m ]2 ; 3] : U est en escargot, convergente vers t Le point fixe t est répulsif si ∣f’(t)∣>1 et attractif si ∣f’(t)∣ <1. Attractif: f’(t)= - 0, 4 On est ici t Pour m ]2 ; 3] : Pour m [0 ; 1] : Pour m ]1 ; 2] : 0 est attractif, 0 est répulsif, Cas m ]3 ; 4] : U est décroissante, t est attractif, 0 et t sont répulsifs… convergente vers 0 ; U est monotone, U est en « escargot » U diverge en général pas de t dans ]0 ; 1] U converge vers t. (à partir d’un certain rang) , (sauf si U 0=f(-k)(t) ou 0 ou 1) U converge vers t. Le problème est : De quelle façon cela diverge ? Vision sur géogébra m

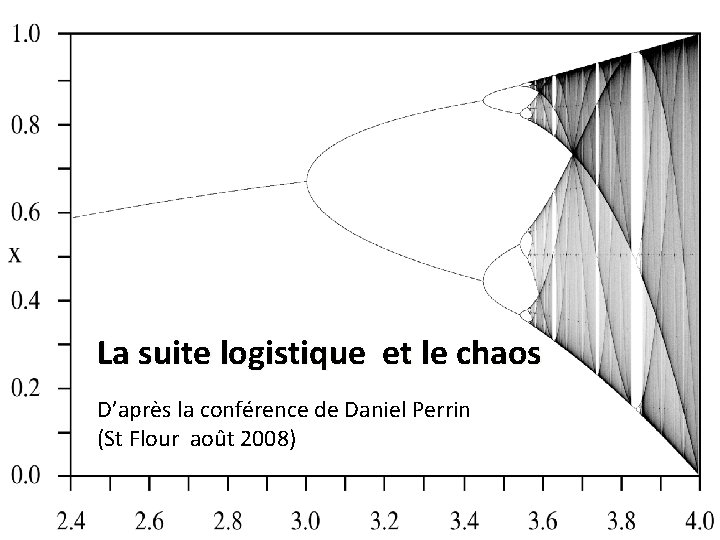
Etude de la suite logistique Points fixes de f 2 (2 -cycle): cas m ]3 ; m 2] Ce sont les points fixes de f 2 (=fof) qui ne sont pas des points fixes de f. Th de Coppel : Si f n’a pas de 2 -Cycle alors la suite converge… Il y a donc des 2 -cycles dans le cas où m ]3 ; 4]. Il s’agit de trouver les racines de g 2(x)=f(f(x))-x=0 qui ne sont pas 0 et t. Les solutions de f(f(x))=x sont les points fixes de f : 0 et t =1 -1/m, puis deux autres : a et b sont dans [0 ; 1] et on a : f(a)=b et f(b)=a Ce cycle est-il attractif ou répulsif ? Pour m= Le 2 -cycle est « super attractif » . m 2

Etude de la suite logistique Points fixes de f 2 (2 -cycle): cas m ]3 ; m 2] Vision sur géogébra

Etude de la suite logistique Pour m [0 ; 1] : U est décroissante, convergente vers 0 Pour m ]1 ; 2] : U est monotone, convergente vers t Pour m ]2 ; 3] : U est en escargot, convergente vers t Pour m ]3; m 2[ : U a deux points d’accumulation a et b Pour m ] 3; m 2[ : U 2 n converge vers a. U 2 n+1 converge vers b. m 2 = Pour m = Le cycle est super attractif On est ici b a m m 2

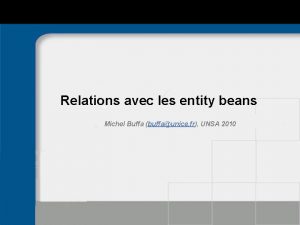
Points fixes de f 4 (4 -cycle): cas m ] m 2; m 3[ Lorsque le cycle d’ordre 2 cesse d’être attractif, le théorème de Coppel, appliqué à f², montre qu’il y a un cycle d’ordre 2 pour f², donc d’ordre 4 pour f. A partir de maintenant, on a à résoudre des équations algébriques de plus en plus compliquées (degré 16 pour f 4). Il s’agit de trouver les racines de g 4(x)=f(f(x))))-x=0 qui ne sont pas 0, a, b et t déjà trouvés. Etude de la suite logistique

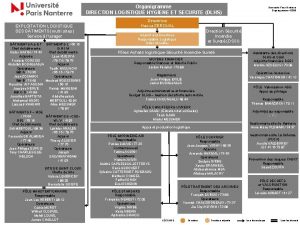
Points fixes de f 4 (4 -cycle): cas m ] m 2; m 3[ Etude de la suite logistique Ce 4 -cycles existe et est attractif pour m ] m 2 ; m 3 [ avec m 3 ≈ 3, 544 On ne connaît pas les valeurs exactes du 4 -cycle en fonction de m racines du polynôme suivant: Tout se fait numériquement pour un m donné. On connaît encore moins la valeur exacte de m 3: tout se fait numériquement, et c’est difficile! Vision sur géogébra

Pour m [0 ; 1] : U est décroissante, convergente vers 0 Pour m ]1 ; 2] : U est monotone, convergente vers t Pour m ]2 ; 3] : U est en escargot, convergente vers t Pour m ]3; m 2[ : U a 2 points d’accumulation a et b Pour m ] m 2; m 3[ : U a 4 points d’accumulation Etude de la suite logistique Pour m ] m 2; m 3[ : U 4 n converge vers a 1. U 4 n+1 converge vers a 2. U 4 n+2 converge vers a 3. U 4 n+3 converge vers a 4. m 2 ≈ 3, 449490 m 3 ≈ 3, 544090 On est ici m Pour m ≈ 3, 49856 Le cycle est super attractif m 2 m 3

Les 4 -cycle, 8 -cycles …: cas m ] m 3; m [ Etude de la suite logistique Lorsque le cycle d’ordre 4 cesse d’être attractif, le théorème de Coppel, appliqué à f 4, montre qu’il y a un cycle d’ordre 2 pour f 4, donc d’ordre 8 pour f etc. On aura donc des 8 -cycles, 16 cycles … 2 n-cycles, attractifs sur ] m 3; m 4[, ] m 4; m 5[, … ] mn; mn +1[ Par des algorithmes complexes, on trouve: m 4 ≈ 3, 564407… et m ≈ 3, 5699456. Calcul des cycles sur Excel:

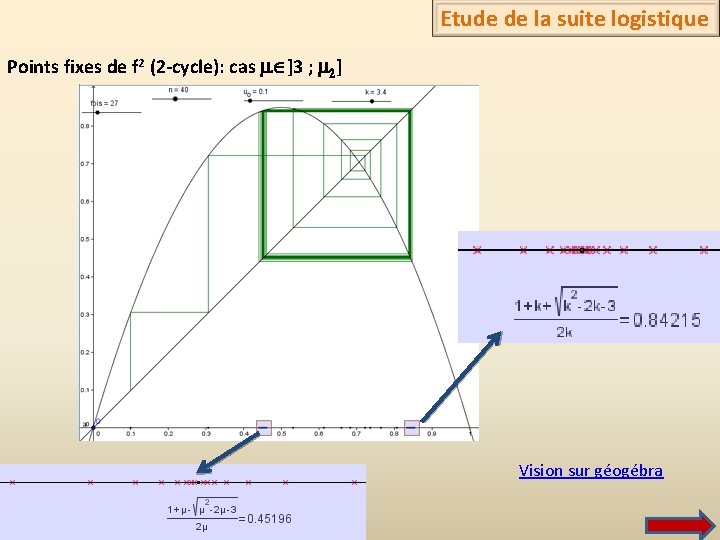
En résumé sur [0; m [: Etude de la suite logistique Pour m [0 ; 1] : U est décroissante, convergente vers 0 Pour m ]1 ; 2] : U est monotone, convergente vers t Pour m ]2 ; 3] : U est en escargot, convergente vers t Pour m ]3; m 2[ : U a 2 points d’accumulation Pour m ] m 2; m 3[ : U a 4 points d’accumulation… Pour m ] mn; mn +1[ : U a 2 n points d’accumulation… m 1 = 3 m 2 ≈ 3, 449490 m 3 ≈ 3, 544090 m 4 ≈ 3, 564407 …. m ≈ 3, 5699456 Visualisation d’un 8 -cycle sur géogébra m

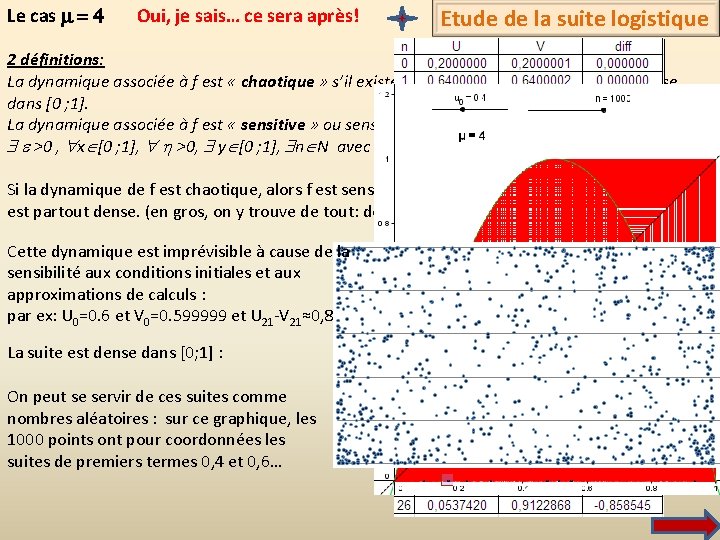
Le cas m = 4 Oui, je sais… ce sera après! Etude de la suite logistique 2 définitions: La dynamique associée à f est « chaotique » s’il existe U 0 tel que la suite U est partout dense dans [0 ; 1]. La dynamique associée à f est « sensitive » ou sensible aux conditions initiales, si : e >0 , x [0 ; 1], h >0, y [0 ; 1], n N avec ∣ x - y∣ < h et ∣ f n (x)- f n (y)∣ > e (pffff!!!) Si la dynamique de f est chaotique, alors f est sensitive et l’ensemble des points périodiques de f est partout dense. (en gros, on y trouve de tout: des 3 -cycles, des 4 cycles , des 5 cycles…) Cette dynamique est imprévisible à cause de la sensibilité aux conditions initiales et aux approximations de calculs : par ex: U 0=0. 6 et V 0=0. 599999 et U 21 -V 21≈0, 8 La suite est dense dans [0; 1] : On peut se servir de ces suites comme nombres aléatoires : sur ce graphique, les 1000 points ont pour coordonnées les suites de premiers termes 0, 4 et 0, 6…

Le cas m = 4 Etude de la suite logistique Des points particuliers En remarquant que (dans le cas m=4), f(sin²( q))=sin(2 q), on obtient avec U 0 = sin²(q): Un=sin²(2 n q) Avec avec 0 k <2 p-1 ou avec 0 k 2 p-1 , La suite U est périodique de période p (sauf si peut se simplifier en avec 0<k’<k et 0<p’<p) Par exemple: : U est de période 4. Ou encore : U est de période 3. En revanche les erreurs d’approximations des logiciels font que les suites n’apparaissent pas cycliques… Visualisation sur géogébra de ces cas

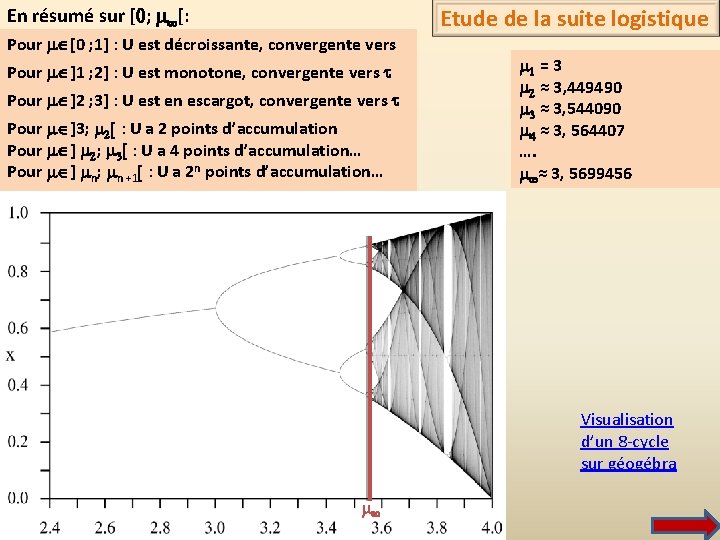
Le cas très difficile m ] m ; 4[ Etude de la suite logistique Il y a donc deux 3 -cycle pour m=3, 831: Le théorème de «Sarkovsky » (forme faible (!!!), très faible ce Sarkovsky) : {0. 1550726466 , 0. 5019572381 , 0. 9577353243 } très attractif Si f admet un point de période 3, alors f admet des points périodique de toutes les périodes n>0. Et {0. 1645585343 , 0. 5266821375 , 0. 9550225714} lentement répulsif et aussi : La fonction f admet des points de période 3 pour (et donc de toutes les périodes). Le reste: et plein d’autres trucs incompréhensibles !!! (pour moi évidemment) Cherchons donc un de ces fameux 3 -cycles pour m=3, 831 , avec Xcas: Je ne comprends RIEN….

Utilisation en classe Etude de la suite logistique En 2003, nous recevions la base d’exercices de bac (en vue du nouveau bac). Il y avait ce problème de coccinelles: On y étudiait donc la suite logistique dans différent cas: k=1 (cv vers 0) puis k=1, 8 (cv vers t) et enfin k=3, 2 (2 -cycle). . L’idée m’est venue de reprendre ce classique pour un td en 1ère S avec l’objectif de représenter des suites avec la calculatrice. Le début de l’énoncé étant similaire à ce qui précède, voici les questions:

Bibliographie Pour l’essentiel, le document de Daniel Perrin dont j’ai tenté de restituer à peine le centième! http: //www. math. u-psud. fr/~perrin/Conferences/logistique. DP. pdf Le Wiki: http: //fr. wikipedia. org/wiki/Suite_logistique Les différents fichiers géogébra et le diaporama sont en ligne sur mon site: http: //bretin. jacques. free. fr ET Voilà !!