Prof dr sc Pavao Marovi Otpornost materijala I

Prof. dr. sc. Pavao Marović Otpornost materijala I Šk. god. 2008/2009 Otpornost materijala I 0, 1, 2, 3, 4, 5, 6, 7, nastavak 8. 1

8. SAVIJANJE RAVNIH ŠTAPOVA Pravo Čisto Koso Sa silama Promatramo ravni štap, napravljen od homogenog, izotropnog, elastičnog materijala, konstantnog poprečnog presjeka, koji je opterećen konstantnim momentom savijanja. Prema tome, svaki dio štapa se nalazi u jednakim uvjetima. Za jedan diferencijalni dio štapa napravit ćemo sve analize. Otpornost materijala I 8. Savijanje 2

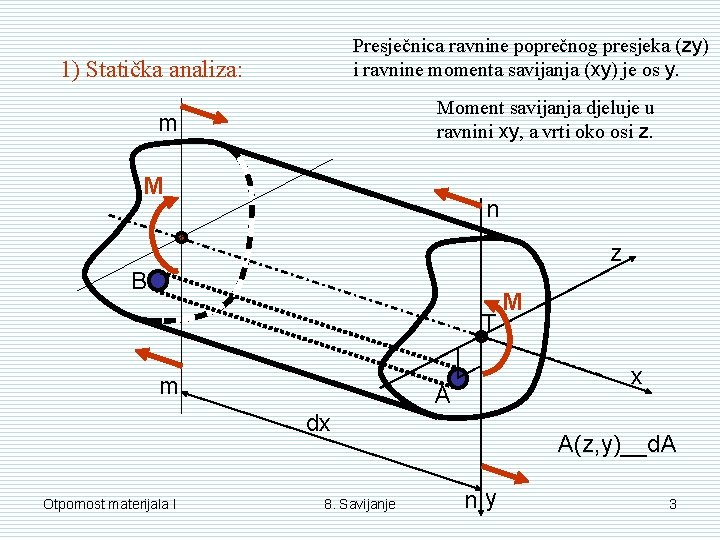
Presječnica ravnine poprečnog presjeka (zy) i ravnine momenta savijanja (xy) je os y. 1) Statička analiza: Moment savijanja djeluje u ravnini xy, a vrti oko osi z. m M n z B T m x A dx Otpornost materijala I 8. Savijanje M A(z, y)__d. A ny 3

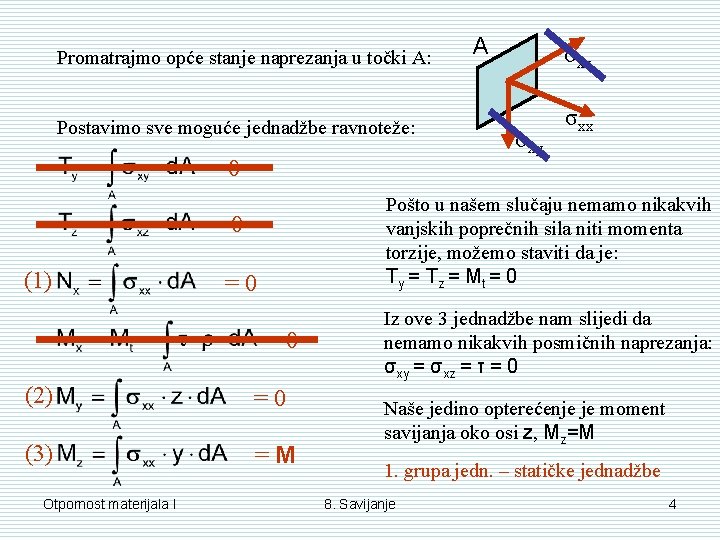
Promatrajmo opće stanje naprezanja u točki A: Postavimo sve moguće jednadžbe ravnoteže: =0 =0 =0 (2) =0 (3) =M Otpornost materijala I σxz σxy σxx Pošto u našem slučaju nemamo nikakvih vanjskih poprečnih sila niti momenta torzije, možemo staviti da je: T y = T z = Mt = 0 =0 (1) A Iz ove 3 jednadžbe nam slijedi da nemamo nikakvih posmičnih naprezanja: σxy = σxz = τ = 0 Naše jedino opterećenje je moment savijanja oko osi z, Mz=M 1. grupa jedn. – statičke jednadžbe 8. Savijanje 4

2) Geometrijska analiza: Da bi odredili zakon razdiobe normalnih naprezanja po visini poprečnog presjeka, promatrati ćemo ponašanje vlakanaca na diferencijalnom elementu dx. Uzeti ćemo neopterećeni štap i na njemu nacrtati dva sustava međusobno okomitih linija: (1) konture poprečnih presjeka; i (2) paralelne izvodnice (slika 14. 7, str. 309). a a 1<a neutralni sloj a 2>a Otpornost materijala I 8. Savijanje Nakon što smo štap opteretili momentom savijanja, štap će se deformirati: (1) poprečni presjeci će ostati ravni i okomiti na uzdužnu os (Navier-ova pretpostavka o ravnim presjecima), zaokrenuti i radijalno usmjereni te okomiti na uzdužne izvodnice; (2) izvodnice će činiti sustav koncentričnih kružnica. Što se dogodilo s izvodnicama? - neke su se skratile, a 1<a - neke su se produljile, a 2>a - neke su ostale nepromijenjene 5

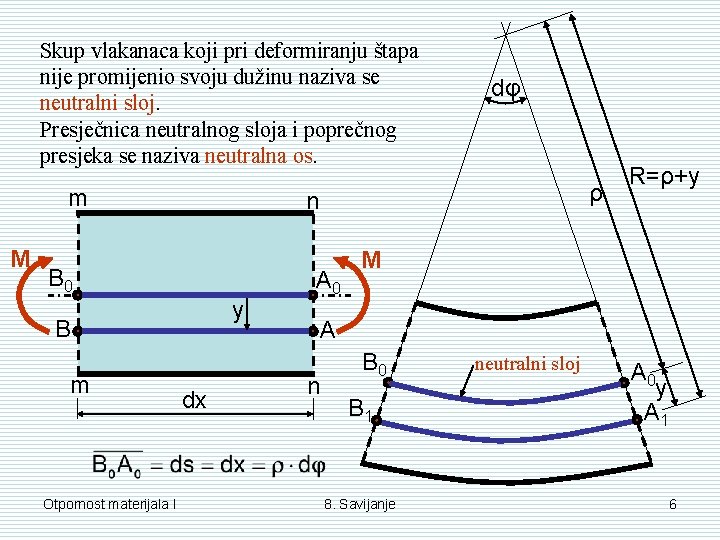
Skup vlakanaca koji pri deformiranju štapa nije promijenio svoju dužinu naziva se neutralni sloj. Presječnica neutralnog sloja i poprečnog presjeka se naziva neutralna os. m M y B Otpornost materijala I ρ n B 0 m dφ dx A 0 R=ρ+y M A n B 0 B 1 8. Savijanje neutralni sloj A 0 y A 1 6

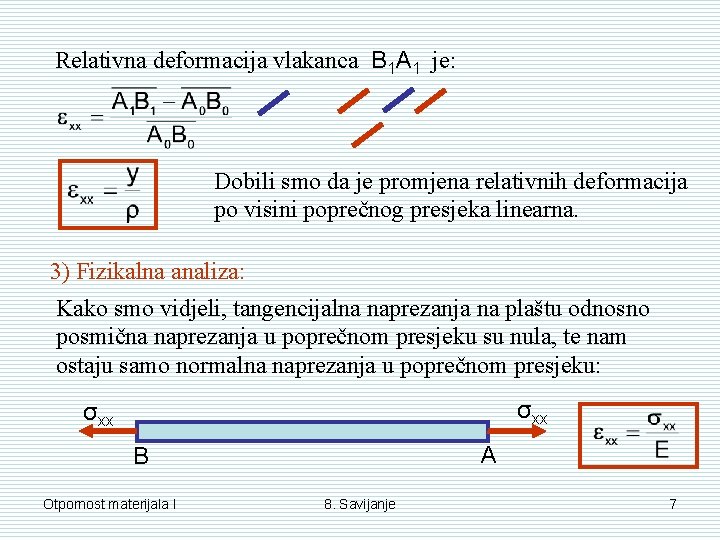
Relativna deformacija vlakanca B 1 A 1 je: Dobili smo da je promjena relativnih deformacija po visini poprečnog presjeka linearna. 3) Fizikalna analiza: Kako smo vidjeli, tangencijalna naprezanja na plaštu odnosno posmična naprezanja u poprečnom presjeku su nula, te nam ostaju samo normalna naprezanja u poprečnom presjeku: σxx A B Otpornost materijala I 8. Savijanje 7

4) Rješavanje sustava jednadžbi: Vidimo da je raspodjela normalnih naprezanja po visini poprečnog presjeka linearna. Iz jednadžbe (3): slijedi: Kako je E konstantno, ako se radi o homogenom i izotropnom materijalu, možemo pisati: Ako uzmemo da je [m 4] osni moment tromosti ili mom. trom. obzirom na os z Izraz za deformaciju kod savijanja: Pri tome je E·Iz – krutost na savijanje ili savojna krutost. Otpornost materijala I 8. Savijanje 8

Ako izraz za deformaciju uvrstimo u izraz za opću raspodjelu normalnih naprezanja po visini poprečnog presjeka dobiti ćemo izraz koji nam daje mogućnost određivanja normalnih naprezanja pri istom savijanju u bilo kojoj točki presjeka: Promatrajmo jednadžbu (1): Kako je slijedi da je Sz - statički moment površine obzirom na os z [m 3] Ovo je ujedno jednadžba težišta poprečnog presjeka, a pokazuje da neutralna os prolazi težištem poprečnog presjeka. Otpornost materijala I 8. Savijanje 9

Preostaje nam još jednadžba (2): Kako je slijedi da je Izy - centrifugalni moment tromosti u odnosu na osi z i y [m 4] Prema tome, da bi sve ovo što smo do sada kazali bilo ispravno, centrifugalni moment tromosti obzirom na osi z i y mora biti jednak nuli, odnosno, ravnina djelovanja momenta savijanja mora biti ili ravnina xy (što je ovdje pokazano) ili ravnina xz (slično uz zamjenu indeksa). Otpornost materijala I 8. Savijanje 10

Komentari: Os x se podudara s osi štapa. Os y prolazi težištem poprečnog presjeka – Sy=0. Os z prolazi težištem poprečnog presjeka – Sz=0. Osi y i z su središnje osi poprečnog presjeka, može ih biti više. Ravnina djelovanja momenta savijanja prolazi kroz os štapa. Centrifugalni moment tromosti Izy=0 → osi y i z su glavne osi poprečnog presjeka, ima samo jedan par. Sz=Sy=0 → osi z i y su središnje osi Izy=0 → osi z i y su glavne osi Sz=Sy=Izy=0 → osi z i y su glavne središnje osi Za slučaj pravog čistog savijanja, ravnina djelovanja momenta savijanja mora se poklapati s jednom od ravnina glavnih osi, xy ili xz. Otpornost materijala I 8. Savijanje 11

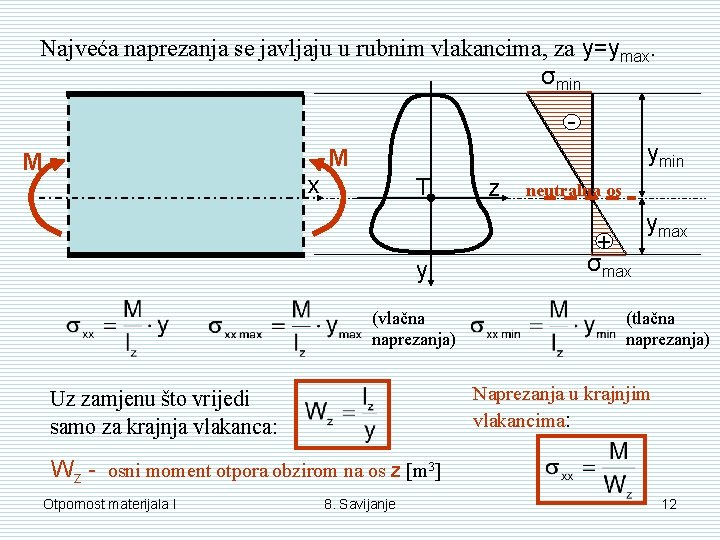
Najveća naprezanja se javljaju u rubnim vlakancima, za y=ymax. σmin ymin M M x T y (vlačna naprezanja) z neutralna os + σmax ymax (tlačna naprezanja) Naprezanja u krajnjim vlakancima: Uz zamjenu što vrijedi samo za krajnja vlakanca: Wz - osni moment otpora obzirom na os z [m 3] Otpornost materijala I 8. Savijanje 12

Za prethodni poprečni presjek u rubnim vlakancima imamo: Za poprečni presjek simetričan obzirom na os z, ymax = ymin = h/2: Uvjet čvrstoće moramo ispuniti na oba ruba, σvlak ≠ σtlak : Otpornost materijala I 8. Savijanje 13

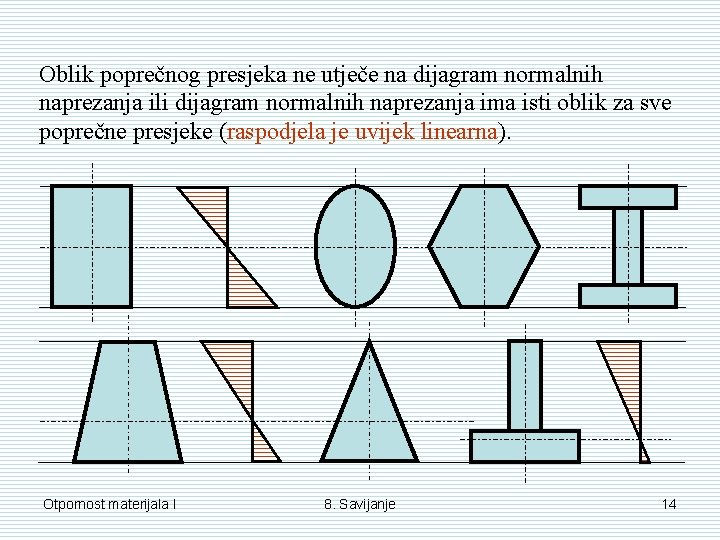
Oblik poprečnog presjeka ne utječe na dijagram normalnih naprezanja ili dijagram normalnih naprezanja ima isti oblik za sve poprečne presjeke (raspodjela je uvijek linearna). Otpornost materijala I 8. Savijanje 14

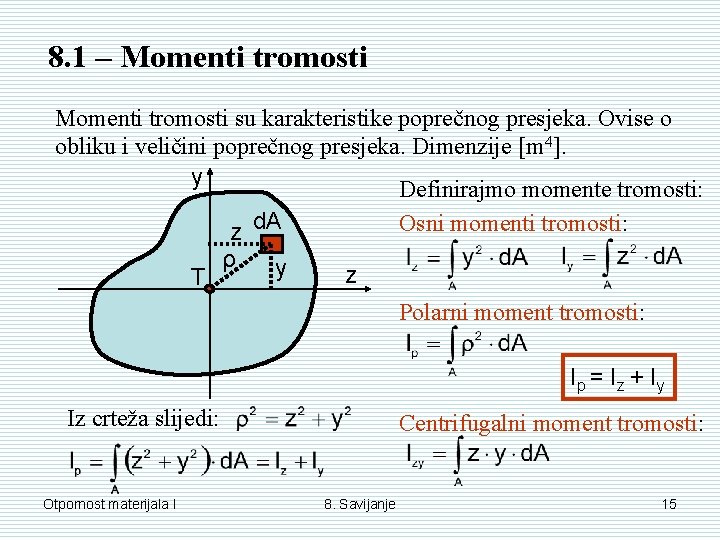
8. 1 – Momenti tromosti su karakteristike poprečnog presjeka. Ovise o obliku i veličini poprečnog presjeka. Dimenzije [m 4]. y Definirajmo momente tromosti: z d. A ρ y T Osni momenti tromosti: z Polarni moment tromosti: Ip = I z + Iy Iz crteža slijedi: Otpornost materijala I Centrifugalni moment tromosti: 8. Savijanje 15

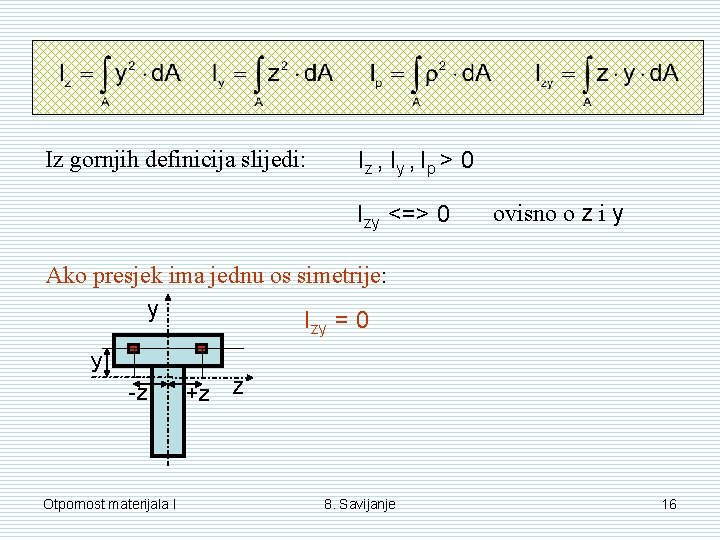
Iz gornjih definicija slijedi: Iz , Iy , Ip > 0 Izy <=> 0 ovisno o z i y Ako presjek ima jednu os simetrije: y I =0 zy y -z Otpornost materijala I +z z 8. Savijanje 16

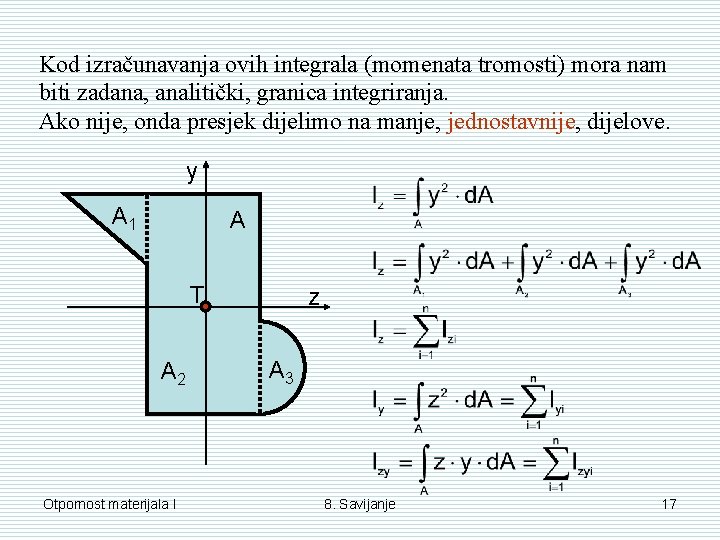
Kod izračunavanja ovih integrala (momenata tromosti) mora nam biti zadana, analitički, granica integriranja. Ako nije, onda presjek dijelimo na manje, jednostavnije, dijelove. y A 1 A T A 2 Otpornost materijala I z A 3 8. Savijanje 17

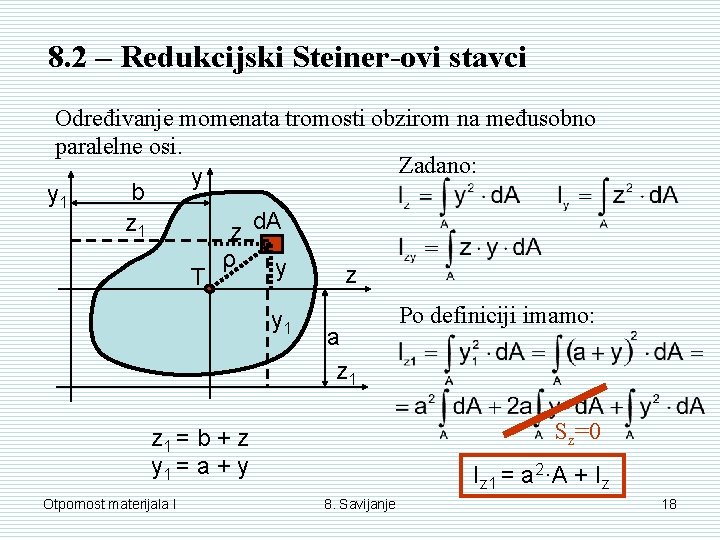
8. 2 – Redukcijski Steiner-ovi stavci Određivanje momenata tromosti obzirom na međusobno paralelne osi. Zadano: y b y 1 z d. A T ρ y y 1 z a z 1 Sz=0 z 1 = b + z y 1 = a + y Otpornost materijala I Po definiciji imamo: Iz 1 = a 2·A + Iz 8. Savijanje 18

Iz 1 = Iz + a 2·A Iy 1 = Iy + b 2·A Osni moment tromosti obzirom na neku zadanu os (z 1 ili y 1) jednak je momentu tromosti obzirom na paralelnu os (z ili y) kroz težište poprečnog presjeka plus produkt površine poprečnog presjeka (A) i kvadrata udaljenosti između paralelnih osi (a 2 ili b 2). Otpornost materijala I 8. Savijanje 19

Sy=0 Sz=0 Iz 1 y 1 = Izy + a·b·A Centrifugalni moment tromosti obzirom na zadani par međusobno okomitih osi (z 1, y 1) jednak je centrifugalnom momentu tromosti obzirom na sustav međusobno okomitih osi (z, y) kroz težište poprečnog presjeka koje su paralelne zadanim osima plus produkt površine poprečnog presjeka (A) i udaljenosti međusobno paralelnih osi (a, b). Otpornost materijala I 8. Savijanje 20

Zaključci / Komentari: Kod proračuna osnih momenata tromosti, udaljenosti dolaze na kvadrat (a 2, b 2) pa ne moramo voditi računa o predznacima tih dužina. Kod proračuna centrifugalnog momenta tromosti moramo voditi računa o predznacima dužina a i b jer ne dolaze pod kvadrat. Naime, dužine a i b su koordinate težišta poprečnog presjeka u koordinatnom sustavu z 1 -y 1. Osni momenti tromosti imaju najmanju vrijednost za osi koje prolaze kroz težište poprečnog presjeka (Iz<Iz 1, Iy<Iy 1). Otpornost materijala I 8. Savijanje 21

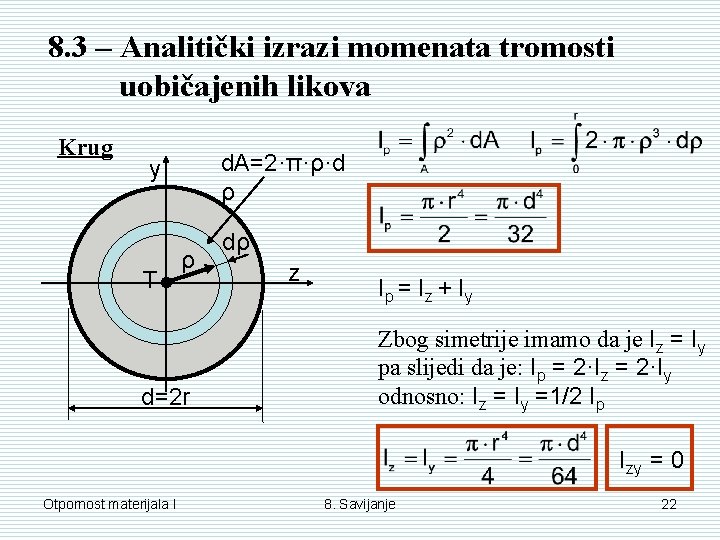
8. 3 – Analitički izrazi momenata tromosti uobičajenih likova Krug d. A=2·π·ρ·d ρ y T ρ d=2 r dρ z Ip = I z + Iy Zbog simetrije imamo da je Iz = Iy pa slijedi da je: Ip = 2·Iz = 2·Iy odnosno: Iz = Iy =1/2 Ip Izy = 0 Otpornost materijala I 8. Savijanje 22

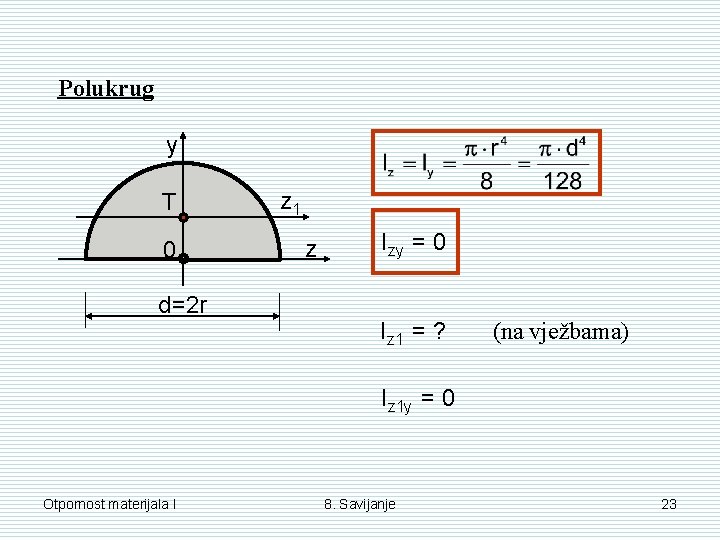
Polukrug y T 0 d=2 r z 1 z Izy = 0 Iz 1 = ? (na vježbama) Iz 1 y = 0 Otpornost materijala I 8. Savijanje 23

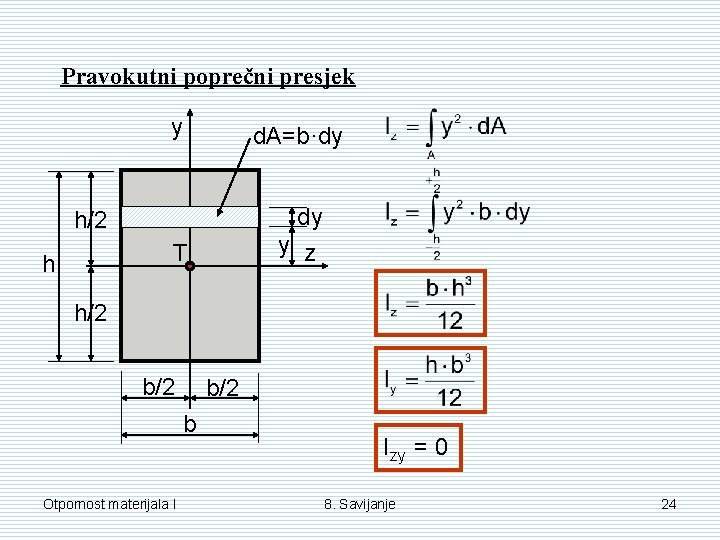
Pravokutni poprečni presjek y d. A=b·dy T dy y z h/2 h h/2 b/2 b Otpornost materijala I Izy = 0 8. Savijanje 24

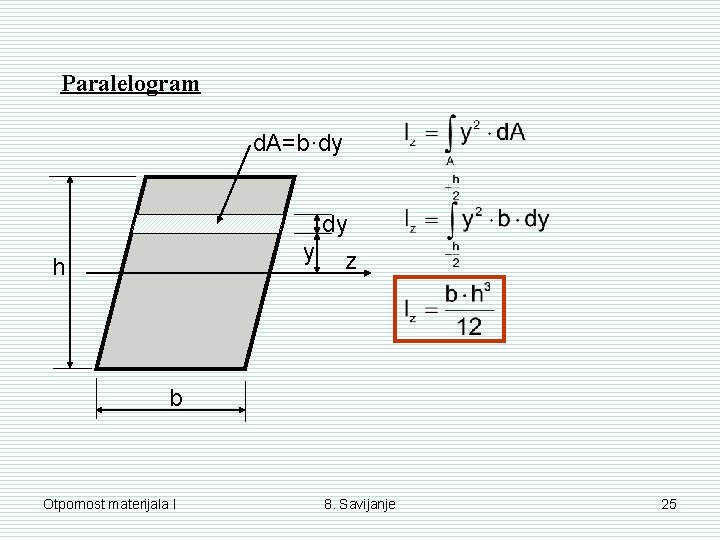
Paralelogram d. A=b·dy dy y h z b Otpornost materijala I 8. Savijanje 25

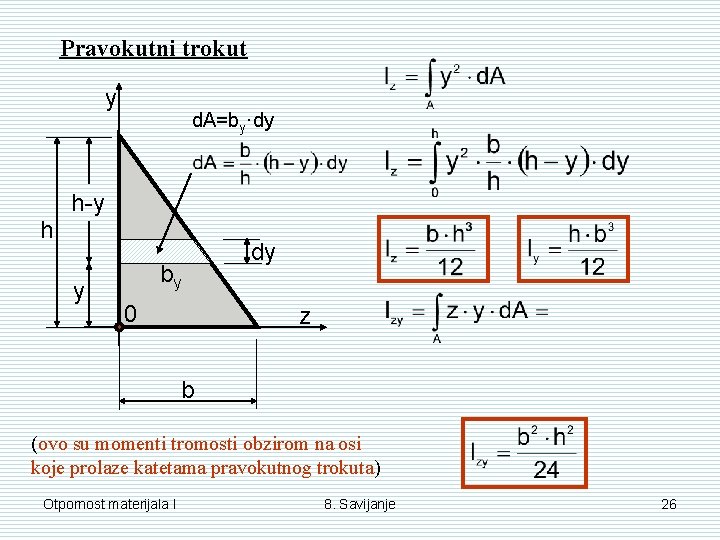
Pravokutni trokut y d. A=by·dy h-y h y by 0 dy z b (ovo su momenti tromosti obzirom na osi koje prolaze katetama pravokutnog trokuta) Otpornost materijala I 8. Savijanje 26

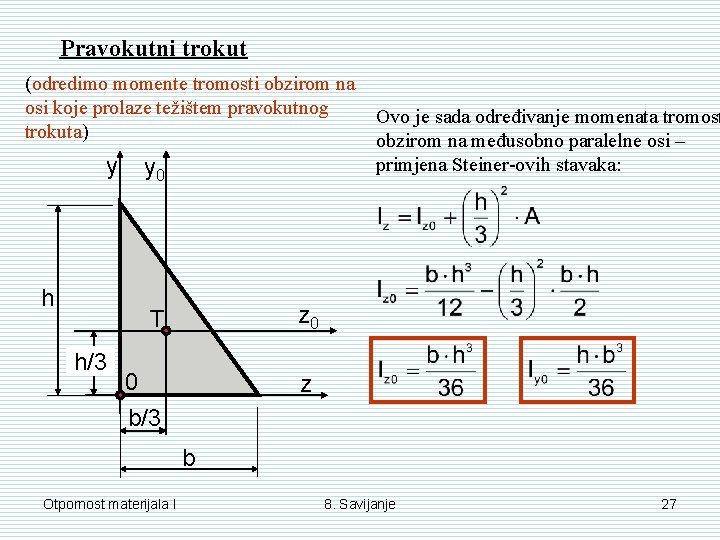
Pravokutni trokut (odredimo momente tromosti obzirom na osi koje prolaze težištem pravokutnog trokuta) y y 0 h z 0 T h/3 Ovo je sada određivanje momenata tromost obzirom na međusobno paralelne osi – primjena Steiner-ovih stavaka: 0 z b/3 b Otpornost materijala I 8. Savijanje 27

y h y 0 z 0 T h/3 + 0 z b/3 b T y 0 Otpornost materijala I 8. Savijanje z 0 28

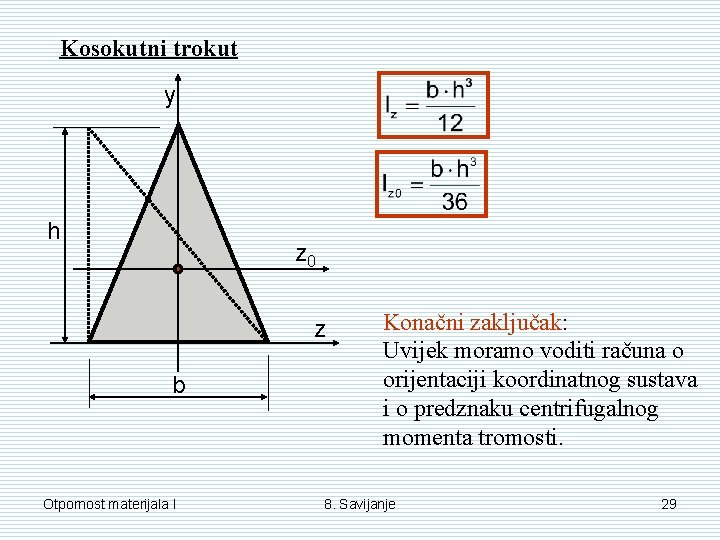
Kosokutni trokut y h z 0 z b Otpornost materijala I Konačni zaključak: Uvijek moramo voditi računa o orijentaciji koordinatnog sustava i o predznaku centrifugalnog momenta tromosti. 8. Savijanje 29

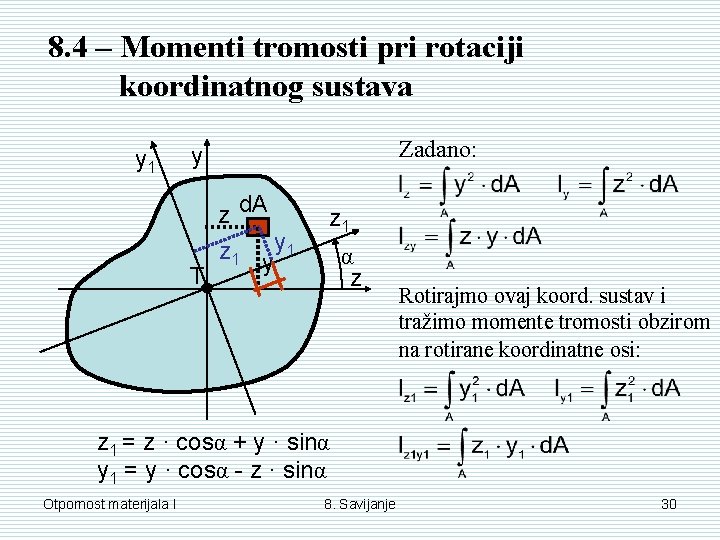
8. 4 – Momenti tromosti pri rotaciji koordinatnog sustava y 1 Zadano: y T z d. A z 1 y z 1 α z Rotirajmo ovaj koord. sustav i tražimo momente tromosti obzirom na rotirane koordinatne osi: z 1 = z · cosα + y · sinα y 1 = y · cosα - z · sinα Otpornost materijala I 8. Savijanje 30

Iz Iy Izy (1) Iy Iz (2) Otpornost materijala I 8. Savijanje 31

Izy Iz Iy Izy (3) Otpornost materijala I 8. Savijanje 32

(1) (2) Zbrojimo li jednadžbe (1) i (2), dobivamo: Iz 1 + Iy 1 = Iz + Iy = Ip - Invarijanta momenata tromosti Zbroj osnih momenata tromosti pri rotaciji koordinatnog sustava je konstantan i jednak polarnom momentu tromosti obzirom na pol rotacije. Otpornost materijala I 8. Savijanje 33

Pri rotaciji koordinatnog sustava osni momenti tromosti će u jednom trenutku poprimiti neke ekstremne vrijednosti ovisno o položaju koordinatnog sustava, tj. ovisno o kutu α. Da bi odredili te ekstreme trebamo derivirati jedn. (1) i (2) po α: Otpornost materijala I 8. Savijanje 34

Vidimo da nam derivacije osnih momenata tromosti po kutu α daju dvostruki centrifugalni moment tromosti s predznacima + i -. Za dobiti ekstremne vrijednosti, prve derivacije trebaju biti jednake nuli: Iz 1 y 1 = 0 Ekstremne vrijednosti osnih momenta tromosti nazivamo glavnim momentima tromosti a odgovarajuće osi, glavne osi tromosti. Ako glavne osi tromosti prolaze težištem poprečnog presjeka onda se zovu glavne središnje osi tromosti, a pripadajući momenti tromosti se zovu glavni središnji momenti tromosti. Otpornost materijala I 8. Savijanje 35

Glavne momente tromosti označavamo s Iu i Iv , a glavne osi tromosti s u i v. Smjer glavnih središnjih osi tromosti odredit ćemo prema jedn. (3): Iz prethodnog izraza dobijemo vrijednost za kut α 0 nakon čega veličine glavnih momenata tromosti nađemo tako da u jednadžbe (1) i (2) uvrstimo za kut α = α 0. Pošto je tangens periodična funkcija, perioda π/2, to ćemo za kut dobiti dvije vrijednosti – uzimamo manju vrijednost kuta |α 0|≤π/4 – u daljnjim razmatranjima uzimati ćemo samo ovu vrijednosti – kut α nanosimo po algebarskoj vrijednosti. y v u +α z Otpornost materijala I 8. Savijanje 36

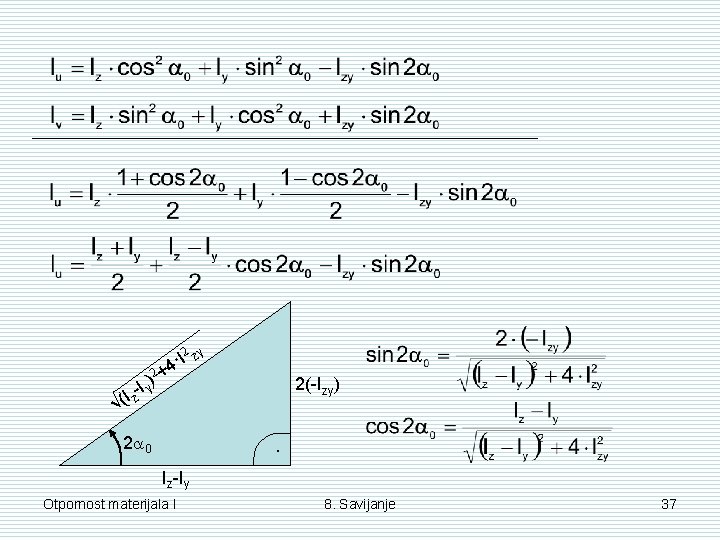
2 zy (I z √ ·I 4 )2 + 2(-Izy) Iy 2 0 · Iz-Iy Otpornost materijala I 8. Savijanje 37

Pošto je prvi član uvijek pozitivan, slijedi: Neke napomene: Ukoliko je Iz>Iy onda je Iu>Iv → Iu=Imax i Iv=Imin Ukoliko je Iz<Iy onda je Iu<Iv → Iv=Imax i Iu=Imin Ako presjek ima neku os simetrije onda je centrifugalni moment tromosti za tu os jednak nuli, pa je ta os ujedno i glavna os, a ako ima dvije osi onda će one same biti glavne osi. Otpornost materijala I 8. Savijanje 38

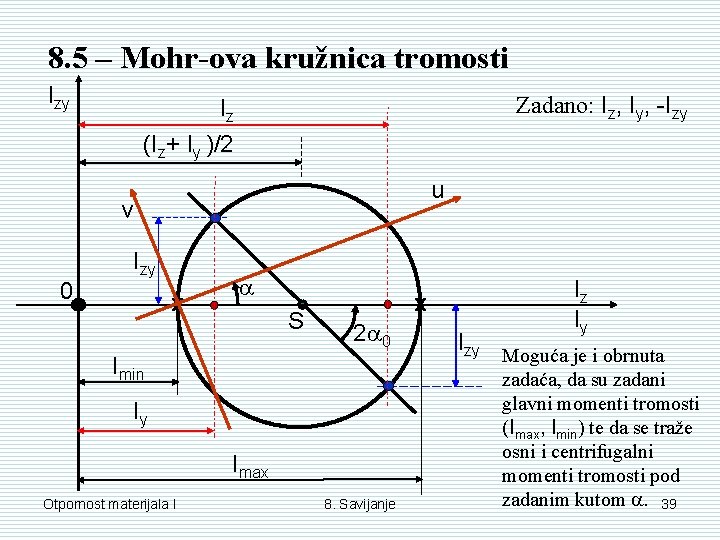
8. 5 – Mohr-ova kružnica tromosti Izy Zadano: Iz, Iy, -Izy Iz (Iz+ Iy )/2 u v 0 Izy x S x 2 0 Imin Iy Imax Otpornost materijala I 8. Savijanje Iz Iy Izy Moguća je i obrnuta zadaća, da su zadani glavni momenti tromosti (Imax, Imin) te da se traže osni i centrifugalni momenti tromosti pod zadanim kutom . 39

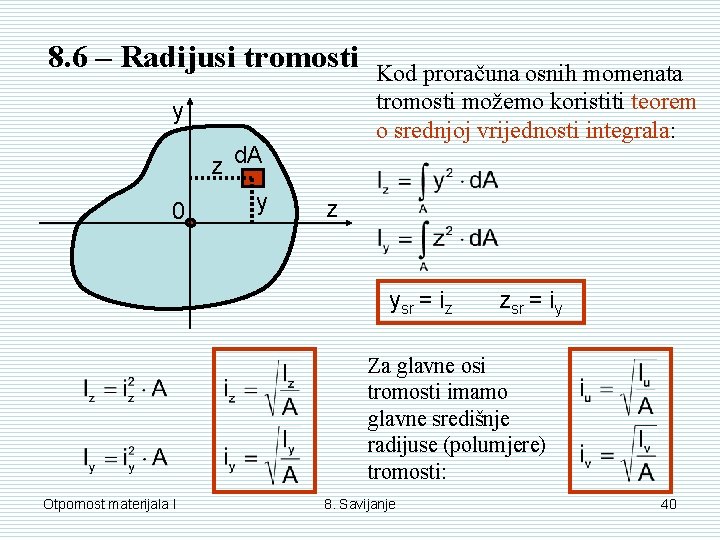
8. 6 – Radijusi tromosti y 0 z d. A y Kod proračuna osnih momenata tromosti možemo koristiti teorem o srednjoj vrijednosti integrala: z ysr = iz zsr = iy Za glavne osi tromosti imamo glavne središnje radijuse (polumjere) tromosti: Otpornost materijala I 8. Savijanje 40

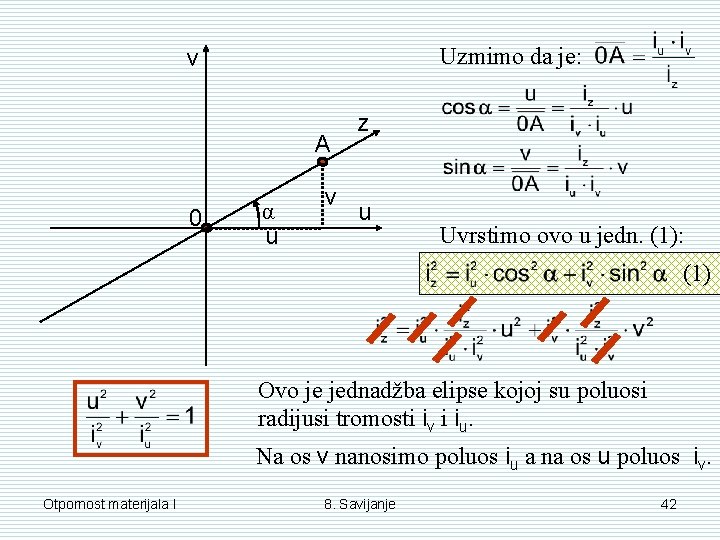
8. 7 – Elipsa tromosti Zadan je poprečni presjek s glavnim središnjim osima, Iuv=0. Neka je zadana i neka os z te se traži moment tromosti obzirom na tu os. v I =? z z 0 α u (1) Jednadžba (1) predstavlja jednadžbu elipse u u-v koordinatnom sustavu. Otpornost materijala I 8. Savijanje 41

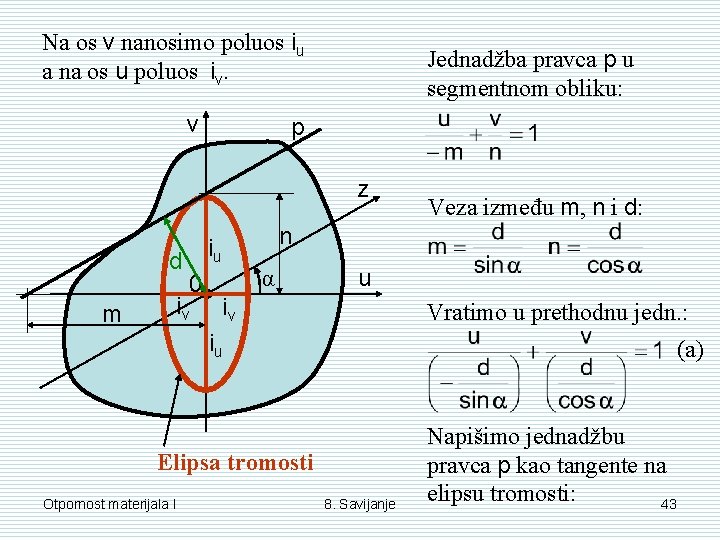
Uzmimo da je: v A 0 α u v z u Uvrstimo ovo u jedn. (1): (1) Ovo je jednadžba elipse kojoj su poluosi radijusi tromosti iv i iu. Na os v nanosimo poluos iu a na os u poluos iv. Otpornost materijala I 8. Savijanje 42

Na os v nanosimo poluos iu a na os u poluos iv. v Jednadžba pravca p u segmentnom obliku: p z d m n iu 0 iv Veza između m, n i d: α u iv Vratimo u prethodnu jedn. : iu (a) Elipsa tromosti Otpornost materijala I 8. Savijanje Napišimo jednadžbu pravca p kao tangente na elipsu tromosti: 43

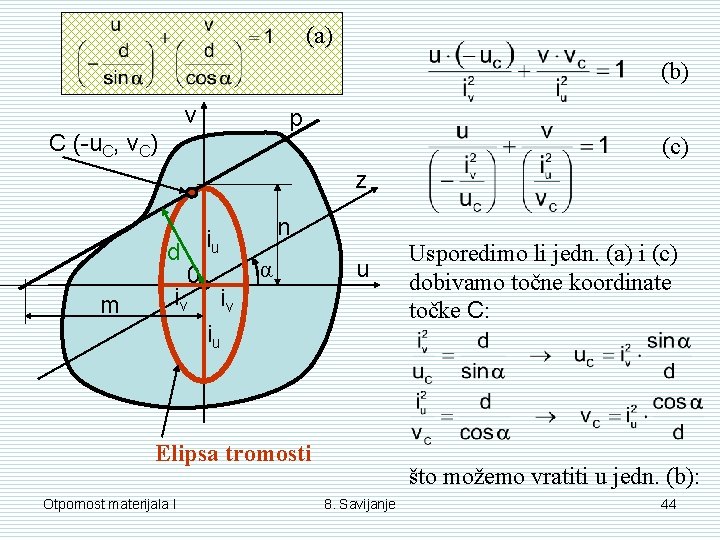
(a) (b) v p C (-u. C, v. C) (c) z d m n iu 0 iv α u iv iu Elipsa tromosti Otpornost materijala I Usporedimo li jedn. (a) i (c) dobivamo točne koordinate točke C: što možemo vratiti u jedn. (b): 8. Savijanje 44

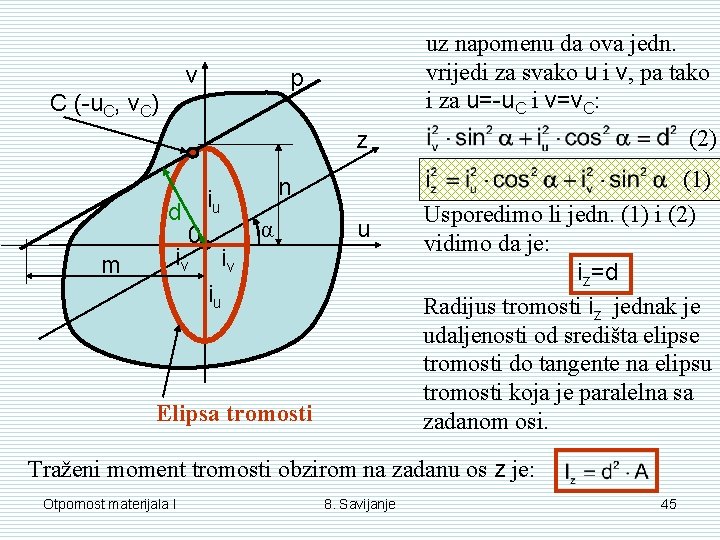
v uz napomenu da ova jedn. vrijedi za svako u i v, pa tako i za u=-u. C i v=v. C: p C (-u. C, v. C) (2) z d m n iu 0 iv α u iv iu Elipsa tromosti (1) Usporedimo li jedn. (1) i (2) vidimo da je: iz=d Radijus tromosti iz jednak je udaljenosti od središta elipse tromosti do tangente na elipsu tromosti koja je paralelna sa zadanom osi. Traženi moment tromosti obzirom na zadanu os z je: Otpornost materijala I 8. Savijanje 45

v p C (-u. C, v. C) odnosno: z d m n iu 0 iv α iv iu u z 1 a Slično se određuje moment tromosti i za os koja ne prolazi težištem poprečnog presjeka – os z 1: Elipsa tromosti Otpornost materijala I 8. Savijanje 46

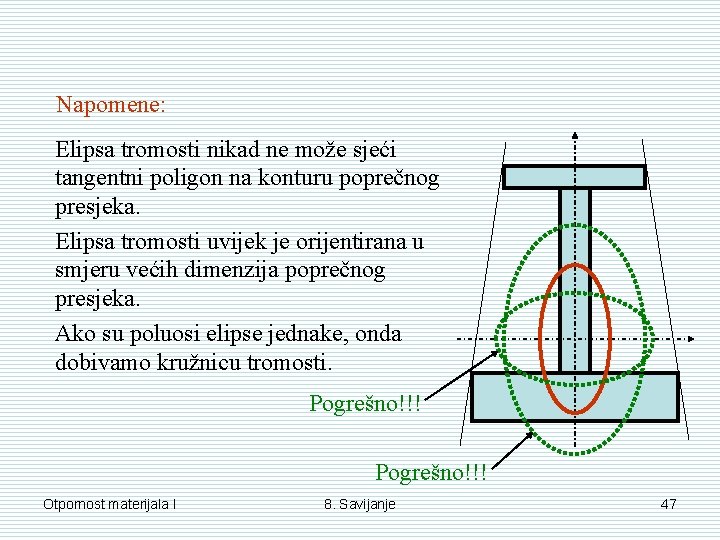
Napomene: Elipsa tromosti nikad ne može sjeći tangentni poligon na konturu poprečnog presjeka. Elipsa tromosti uvijek je orijentirana u smjeru većih dimenzija poprečnog presjeka. Ako su poluosi elipse jednake, onda dobivamo kružnicu tromosti. Pogrešno!!! Otpornost materijala I 8. Savijanje 47

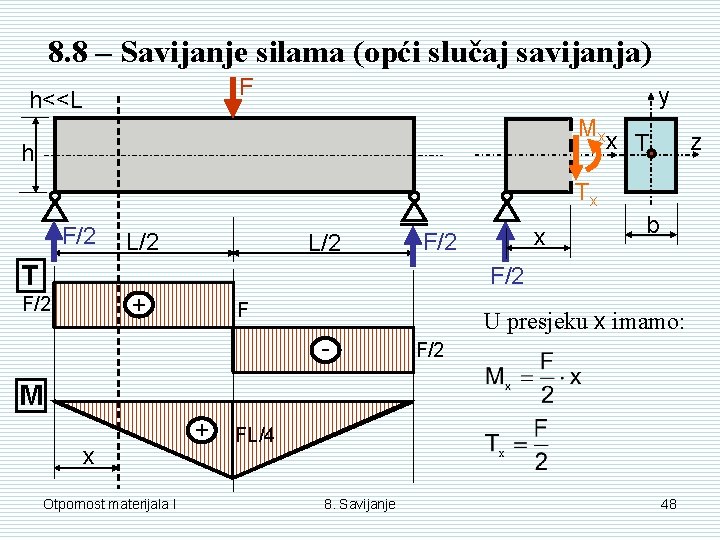
8. 8 – Savijanje silama (opći slučaj savijanja) F h<<L y Mx h x T z Tx F/2 T L/2 x F/2 b F/2 + F/2 F - U presjeku x imamo: F/2 M x Otpornost materijala I + FL/4 8. Savijanje 48

Zaključak: Kod savijanja silama u poprečnom presjeku se javljaju i moment savijanja, koji izaziva pojavu normalnih naprezanja, i poprečna sila, koja izaziva pojavu posmičnih naprezanja. Prema tome, poprečni presjeci ne ostaju ravni već se vitopere. Postoji međudjelovanje između uzdužnih vlakanaca. Posljedica: Vlakanca se ne nalaze u jednoosnom (1 D) stanju naprezanja, već u dvoosnom stanju naprezanja (2 D). Pitanje: Kako odrediti ta normalna i posmična naprezanja? Otpornost materijala I 8. Savijanje 49

Određivanje normalnih naprezanja pri savijanju silama: - radi se o maloj pogrešci - proračun se pojednostavljuje - naime, utjecaj poprečne sile na normalna naprezanja za slučaj h<<L je zanemariv (veličina ovog utjecaja će se pokazati kasnije) Zaključak: Izraz za određivanje normalnih naprezanja je jednak i za slučaj čistog savijanja i za slučaj savijanja silama! Otpornost materijala I 8. Savijanje 50

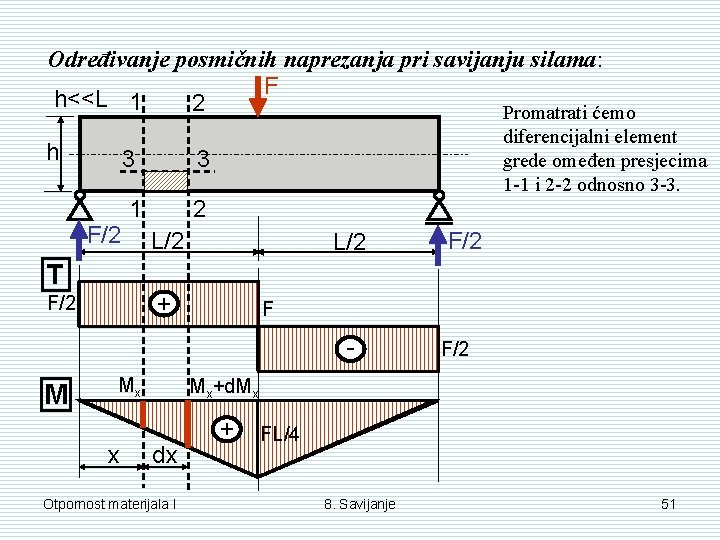
Određivanje posmičnih naprezanja pri savijanju silama: F h<<L 1 2 Promatrati ćemo h F/2 3 3 1 2 T diferencijalni element grede omeđen presjecima 1 -1 i 2 -2 odnosno 3 -3. L/2 + F/2 F - M Mx x F/2 Mx+d. Mx dx Otpornost materijala I + FL/4 8. Savijanje 51

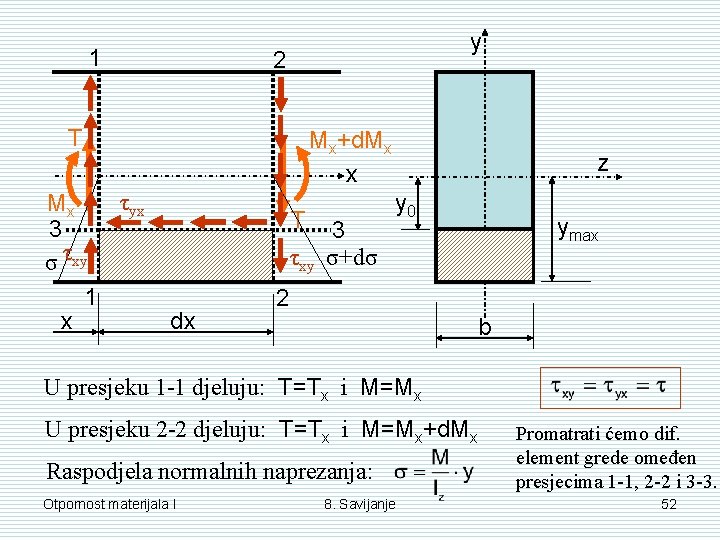
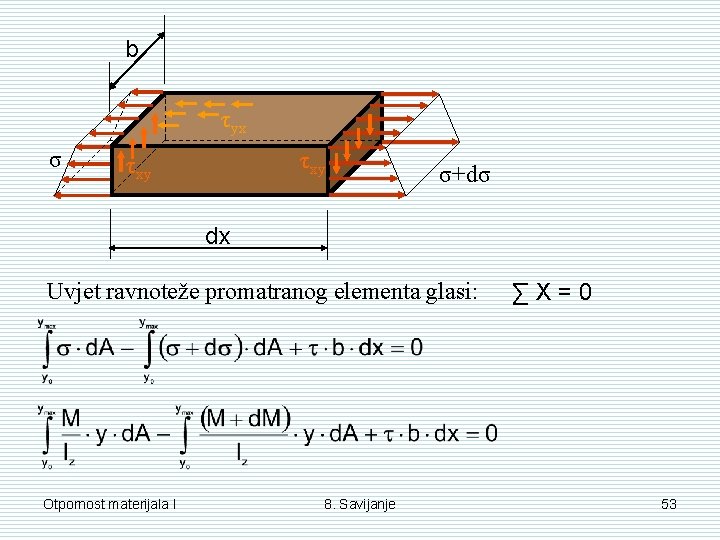
1 y 2 T τyx Mx 3 σ τxy 1 x Mx+d. Mx x T τxy dx 3 σ+dσ z y 0 ymax 2 b U presjeku 1 -1 djeluju: T=Tx i M=Mx U presjeku 2 -2 djeluju: T=Tx i M=Mx+d. Mx Raspodjela normalnih naprezanja: Otpornost materijala I 8. Savijanje Promatrati ćemo dif. element grede omeđen presjecima 1 -1, 2 -2 i 3 -3. 52

b τyx σ τxy σ+dσ dx Uvjet ravnoteže promatranog elementa glasi: Otpornost materijala I 8. Savijanje ∑X=0 53

pri čemu je: statički moment površine A 1 obzirom na neutralnu os z. Ostaje nam: Kako je konačni izraz za posmična naprezanja kod savijanja silama glasi: Otpornost materijala I 8. Savijanje 54

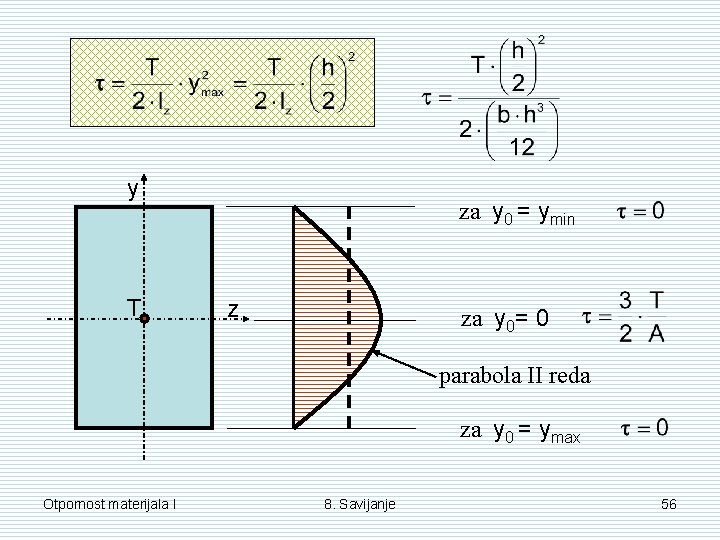
Primjer: Određivanje posmičnih naprezanja kod savijanja silama za pravokutni poprečni presjek y Izraz za određivanje posmičnih naprezanja: h/2 z T h y 0 h/2 A 1 b ymax za y 0 = ymax za y 0= 0 Otpornost materijala I 8. Savijanje 55

y T za y 0 = ymin z za y 0= 0 parabola II reda za y 0 = ymax Otpornost materijala I 8. Savijanje 56

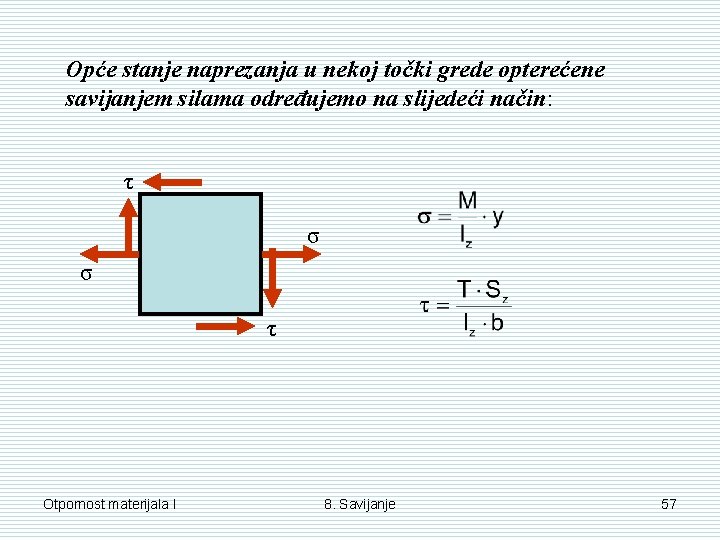
Opće stanje naprezanja u nekoj točki grede opterećene savijanjem silama određujemo na slijedeći način: τ σ σ τ Otpornost materijala I 8. Savijanje 57

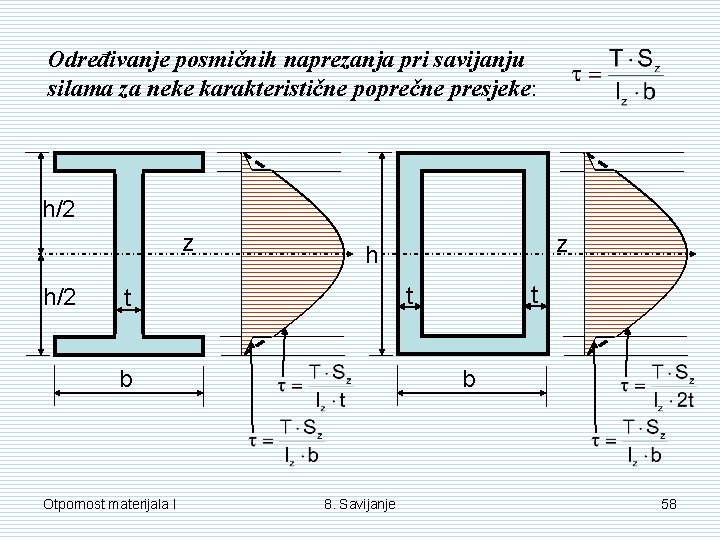
Određivanje posmičnih naprezanja pri savijanju silama za neke karakteristične poprečne presjeke: h/2 z h/2 t t t b Otpornost materijala I z h b 8. Savijanje 58

Zaključci / Napomene: Dijagram posmičnih naprezanja uslijed poprečne sile kod savijanja silama ovisi o obliku poprečnog presjeka. Posmična naprezanja su jednaka nuli u krajnjim vlakancima odnosno u vlakancima koja su najudaljenija od neutralnog sloja. Posmična naprezanja imaju najveću vrijednost u neutralnom sloju: Otpornost materijala I 8. Savijanje 59

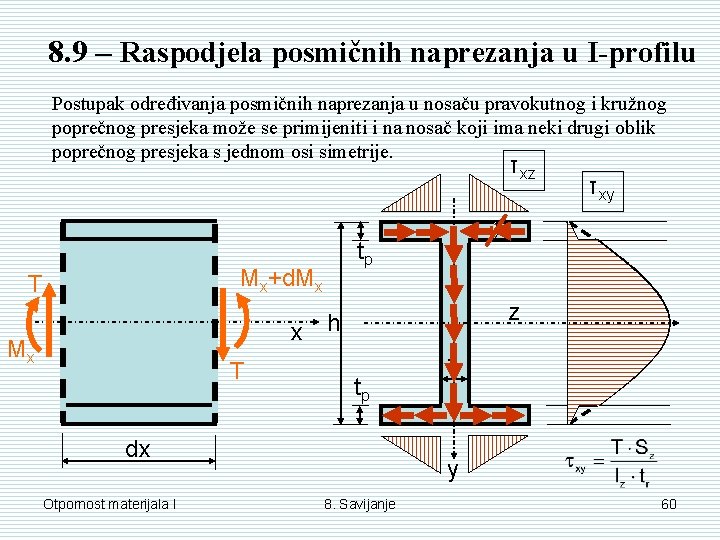
8. 9 – Raspodjela posmičnih naprezanja u I-profilu Postupak određivanja posmičnih naprezanja u nosaču pravokutnog i kružnog poprečnog presjeka može se primijeniti i na nosač koji ima neki drugi oblik poprečnog presjeka s jednom osi simetrije. τxz tp Mx+d. Mx T z x h Mx T tp dx Otpornost materijala I τxy tr y 8. Savijanje 60

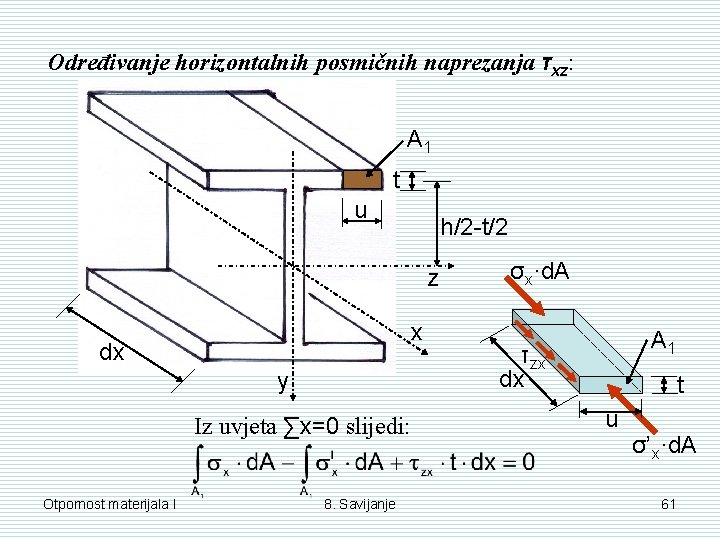
Određivanje horizontalnih posmičnih naprezanja τxz: A 1 t u h/2 -t/2 z x dx y Iz uvjeta ∑x=0 slijedi: Otpornost materijala I 8. Savijanje σx·d. A A 1 τzx dx t u σ’x·d. A 61

Kako je: uz: Konačno dobivamo: Otpornost materijala I 8. Savijanje Vidimo da je promjena τzx i τxz linearna. 62

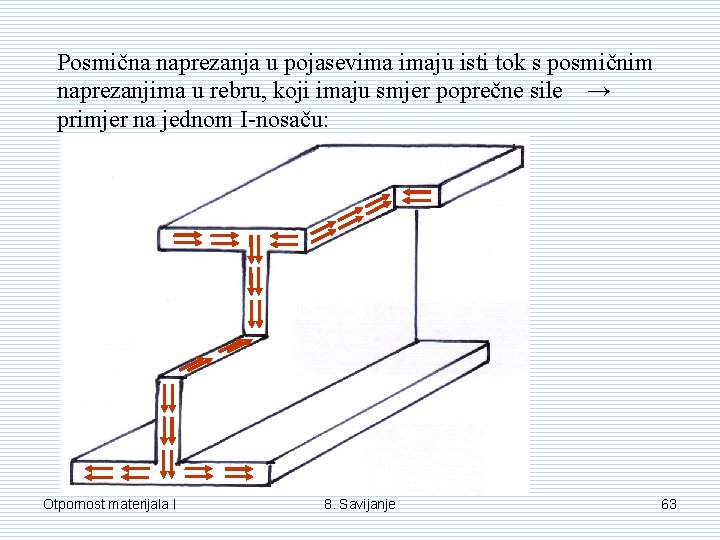
Posmična naprezanja u pojasevima imaju isti tok s posmičnim naprezanjima u rebru, koji imaju smjer poprečne sile → primjer na jednom I-nosaču: Otpornost materijala I 8. Savijanje 63

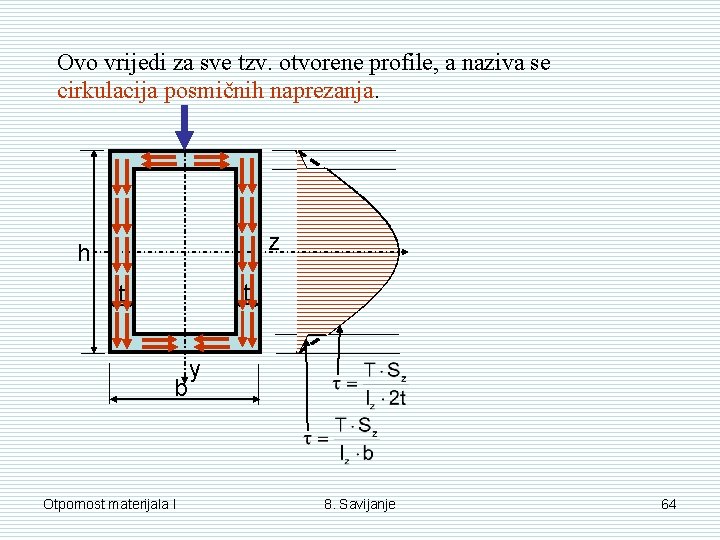
Ovo vrijedi za sve tzv. otvorene profile, a naziva se cirkulacija posmičnih naprezanja. z h t t b Otpornost materijala I y 8. Savijanje 64

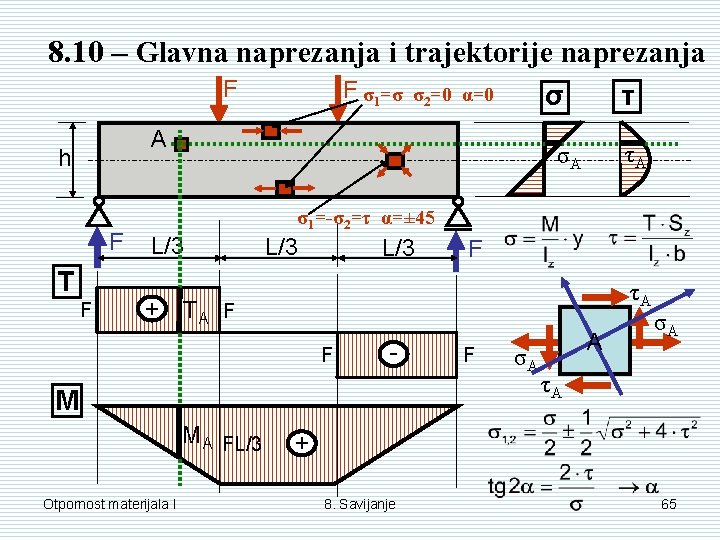
8. 10 – Glavna naprezanja i trajektorije naprezanja F F σ1=σ σ2=0 α=0 A h F T F τ σ τA σA σ1=-σ2=τ α=± 45 L/3 + L/3 τA TA F F - M MA FL/3 Otpornost materijala I F F σA A σA τA + 8. Savijanje 65

Trajektorije glavnih naprezanja su linije koje u konstrukciji spajaju točke s jednakim glavnim naprezanjima. Kroz svaku točku prolaze dvije trajektorije glavnih naprezanja – vlačna (puna linija) i tlačna (crtkana linija) trajektorija. (slika 14. 45, str. 351) Otpornost materijala I 8. Savijanje 66

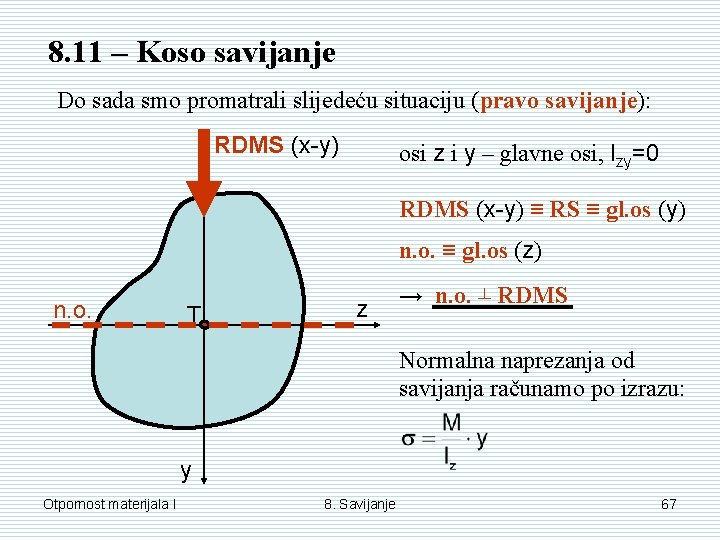
8. 11 – Koso savijanje Do sada smo promatrali slijedeću situaciju (pravo savijanje): RDMS (x-y) osi z i y – glavne osi, Izy=0 RDMS (x-y) ≡ RS ≡ gl. os (y) n. o. ≡ gl. os (z) n. o. T z → n. o. ┴ RDMS Normalna naprezanja od savijanja računamo po izrazu: y Otpornost materijala I 8. Savijanje 67

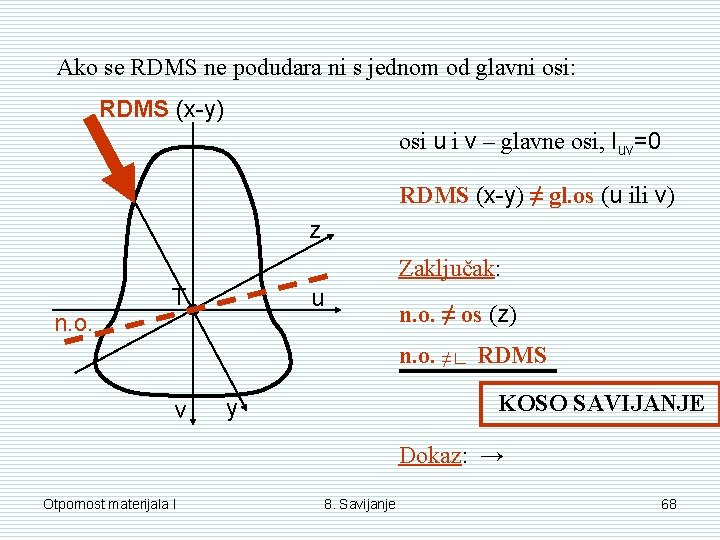
Ako se RDMS ne podudara ni s jednom od glavni osi: RDMS (x-y) osi u i v – glavne osi, Iuv=0 RDMS (x-y) ≠ gl. os (u ili v) z Zaključak: n. o. T u n. o. ≠ os (z) n. o. ≠∟ RDMS v KOSO SAVIJANJE y Dokaz: → Otpornost materijala I 8. Savijanje 68

Dokaz: Pretpostavimo da je os z neutralna os poprečnog presjeka! To znači da trebaju biti ispunjeni slijedeći uvjeti ravnoteže: (1) ∑X = 0 (2) ∑M(y) = 0 (3) ∑M(z) = M Jedn. (2) raspisana glasi: Vrijedi pretpostavka o ravnim presjecima te imamo: To uvrstimo gore i dobivamo: Kako je treba biti =0 slijedi da Pošto osi z i y nisu glavne osi, to slijedi da Zaključak: Neutralna os nije os z; neutralna os nije okomita na RDMS; RDMS ne poklapa se ni s jednom glavnom osi. Otpornost materijala I 8. Savijanje 69

Rekapitulacija: Kod kosog savijanja, ravnina djelovanja momenta savijanja (ravnina djelovanja opterećenja) ne poklapa se ni s jednom glavnom osi poprečnog presjeka. Kod kosog savijanja, ravnina djelovanja momenta savijanja i ravnina savijanja se ne podudaraju. Kod kosog savijanja, neutralna os poprečnog presjeka nije okomita na ravninu djelovanja momenta savijanja (naime, neutralna os je uvijek okomita na ravninu savijanja). Otpornost materijala I 8. Savijanje 70

Promatrajmo slijedeću situaciju (koso savijanje): RDMS osi u i v – glavne osi, Iuv=0 v Kut α je pozitivan ako se otvara od +v prema +u. α M Mv α T Mu u Imamo koso savijanje jer se RDMS ne poklapa ni s jednom glavnom osi, u ili v. Koristimo princip superpozicije: Mu=M·cosα Otpornost materijala I 8. Savijanje Mv=M·sinα 71

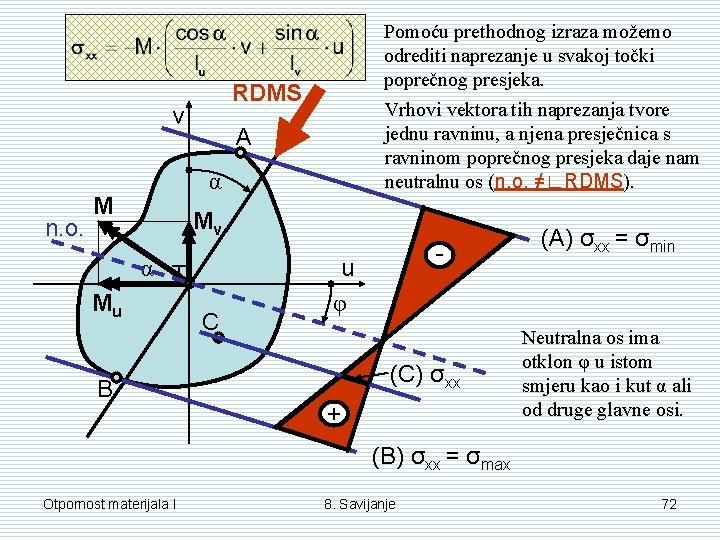
RDMS v n. o. Pomoću prethodnog izraza možemo odrediti naprezanje u svakoj točki poprečnog presjeka. Vrhovi vektora tih naprezanja tvore jednu ravninu, a njena presječnica s ravninom poprečnog presjeka daje nam neutralnu os (n. o. ≠∟RDMS). A α M Mv α T Mu B C - u φ (C) σxx + (A) σxx = σmin Neutralna os ima otklon φ u istom smjeru kao i kut α ali od druge glavne osi. (B) σxx = σmax Otpornost materijala I 8. Savijanje 72

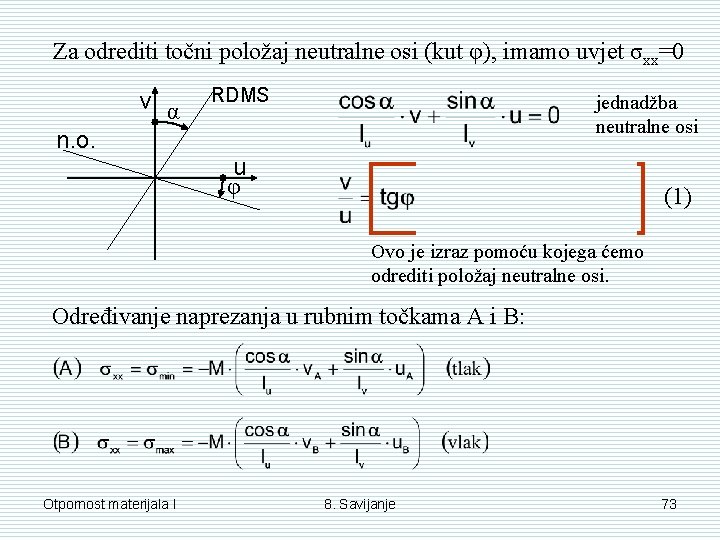
Za odrediti točni položaj neutralne osi (kut φ), imamo uvjet σxx=0 v α RDMS jednadžba neutralne osi n. o. u φ (1) Ovo je izraz pomoću kojega ćemo odrediti položaj neutralne osi. Određivanje naprezanja u rubnim točkama A i B: Otpornost materijala I 8. Savijanje 73

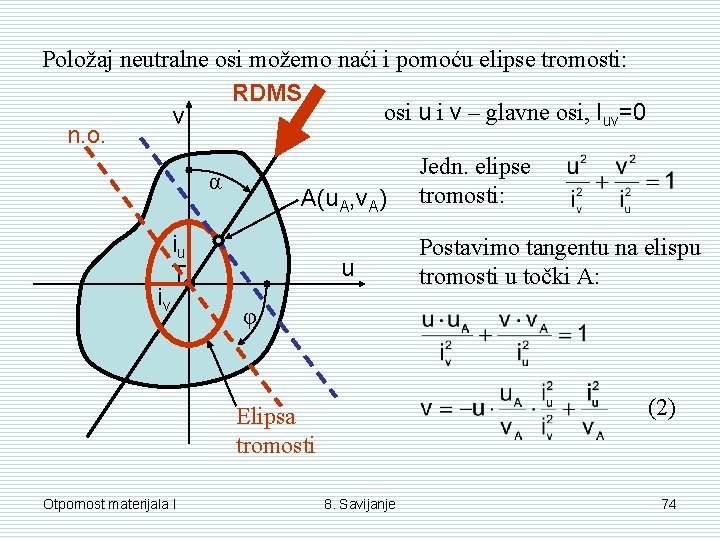
Položaj neutralne osi možemo naći i pomoću elipse tromosti: RDMS osi u i v – glavne osi, Iuv=0 v n. o. Jedn. elipse α A(u. A, v. A) tromosti: iv iu T u φ (2) Elipsa tromosti Otpornost materijala I Postavimo tangentu na elispu tromosti u točki A: 8. Savijanje 74

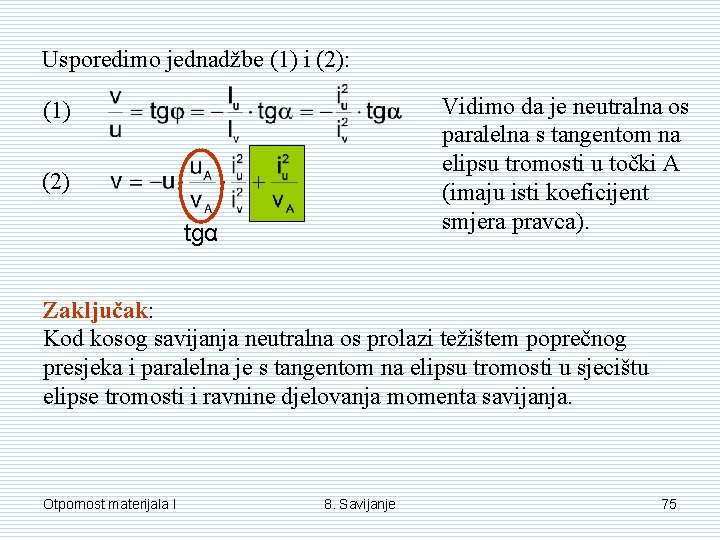
Usporedimo jednadžbe (1) i (2): Vidimo da je neutralna os paralelna s tangentom na elipsu tromosti u točki A (imaju isti koeficijent smjera pravca). (1) (2) tgα Zaključak: Kod kosog savijanja neutralna os prolazi težištem poprečnog presjeka i paralelna je s tangentom na elipsu tromosti u sjecištu elipse tromosti i ravnine djelovanja momenta savijanja. Otpornost materijala I 8. Savijanje 75

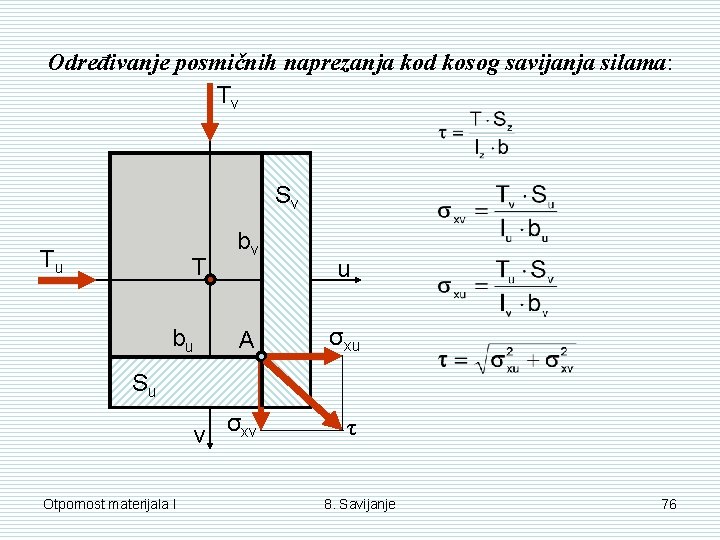
Određivanje posmičnih naprezanja kod kosog savijanja silama: Tv Sv Tu T bv u A σxu v σxv τ bu Su Otpornost materijala I 8. Savijanje 76

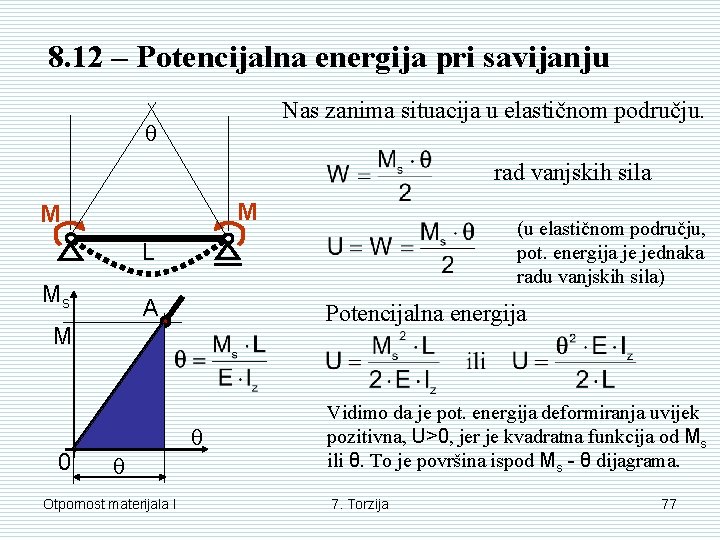
8. 12 – Potencijalna energija pri savijanju Nas zanima situacija u elastičnom području. θ rad vanjskih sila M M (u elastičnom području, pot. energija je jednaka radu vanjskih sila) L Ms A Potencijalna energija M 0 θ θ Otpornost materijala I Vidimo da je pot. energija deformiranja uvijek pozitivna, U>0, jer je kvadratna funkcija od Ms ili θ. To je površina ispod Ms - θ dijagrama. 7. Torzija 77

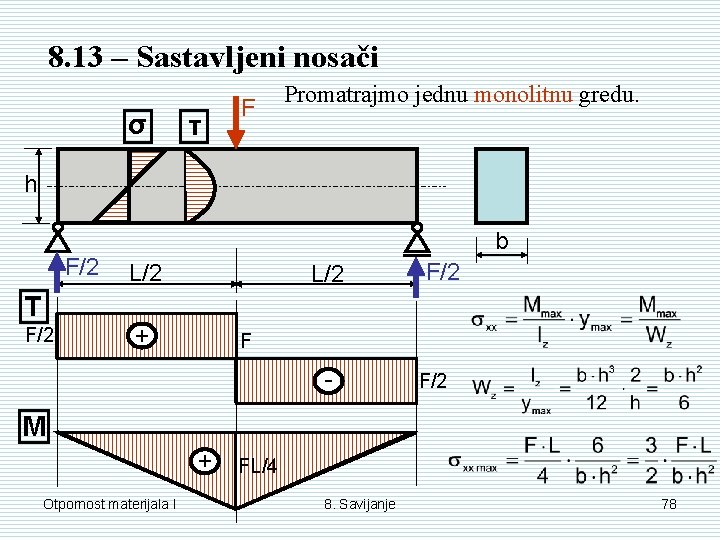
8. 13 – Sastavljeni nosači σ τ F Promatrajmo jednu monolitnu gredu. h F/2 T F/2 b L/2 + F/2 F - F/2 M + Otpornost materijala I FL/4 8. Savijanje 78

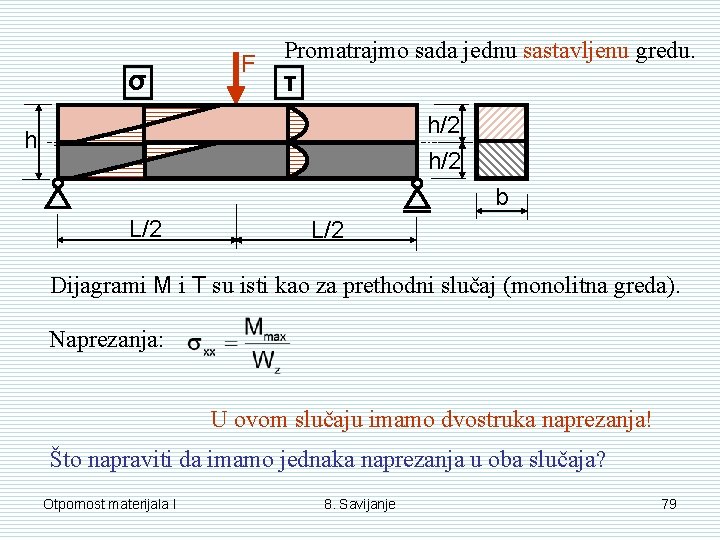
σ F Promatrajmo sada jednu sastavljenu gredu. τ h/2 h b L/2 Dijagrami M i T su isti kao za prethodni slučaj (monolitna greda). Naprezanja: U ovom slučaju imamo dvostruka naprezanja! Što napraviti da imamo jednaka naprezanja u oba slučaja? Otpornost materijala I 8. Savijanje 79

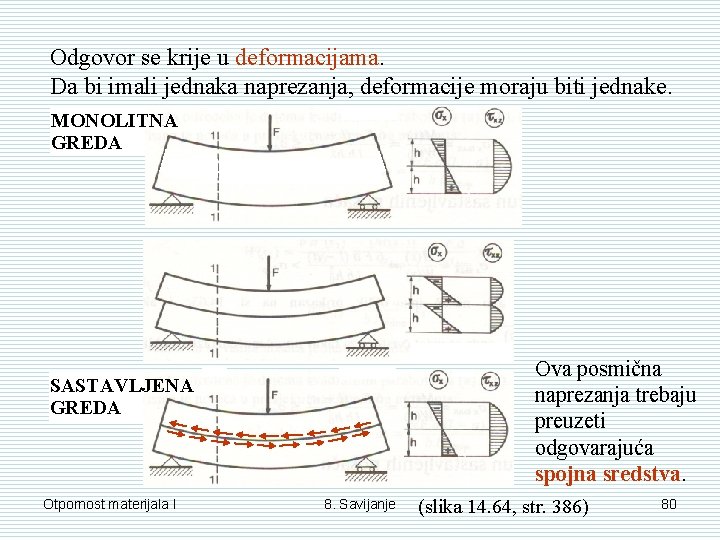
Odgovor se krije u deformacijama. Da bi imali jednaka naprezanja, deformacije moraju biti jednake. MONOLITNA GREDA Ova posmična naprezanja trebaju preuzeti odgovarajuća spojna sredstva. SASTAVLJENA GREDA Otpornost materijala I 8. Savijanje (slika 14. 64, str. 386) 80

Zaključak: Proračun sastavljenog nosača se provodi tako da najprije proračunamo nosač kao da je monolitan (unutarnje sile i naprezanja) a zatim proračunavamo spojna sredstva koja moraju preuzeti posmična naprezanja/sile. Detaljnije se o raznim situacijama može vidjeti u knjizi na str. 387 -400. Otpornost materijala I 8. Savijanje 81

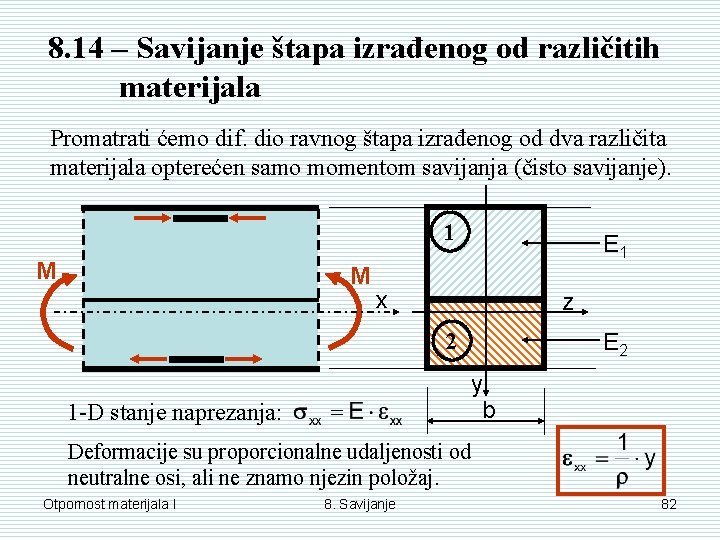
8. 14 – Savijanje štapa izrađenog od različitih materijala Promatrati ćemo dif. dio ravnog štapa izrađenog od dva različita materijala opterećen samo momentom savijanja (čisto savijanje). 1 M M E 1 x z 2 E 2 y b 1 -D stanje naprezanja: Deformacije su proporcionalne udaljenosti od neutralne osi, ali ne znamo njezin položaj. Otpornost materijala I 8. Savijanje 82

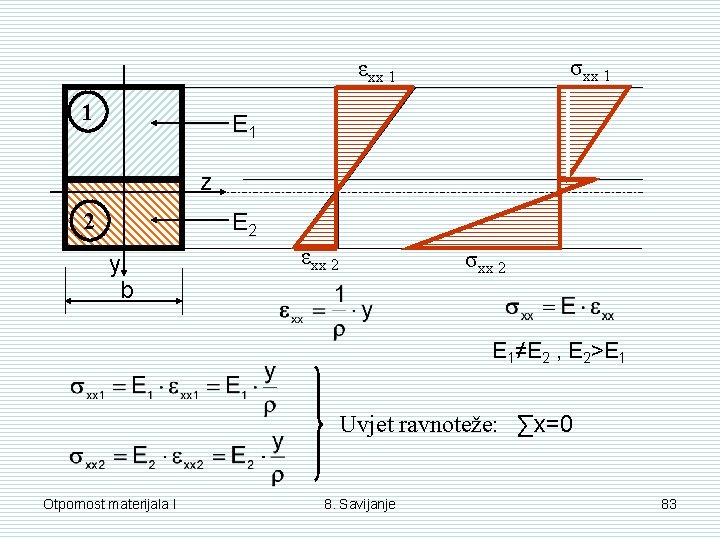
σxx 1 εxx 1 1 E 1 z 2 E 2 y b εxx 2 σxx 2 E 1≠E 2 , E 2>E 1 Uvjet ravnoteže: ∑x=0 Otpornost materijala I 8. Savijanje 83

Jednadžba neutralne osi Da je E 1=E 2 to bi bila jedn. težišta. Sada postavljamo drugu jednadžbu ravnoteže: ∑M(z)=M Iz 1 Otpornost materijala I Iz 2 8. Savijanje 84

Iz prethodnog izraza slijedi izraz za deformaciju: Za slučaj da je E 1=E 2=E imali bi da je Iz 1+Iz 2=Iz Sada možemo napisati izraze za naprezanja: Ovi izrazi su malo složeni, te se može postaviti pitanje da li se oni mogu svesti na poznati nam izraz: To možemo napraviti pomoću reduciranog poprečnog presjeka, tj. poprečni presjek reduciramo samo na jedan materijal. Otpornost materijala I 8. Savijanje 85

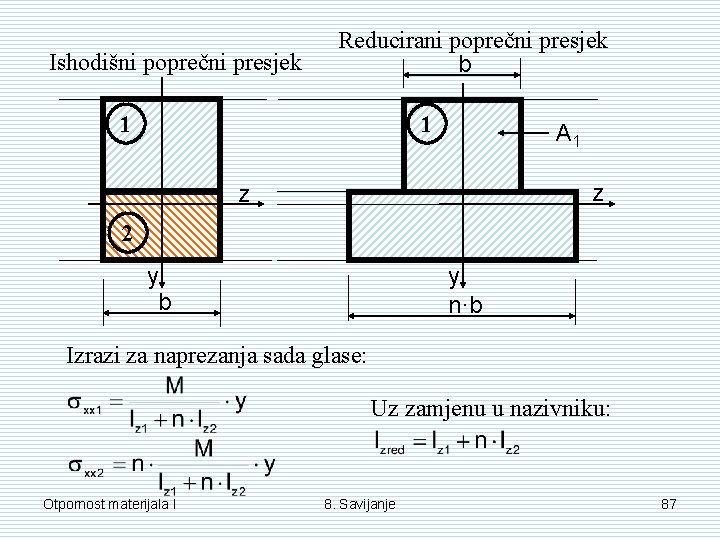
Da bi taj reducirani poprečni presjek bio ekvivalentan ishodišnom poprečnom presjeku trebaju biti zadovoljeni slijedeći uvjeti: 1) Položaj neutralne osi mora ostati nepromijenjen; 2) U ishodišnom i u reduciranom poprečnom presjeku imamo isti moment savijanja. Uz jednadžba neutralne osi glasi: Iz ovog izraza se vidi da se reducirani poprečni presjek sastoji iz samo jednog materijala (u našem slučaju to je materijal 1). Nadalje, vidimo da smo ishodišni presjek reducirali tako da površina A 1 ostaje nepromijenjena, dok je površina A 2 dana sa širinom n·b, pri čemu y ostaje nepromijenjen. Otpornost materijala I 8. Savijanje 86

Ishodišni poprečni presjek Reducirani poprečni presjek b 1 1 A 1 z z 2 y b y n·b Izrazi za naprezanja sada glase: Uz zamjenu u nazivniku: Otpornost materijala I 8. Savijanje 87

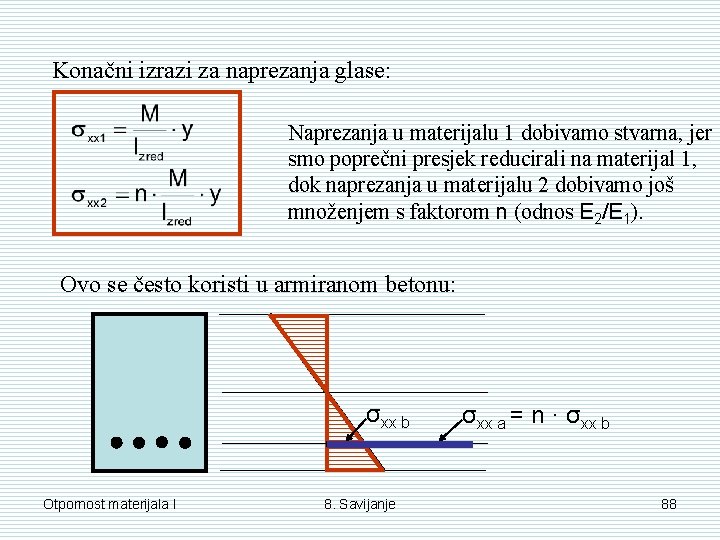
Konačni izrazi za naprezanja glase: Naprezanja u materijalu 1 dobivamo stvarna, jer smo poprečni presjek reducirali na materijal 1, dok naprezanja u materijalu 2 dobivamo još množenjem s faktorom n (odnos E 2/E 1). Ovo se često koristi u armiranom betonu: σxx b Otpornost materijala I 8. Savijanje σxx a = n · σxx b 88

Kraj gradiva u zimskom semestru. Vidimo se u ljetnom semestru. Otpornost materijala I Kraj nastave u zimskom semestru 89