Part III Markov Chains Queueing Systems 10 DiscreteTime

Part III Markov Chains & Queueing Systems 10. Discrete-Time Markov Chains 11. Stationary Distributions & Limiting Probabilities 12. State Classification 13. Limiting Theorems For Markov Chains 14. Continuous-Time Markov Chains 1

10. Discrete-Time Markov Chain Definition of Markov Processes A random process is said to be a Markov Process if, for any set of n time points t 1<t 2<…<tn in the index set or time range of the process, the conditional distribution of X(tn), given the values of X(t 1), X(t 2), …, X(tn-1), depends only on the immediately preceding value; that is, for any real numbers x 1, x 2, …, xn, 2

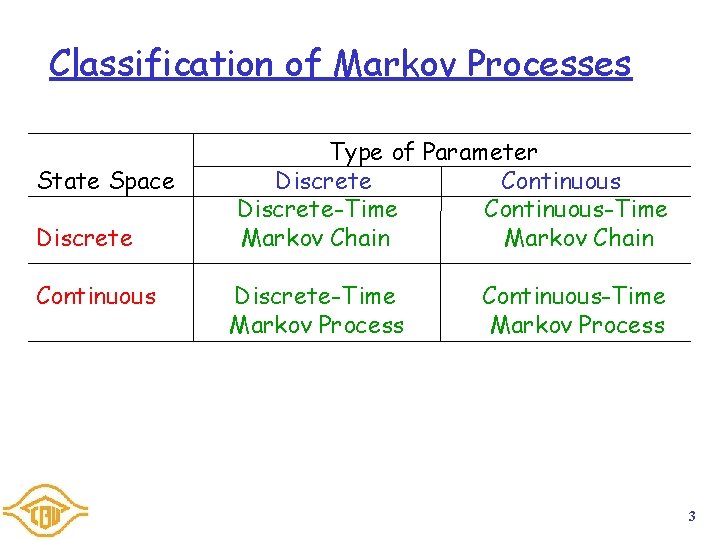
Classification of Markov Processes State Space Discrete Continuous Type of Parameter Discrete Continuous Discrete-Time Continuous-Time Markov Chain Discrete-Time Markov Process Continuous-Time Markov Process 3

Discrete-Time Markov Chain Definition： A discrete-time Markov chain {Xn| n=0, 1, 2, …}, is a discrete-time, discrete-value random sequence such that given X 0, X 1, …, Xn, the next random variable depends only on Xn through the transition probability 4

Theorem 10. 1 The transition probabilities pij of a Markov chain satisfy Pf： 5

Example 10. 1 The two-state Markov chain can be used to model a wide variety of systems that alternate between ON and OFF states. After each unit of time in the OFF state, the system turns ON with probability p. After each unit of time in the ON state, the system turns OFF with probability q. Using 0 and 1 to denote the OFF and ON states, what is the Markov chain for the system? Sol： 6

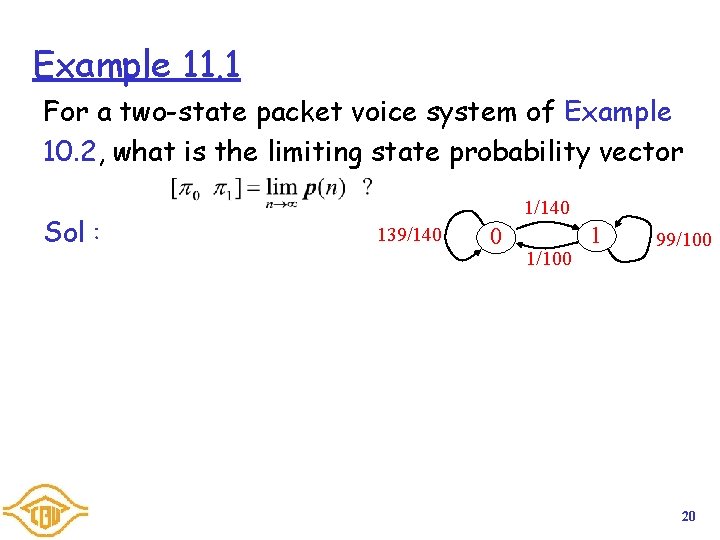
Example 10. 2 A packet voice communications is in talkspurts (state 1) or silent (state 0) states. The system decides whether the speaker is talking or silent every 10 ms (slot time). If the speaker is silent in a slot, then the speaker will be talking in the next slot with probability p= 1/140. If the speaker is talking in a slot, the speaker will be silent in the next slot with probability q = 1/100. Sketch the Markov chain of this system. Sol： 7

Example 10. 3 A computer disk drive can be in one of 3 possible states: 0 (IDLE), 1 (READ), or 2 (WRITE). When a unit of time is required to read or write a sector on the disk, sketch the Markov chain. Sol： 8

Example 10. 4 In a discrete random walk, a person’s position is marked by an integer on the real line. Each unit of time, the person randomly moves one step, either to the right (with probability p) or to the left. Sketch the Markov chain. Sol： 9

Example 10. 5 What is the transition matrix of the two-state ONOFF Markov chain of Example 10. 1 ? Sol： 10

n-Step Transition Probabilities Definition For a finite Markov chain, the n-step transition probabilities are given by the matrix P(n) which has i, j-th element 11

Theorem 10. 2 : Chapman-Kolmogorov Eq. For a finite Markov chain with K states, the n-step transition probabilities satisfy Pf： 12

Theorem 10. 3 For a finite Markov chain with transition matrix P, the n-step transition matrix is Pf： 13

Example 10. 6 For the two-state Markov chain described in Example 10. 1, find the n-step transition matrix P(n). Given the system is OFF at time 0, what is the probability the system is OFF at time n = 33 ? Pf： 14

State Probability Vector Definition A vector p=[p 0 p 1 … p. K] is a state probability vector if , and each element is nonnegative. 15

Theorem 10. 4 The state probabilities pj(n) at time n can be defined by either one iteration with the n-step transition probabilities: or n iterations with the one-step transition probabilities: Pf： 16

Example 10. 7 For the two-state Markov chain described in Example 10. 1 with initial state probabilities p(0)=[p 0 p 1], find the state probability vector p(n). Sol： 17

Part III Markov Chains & Queueing Systems 10. Discrete-Time Markov Chains 11. Stationary Distributions & Limiting Probabilities 12. State Classification 13. Limiting Theorems For Markov Chains 14. Continuous-Time Markov Chains 18

11. Stationary Distributions & Limiting Probabilities Definition of Limiting State Probabilities For a finite Markov chain with initial state probability vector p(0) , the limiting state probabilities, when they exist, are defined to be the vector 19

Example 11. 1 For a two-state packet voice system of Example 10. 2, what is the limiting state probability vector Sol： 1/140 139/140 0 1/100 1 99/100 20

Theorem 11. 1 If a finite Markov chain with transition matrix P and initial state probability p(0) has limiting probability vector , then Pf： 21

Stationary Probability Vector Definition For a finite Markov chain with transition matrix P, a state probability vector is stationary if 22

Theorem 11. 2 If a finite Markov chain Xn with transition matrix P is initialized with stationary probability vector p(0) = , then p(n) = for all n and the stochastic process Xn is stationary. Pf： 23

Example 11. 2 A queueing system is described by a Markov chain in which that state Xn is the number of customers in the queue at time n. The Markov chain has a unique stationary distribution . The following questions are all equivalent. (1) What is the steady-state probability of at least 10 customers in the system? (2) If we inspect the queue in the distant future, what is the probability of at least 10 customers in the system? (3) What is the stationary probability of at least 10 customers in the system? (4) What is the limiting probability of at least 10 customers in the system? 24

Example 11. 3 Consider the two-state Markov chain of Example 10. 1 and Example 10. 6. For what values of p and q does (a) exist, independent of the initial state probability vector p(0); (b) exist, but depend on p(0); (c) or not exist? Sol： 25

Part III Markov Chains & Queueing Systems 10. Discrete-Time Markov Chains 11. Stationary Distributions & Limiting Probabilities 12. State Classification 13. Limiting Theorems For Markov Chains 14. Continuous-Time Markov Chains 26

12. State Classification Accessibility State j is accessible from state i, written i j, if pij(n) > 0 for some n > 0. Communicating States State i and j communicates, written i j, if i j and j i. Communicating Class A communicating class is a nonempty subset of states C such that if i C , then j C if and only if i j. 27

State Classification Periodic and Aperiodic State i has period d if d is the largest integer such that pii(n) = 0 whenever n is not divisible by d (pii(n) > 0 whenever n is divisible by d). If d = 1, then state i is called aperiodic. Transient and Recurrent States In a finite Markov chain, a state i is transient if there exists a state j such that i j but j i; otherwise, if no such state j exists, then state i is recurrent. Irreducible Markov chain A Markov chain is irreducible if there is only one communicating class. 28

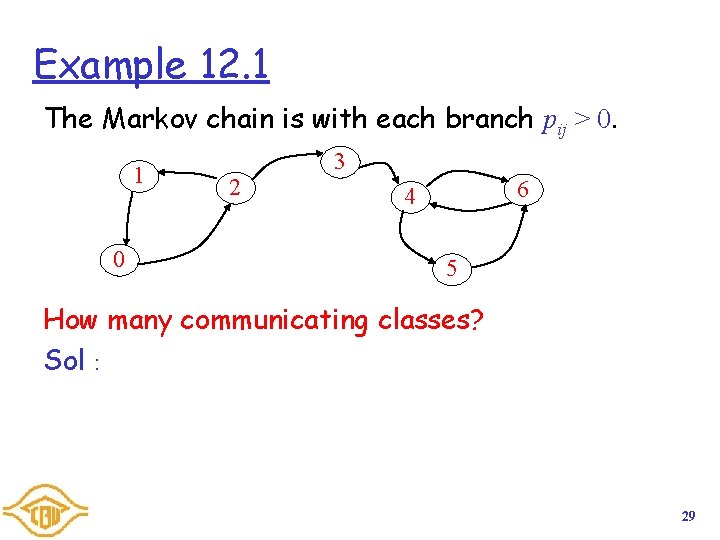
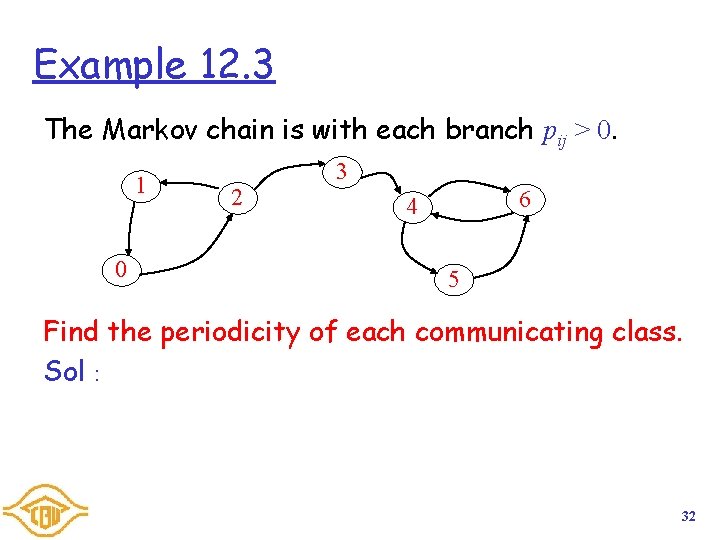
Example 12. 1 The Markov chain is with each branch pij > 0. 1 0 2 3 6 4 5 How many communicating classes? Sol： 29

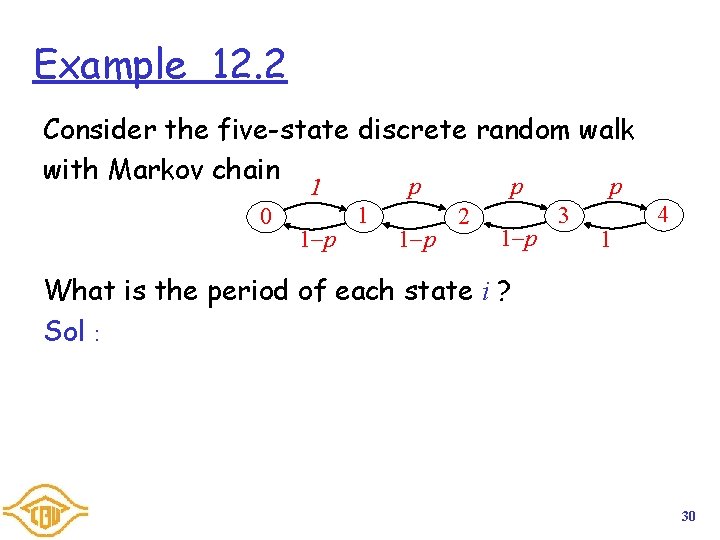
Example 12. 2 Consider the five-state discrete random walk with Markov chain 0 1 p p p 1 1 1 p 2 1 p p 3 1 4 What is the period of each state i ? Sol： 30

Theorem 12. 1 Communicating states have the same period. Pf： 31

Example 12. 3 The Markov chain is with each branch pij > 0. 1 0 2 3 6 4 5 Find the periodicity of each communicating class. Sol： 32

Theorem 12. 2 If i is recurrent and i j, then j is recurrent. Sol： 33

Example 12. 4 The Markov chain is with each branch pij > 0. 0 1 2 3 4 5 Identify each communicating class and indicate whether it is transient or recurrent. Sol： 34

Theorem 12. 3 If state i is transient, then Ni, the number of visits to state i over all time, has expected value E[Ni] < . Pf： 35

Theorem 12. 4 A finite-state Markov chain always has a recurrent communicating class. Pf： 36

Example 12. 5 The Markov chain is with each branch pij > 0. 0 1 2 3 4 5 If the system starts in state j C 1 = {0, 1, 2}, the system never leaves C 1. If the system starts in communicating class C 3 = {4, 5}, the system never leaves C 3. If the system starts in the transient state 3, then in the first step there is a random transition to either state 2 or to state 4 and the system then remains forever in the corresponding communicating class. 37

Part III Markov Chains & Queueing Systems 10. Discrete-Time Markov Chains 11. Stationary Distributions & Limiting Probabilities 12. State Classification 13. Limiting Theorems For Markov Chains 14. Continuous-Time Markov Chains 38

13. Limiting Theorems For Markov Chains For Markov chains with multiple recurrent classes, the limiting state probabilities depend on the initial state distribution. For understanding a system with multiple communicating classes, we need to examine each recurrent class separately as an irreducible system consisting of just that class. In this part, we first focus on irreducible, aperiodic chains and their limiting state probabilities. 39

Theorem 13. 1 For an irreducible, aperiodic, finite Markov chain with states {0, 1, 2, …, K}, the limiting n-step transition matrix is where is the column vector the unique vector satisfying and is 40

Theorem 13. 1 (cont’d) Pf： 41

Theorem 13. 2 For an irreducible, aperiodic, finite Markov chain with transition matrix P and initial state probability vector p(0) , Pf： 42

Example 13. 1 For the packet voice communications system of Example 12. 8, use Theorem 13. 2 to calculate the stationary 1/140 probabilities. 139/140 1 0 99/100 Sol： 1/100 43

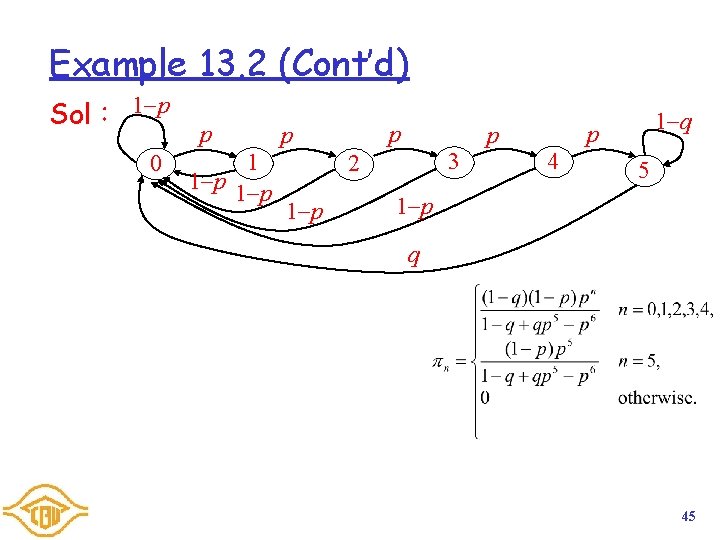
Example 13. 2 A digital mobile phone transmits one packet in every 20 -ms time slot over a wireless connection. A packet is received error with probability p = 0. 1, independent of other packets. Whenever 5 consecutive packets are received in error, the transmitter enters a timeout state. During the timeout state, the mobile terminal performs an independent Bernoulli trial with success probability q = 0. 01 in every slot. When a success occurs, the mobile terminal starts transmitting in the next slot as though no packets had been in error. Construct a Markov chain for this system. What are the limiting state probabilities? 44

Example 13. 2 (Cont’d) Sol： 1 p 0 p 1 1 p p p p 3 2 1 p 1 q p 4 5 1 p q 45

Theorem 13. 3 Consider an irreducible, aperiodic, finite Markov chain with transition probabilities {pij} and stationary probabilities { i}. For any partition of the state space into disjoint subsets S and S’, Pf： 46

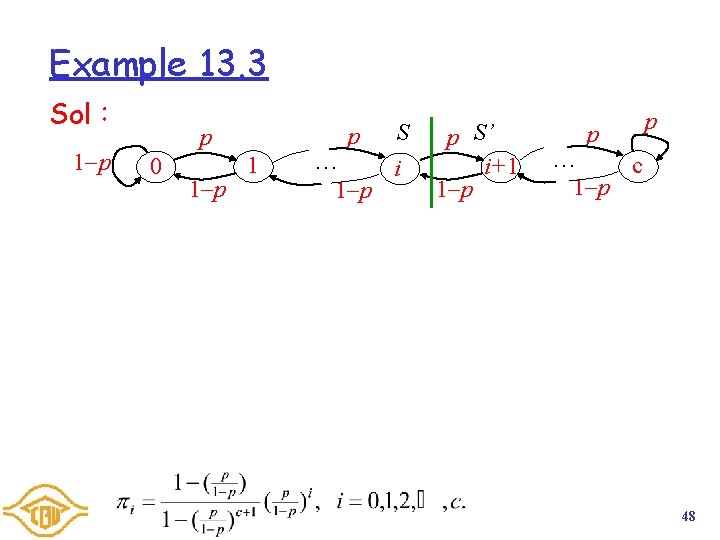
Example 13. 3 In each time slot, a router can either store an arriving data packet in its buffer or forward a stored packet (and remove that packet from its buffer). In each time slot, a new packet arrives with probability p, independent of arrivals in all other slots. This packets is stored as long as the router is storing fewer than c packets. If c packets are already buffered, then the new packet is discarded by the router. If no new packet arrives and n > 0 packets are buffered by the router, then the router will forward one buffered packet. That packet is then removed from the router. Let Xn denote the number of buffered packets at time n. Sketch the Markov chain for Xn and find the stationary probabilities. 47

Example 13. 3 Sol： 1 p p p 0 1 p 1 … 1 p S i p S’ i+1 1 p p p … c 1 p 48

Periodic States and Multiple Communicating Classes Theorem 13. 4： For an irreducible, recurrent, periodic, finite Markov chain with transition matrix P, the stationary probability vector is the unique nonnegative solution of Pf： 49

Example 13. 4 Find the stationary probabilities for the Markov 1 1 chain shown to the right. 1 0 2 Sol： 1 50

Theorem 13. 5 For a Markov chain with recurrent communicating classes C 1, … Cm, let denote the limiting state probabilities associated with class k. Given that the system starts in a transient state i, the limiting probability of state j is where P[Bik] is the conditional probability that the system enters class Ck. Pf： 51

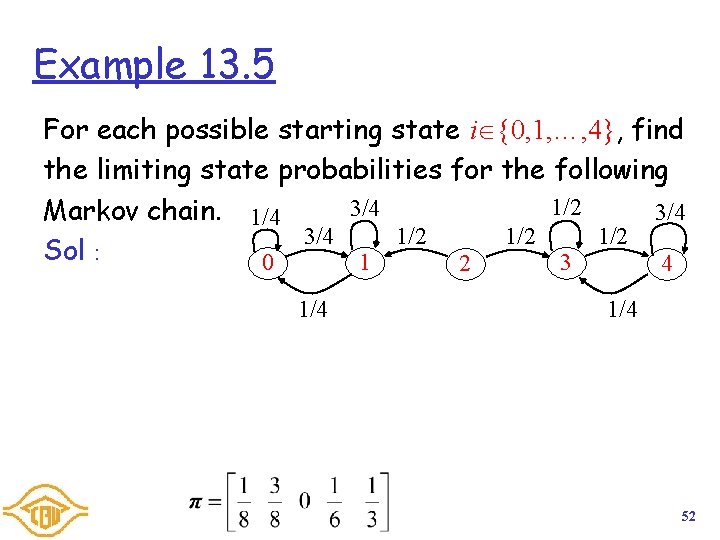
Example 13. 5 For each possible starting state i {0, 1, …, 4}, find the limiting state probabilities for the following 1/2 3/4 Markov chain. 1/4 3/4 1/2 1/2 Sol： 1 3 0 2 4 1/4 52

Countably Infinite Chains Countably infinite Markov chains has infinite set of states {0, 1, 2, …}. We will consider only a single communicating class here. (Irreducible Markov chains) Multiple communicating classes represent distinct system modes that are coupled only through an initial transient phase that results in the system landing in one of the communicating classes. 53

Example 13. 6 Suppose that the router in Example 13. 3 has unlimited buffer space. In each time slot, a router either store an arriving data packet in its buffer or forward a stored packet ( and remove that packet from its buffer). In each time slot, a new packet is stored with probability p, independent of arrivals in all other slots. If no new packet arrives, then one packet will be removed from the buffer and forwarded. Sketch the Markov chain for Xn, the number of buffered packets at time n. 1 p Sol： p p p … 1 0 2 1 p 1 p 54

Theorem 13. 6：Chapman-Kolmogorov Eqs. The n-step transition probabilities satisfy Pf：Omitted. 55

Theorem 13. 7 The state probabilities pj(n) at time n can be found by either one iteration with the n-step transition probabilities or n iterations with the one-step transition probabilities Pf：Omitted. 56

Visitation, First Return Time, No. of Returns Definitions：Given that the system is in state i at an arbitrary time, (a) Eii is the event that the system eventually returns to visit state i. (b) Tii is the time (number of transitions) until the system first returns to state i, (c) Nii is the number of times (in the future) that the system returns to state i. Definition：For a countably infinite Markov chain, state i is recurrent if P[Eii]=1; otherwise state i is transient. 57

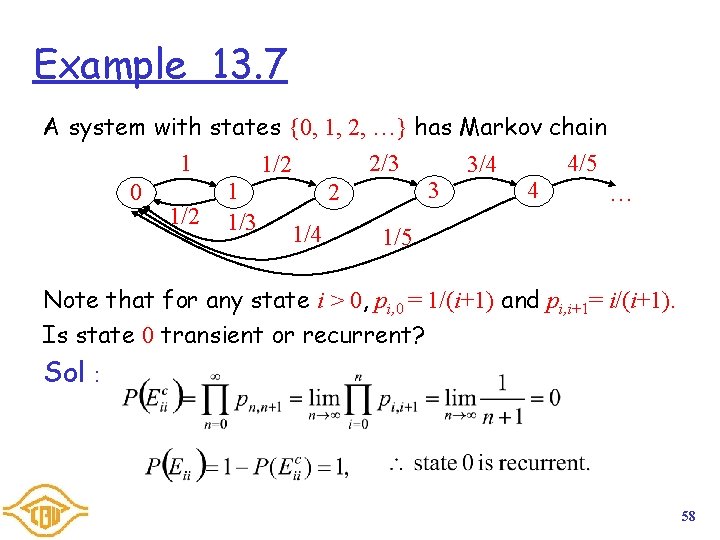
Example 13. 7 A system with states {0, 1, 2, …} has Markov chain 1 4/5 2/3 3/4 1/2 4 3 1 0 2 … 1/2 1/3 1/4 1/5 Note that for any state i > 0, pi, 0 = 1/(i+1) and pi, i+1= i/(i+1). Is state 0 transient or recurrent? Sol： 58

Theorem 13. 8 The expected number of visits to state i over all time is Pf： 59

Theorem 13. 9 State i is recurrent if and only if E[Nii]= . Pf： 60

Example 13. 8 The discrete random walk introduced in Example 10. 4 has state space {…, 1, 0, 1, …} and Markov chain p p p … 1 p 2 1 p 1 1 p 0 1 p 1 1 p 2 … 1 p Is state 0 recurrent? Sol： 61

Positive Recurrence and Null Recurrence Definition： A recurrent state i is positive recurrent if E[Tii] < ; otherwise, state i is null recurrent. Example 13. 9：In Example 13. 7, we found that state 0 is recurrent. Is state 0 positive recurrent or null recurrent? Sol： 1 0 1/2 2/3 1/2 1 1/3 3 2 1/4 3/4 4/5 4 … 1/5 62

Theorem 13. 10 For a communicating class of a Markov chain, one of the following must be true： (a)All states are transient. (b)All states are null recurrent. (c)All states are positive recurrent. 63

Example 13. 10 In a Markov chain of Example 13. 7 and 13. 9, is state 33 positive recurrent, null recurrent, or transient? Sol： 64

Stationary Probabilities of Infinite Chains Theorem 13. 11： For an irreducible, aperiodic, positive recurrent Markov chain with states {0, 1, …}, the limiting n-step transition probabilities are where are the unique state probabilities satisfying 65

Example 13. 11 For the stationary probabilities of the router buffer described in Example 13. 6. Make sure to identify for what values of p that the stationary 1 p probabilities exist. p p p Sol： … 1 0 2 1 p 1 p 66

Part III Markov Chains & Queueing Systems 10. Discrete-Time Markov Chains 11. Stationary Distributions & Limiting Probabilities 12. State Classification 13. Limiting Theorems For Markov Chains 14. Continuous-Time Markov Chains 67

14. Continuous-Time Markov Chains Definition： A continuous-time Markov chain {X(t)| t 0} is a continuous-time, discrete-value random process such that for an infinitesimal time step of size , Continuous-time Markov chain is closely related to the Poisson process. The time until the next transition is an exponential R. V. with parameter 68

Embedded Discrete-Time Markov Chain Definition： For a continuous-time Markov chain with transition rates qij and state i departure rates vi, the embedded discrete-time Markov chain has transition probabilities pij=qij / i for states i with i > 0 and pii = 1 for states i with i = 0. Definition： The Communicating Classes of a Continuous-Time Markov Chain are given by the communicating classes of its embedded discrete-time Markov chain. 69

Irreducible Continuous-Time Markov Chain Definition： A continuous-time Markov chain is irreducible if the embedded discrete-time Markov chain is irreducible. Definition： An irreducible continuous-time Markov chain is positive recurrent if for all states i, the time Tii to return to state i satisfying E[Tii] < . 70

Example 14. 1 In a continuous-time ON-OFF process, alternating OFF and ON (state 0 and 1) periods have independent exponential durations. The average ON period lasts 1/ seconds, while the average OFF period lasts 1/ seconds. Sketch the continuous-time Markov chain. Sol： 0 1 71

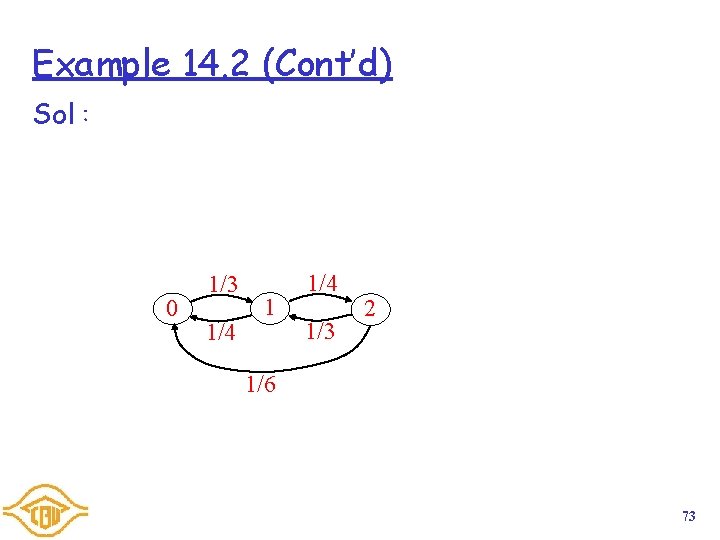
Example 14. 2 Air conditioner is in one of 3 states：OFF(0), Low (1), or High(2). The transitions from OFF to Low occur after an exponential with mean time 3 mins. The transitions from Low to OFF or High are equally likely and transitions out of the Low state occur at rate 0. 5 per min. When the system is in High state, it makes a transition to Low with probability 2/3 or to the OFF state with probability 1/3. The time spent in the high state is an exponential (1/2) R. V. Model this air conditioning system using a continuous-time Markov chain. 72

Example 14. 2 (Cont’d) Sol： 0 1/3 1/4 1/3 2 1/6 73

Theorem 14. 1 For a continuous-time Markov chain, the state probabilities pj(t) evolve according to the differential equations where Pf： 74

Theorem 14. 2 For an irreducible, positive recurrent continuoustime Markov chain, the state probabilities satisfying where the limiting state probabilities are the unique solution to Pf： j j qij Flow Conservation Law：ave. rate in = ave. rate out i 75

Example 14. 3 Calculate the limiting state probabilities for the ON-OFF system of Example 14. 1. 1 0 Sol： 76

Example 14. 4 Find the stationary distribution for the Markov chain describing the air conditioning system of Example 14. 2. 1/4 1/3 Sol： 1 0 2 1/3 1/4 1/6 77

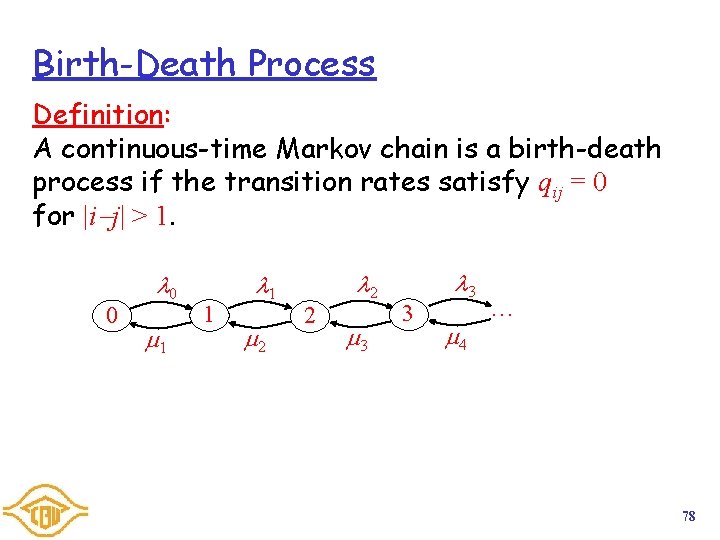
Birth-Death Process Definition: A continuous-time Markov chain is a birth-death process if the transition rates satisfy qij = 0 for |i j| > 1. 0 0 1 1 1 2 2 2 3 3 3 4 … 78

Theorem 14. 3 For a birth-death queue with arrival rate i and service rate i , the stationary probabilities pi satisfy Pf： 79

Theorem 14. 4 For a birth-death queue with arrival rate i and service rate i , let i = i / i+1. The limiting state probabilities, if they exist, are Pf： 80

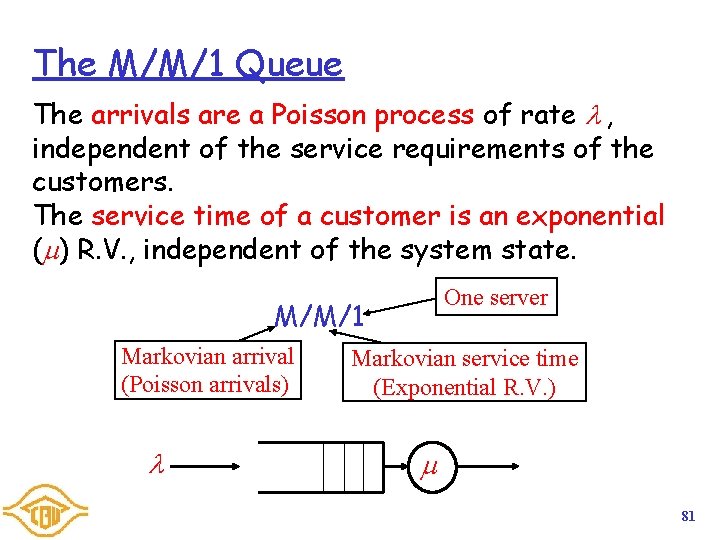
The M/M/1 Queue The arrivals are a Poisson process of rate , independent of the service requirements of the customers. The service time of a customer is an exponential ( ) R. V. , independent of the system state. One server M/M/1 Markovian arrival (Poisson arrivals) Markovian service time (Exponential R. V. ) 81

Theorem 14. 5 The M/M/1 queue with arrival rate > 0 and service rate , > , has limiting state probabilities, where = / . Pf： 82

Example 14. 5 Cars arrive at an isolated toll booth as a Poisson process with arrival rate = 0. 6 cars per minute. The service required by a customer is an exponential R. V. with expected value 1/ = 0. 3 minutes. What are the limiting state probabilities for N, the number of cars at the toll booth? What is the probability that the toll booth has zero cars some time in the distant future? Sol： 83