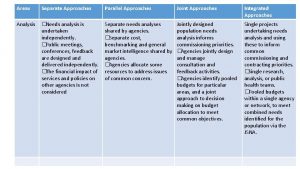
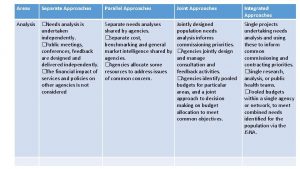
Traditional Approaches to Modeling and Analysis 1 Cognitive

Traditional Approaches to Modeling and Analysis 1 � © Cognitive Radio Technologies, 2007

Outline l Concepts: – – – l Models – – – 2 Dynamical Systems Model Fixed Points Optimality Convergence Stability Contraction Mappings Markov chains Standard Interference Function � © Cognitive Radio Technologies, 2007

Basic Model l Dynamical system – l Autonomous system – – Not a function of time OK for synchronous timing l Characteristic function l Evolution function – – – 3 A system whose change in state is a function of the current state and time First step in analysis of dynamical system Describes state as function of time & initial state. For simplicity while noting the relevant timing model � © Cognitive Radio Technologies, 2007

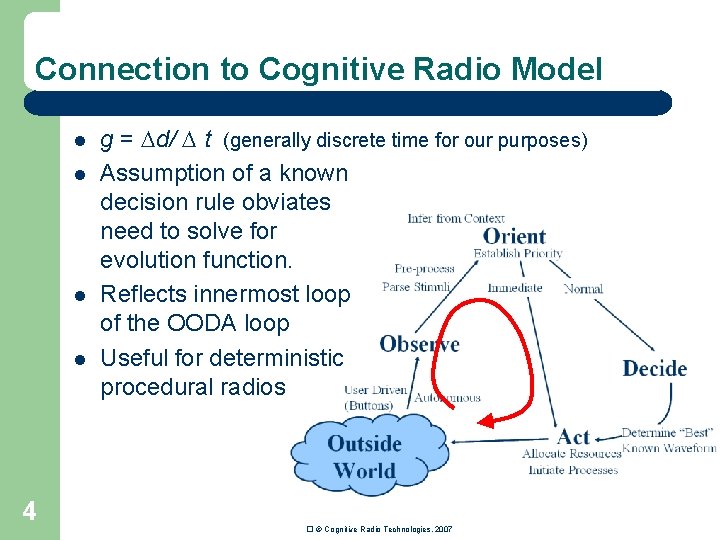
Connection to Cognitive Radio Model l l 4 g = d/ t (generally discrete time for our purposes) Assumption of a known decision rule obviates need to solve for evolution function. Reflects innermost loop of the OODA loop Useful for deterministic procedural radios � © Cognitive Radio Technologies, 2007

Example: ([Yates_95]) Power control applications l Defines a discrete time evolution function as a function of each radio’s observed SINR, j , each radio’s target SINR and the current transmit power l l l 5 Applications Fixed assignment - each mobile is assigned to a particular base station Minimum power assignment - each mobile is assigned to the base station in the network where its SINR is maximized Macro diversity - all base stations in the network combine the signals of the mobiles Limited diversity - a subset of the base stations combine the signals of the mobiles Multiple connection reception - the target SINR must be maintained at a number of base stations. � © Cognitive Radio Technologies, 2007

Applicable analysis models & techniques l Markov models – l Standard Interference Function – l l 6 Absorbing & ergodic chains Can be applied beyond power control Contraction mappings Lyapunov Stability � © Cognitive Radio Technologies, 2007

Differences between assumptions of dynamical system and CRN model l Goals of secondary importance – l Not appropriate for ontological radios – – l May not be a closed form expression for decision rule and thus no evolution function Really only know that radio will “intelligently” – work towards its goal Unwieldy for random procedural radios – 7 Technically not needed Possible to model as Markov chain, but requires empirical work or very detailed analysis to discover transition probabilities � © Cognitive Radio Technologies, 2007

Steady-states l l l Recall model of <N, A, {di}, T> which we characterize with the evolution function d Steady-state is a point where a*= d(a*) for all t t * Obvious solution: solve for fixed points of d. For non-cooperative radios, if a* is a fixed point under synchronous timing, then it is under the other three timings. Works well for convex action spaces – – l Not so well for finite spaces – 8 Not always guaranteed to exist Value of fixed point theorems Generally requires exhaustive search � © Cognitive Radio Technologies, 2007

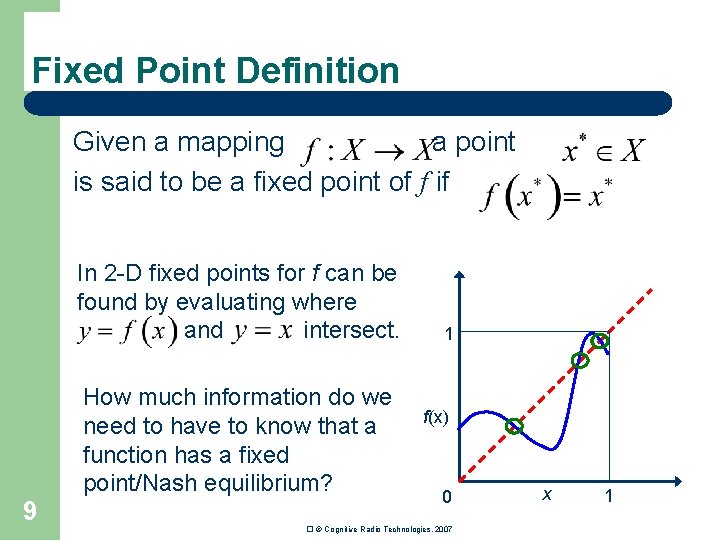
Fixed Point Definition Given a mapping a point is said to be a fixed point of f if In 2 -D fixed points for f can be found by evaluating where and intersect. How much information do we need to have to know that a function has a fixed point/Nash equilibrium? 9 1 f(x) 0 � © Cognitive Radio Technologies, 2007 x 1

Visualizing Fixed Point Existence l l l Consider continuous X compact, convex Fixed Point must exist 1 f(x) 0 10 � © Cognitive Radio Technologies, 2007 x 1

Convex Sets Definition Convex Set Let S n. S is said to be convex if for all x, y S, the point w = x + (1 - )y is in S for all [0, 1]. Equivalent expression A set S is convex if for all possible pairs of points, x, y, drawn from S the line segments joining x, y is also in S. Convex Not Convex y x 11 � © Cognitive Radio Technologies, 2007

Compact Sets Definition Compact Set A bounded set S is compact if there is no point x S such that the limit of a sequence formed entirely from elements in S is x. Equivalent – closed and bounded Compact sets Any closed finite interval [0, 1] Closed n-Ball 12 Closed Disk (A filled sphere) Non-compact sets (0, 1] [0, ) (Note, mathematically a disk is just a ball) � © Cognitive Radio Technologies, 2007

Continuous Function Definition Continuous Function A function f: X Y is continuous if for all x 0 X the following three conditions hold: f(x 0) Y Note being differentiable at x 0 implies continuity at x 0, but continuity does not imply differentiability 13 A continuous but not differentiable function � © Cognitive Radio Technologies, 2007

Visualizing Fixed Point Existence l l l 14 Consider continuous X not compact, convex or X compact, not convex Fixed point need not exist 1 f(x) 0 � © Cognitive Radio Technologies, 2007 x 1

Brouwer’s Fixed Point Theorem Let f : X X be a continuous function from a non-empty compact convex set X n, then there is some x* X such that f(x*) = x*. (Note originally written as f : B B where B = {x n : ||x|| 1} [the unit n-ball]) 15 � © Cognitive Radio Technologies, 2007

Visualizing Fixed Point Existence l l Consider f : X X as an upper semicontinuous correspondence X compact, convex 1 f(x) 0 16 � © Cognitive Radio Technologies, 2007 x 1

Kakutani’s Fixed Point Theorem l 17 Let f : X X be a upper semi-continuous convex valued correspondence from a nonempty compact convex set X n, then there is some x* X such that x* f(x*) � © Cognitive Radio Technologies, 2007

Example steady-state solution l 18 Consider Standard Interference Function � © Cognitive Radio Technologies, 2007

Optimality l l l In general we assume the existence of some design objective function J: A The desirableness of a network state, a, is the value of J(a). In general maximizers of J are unrelated to fixed points of d. Figure from Fig 2. 6 in I. Akbar, “Statistical Analysis of Wireless Systems Using Markov Models, ” Ph. D Dissertation, Virginia Tech, January 2007 19 � © Cognitive Radio Technologies, 2007

Identification of Optimality l 20 If J is differentiable, then optimal point must either lie on a boundary or be at a point where the gradient is the zero vector � © Cognitive Radio Technologies, 2007

Convergent Sequence 21 l A sequence {pn} in a Euclidean space X with point p X such that for every >0, there is an integer N such that n N implies d. X(pn, p)< l This can be equivalently written as or � © Cognitive Radio Technologies, 2007

Example Convergent Sequence l Given , choose N=1/ , p=0 0 1 Establish convergence by applying definition Necessitates knowledge of p. 22 � © Cognitive Radio Technologies, 2007

Convergent Sequence Properties 23 � © Cognitive Radio Technologies, 2007

Cauchy Sequence l 24 A sequence {pn} in a metric space X such that for every >0, there is an integer N such that if � © Cognitive Radio Technologies, 2007

Example Cauchy Sequence l Given , choose N=2/ , p=0 0 1 Establish convergence by applying definition No need to know p In k, every Cauchy sequence converges, and every convergent sequence is Cauchy 25 � © Cognitive Radio Technologies, 2007

Monotonic Sequences 26 l A sequence {sn} is monotonically increasing if. l A sequence {sn} is monotonically decreasing if l (Note: some authors use the inclusion of the equals condition to define a sequence to be respectively monotonically nondecreasing or monotonically nonincreasing. ). A sequence which is either monotonically increasing or monotonically decreasing is said to be monotonic. � © Cognitive Radio Technologies, 2007

Convergent Monotonic Sequences l l 27 Suppose is a monotonic in X. Then converges if X is bounded. Note that also converges if X is compact. � © Cognitive Radio Technologies, 2007

Showing convergence with nonlinear programming Left unanswered: where does come from? 28 � © Cognitive Radio Technologies, 2007

Stability 29 Stable, but not attractive Attractive, but not stable � © Cognitive Radio Technologies, 2007

Lyapunov’s Direct Method 30 Left unanswered: where does L come from? � © Cognitive Radio Technologies, 2007

Comments on analysis l l l 31 We just covered some very general techniques for showing that a system has a fixed point (steadystate), converges, and is stable. Could apply these to every problem independently, but can sometimes be painful (and nonobvious – where does Lyapunov function come from, convergence assumes we already know a fixed point) My preferred approach is to analyze general models and then show that particular problems satisfy conditions of one of the general models. � © Cognitive Radio Technologies, 2007

Analysis models appropriate for dynamical systems l Contraction Mappings – – – Identifiable unique steady-state Everywhere convergent, bound for convergence rate Lyapunov stable ( = ) l – Forms a pseudo-contraction mapping Can be applied beyond power control Markov Chains (Ergodic and Absorbing) – 32 General Convergence Theorem (Bertsekas) provides convergence for asynchronous timing if contraction mapping under synchronous timing Standard Interference Function – l Lyapunov function = distance to fixed point Also useful in game analysis � © Cognitive Radio Technologies, 2007

Contraction Mappings l l 33 Every contraction is a pseudocontraction Every pseudo-contraction has a fixed point Every pseudo-contraction converges at a rate of Every pseudo-contraction is globally asymptotically stable – Lyapunov function is distance to the fixed point) � © Cognitive Radio Technologies, 2007 A Pseudo-contraction which is not a contraction

General Convergence Theorem l 34 A synchronous contraction mapping also converges asynchronously � © Cognitive Radio Technologies, 2007

Standard Interference Function l l Conditions Suppose d: A A and d satisfies: – – – l d is a pseudo-contraction mapping [Berggren] under synchronous timing – – 35 Positivity: d(a)>0 Monotonicity: If a 1 a 2, then d(a 1) d(a 2) Scalability: For all >1, d(a)>d( a) Implies synchronous and asynchronous convergence Implies stability R. Yates, “A Framework for Uplink Power Control in Cellular Radio Systems, ” IEEE JSAC. , Vol. 13, No 7, Sep. 1995, pp. 1341 -1347. F. Berggren, “Power Control, Transmission Rate Control and Scheduling in Cellular Radio Systems, ” � © Cognitive Radio Technologies, 2007 2001. Ph. D Dissertation Royal Institute of Technology, Stockholm, Sweden, May,

Yates’ power control applications l Target SINR algorithms l Fixed assignment - each mobile is assigned to a particular base station Minimum power assignment - each mobile is assigned to the base station in the network where its SINR is maximized Macro diversity - all base stations in the network combine the signals of the mobiles Limited diversity - a subset of the base stations combine the signals of the mobiles Multiple connection reception - the target SINR must be maintained at a number of base stations. l l l 36 l � © Cognitive Radio Technologies, 2007

Example steady-state solution l 37 Consider Standard Interference Function � © Cognitive Radio Technologies, 2007

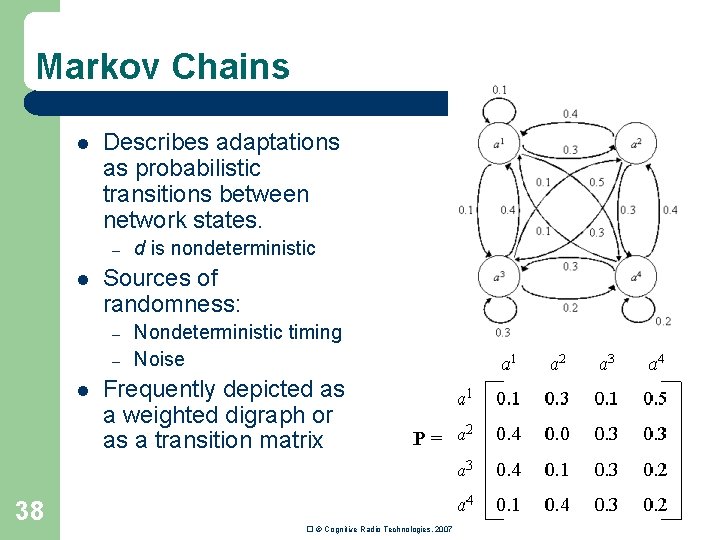
Markov Chains l Describes adaptations as probabilistic transitions between network states. – l Sources of randomness: – – l 38 d is nondeterministic Nondeterministic timing Noise Frequently depicted as a weighted digraph or as a transition matrix � © Cognitive Radio Technologies, 2007

General Insights ([Stewart_94]) l Probability of occupying a state after two iterations. – – l Consider Pk. – 39 Form PP. Now entry pmn in the mth row and nth column of PP represents the probability that system is in state an two iterations after being in state am. Then entry pmn in the mth row and nth column of represents the probability that system is in state an two iterations after being in state am. � © Cognitive Radio Technologies, 2007

Steady-states of Markov chains l May be inaccurate to consider a Markov chain to have a fixed point – l Stationary Distribution – l A probability distribution such that *T P = *T is said to be a stationary distribution for the Markov chain defined by P. Limiting distribution – 40 Actually ok for absorbing Markov chains Given initial distribution 0 and transition matrix P, the limiting distribution is the distribution that results from evaluating � © Cognitive Radio Technologies, 2007

Ergodic Markov Chain l l [Stewart_94] states that a Markov chain is ergodic if it is a Markov chain if it is a) irreducible, b) positive recurrent, and c) aperiodic. Easier to identify rule: – l 41 For some k Pk has only nonzero entries (Convergence, steady-state) If ergodic, then chain has a unique limiting stationary distribution. � © Cognitive Radio Technologies, 2007

Shortcomings in traditional techniques l l Fixed point theorems provide little insight into convergence or stability Lyapunov functions hard to identify Contraction mappings rarely encountered Doesn’t address nondeterministic algorithms – l l l 42 Genetic algorithms Analyze one algorithm at a time – little insight into related algorithms Not very useful for finite action spaces No help if all you have is the cognitive radios’ goal and actions � © Cognitive Radio Technologies, 2007

Absorbing Markov Chains l Absorbing state – l Given a Markov chain with transition matrix P, a state am is said to be an absorbing state if pmm=1. Absorbing Markov Chain – A Markov chain is said to be an absorbing Markov chain if l l 43 a 0 it has at least one absorbing state and from every state in the Markov chain there exists a sequence of state transitions with nonzero probability that leads to an absorbing state. These nonabsorbing states are called transient states. a 1 a 2 a 3 � © Cognitive Radio Technologies, 2007 a 4 a 5

Absorbing Markov Chain Insights ([Kemeny_60] ) l Canonical Form l Fundamental Matrix l Expected number of times that the system will pass through state am given that the system starts in state ak. – l (Convergence Rate) Expected number of iterations before the system ends in an absorbing state starting in state am is given by tm where 1 is a ones vector – l 44 nkm t=N 1 (Final distribution) Probability of ending up in absorbing state am given that the system started in ak is bkm where � © Cognitive Radio Technologies, 2007

Two-Channel DFS Decision Rule Goal Timing Random timer set to go off with probability p=0. 5 at each iteration 45 � © Cognitive Radio Technologies, 2007

Analysis Models 46 � © Cognitive Radio Technologies, 2007

Model Steady States 47 � © Cognitive Radio Technologies, 2007

Model Convergence 48 � © Cognitive Radio Technologies, 2007

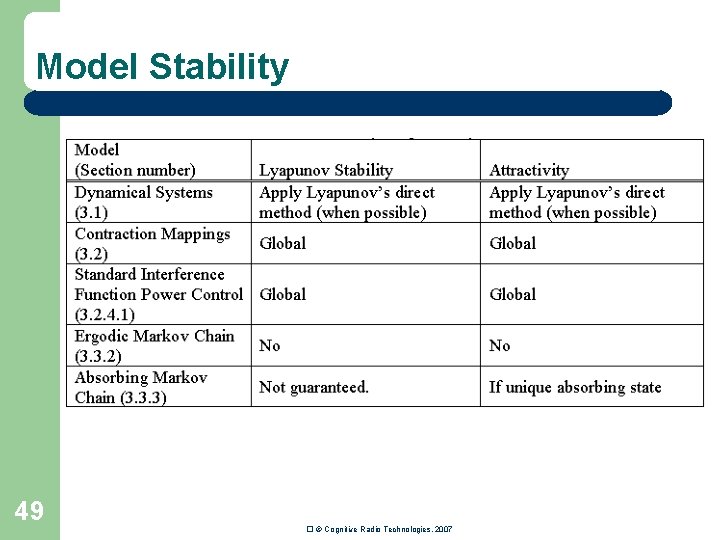
Model Stability 49 � © Cognitive Radio Technologies, 2007

Shortcomings in “traditional” techniques l l Fixed point theorems provide little insight into convergence or stability Lyapunov functions hard to identify Contraction mappings rarely encountered Doesn’t address nondeterministic algorithms – l l 50 Genetic algorithms Not very useful for finite action spaces No help if all you have is the cognitive radios’ goal and actions � © Cognitive Radio Technologies, 2007

Comments l No unified method for analyzing cognitive radio interactions – l l 51 Random collection of methods for different problems Perhaps a bit of a stretch to call it “traditional” with respect to cognitive radios Is not suitable for analyzing radios with � © Cognitive Radio Technologies, 2007