G 12 Management Science Markov Chains Outline Classification













































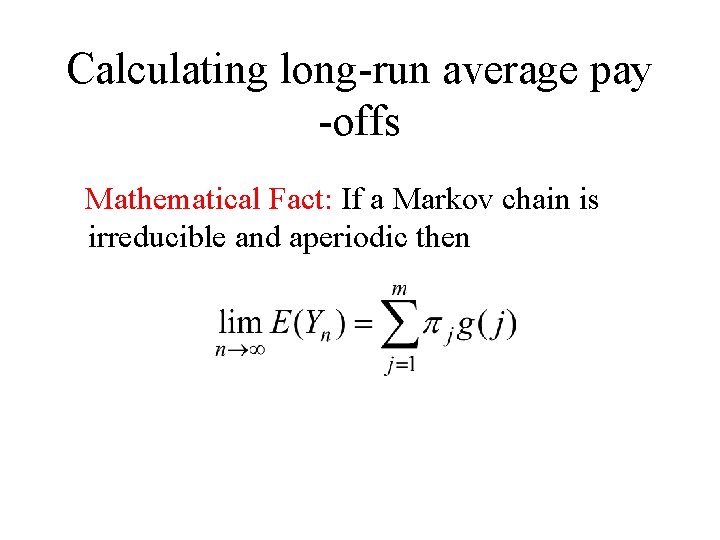


- Slides: 53

G 12: Management Science Markov Chains

Outline • Classification of stochastic processes • • Markov processes and Markov chains Transition probabilities Transition networks and classes of states First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

Analysing Uncertainty • Computer Models of Uncertainty: – Building blocks: Random number generators – Simulation Models • Static (product launch example) • Dynamic (inventory example and queuing models) • Mathematical Models of Uncertainty: – Building blocks: Random Variables – Mathematical Models • Static: Functions of Random Variables • Dynamic: Stochastic (Random) Processes

Stochastic Processes • Collection of random variables Xt, t in T – Xt’s are typically statistically dependent • State space: set of possible values of Xt’s – State space is the same for all Xt’s – Discrete space: Xt’s are discrete RVs – Continuous space: Xt’s are continuous RVs • Time domain: – Discrete time: T={0, 1, 2, 3, …} – Continuous time: T is an interval (possibly unbounded)

Examples from Queuing Theory • Discrete time, discrete space – Ln: queue length upon arrival of nth customer • Discrete time, continuous space – Wn: waiting time of nth customer • Continuous time, discrete space – Lt: queue length at time t • Continuous time, continuous space – Wt: waiting time for a customer arriving at time t

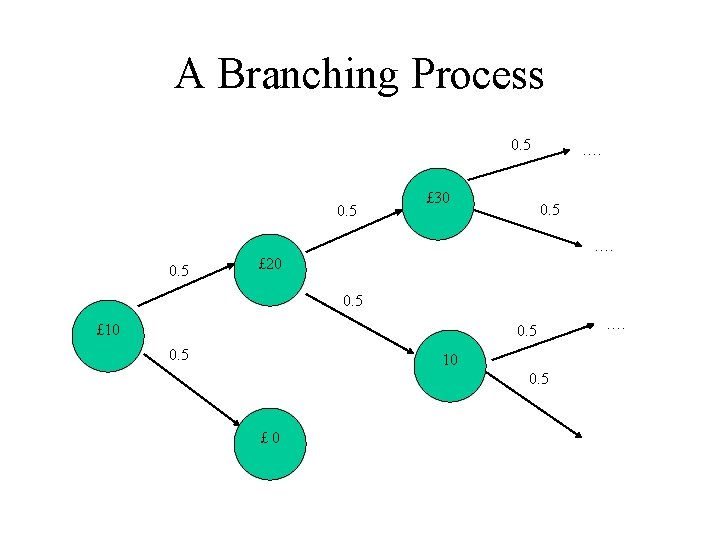
A gambling example • Game: Flip a coin. You win £ 10 if coin shows head and loose £ 10 otherwise • You start with £ 10 and you keep playing until you are broke • Typical questions – What is the expected amount of money after t flips? – What is the expected length of the game?

A Branching Process 0. 5 £ 30 …. 0. 5 £ 20 0. 5 £ 10 0. 5 £ 0 ….

Discrete Time - Discrete State Stochastic Processes • • Xt: Amount of money you own after t flips Stochastic Process: X 1, X 2, X 3, … Each Xt has its own probability distribution The RVs are dependent: the probability of having £ k after t flips depends on what you had after t’ (<t) flips – Knowing Xt’ changes the probability distribution of Xt (conditional probability)

Outline • Classification of stochastic processes • Markov processes and Markov chains • Transition probabilities • Transition networks and classes of states • First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

Markovian Property • Waiting time at time t depends on waiting time at times t’<t – Knowing waiting time at some time t’<t changes the probability distribution of waiting time at time t (Conditional probability) – Knowledge of history generally improves probability distribution (smaller variance) • Generally: The distribution of states at time t depends on the whole history of the process – Knowing states of the system at times t 1, …tn<t changes the distribution of states at time t • Markov property: The distribution of states at time t, given the states at times t 1<…<tn<t is the same as the distribution of states at time t, given only knowledge of the state at time tn. – The distribution depends only on the last observed state – Knowledge about earlier states does not improve probability distribution

Discrete time, discrete space • P(Xt+1= j | X 0=i 0, …, Xt=it) = P(Xt+1= j | Xt=it) • In words: The probabilities that govern a transition from state i at time t to state j at time t+1 only depend on the state i at time t and not on the states the process was in before time t

Transition Probabilities • The transition probabilites are P(Xt+1= j | Xt=i) • Transition probabilities are called stationary if P(Xt+1= j | Xt=i) = P(X 1= j | X 0=i) • If there are only finitely many possible states of the RVs Xt then the stationary transition probabilities are conveniently stored in a transition matrix Pij= P(X 1= j | X 0=i) • Find the transition matrix for our first example if the game ends if the gambler is either broke or has earned £ 30

Markov Chains • Stochastic process with a finite number, say n, possible states that has the Markov property • Transitions between states in discrete time steps • MC is completely characterised by transition probabilities Pij from state i to state j are stored in an n x n transition matrix P – Rows of transition matrix sum up to 1. Such a matrix is called a stochastic matrix • Initial distribution of states is given by an initial probability vector p(0)=(p 1(0), …, pn(0)) • We are interested in the change of the probability distribution of the states over time

Markov Chains as Modelling Templates • Lawn mower example: – Weekly demand D for lawn mowers has distribution P(D=0)=1/3, P(D=1)=1/2, P(D=2)=1/6 – Mowers can be ordered at the end of each week and are delivered right at the beginning of the next week – Inventory policy: Order two new mowers if stock is empty at the end of the week – Currently (beginning of week 0) there are two lawn mowers in stock • Determine the transition matrix

Market Shares • Two software packages, B and C, enter a market that has so far been dominated by software A • C is more powerful than B which is more powerful than A • C is a big departure from A, while B has some elements in common with both A and C • Market research shows that about 65% of A-users are satisfied with the product and won’t change over the next three months • 30% of A-users are willing to move to B, 5% are willing to move to C….

Transition Matrix • All transition probabilities over the next three months can be found in the following transition matrix • What are the approximate market shares going to be?

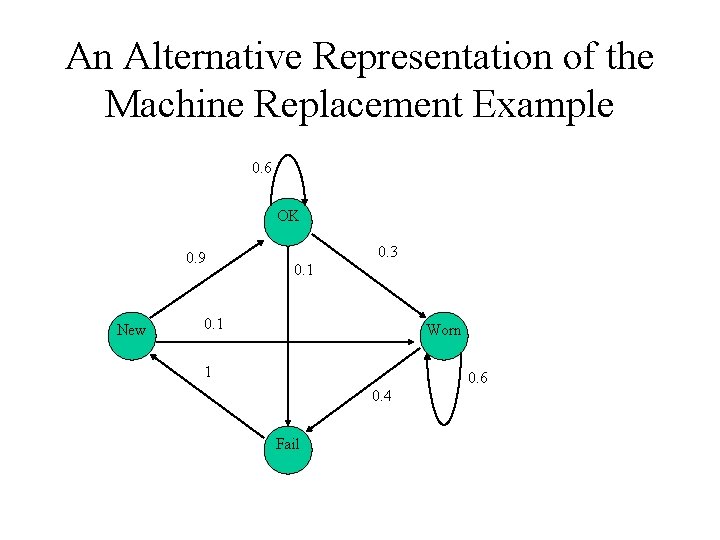
Machine Replacement • Many identical machines are used in a manufacturing environment • They deteriorate over time with the following monthly transition probabilities:

Outline • Classification of stochastic processes • Markov processes and Markov chains • Transition probabilities • Transition networks and classes of states • First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

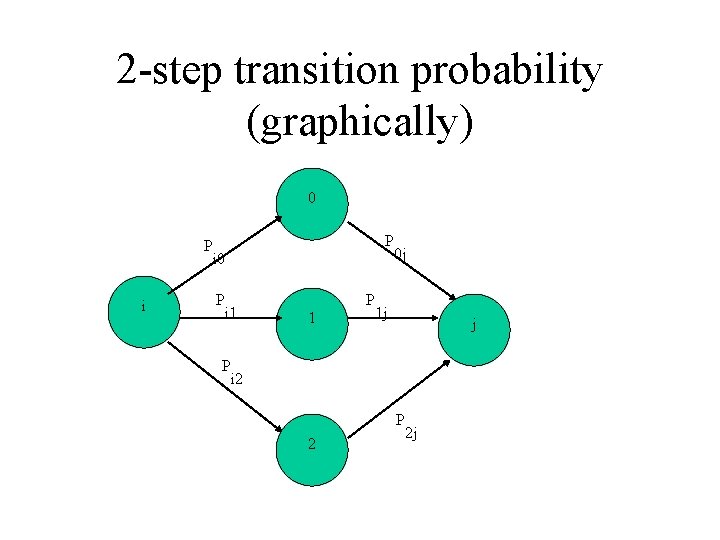
2 -step transition probability (graphically) 0 P i 1 P P 1 0 j 1 j j i 2 P 2 2 j

2 -step transition probabilities (formally)

Chapman-Kolmogorov Equations • Similarly, one shows that n-step transition probabilities Pij(n)=P(Xn=j | X 0=i) obey the following law (for arbitrary m<n: ) • The n-step transition probability matrix P(n) is the n-th power of the 1 -step TPM P: P(n) =Pn=P…P (n times)

Example see spreadsheet Markov. xls

Distribution of Xn • Given – – • • Markov chain with m states (1, …, m) and transition matrix P Probability vector for initial state (t=0): p(0)=(p 1(0), …, pm(0)) What is the probability that the process is in state i after n transitions? Bayes’ formula: P(Xn=i)=P(Xn=i¦X 0=1)p 1(0)+…+P(Xn=i¦X 0=m)pm(0) • • Probability vector for Xn: p(n)= p(0)Pn Iteratively: p(n+1)= p(n)P • Open spreadsheet Markov. xls for lawn mower, market share, and machine replacement examples

Outline • Classification of stochastic processes • Markov processes and Markov chains • Transition probabilities • Transition networks and classes of states • First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

An Alternative Representation of the Machine Replacement Example 0. 6 OK 0. 9 New 0. 3 0. 1 Worn 1 0. 6 0. 4 Fail

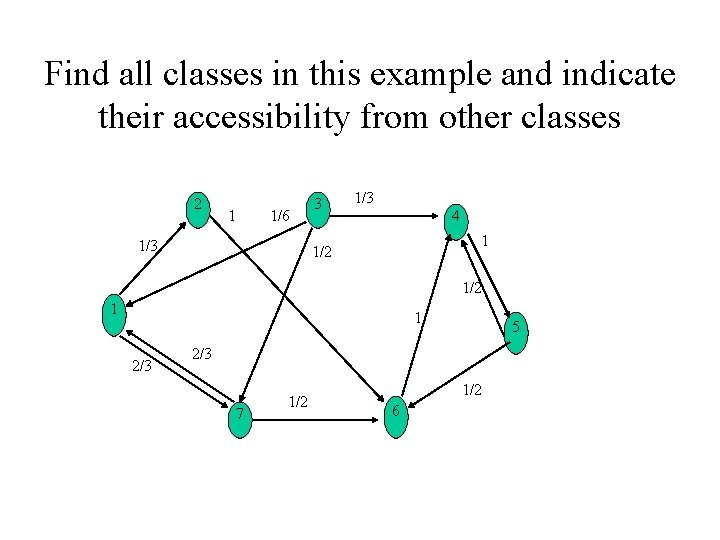
The transition network • The nodes of the network correspond to the states • There is an arc from node i to node j if Pij > 0 and this arc has an associated value Pij • State i is accessible from state j if there is a path in the network from node i to node j • A stochastic matrix is said to be irreducible if each state is accessible from each other state

Classes of States • State i and j communicate if i is accessible from j and j is accessible from i • Communicating states form classes • A class is called absorbing if it is not possible to escape from it • A class A is said to be accessible from a class B if each state in A is accessible from each state in B – Equivalently: …if some state in A is accessible from some state in B

Find all classes in this example and indicate their accessibility from other classes 2 1 1/6 1/3 3 1/3 4 1 1/2 1 1 2/3 5 2/3 7 1/2 6

Return to Gambling Example • • • Draw the transition network Find all classes Is the Markov chain irreducible? Indicate the accessibility of the classes Is there an absorbing class?

Outline • • Classification of stochastic processes Markov processes and Markov chains Transition probabilities Transition networks and classes of states • First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

First passage times • The first passage time from state i to state j is the number of transitions until the process hits state j if it starts at state i • First passage time is a random variable • Define fij(k) = probability that the first passage from state i to state j occurs after k transitions

Calculating fij(k) • Use Bayes’ formula P(A)=P(A|B 1)P(B 1)+…+ P(A|Bn)P(Bn) • Event A: starting from sate i the process is in state j after n transitions (P(A)=Pij(n)) • Event Bk: first passage from i to j happens after k transitions

Calculating fij(k) (cont. ) Bayes’ formula gives: This results in the recursion formula:

Alternative: Simulation • Do a number of simulations, starting from state i and stopping when you have reached state j • Estimate fij(k) = Percentage of runs of length k • BUT: This may take a long time if you want to do this for all state combinations (i, j) and many k’s

Expected first passage time • If Xij = time of first passage from i to j then E(Xij)=fij(1)+2 fij(2)+3 fij(3)+…. • Use conditional expectation formula E(Xij)=E(Xij|B 1)P(B 1)+…+ E(Xij|Bn)P(Bn) • Event Bk: first transition goes from i to k • Notice – E(Xij |Bj)=1 and E(Xij|Bk)=1+E(Xkj)

Hence

Example

Outline • • • Classification of stochastic processes Markov processes and Markov chains Transition probabilities Transition networks and classes of states First passage time probabilities and expected first passage time • Long-term behaviour and steady state distribution

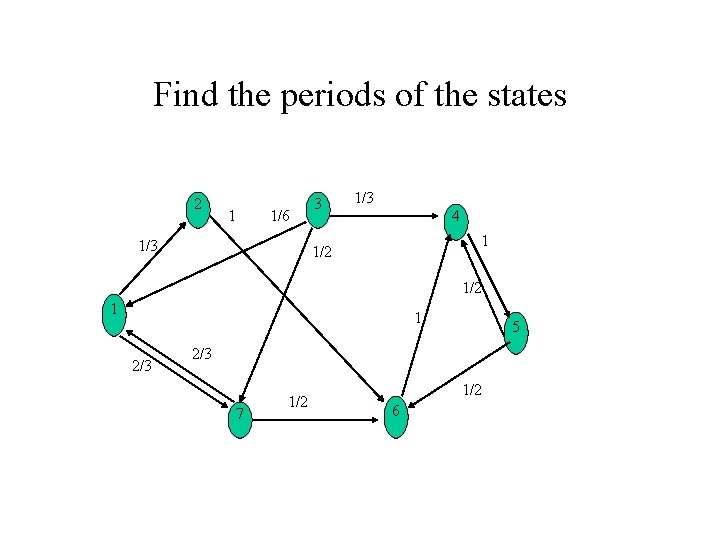
Long term behaviour • We are interested in distribution of Xn as n tends to infinity: lim p(n)=lim p(0)P(n)= p(0) lim P(n) • If lim P(n) exists then P is called • The limit may not exist, though: • See Markov. xls • Problem: Process has periodic behaviour – Process can only recur to state i after t, 2 t, 3 t, … steps – There exists t: if n Not in {t, 2 t, 3 t} then Pii(n) = 0 • Period of a state i: maximal such t

Find the periods of the states 2 1 1/6 1/3 3 1/3 4 1 1/2 1 1 2/3 5 2/3 7 1/2 6

Aperiodicity • A state with period 1 is called aperiodic • State i is aperiodic if and only if there exists N such that Pii(N) > 0 and Pii(N+1) > 0 • The Chapman-Kolmogorov Equations therefore imply that Pii(n)>0 for every n>=N • Aperiodicity is a class property, i. e. if one state in a class is aperiodic, then so are all others

Regular matrices • A stochastic matrix P is called regular if there exists a number n such that all entries of Pn are positive • A Markov chain with a regular transition matrix is aperiodic (i. e. all states are aperiodic) and irreducible (i. e. all states communicate)

Back to long-term behaviour • Mathematical Fact: If a Markov chain is irreducible and aperiodic then it is ergodic, i. e. , all limits exist

Finding the long term probabilities • Mathematical Result: If a Markov chain is irreducible and aperiodic then all rows of its long term transition probability matrix are identical to the unique solution p=(p 1, …, pm) of the equations

However, . . . • …the latter system is of the form p. P=p, p 1+…+pm=1 and has m+1 equations and m unknowns – It has a solution because P is a stochastic matrix and therefore has 1 as an eigenvalue (with eigenvector x=(1, …, 1)). Hence p is just a left eigenvector of P to the eigenvalue 1 and the additional equation normalizes the eigenvector • Calculation: solve the system without the first equation - then check first equation

Example • Find the steady state probabilities for • Solution: (p 1, p 2)=(0. 6, 0. 4)

Steady state probabilities • The probability vector p with p. P=p and p 1+. . +pm=1 is called the steady state (or stationary) probability distribution of the Markov chain • A Markov chain does not necessarily have a steady state distribution • Mathematical result: an irreducible Markov chain has a steady state distribution

Tending towards steady state • If we start with the steady state distribution the probability distribution of the states does not change over time • More importantly: If the Markov chain is irreducible and aperiodic then, independently of the initial distribution, the distribution of states gets closer and closer to the steady state distribution • Illustration: see spreadsheet Markov. xls

More on steady state distributions • pj can be interpreted as the long-run proportion of time the process is in state j • Alternatively: pj=1/E(Xjj) where Xjj is the time of the first recurrence to j – E. g. if the expected recurrence time to state j is 2 transitions then, on the long run, the process will be in state j after every 1 out of two transitions, i. e. 1/2 of the time

Average Payoff Per Unit Time • Setting: If process hits state i, a payoff of g(i) is realized (costs = negative payoffs) • Average payoff period after n transitions Yn=(g(X 1)+…+g(Xn))/n • Long-run expected average payoff per time period: lim E(Yn) as n tends to infinity
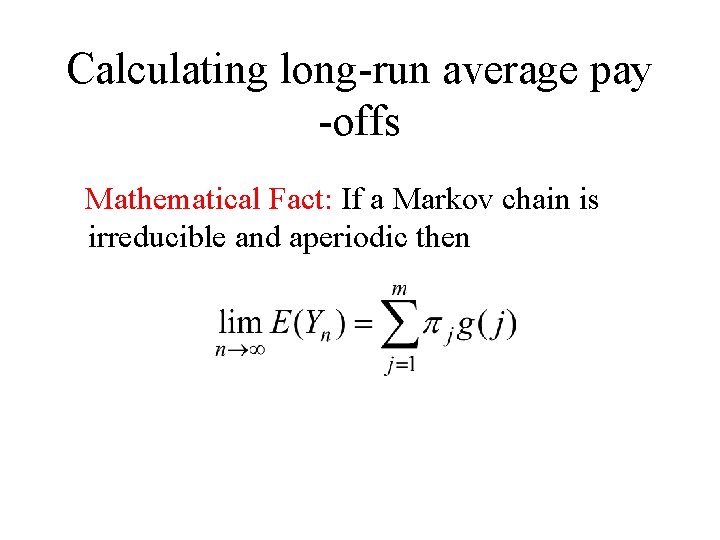
Calculating long-run average pay -offs Mathematical Fact: If a Markov chain is irreducible and aperiodic then

Example A transition takes place every week. A weekly cost of £ 1 has to be payed if the process is in state 1, while a weekly profit of £ 1 is obtained if the process is in state 1. Find the average payoff per week. (Solution: £ -0. 2 per week)

Key Learning Points • Markov chains are a template for the analysis of systems with finitely many states where random transitions between states happen at discrete points in time • We have seen how to calculate n-step transition probabilities, first passage time probabilities and expected first passage times • We have discussed steady state behaviour of a Markov chain and how to calculate steady state distributions