5 0 Discretetime Fourier Transform 5 1 Discretetime






![From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-10.jpg)
![From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-11.jpg)







![From Periodic to Aperiodic l Convergence Issue given x[n] – No convergence issue since From Periodic to Aperiodic l Convergence Issue given x[n] – No convergence issue since](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-19.jpg)




![From Periodic to Aperiodic l For Periodic Signals – Unified Framework – Given x[n] From Periodic to Aperiodic l For Periodic Signals – Unified Framework – Given x[n]](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-26.jpg)




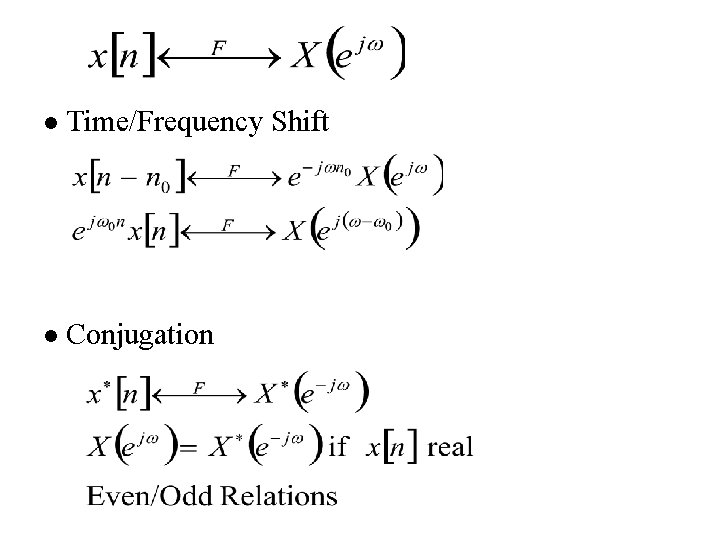

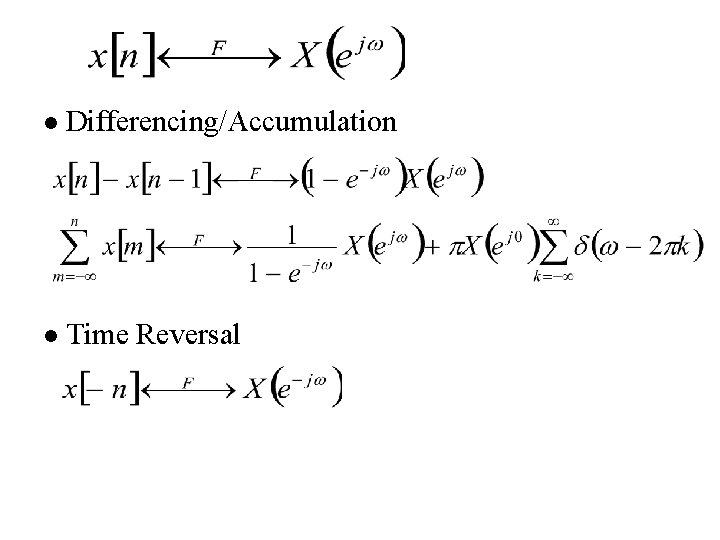









![l Vector Space Interpretation {x[n], aperiodic defined on -∞ < n < ∞}=V is l Vector Space Interpretation {x[n], aperiodic defined on -∞ < n < ∞}=V is](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-51.jpg)





![<B> Fourier Series for Discrete-time Periodic Signals (Synthesis) (3. 94) (Analysis) (3. 95) -x[n] <B> Fourier Series for Discrete-time Periodic Signals (Synthesis) (3. 94) (Analysis) (3. 95) -x[n]](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-59.jpg)











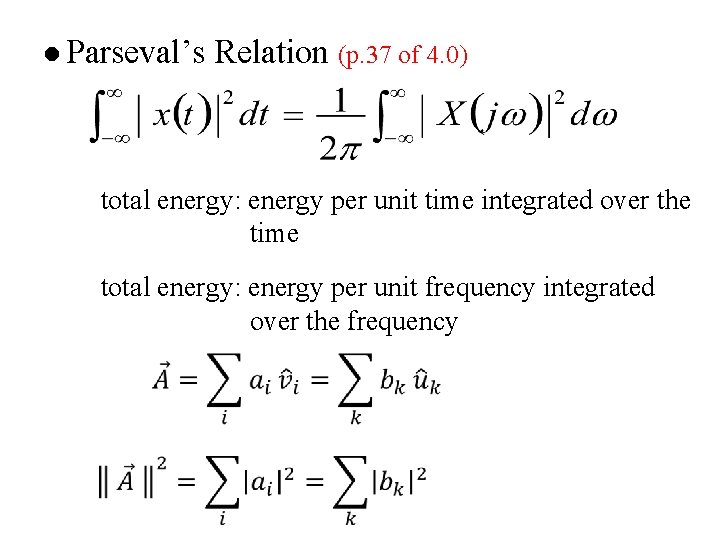











- Slides: 99

5. 0 Discrete-time Fourier Transform 5. 1 Discrete-time Fourier Transform Representation for discrete-time signals Chapters 3, 4, 5 Chap 3 Periodic Fourier Series Chap 4 Aperiodic Fourier Transform Chap 5 Aperiodic Fourier Transform

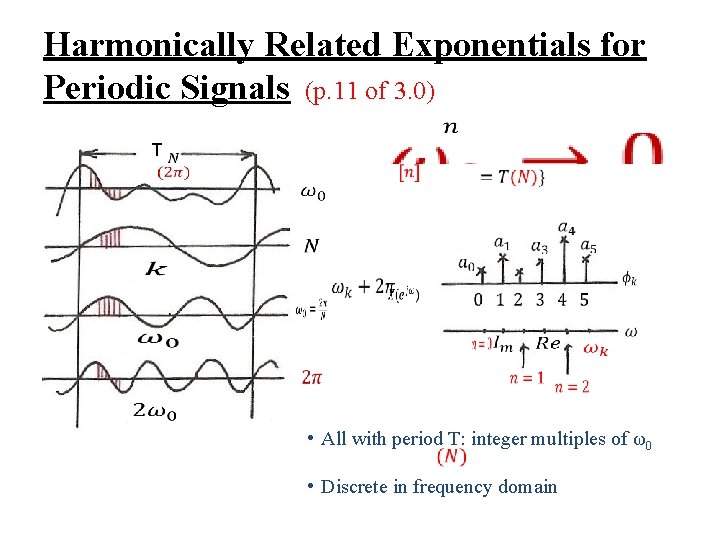
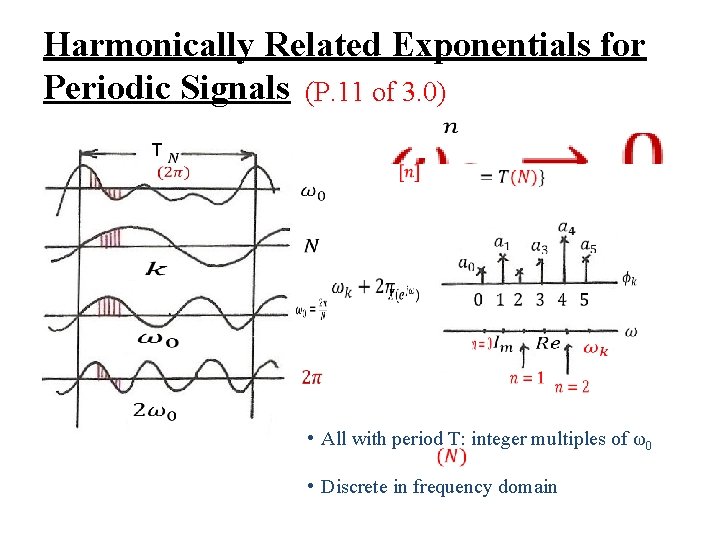
Harmonically Related Exponentials for Periodic Signals (p. 11 of 3. 0) T • All with period T: integer multiples of ω0 • Discrete in frequency domain

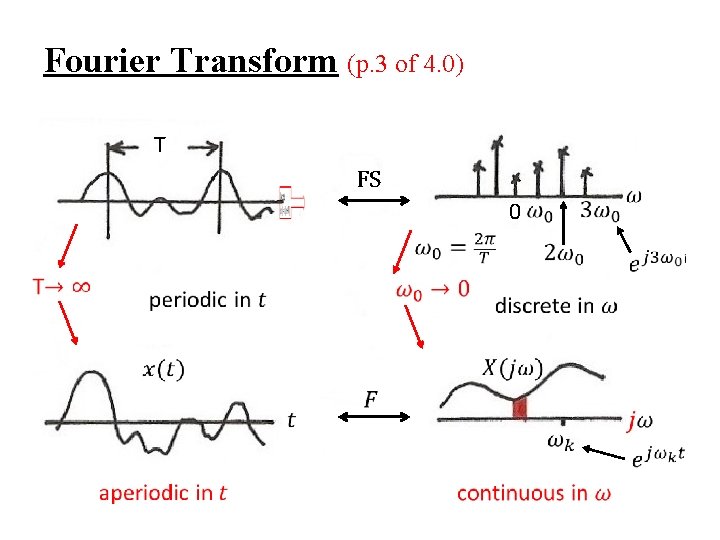
Fourier Transform (p. 3 of 4. 0) T FS 0

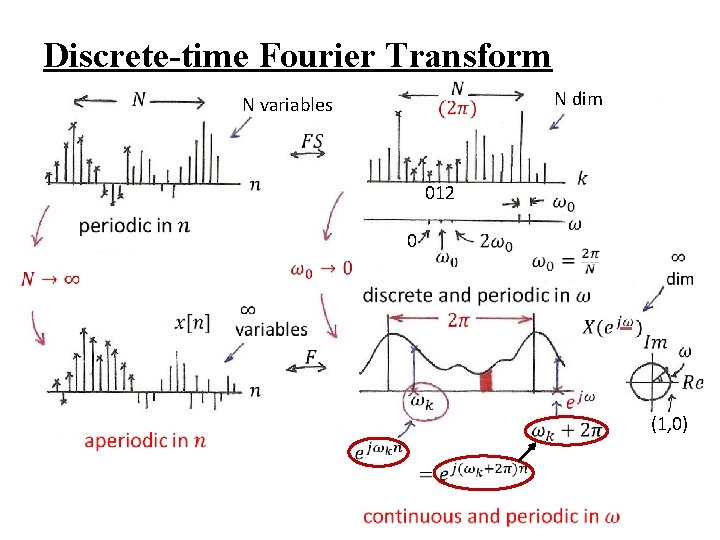
Discrete-time Fourier Transform N dim N variables 012 0 (1, 0)





![From Periodic to Aperiodic l Considering xn xn0 for n N 2 or From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-10.jpg)
From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or n < -N 1 – Construct
![From Periodic to Aperiodic l Considering xn xn0 for n N 2 or From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-11.jpg)
From Periodic to Aperiodic l Considering x[n], x[n]=0 for n > N 2 or n < -N 1 – Fourier series for – Defining envelope of

– As signal, time domain, Inverse Discrete-time Fourier Transform spectrum, frequency domain Discrete-time Fourier Transform – Similar format to all Fourier analysis representations previously discussed

(p. 10 of 4. 0) spectrum, frequency domain Fourier Transform signal, time domain Inverse Fourier Transform pair, different expressions very similar format to Fourier Series for periodic signals

l Note: X(ejω) is continuous and periodic with period 2 Integration over 2 only Frequency domain spectrum is continuous and periodic, while time domain signal is discrete-time and aperiodic Frequencies around ω=0 or 2 are lowfrequencies, while those around ω= are highfrequencies, etc. See Fig. 5. 3, p. 362 of text For Examples see Fig. 5. 5, 5. 6, p. 364, 365 of text




![From Periodic to Aperiodic l Convergence Issue given xn No convergence issue since From Periodic to Aperiodic l Convergence Issue given x[n] – No convergence issue since](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-19.jpg)
From Periodic to Aperiodic l Convergence Issue given x[n] – No convergence issue since the integration is over an finite interval – No Gibbs phenomenon See Fig. 5. 7, p. 368 of text




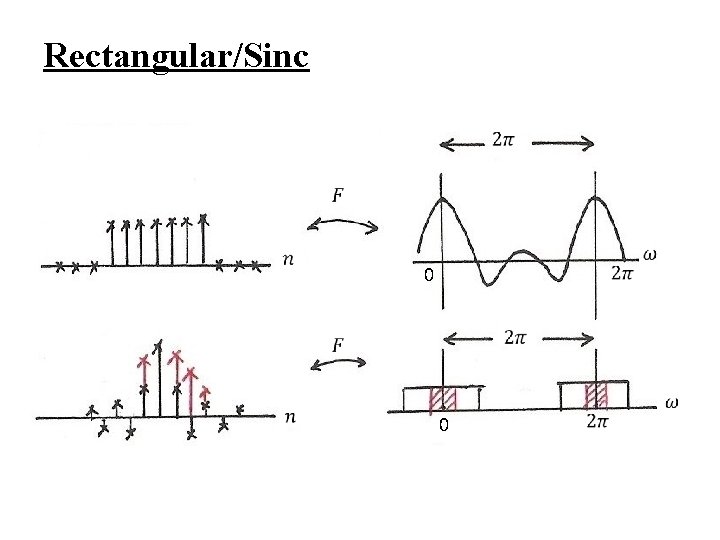
Rectangular/Sinc 0 0

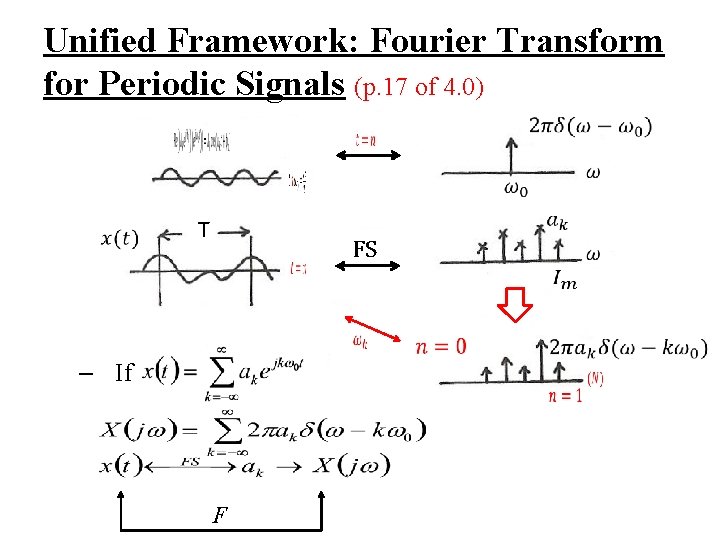
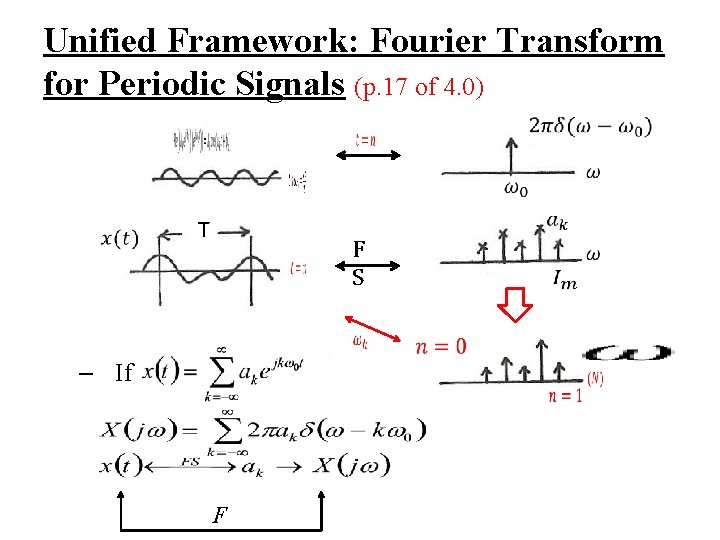
l Fourier Transform for Periodic Signals – Unified Framework (p. 16 of 4. 0) – Given x(t) (easy in one way)

Unified Framework: Fourier Transform for Periodic Signals (p. 17 of 4. 0) T FS – If F
![From Periodic to Aperiodic l For Periodic Signals Unified Framework Given xn From Periodic to Aperiodic l For Periodic Signals – Unified Framework – Given x[n]](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-26.jpg)
From Periodic to Aperiodic l For Periodic Signals – Unified Framework – Given x[n] See Fig. 5. 8, p. 369 of text


From Periodic to Aperiodic l For Periodic Signals – Unified Framework – If See Fig. 5. 9, p. 370 of text


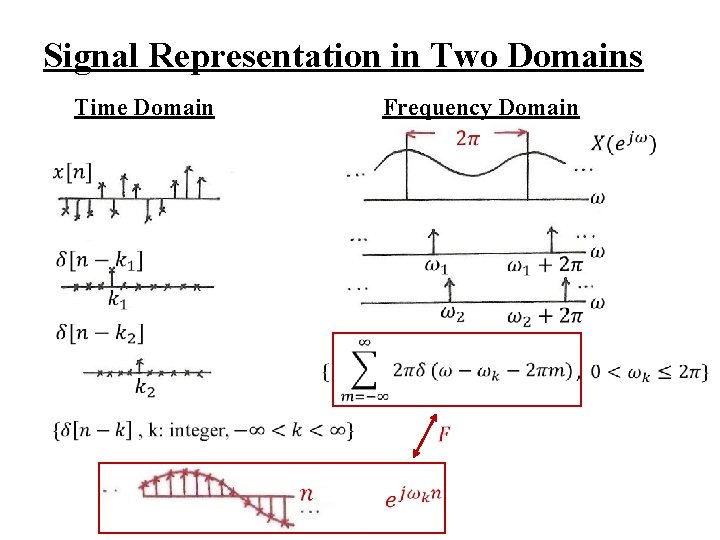
Signal Representation in Two Domains Time Domain Frequency Domain

5. 2 Properties of Discrete-time Fourier Transform l Periodicity l Linearity
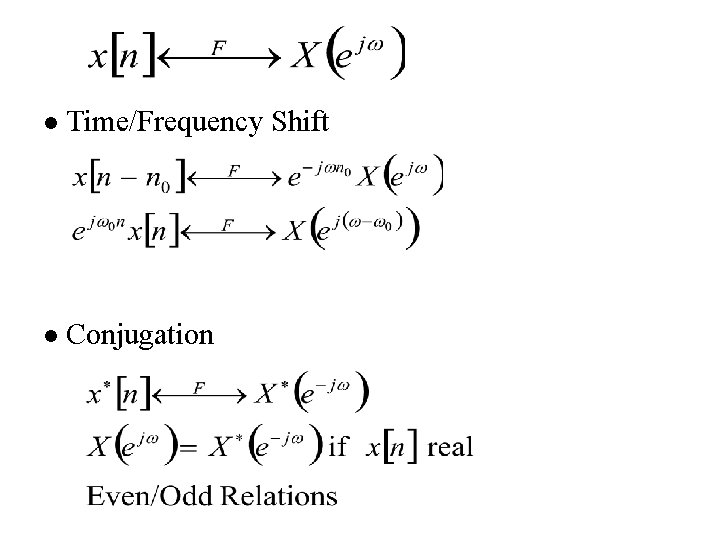
l Time/Frequency Shift l Conjugation

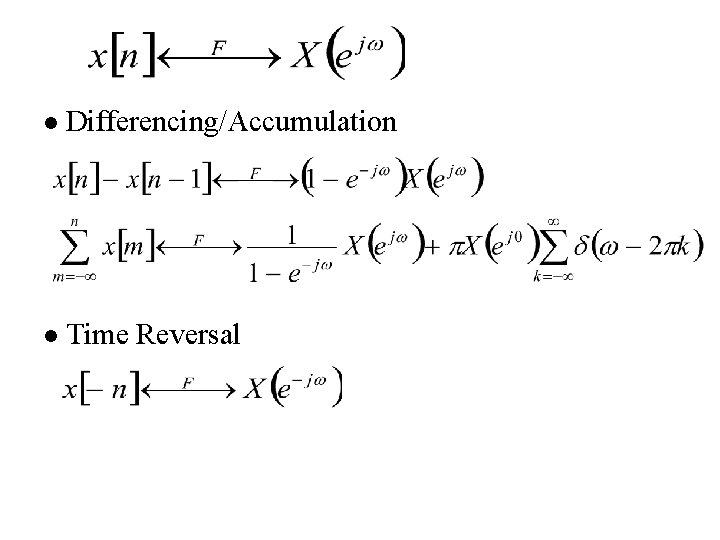
l Differencing/Accumulation l Time Reversal

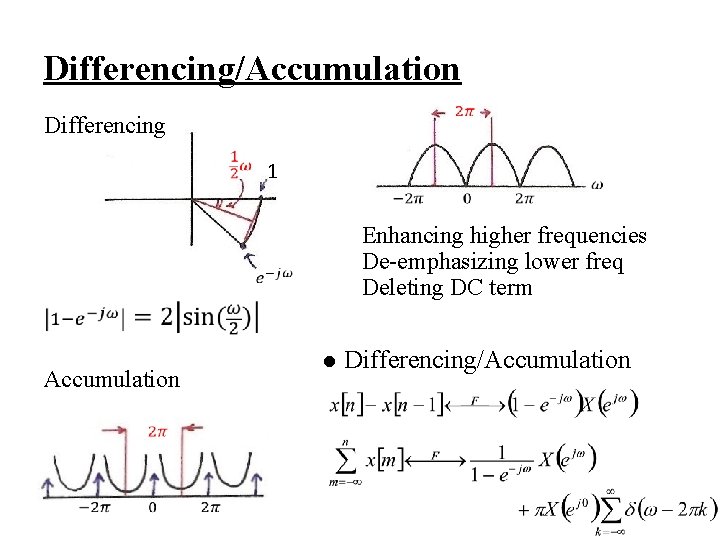
Differentiation (p. 35 of 4. 0) Enhancing higher frequencies De-emphasizing lower frequencies Deleting DC term ( =0 for ω=0)

Integration (p. 36 of 4. 0) dc term Enhancing lower frequencies (accumulation effect) De-emphasizing higher frequencies Accumulation (smoothing effect) Undefined for ω=0

Differencing/Accumulation Differencing 1 Enhancing higher frequencies De-emphasizing lower freq Deleting DC term Accumulation l Differencing/Accumulation

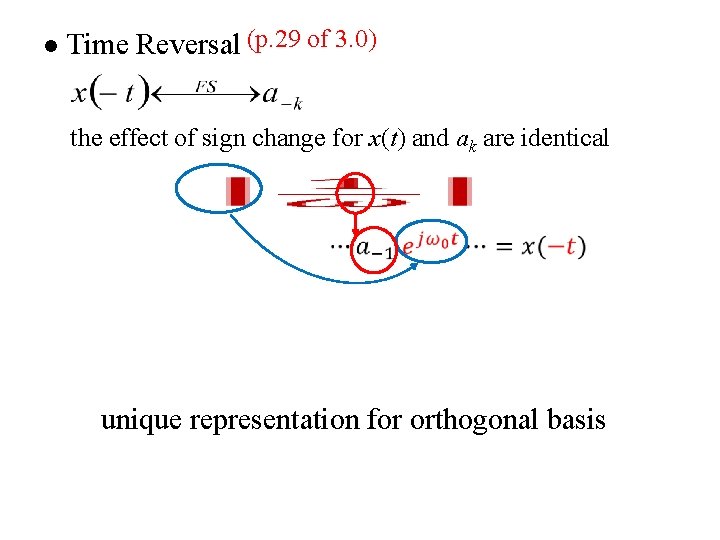
l Time Reversal (p. 29 of 3. 0) the effect of sign change for x(t) and ak are identical unique representation for orthogonal basis
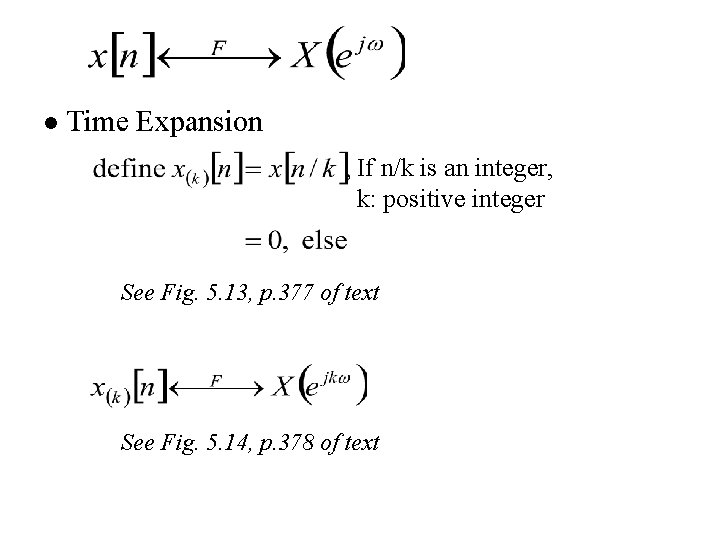
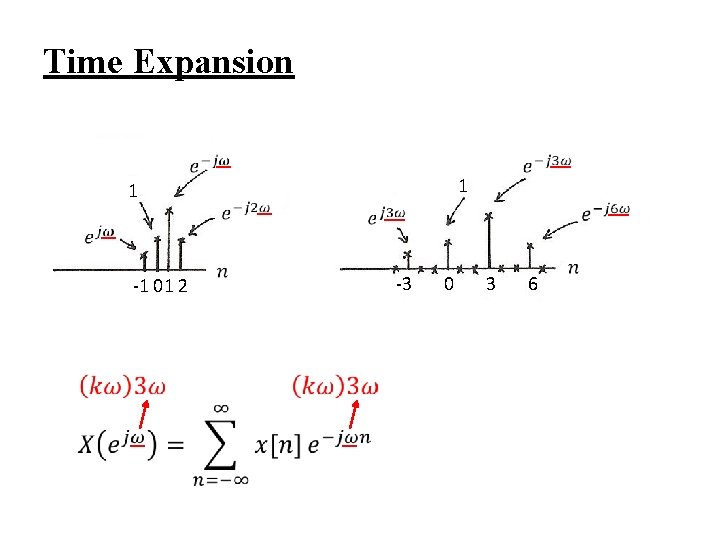
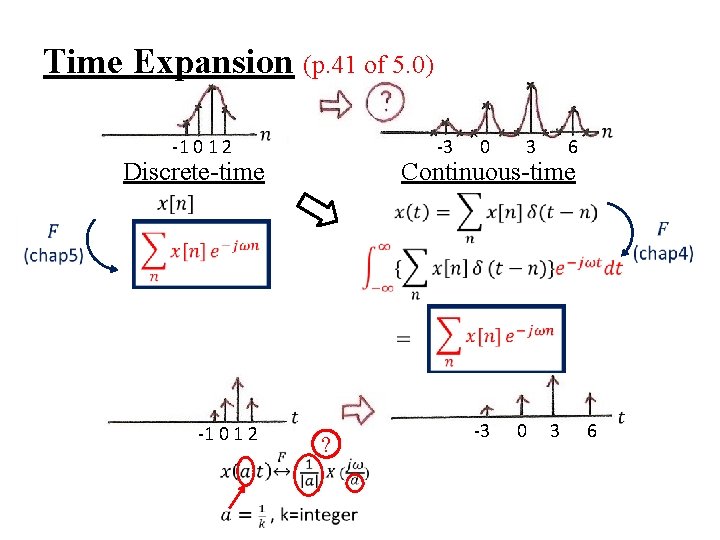
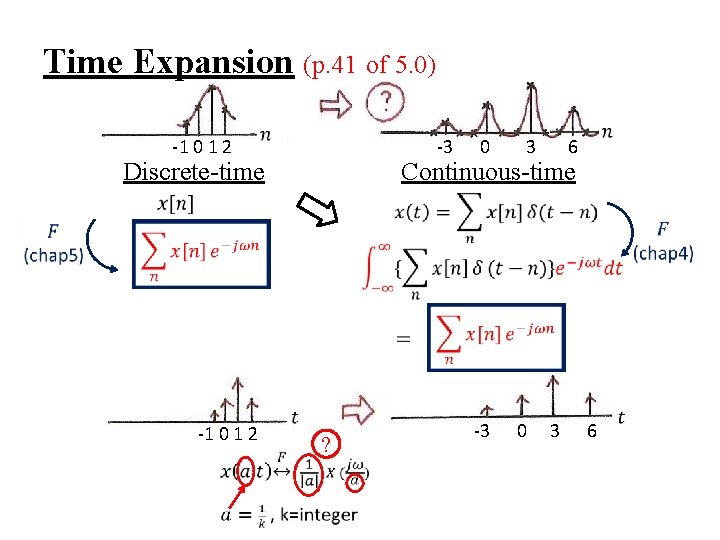
l Time Expansion If n/k is an integer, k: positive integer See Fig. 5. 13, p. 377 of text See Fig. 5. 14, p. 378 of text



Time Expansion 1 1 -1 01 2 -3 0 3 6

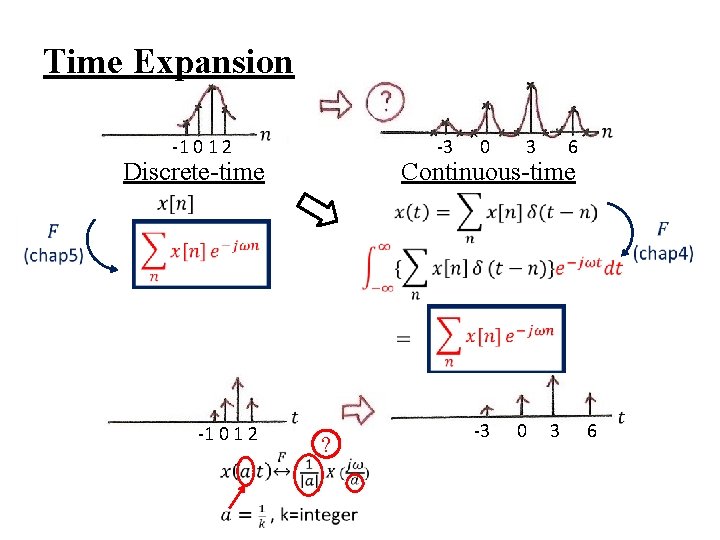
Time Expansion -3 -1 0 1 2 Discrete-time -1 0 1 2 0 3 6 Continuous-time ? -3 0 3 6

l Differentiation in Frequency l Parseval’s Relation

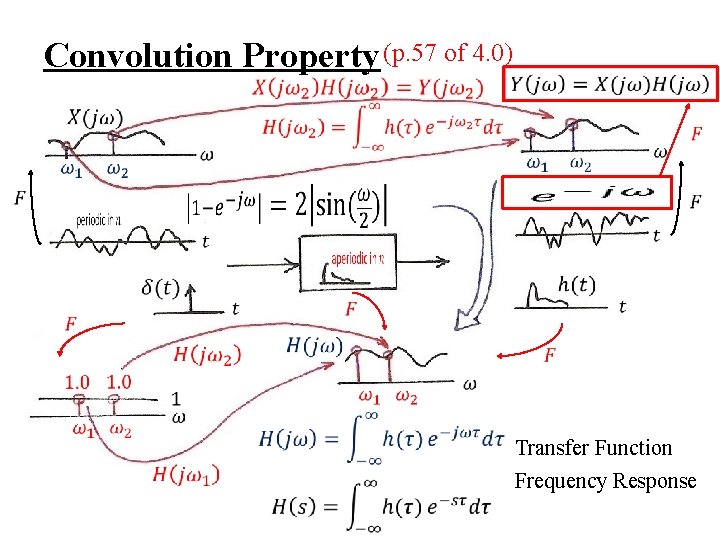
l Convolution Property frequency response or transfer function l Multiplication Property periodic convolution

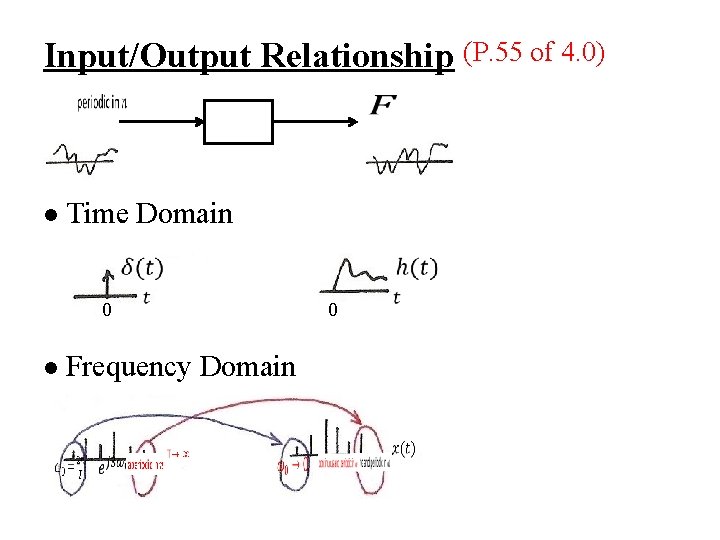
Input/Output Relationship (P. 55 of 4. 0) l Time Domain 0 l Frequency Domain 0

Convolution Property (p. 57 of 4. 0) Transfer Function Frequency Response

l System Characterization l Tables of Properties and Pairs See Table 5. 1, 5. 2, p. 391, 392 of text


![l Vector Space Interpretation xn aperiodic defined on n V is l Vector Space Interpretation {x[n], aperiodic defined on -∞ < n < ∞}=V is](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-51.jpg)
l Vector Space Interpretation {x[n], aperiodic defined on -∞ < n < ∞}=V is a vector space – basis signal sets repeats itself for very 2

l Vector Space Interpretation – Generalized Parseval’s Relation {X(ejω), with period 2π defined on -∞ < ω < ∞}=V : a vector space inner-product can be evaluated in either domain

l Vector Space Interpretation – Orthogonal Bases

l Vector Space Interpretation – Orthogonal Bases Similar to the case of continuous-time Fourier transform. Orthogonal bases but normalized, while makes sense with operational definition.

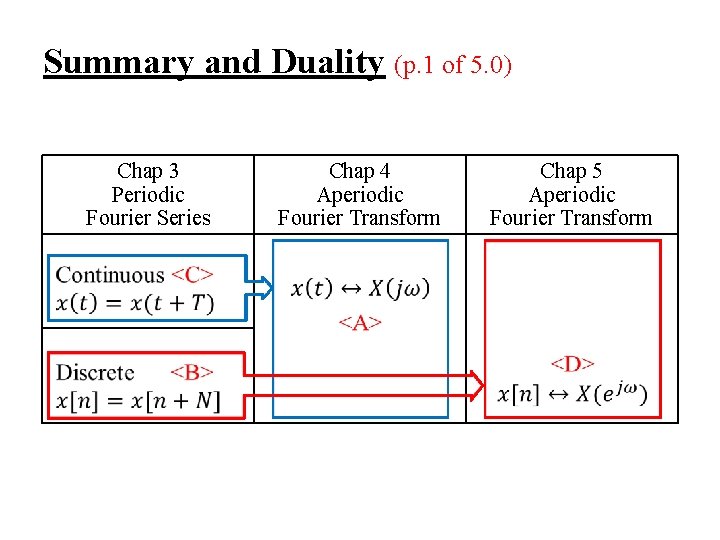
Summary and Duality (p. 1 of 5. 0) Chap 3 Periodic Fourier Series Chap 4 Aperiodic Fourier Transform Chap 5 Aperiodic Fourier Transform

Time Expansion (p. 41 of 5. 0) -3 -1 0 1 2 Discrete-time -1 0 1 2 0 3 6 Continuous-time ? -3 0 3 6

5. 3 Summary and Duality <A> Fourier Transform for Continuous-time Aperiodic Signals (Synthesis) (4. 8) (Analysis) (4. 9) -x(t) : continuous-time (∆t→ 0) aperiodic in time (T→∞) -X(jω) : continuous in frequency(ω0→ 0) aperiodic in frequency(W→∞) Duality<A> :

Case <A> (p. 44 of 4. 0) 0 0
![B Fourier Series for Discretetime Periodic Signals Synthesis 3 94 Analysis 3 95 xn <B> Fourier Series for Discrete-time Periodic Signals (Synthesis) (3. 94) (Analysis) (3. 95) -x[n]](https://slidetodoc.com/presentation_image_h2/6345512068e09c30cbd9d9c822ce3b2b/image-59.jpg)
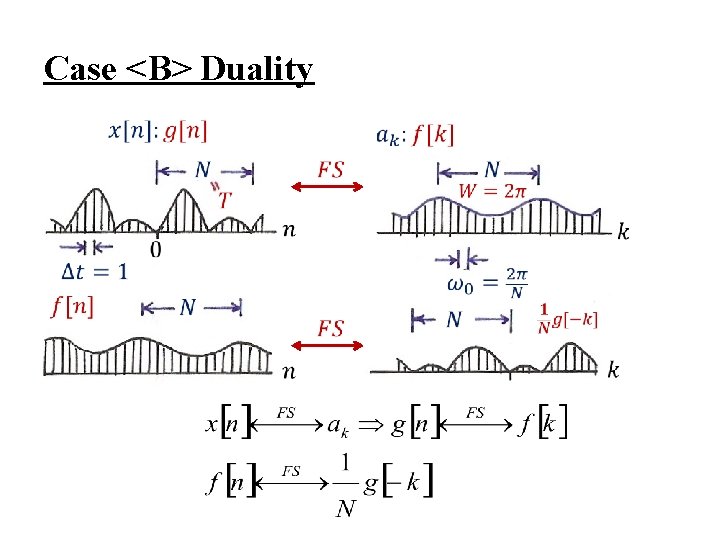
<B> Fourier Series for Discrete-time Periodic Signals (Synthesis) (3. 94) (Analysis) (3. 95) -x[n] : discrete-time (∆t = 1) periodic in time (T = N) -ak : discrete in frequency(ω0 = 2 / N) periodic in frequency(W = 2 ) Duality<B> :

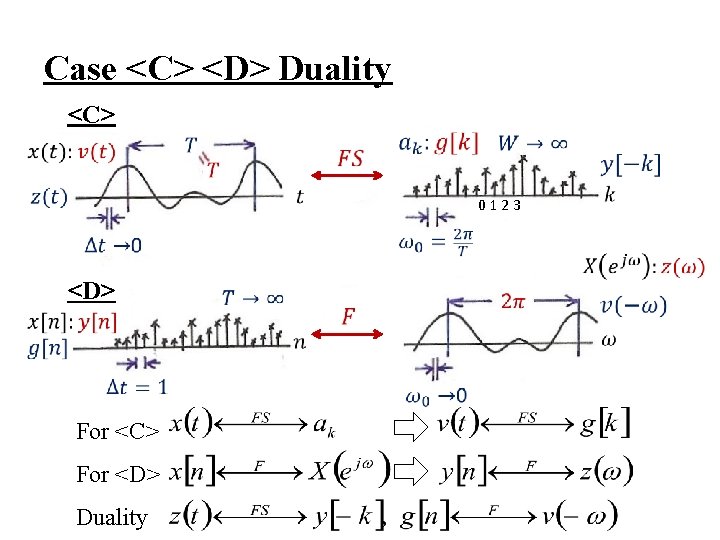
Case <B> Duality

<C> Fourier Series for Continuous-time Periodic Signals (Synthesis) (3. 38) (Analysis) (3. 39) -x(t) : continuous-time (∆t → 0) periodic in time (T = T) -ak : discrete in frequency(ω0 = 2 / T) aperiodic in frequency(W → ∞)

Case <C> <D> Duality <C> 0123 <D> For <C> For <D> Duality

<D> Discrete-time Fourier Transform for Discrete-time Aperiodic Signals (Synthesis) (5. 8) (Analysis) (5. 9) -x[n] : discrete-time (∆t = 1) aperiodic in time (T→∞) -X(ejω) : continuous in frequency(ω0→ 0) periodic in frequency(W = 2 )

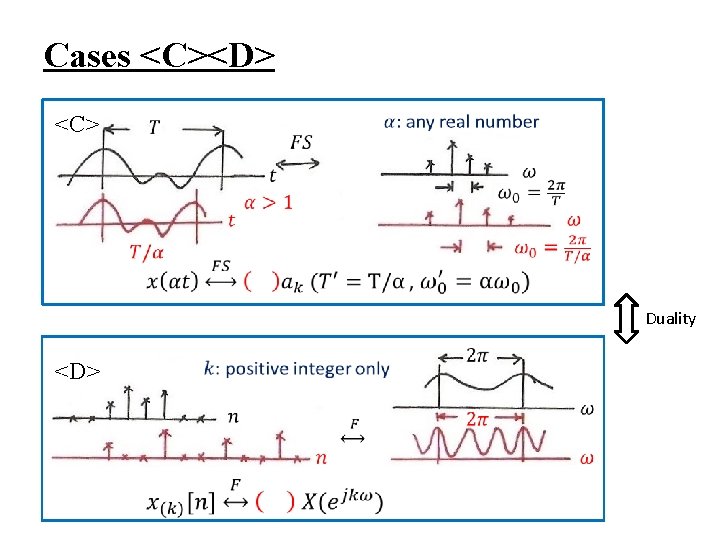
Duality<C> / <D> For <C> For <D> Duality – taking z(t) as a periodic signal in time with period 2 , substituting into (3. 38), ω0 = 1 which is of exactly the same form of (5. 9) except for a sign change, (3. 39) indicates how the coefficients ak are obtained, which is of exactly the same form of (5. 8) except for a sign change, etc. See Table 5. 3, p. 396 of text


l More Duality – Discrete in one domain with ∆ between two values → periodic in the other domain with period – Continuous in one domain (∆ → 0) → aperiodic in the other domain

Harmonically Related Exponentials for Periodic Signals (P. 11 of 3. 0) T • All with period T: integer multiples of ω0 • Discrete in frequency domain

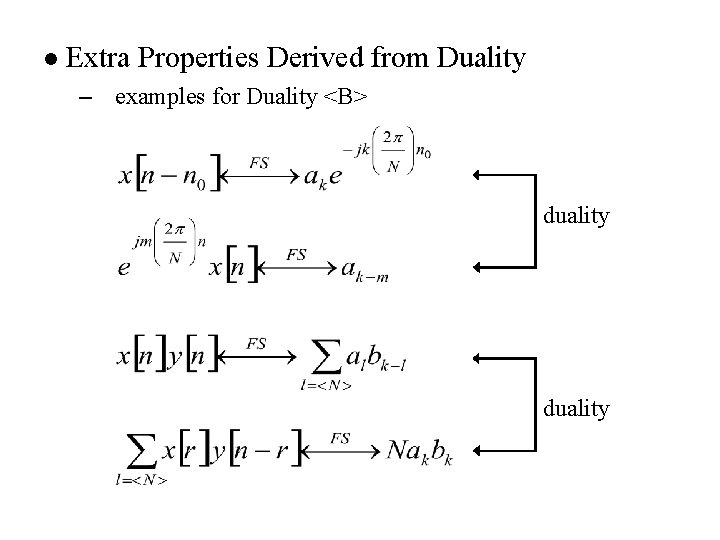
l Extra Properties Derived from Duality – examples for Duality <B> duality

Unified Framework l Fourier Transform : case <A> (4. 8) (4. 9)

Unified Framework l Discrete frequency components for signals periodic in time domain: case <C> you get (3. 38) (applied on (4. 8)) Case <C> is a special case of Case <A>

Unified Framework: Fourier Transform for Periodic Signals (p. 17 of 4. 0) T F S – If F

Unified Framework l Discrete time values with spectra periodic in frequency domain: case <D> (4. 9) becomes (5. 9) Case <D> is a special case of Case <A> Note : ω in rad/sec for continuous-time but in rad for discrete-time

Time Expansion (p. 41 of 5. 0) -3 -1 0 1 2 Discrete-time -1 0 1 2 0 3 6 Continuous-time ? -3 0 3 6

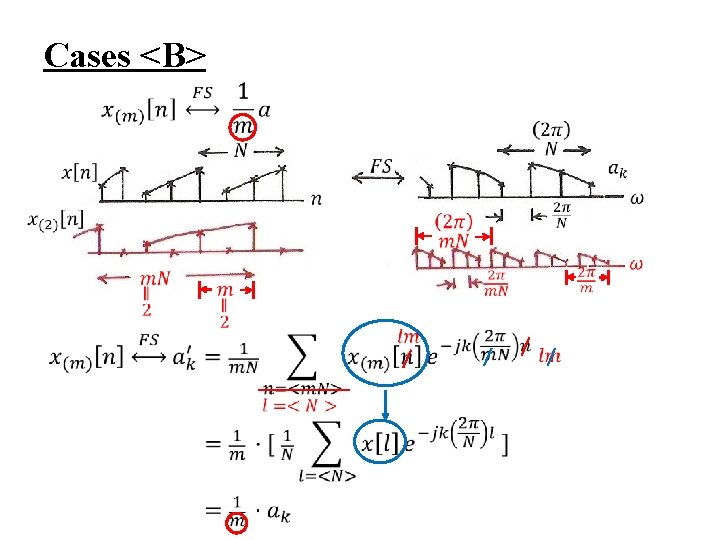
Unified Framework l Both discrete/periodic in time/frequency domain: case <B> -- case <C> plus case <D> periodic and discrete, summation over a period of N (4. 8) becomes (3. 94) (4. 9) becomes (3. 95)

Unified Framework l Cases <B> <C> <D> are special cases of case <A> Dualities <B>, <C>/<D> are special case of Duality <A> l Vector Space Interpretation ----similarly unified

Summary and Duality (p. 1 of 5. 0) Chap 3 Periodic Fourier Series Chap 4 Aperiodic Fourier Transform Chap 5 Aperiodic Fourier Transform

An Example across Cases <A><B><C><D>

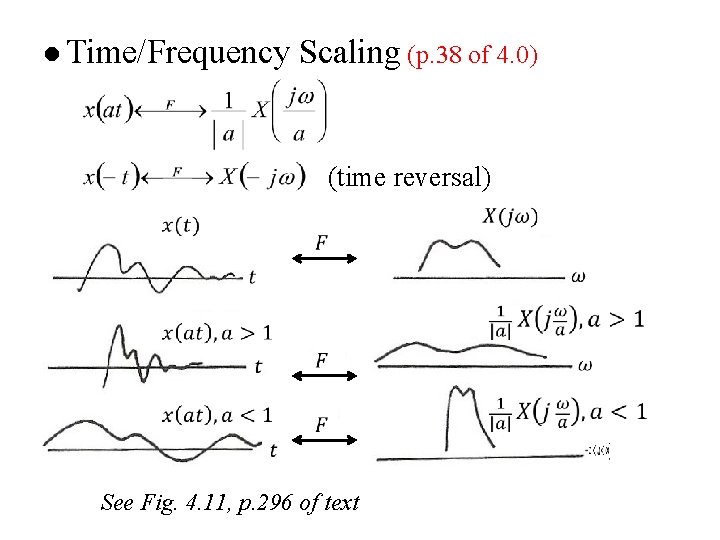
l Time/Frequency Scaling (p. 38 of 4. 0) (time reversal) See Fig. 4. 11, p. 296 of text

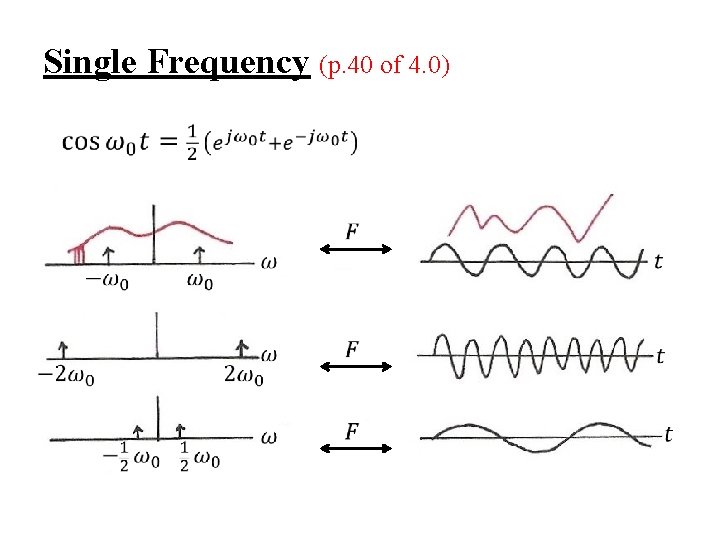
Single Frequency (p. 40 of 4. 0)
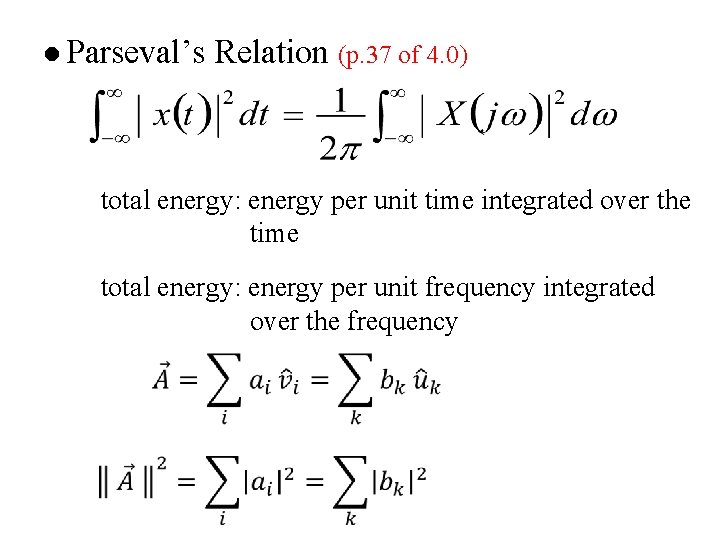
l Parseval’s Relation (p. 37 of 4. 0) total energy: energy per unit time integrated over the time total energy: energy per unit frequency integrated over the frequency

Single Frequency

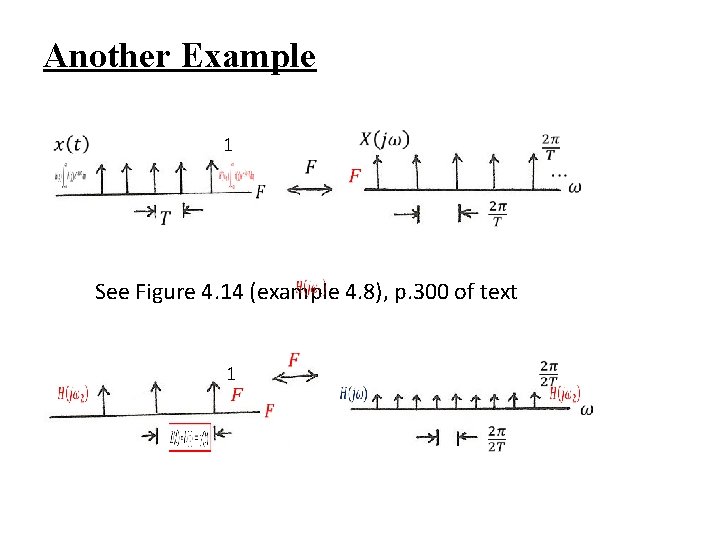
Another Example 1 See Figure 4. 14 (example 4. 8), p. 300 of text 1

Cases <C><D> <C> Duality <D>

Cases <B>

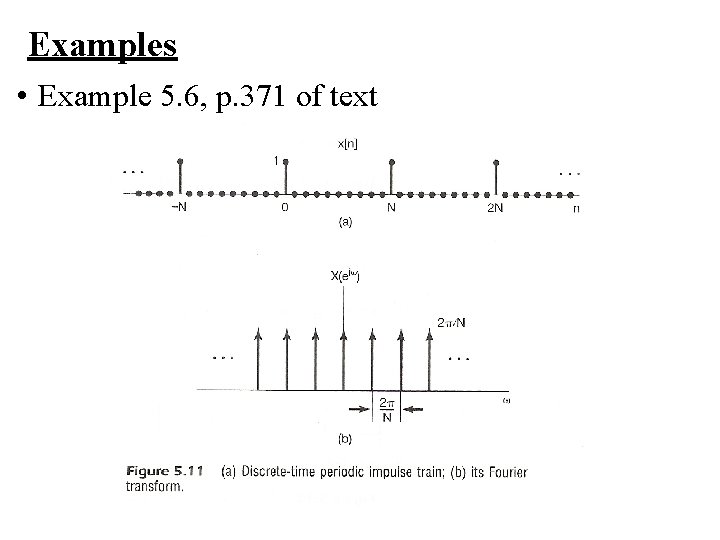
Examples • Example 5. 6, p. 371 of text

Examples • Example 4. 8, p. 299 of text (P. 76 of 4. 0)

Examples • Example 5. 11, p. 383 of text time shift property

Examples • Example 5. 14, p. 387 of text



Examples • Example 5. 17, p. 395 of text

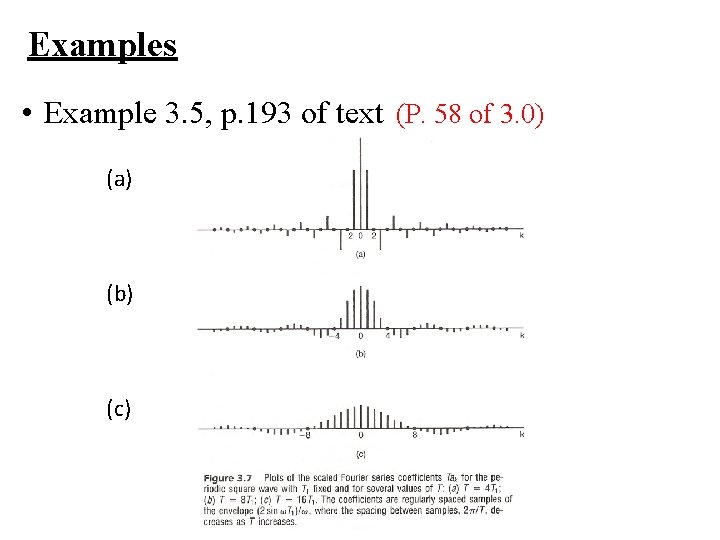
Examples • Example 3. 5, p. 193 of text (P. 58 of 3. 0) (a) (b) (c)

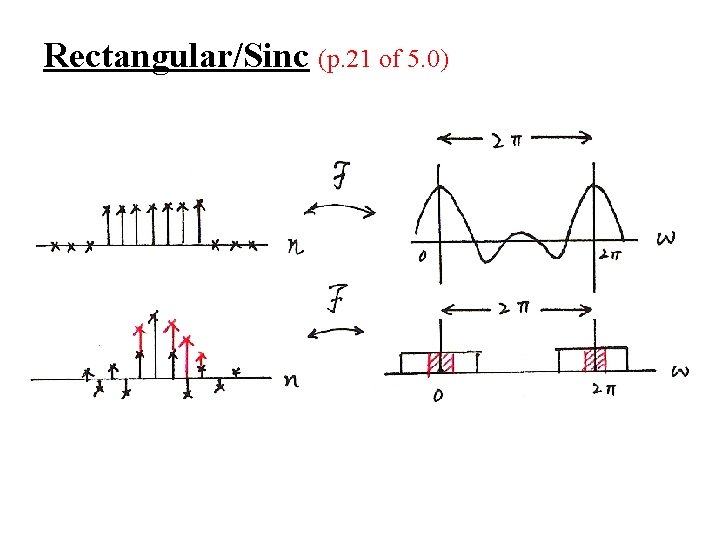
Rectangular/Sinc (p. 21 of 5. 0)

Problem 5. 36(c), p. 411 of text

Problem 5. 43, p. 413 of text

Problem 5. 46, p. 415 of text

Problem 5. 56, p. 422 of text

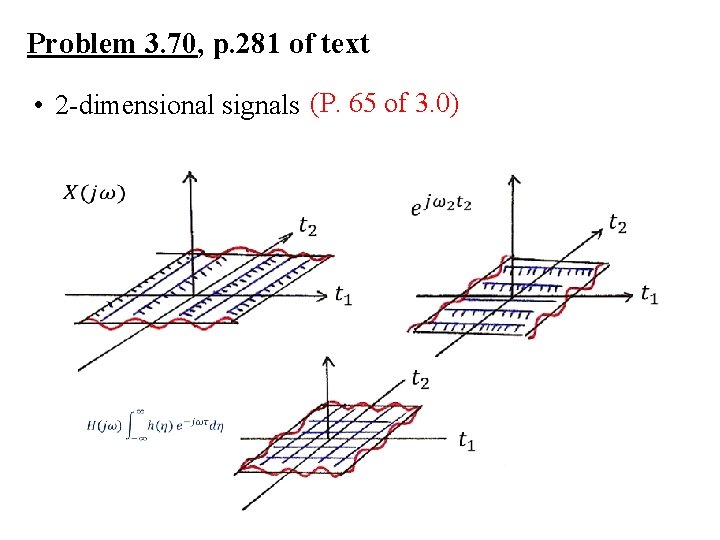
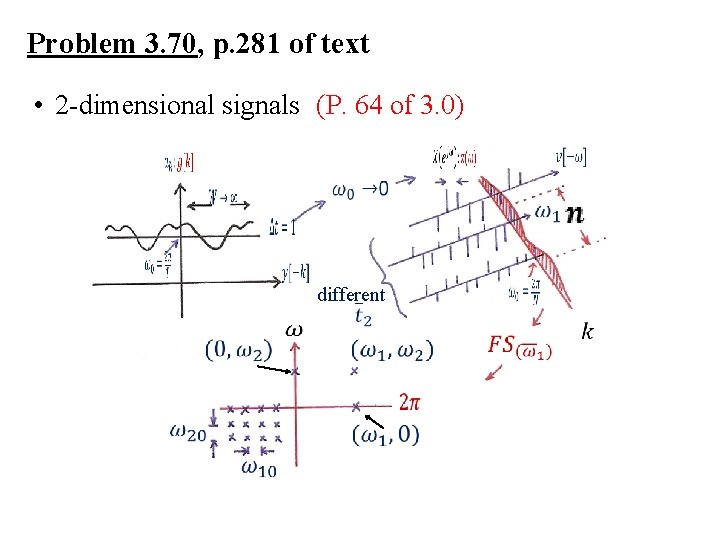
Problem 3. 70, p. 281 of text • 2 -dimensional signals (P. 65 of 3. 0)

Problem 3. 70, p. 281 of text • 2 -dimensional signals (P. 64 of 3. 0) different
 Gaussian fourier transform
Gaussian fourier transform Properties of fourier transform in digital image processing
Properties of fourier transform in digital image processing Inverse of fourier transform
Inverse of fourier transform Discrete fourier transform
Discrete fourier transform Nate conger
Nate conger Synthesis equation fourier series
Synthesis equation fourier series Image processing and analysis stan birchfield pdf
Image processing and analysis stan birchfield pdf Fourier transform
Fourier transform Fourier series half range
Fourier series half range Discrete fourier transform
Discrete fourier transform Duality of fourier transform
Duality of fourier transform Fourier
Fourier Fourier transform of an integral
Fourier transform of an integral Fourier transform seismic
Fourier transform seismic Fourier transform complex analysis
Fourier transform complex analysis Fourier transform pair
Fourier transform pair Frequency
Frequency Relation between laplace and fourier transform
Relation between laplace and fourier transform Find the fourier series of the periodic function
Find the fourier series of the periodic function Inverse fisher transform
Inverse fisher transform Dft table
Dft table Fourier transform formula table
Fourier transform formula table Fourier transform of impulse signal
Fourier transform of impulse signal Laplace transform all formulas
Laplace transform all formulas Fourier transform
Fourier transform 2d discrete fourier transform example
2d discrete fourier transform example Frft meaning
Frft meaning Fourier transformation properties
Fourier transformation properties Chirped pulse fourier transform microwave spectroscopy
Chirped pulse fourier transform microwave spectroscopy Fourier transform formula
Fourier transform formula Phase meaning
Phase meaning R fft
R fft Square wave fourier
Square wave fourier Fourier transform of delta(t-t0)
Fourier transform of delta(t-t0) Windowed fourier transform
Windowed fourier transform Fourier series
Fourier series Overlap save method
Overlap save method Fourier transform is defined for
Fourier transform is defined for Ft representation
Ft representation Short time fourier transform
Short time fourier transform Fourier transform of x
Fourier transform of x Fourier transform definition
Fourier transform definition Fft integer multiplication
Fft integer multiplication Sinc function fourier transform
Sinc function fourier transform Parseval's identity for fourier transform
Parseval's identity for fourier transform Introduction to fast fourier transform
Introduction to fast fourier transform Discrete fourier transform formula
Discrete fourier transform formula Fourier cosine transform of f(x)=1
Fourier cosine transform of f(x)=1 Fourier integral representation
Fourier integral representation Even fourier transform
Even fourier transform Fourier transform
Fourier transform Sinc fourier transform
Sinc fourier transform Fourier transform rules
Fourier transform rules Inverse of fourier transform
Inverse of fourier transform The fourier transform and its applications
The fourier transform and its applications Fourier transform of shifted rectangular pulse
Fourier transform of shifted rectangular pulse Heat equation
Heat equation Forward and inverse fourier transform
Forward and inverse fourier transform Fourier basis
Fourier basis Parseval's identity
Parseval's identity Ctfs fourier
Ctfs fourier Fourier transform
Fourier transform Fft butterfly
Fft butterfly Fourier series formula
Fourier series formula Nstemk
Nstemk Polar fourier series
Polar fourier series Fourier transform of impulse train
Fourier transform of impulse train Linearity property of fourier transform
Linearity property of fourier transform Fourier transform of reciprocal function
Fourier transform of reciprocal function Jpeg fourier transform
Jpeg fourier transform Duality of fourier transform
Duality of fourier transform Fourier transform solver
Fourier transform solver What is dft
What is dft Discrete time fourier transform
Discrete time fourier transform Duality of fourier transform
Duality of fourier transform 4780/2
4780/2 Circ function fourier transform
Circ function fourier transform Fourier transform
Fourier transform Inverse fourier transform formula
Inverse fourier transform formula Application of discrete fourier transform
Application of discrete fourier transform Fourier transform computer vision
Fourier transform computer vision Dft
Dft Fourier transform spherical coordinates
Fourier transform spherical coordinates Matlab ramp function
Matlab ramp function Continuous fourier transform formula
Continuous fourier transform formula Classification of signals
Classification of signals Short time fourier transform applications
Short time fourier transform applications Dirichlet condition for fourier series expansion
Dirichlet condition for fourier series expansion Fast fourier transform
Fast fourier transform Laplace integral transform
Laplace integral transform Orthogonal functions
Orthogonal functions Fourier transform of product of two functions
Fourier transform of product of two functions Discrete time fourier series
Discrete time fourier series Dirichlet condition of fourier series
Dirichlet condition of fourier series Fungsi transformasi fourier
Fungsi transformasi fourier Rumus transformasi fourier
Rumus transformasi fourier Fourier analysis matlab
Fourier analysis matlab Négyszögjel spektruma
Négyszögjel spektruma What is law of heat exchange
What is law of heat exchange Jbj fourier
Jbj fourier