Queueing Theory What is a queue Examples of

Queueing Theory What is a queue? Examples of queues: • Grocery store checkout • Fast food (Mc. Donalds – vs- Wendy’s) • Hospital Emergency rooms • Machines waiting for repair • Communications network

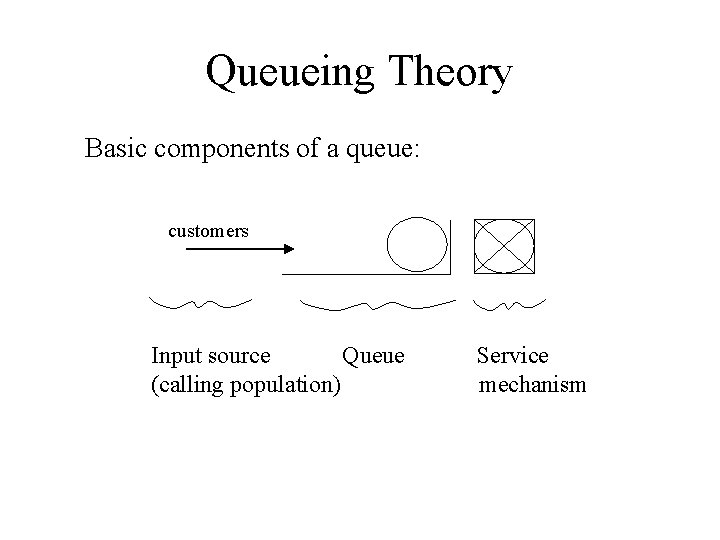
Queueing Theory Basic components of a queue: customers Input source Queue (calling population) Service mechanism

Queueing Theory Queueing System Characteristics Input source: • population size (assumed infinite) • customer generation pattern (assumed Poisson w rate or equivalently, exponential with an inter-arrival time ) • arrival behavior (balking, blocking) Queue: • queue size (finite or infinite) • queue discipline (assumed FIFO, other include random, LIFO, priority, etc. . )

Queueing Theory Service mechanism: • number of servers • service time and distribution (exponential is most common)

Queueing Theory Naming convention: a/b/c/d/e/f a – distribution of inter-arrival times b – distribution of service time c – number of servers Where M – exponential distribution (Markovian) D – degenerate distribution (constant times) Ek – Erlang distribution (with shape k) G = general distribuiton Ex. M/M/1 or M/G/1

Queueing Theory Naming convention cont. : a/b/c/d/e/f d – capacity of the system (default – infinite) e – size of the calling population (default – infinite) f – queue discipline Where FIFO – first in, first out LIFO – last in, first out Random – random selection Ex. M/D/1/inf. /20/LIFO

Queueing Theory Terminology and Notation: State of system – number of customers in the queueing system, N(t) Queue length – number of customer waiting in the queue - state of system minus number being served Pn(t) – probability exactly n customers in system at time t. [pi] s – number of servers [c] ln – mean arrival rate (expected arrivals per unit time) when n customers already in system mn – mean service rate for overall system (expected number of customers completing service per unit time) when n customers are in the system. r – utilization factor (= l/sm , in general)

Queueing Theory Terminology and Notation: L = expected number of customers in queueing system = Lq = expected queue length = W = expected waiting time in system (includes service time) Wq = expected waiting time in queue

Queueing Theory Little’s Law: W=L/l and Wq = L q / l Note: if ln are not equal, then l = Wq + 1/m l when m is constant.

Role of Exponential Distribution Let T be a random variable representing the inter-arrival time between events. f. T(t) a Property 1: f. T(t) is a strictly decreasing function of t (t > 0). P[0 < T < ] > P[t < T < t + t ] P[0 < T < 1/2 a] =. 393 P[1/2 a < T < 3/2 a] =. 383 f. T(t) = ae-at for t > = 0 FT = 1 - e-at E(T) = 1/a Property 2: lack of memory. P[T > t + |T> ] = P[T > t] V (T) = 1/a 2

Role of Exponential Distribution Property 3: the minimum of several independent exponential random variables has an exponential distribution. Let T 1, T 2, …. Tn be distributed exponential with parameters a 1, a 2, …, an and let U = min{T 1, T 2, …. Tn } then: U is exponential with rate parameter a = Property 4: Relationship to Poisson distribution. Let the time between events be distributed exponentially with Parameter a. Then the number of times, X(t), this event occurs over some time t has a Poisson distribution with rate at: P[X(t) = n] = (at)ne-at/n!

Role of Exponential Distribution Property 5: For all positive values of t, P[T < t + for small | T > t] . a can be thought of as the mean rate of occurrence. Property 6: Unaffected by aggregation or dis-aggregation. Suppose a system has multiple input streams (arrivals of customers) with rate l 1, l 2, …ln, then the system as a whole has An input stream with a rate l =

Break for Exercise