Queue ADT Queue ADT Queue is a data

Queue ADT

Queue ADT Queue is a data structure that operates in a FIFO mode First inserted items are removed first Eg. Ticket booking, Printer jobs, FCFS process scheduling, etc en. Queue() - inserts an item into Queue de. Queue() – removes an item from Queue is. Empty. Queue() – checks whether Queue is Empty or not is. Full. Queue() – checks whether Queue is Full or not 11/22/2020 Department of Information Technology , TCE 2

Queue ADT Front = -1 Rear = -1 Front = 0 Rear = 0 Front = 0 Rear = 1 Front = 0 Rear = 2 Front = 0 Rear = 3 10 10 20 20 20 30 30 40 Empty en. Queue(10) en. Queue(20) en. Queue(30) en. Queue(40) en. Queue() again gives Queue Overflow or Queue Full error What is the condition for Queue Full ? 11/22/2020 Department of Information Technology , TCE Rear + 1 == N 3

Queue ADT Assume front and rear are initialized to -1 N is the max size of Queue queue[N] holds the items in the list void en. Queue(int x) begin if (rear < N -1 ) increment rear by 1; queue[rear] = x; return; else return Overflow error; end 11/22/2020 int is. Full. Queue() begin if ( (rear + 1) == N ) return 1; else return 0; // not full end void en. Queue(int x) begin if ( ! is. Full. Queue() ) increment rear by 1; queue[rear] = x; return; else return error; end, TCE Department of Information Technology 4

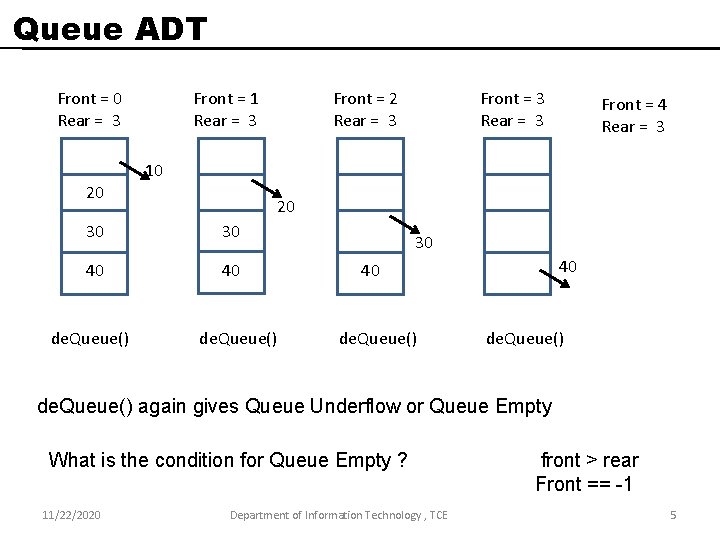
Queue ADT Front = 0 Rear = 3 20 Front = 3 Rear = 3 Front = 4 Rear = 3 10 20 30 30 40 40 de. Queue() Front = 2 Rear = 3 Front = 1 Rear = 3 de. Queue() 30 40 40 de. Queue() again gives Queue Underflow or Queue Empty What is the condition for Queue Empty ? 11/22/2020 Department of Information Technology , TCE front > rear Front == -1 5

Queue ADT Assume front and rear are initialized to -1 N is the max size of Queue queue[N] holds the items in the list int de. Queue() begin int x; if ( front != -1 && front < = rear) x = queue[front]; increment front by 1; return x; else return Underflow error; end 11/22/2020 int is. Empty. Queue() begin if ( ? ? ) return 1; else return 0; // not empty end Department of Information Technology , TCE 6

Lab experiments Lab 5 – Implementation of Queue using array for simple applications like 1. Let Q contains both negative and positive integers. Split Q such that Q 1 contains positive integers and Q 2 contains negative integers. 2. Let Q contains English alphabets. Split Q such that Q 1 contains vowels and Q 2 contains consonants. 3. Merge Q 1 and Q 2 for (above problem 1) 4. Merge Q 1 and Q 2 for (above problem 2) 11/22/2020 Department of Information Technology , TCE 7