Modles de Markov Cachs Adapt de source glanes

Modèles de Markov Cachés Adapté de source glanées sur l’Internet : Yannis Korilis, Christian St-Jean, Dave De. Barr, Bob Carpenter, Jennifer Chu-Carroll et plusieurs autres

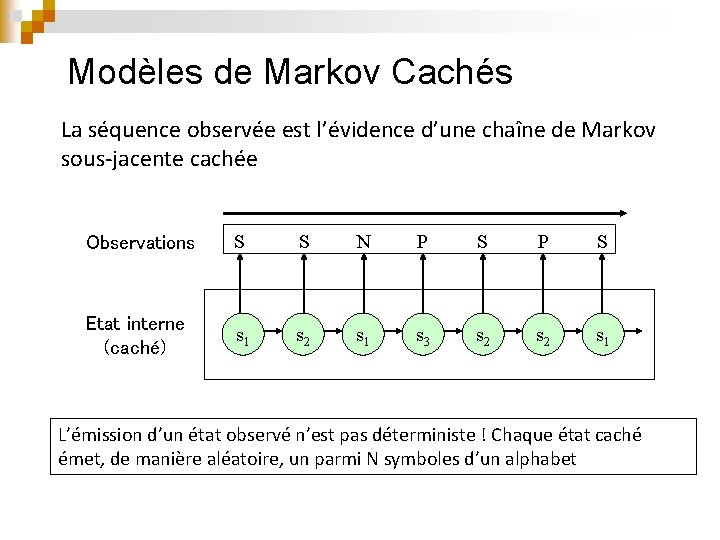
Modèles de Markov Cachés La séquence observée est l’évidence d’une chaîne de Markov sous-jacente cachée Observations S S N P S Etat interne (caché) s 1 s 2 s 1 s 3 s 2 s 1 L’émission d’un état observé n’est pas déterministe ! Chaque état caché émet, de manière aléatoire, un parmi N symboles d’un alphabet

Exemple § Trames sonores représentatives de trois mots différents § pad § bad § spat Mot sous jacent signal sonore observable

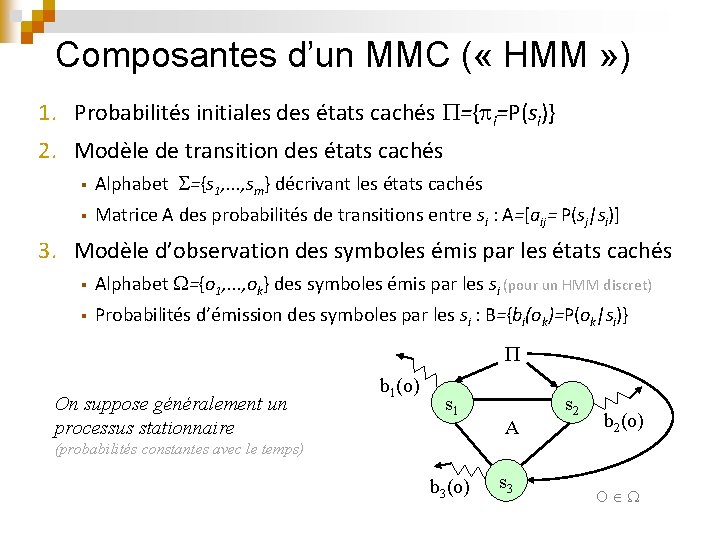
Composantes d’un MMC ( « HMM » ) 1. Probabilités initiales des états cachés ={ i=P(si)} 2. Modèle de transition des états cachés § Alphabet ={s 1, . . . , sm} décrivant les états cachés § Matrice A des probabilités de transitions entre si : A=[aij= P(sj|si)] 3. Modèle d’observation des symboles émis par les états cachés § Alphabet ={o 1, . . . , ok} des symboles émis par les si (pour un HMM discret) § Probabilités d’émission des symboles par les si : B={bi(ok)=P(ok|si)} On suppose généralement un processus stationnaire b 1(o) s 1 A s 2 b 2(o) (probabilités constantes avec le temps) b 3(o) s 3 O

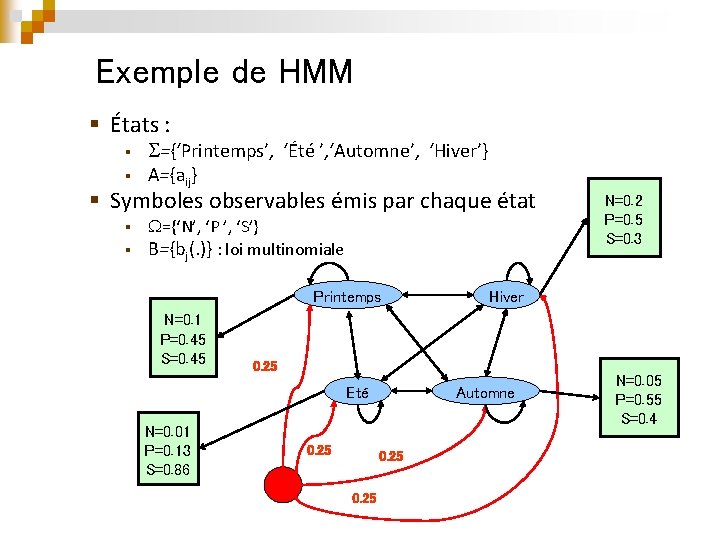
Exemple de HMM § États : § § ={‘Printemps’, ‘Été ’, ‘Automne’, ‘Hiver’} A={aij} § Symboles observables émis par chaque état ={‘N’, ‘P ’, ‘S’} § B={bj(. )} : loi multinomiale § Printemps N=0. 1 P=0. 45 S=0. 45 N=0. 01 P=0. 13 S=0. 86 Hiver 0. 25 Eté 0. 25 Automne 0. 25 N=0. 2 P=0. 5 S=0. 3 N=0. 05 P=0. 55 S=0. 4

Que peut-on faire avec un HMM ? n Évaluation d’un modèle proposé pour expliquer une séquence d’observations n Explication d’une séquence d’observation par un modèle donné n Modélisation d’un processus (caractérisation d’un HMM)

Évaluation de modèle Quel HMM ={ , , , A, B} est le plus probable d’avoir donné lieu à une séquence d’observations O=o 1, . . . , on ? n § Il faut trouver le maximum de P(O| ) : ∙ ∙ Calcul direct Algorithme Forward-Backward

Explication d’une séquence d’observations n Connaissant un HMM , quelle séquence d’états S=s 1, . . . , sn est la plus probable d’avoir donné lieu à une séquence d’observations O=o 1, . . . , on ? } Il faut trouver le maximum de P(S|O, ) : § § Calcul direct L’algorithme de Viterbi

Modélisation (Apprentissage) n Partant d’un ensemble d’observations O, comment régler les paramètres d’un HMM pour maximiser la vraisemblance de P(O| ) ? § § L’entraînement de Viterbi L’algorithme de Baum-Welch

Quelques domaines d’application § Reconnaissance de formes § Reconnaissance de la parole § Traitement de la langue naturelle § Commande automatique § Traitement du signal § Analyse des séquences biologiques § Économie § § Analyse géopolitique Robotique Diagnostic Etc. Avec les SVM, les HMM sont les méthodes statistiques les plus efficaces en dehors des approches neuro-mimétiques

Évaluation de modèle n Étant donné un HMM ={ , , , A, B} , quelle est la probabilité d’occurrence d’une séquence d’observations O, P(O| ) ? Théorème de Bayes Indép. des observations Si Si génère n observations, il faut 2 n-1 multiplications; pour m états possibles, la complexité computationnelle par calcul direct est o(2 n*mn) !

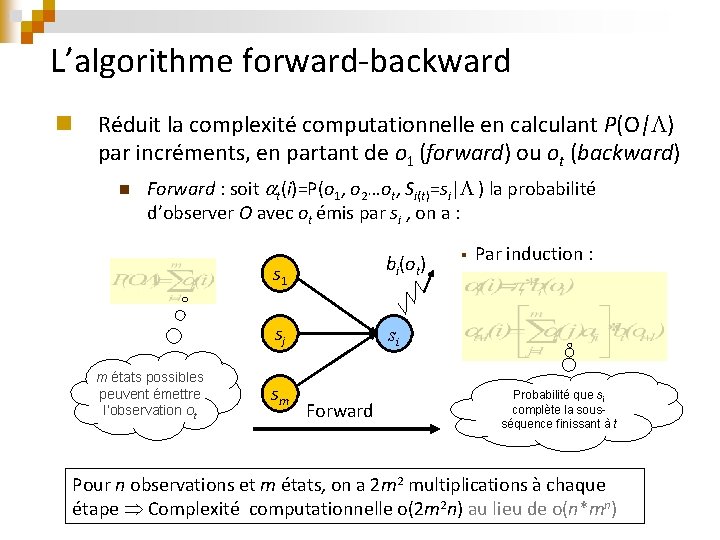
L’algorithme forward-backward n Réduit la complexité computationnelle en calculant P(O| ) par incréments, en partant de o 1 (forward) ou ot (backward) n Forward : soit t(i)=P(o 1, o 2…ot, Si(t)=si| ) la probabilité d’observer O avec ot émis par si , on a : bi(ot) s 1 sj m états possibles peuvent émettre l’observation ot sm § Par induction : si Forward Probabilité que si complète la sousséquence finissant à t Pour n observations et m états, on a 2 m 2 multiplications à chaque étape Complexité computationnelle o(2 m 2 n) au lieu de o(n*mn)

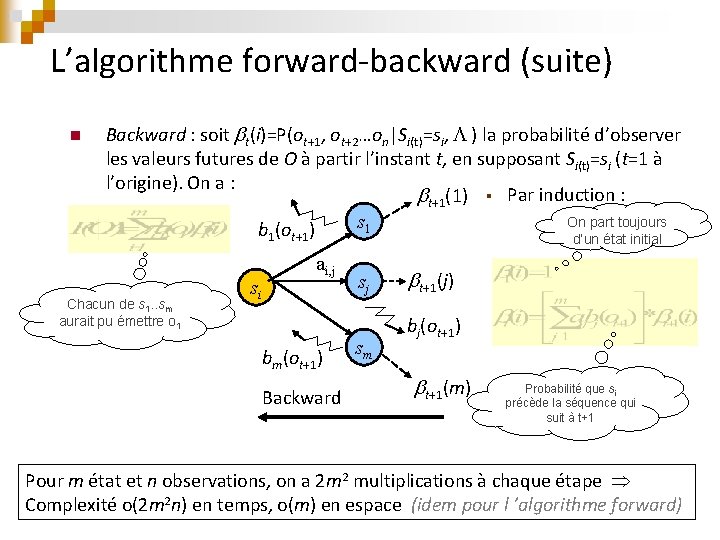
L’algorithme forward-backward (suite) n Backward : soit t(i)=P(ot+1, ot+2…on|Si(t)=si, ) la probabilité d’observer les valeurs futures de O à partir l’instant t, en supposant Si(t)=si (t=1 à l’origine). On a : t+1(1) § Par induction : On part toujours s 1 b (o ) 1 Chacun de s 1. . sm aurait pu émettre o 1 si t+1 d’un état initial ai, j bm(ot+1) Backward sj sm t+1(j) bj(ot+1) t+1(m) Probabilité que si précède la séquence qui suit à t+1 Pour m état et n observations, on a 2 m 2 multiplications à chaque étape Complexité o(2 m 2 n) en temps, o(m) en espace (idem pour l ’algorithme forward)

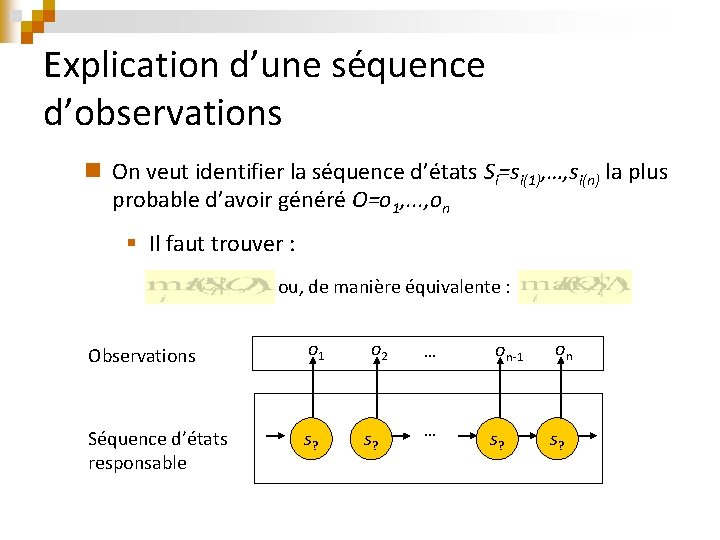
Explication d’une séquence d’observations n On veut identifier la séquence d’états Si=si(1), …, si(n) la plus probable d’avoir généré O=o 1, . . . , on § Il faut trouver : ou, de manière équivalente : Observations o 1 Séquence d’états responsable s? o 2 s? … on-1 on … s?

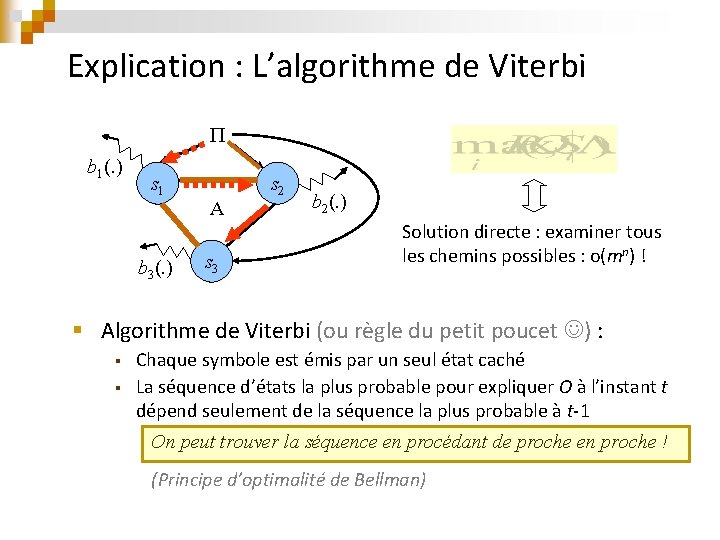
Explication : L’algorithme de Viterbi b 1(. ) s 1 b 3(. ) A s 3 s 2 b 2(. ) Solution directe : examiner tous les chemins possibles : o(mn) ! § Algorithme de Viterbi (ou règle du petit poucet ) : § § Chaque symbole est émis par un seul état caché La séquence d’états la plus probable pour expliquer O à l’instant t dépend seulement de la séquence la plus probable à t-1 On peut trouver la séquence en procédant de proche en proche ! (Principe d’optimalité de Bellman)

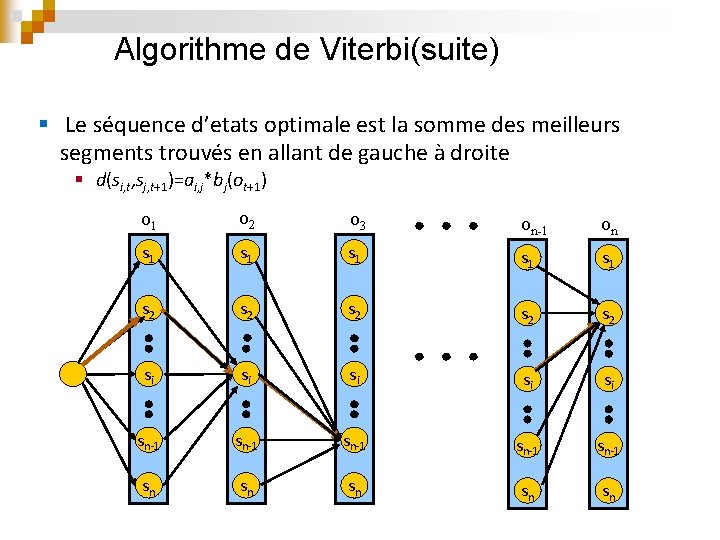
Algorithme de Viterbi(suite) § Le séquence d’etats optimale est la somme des meilleurs segments trouvés en allant de gauche à droite § d(si, t, sj, t+1)=ai, j*bj(ot+1) o 1 o 2 o 3 on-1 on s 1 s 1 s 1 s 2 s 2 s 2 si si si sn-1 sn-1 sn sn sn

Algorithme de Viterbi (fin) § Règle d’induction: § On mémorise, pour chaque t, l’état optimal sj menant à si au temps t+1 On garde trace ainsi des n-1 meilleurs états successifs du parcours Résultat final: Prendre le chemin qui maximise => Complexité en o(m 2*n) en temps, o(m*N) en espace (un chemin par état)

L’algorithme de Viterbi Probabilité du meilleur chemin menant à l’état i au temps t État optimal précédent pour aboutir à l’état i au temps t Meilleur état final Meilleurs états précédents

Exemple § Une personne en vacances envoie une carte postale mentionnant les activités suivantes : § jour 1: plage ; jour 2 : magasinage ; jour 3 : sieste. § On veut en déduire la séquence météorologique sous-jacente probable sachant que : § § Les conditions météorologiques suivent une chaîne de Markov à 2 états : Pluie et soleil On possède des statistiques sur le comportement des touristes selon les états

Modèle HMM ={pluie=1, soleil=2}, ={magasinage=1, plage=2, sieste=3} A = 0. 7 0. 3 0. 4 0. 6 Transition d’états B= 0. 4 0. 3 0. 1 0. 6 = 0. 6 0. 4 0. 5 0. 1 émission de symboles par les état initial § Séquence d’observations : O = 2, 1, 3 § Probabilité du meilleur chemin menant à l’état j au temps t : § État optimal à l’instant t-1 pour aboutir à l’état j au temps t :

Calculs § Étape 1 § Étape § § Observation État 1(1) = π1*b 1(2) = 0. 6*0. 1 = 0. 06, 1(2) = π2*b 2(2) = 0. 4*0. 6 = 0. 24, Ψ 1(1) = Ψ 1(2)=0 § Étape 2 § t = 2 2(1) = maxj ( 1(j)*aj 1)*b 1(1) = max {0. 06*0. 7, 0. 24*0. 4}*0. 4 = 0. 0384 => Ψ 2(1) = argmaxj ( 1(j)*aj 1)= 2 § 2(2) = maxj ( 1(j)*aj 2)*b 2(1) = max{0. 06*0. 3, 0. 24*0. 6}*0. 3 = 0. 0432 => Ψ 2(2) = 2 §

§ t = 3 3(1) = maxj ( 2(j)*aj 1)*b 1(3) = max{0. 0384*0. 7, 0. 0432*0. 4}*0. 5 = 0. 01344 => Ψ 3(1) = 1 § 3(2) = maxj ( 2(j)*aj 2)*b 2(3) = max{0. 0384*0. 3, 0. 0432*0. 6}*0. 1 = 0. 002592 => Ψ 3(2) = 2 § § Étape 3 : s(3) = argmax { 3(1), 3(2)} = 1 § Étape 4 : s(2) = Ψ 3(s(3)) = 1, s(1) = Ψ 2(s(2)) = 2 La séquence d’états cachés la plus probable est 2, 1, 1, avec une vraisemblance P(O|λ) = 0. 01344.

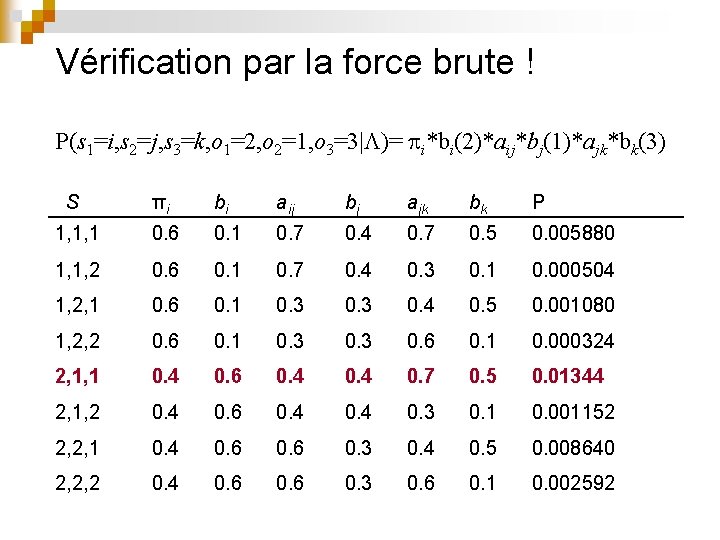
Vérification par la force brute ! P(s 1=i, s 2=j, s 3=k, o 1=2, o 2=1, o 3=3| )= i*bi(2)*aij*bj(1)*ajk*bk(3) S πi bi aij bj ajk bk P 1, 1, 1 0. 6 0. 1 0. 7 0. 4 0. 7 0. 5 0. 005880 1, 1, 2 0. 6 0. 1 0. 7 0. 4 0. 3 0. 1 0. 000504 1, 2, 1 0. 6 0. 1 0. 3 0. 4 0. 5 0. 001080 1, 2, 2 0. 6 0. 1 0. 3 0. 6 0. 1 0. 000324 2, 1, 1 0. 4 0. 6 0. 4 0. 7 0. 5 0. 01344 2, 1, 2 0. 4 0. 6 0. 4 0. 3 0. 1 0. 001152 2, 2, 1 0. 4 0. 6 0. 3 0. 4 0. 5 0. 008640 2, 2, 2 0. 4 0. 6 0. 3 0. 6 0. 1 0. 002592

Caractérisation d’un HMM par apprentissage n Partant d’un ensemble de séquences d’observations O={O 1, . . . , OT}, comment ajuster =< , , , A, B> pour maximiser P(O| ) ? § Choix du nombre d’états § fixé, automatique (critères globaux, fusions d’états) § Choix de la fonction d’émission § loi multinomiale, normale, Student § Méthodes d’apprentissage § Viterbi, Baum-Welch, NN n Une fois spécifié, identifiera la meilleure séquence d’états derrière toute observation O

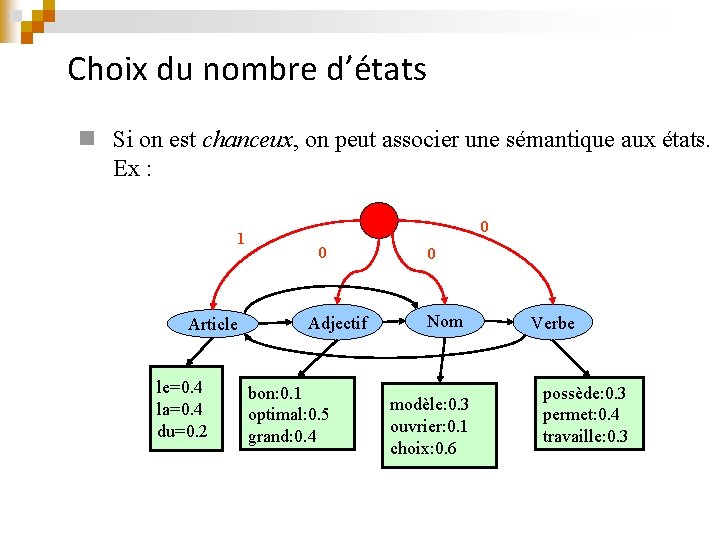
Choix du nombre d’états n Si on est chanceux, on peut associer une sémantique aux états. Ex : 1 Article le=0. 4 la=0. 4 du=0. 2 0 0 Adjectif bon: 0. 1 optimal: 0. 5 grand: 0. 4 0 Nom modèle: 0. 3 ouvrier: 0. 1 choix: 0. 6 Verbe possède: 0. 3 permet: 0. 4 travaille: 0. 3

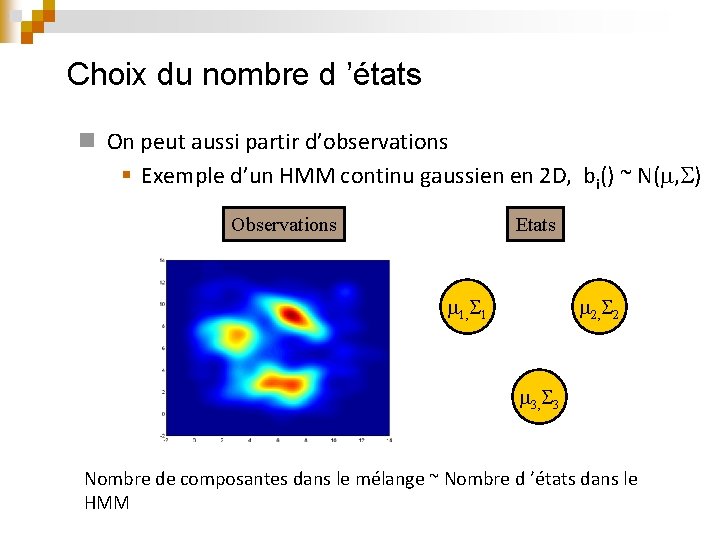
Choix du nombre d ’états n On peut aussi partir d’observations § Exemple d’un HMM continu gaussien en 2 D, bi() ~ N( , ) Observations Etats 1, 1 2, 2 3, 3 Nombre de composantes dans le mélange ~ Nombre d ’états dans le HMM

Entraînement de Viterbi n. On dispose d’un ensemble d’observations O={O 1, . . . , OT} § Principe du max. de vraisemblance: § Max. de vraisemblance suivant les chemins de Viterbi: - Approche moins rigoureuse + Hypothèse de Viterbi: « Tous les autres chemins ont une probabilité nulle ou négligeable » + Algorithme optimal

Entraînement de Viterbi n bj() : loi multinomiale sur l’alphabet Rappel : : Nombre d’émissions de ol par sj pour la séquence Si : Nombre de transitions de sj à sk pour la séquence Si

Entraînement de Viterbi : Nombre de passages sj en sk pour l ’ensemble des séquences : Nombre d’émissions du symbole ol par sj pour l ’ensemble des séquences : Nombre de fois où sj est premier dans le chemin de Viterbi Maximiser cette formule <=> Maximiser les 3 sous-produits

Entraînement de Viterbi 1. Choix du paramétrage initial du HMM 2. Répéter ∙ Initialiser les compteurs à 0 ∙ Pour chaque séquence d’observations Oi ∙ Calculer le chemin de Viterbi pour le HMM courant ∙ Mettre à jour des compteurs Fin pour ∙ Re-estimer les paramètres du HMM avec les formules précédentes Jusqu’à stabilité des paramètres;

Algorithme de Baum-Welch On veut toujours estimer , mais sans connaissance de chemin !! Probabilité dans de passer par si à t et sj à t+1 pour l’a séquence observations Ok : ot+1 Avec la règle de Bayes: si aij sj

Algorithme de Baum-Welch (2) Conséquences pour une séquence d’observations donnée : : Probabilité dans de se retrouver à l’instant t dans l’état si : Espérance du nombre de transitions par sj à l’instant t : Espérance du nombre total de passages par si => on aboutit à des estimateurs simples. . .

Algorithme de Baum-Welch (3) Formules à étendre pour T séquences !

Algorithme de Baum-Welch (fin) ∙ Choix du paramétrage initial du HMM ∙ Répéter ∙ Pour chaque séquence Oi ∙ Calculer avec l ’algorithme forward ∙ Calculer avec l ’algorithme backward ∙ Calculer ∙ Fin pour ∙ Ré estimer les paramètres du HMM avec les formules précédentes ∙ Jusqu ’à stabilité des paramètres; Croissance monotone de la vraisemblance => optimum local