Juros Compostos Disciplina de Matemtica Financeira Extenso Universitria

Juros Compostos Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Conceito de juros compostos Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Conceitos básicos - No sistema de juros compostos (regime de capitalização composta), os juros são calculados sobre o montante, isto é, os juros incidem sobre o valor principal atualizado. - O regime de capitalização composta é usado nas seguintes situações: Ø Ø Correção da poupança; Financiamento habitacional; Financiamento de automóveis; Empréstimos bancários.

Fórmulas de Juros compostos M = Valor Futuro ou Montante C = Valor Presente ou Capital Inicial i = taxa de juros compostos n = número de períodos que o capital ficou aplicado J = juros cobrados ou pagos ou rendimento de uma aplicação

Resumindo. . . JUROS COMPOSTOS Juros Compostos: É o tipo de juros usado. É o “juros sobre juros”. J = P. [(1 + i)n – 1] M = P. (1 + i)n J = juros P = capital inicial (principal) F = montante i = taxa de juros n = prazo (tempo) Exemplo: Calcular o montante de um capital de $100. 000, aplicado por seis meses, à taxa de juros compostos de 2% a. m. F = 100. 000 x (1+0, 02)6 = $ 112. 616, 24

Exemplos 1. Em que prazo um empréstimo de $ 30. 000, 00 pode ser quitado em um único pagamento de $ 51. 310, 18, sabendo-se que a taxa é de 5% a. m. ? 11 meses 2. A que taxa um capital de $ 43. 000, 00 pode ser dobrado em 18 meses? 3, 926% a. m. 3. Uma pessoa empresta 80. 000, 00 hoje para receber 507. 294, 46 no final de dois anos. Calcular as taxas mensal e anual deste empréstimo. 8%a. m. ou 151, 82%a. a. 4. Depois de quanto tempo um capital, aplicado à taxa de 4% a. m. , quadruplica o seu valor? 35, 35 meses 5. Certa aplicação rende 0, 225% a. d. Em que prazo um investidor poderá receber o dobro da sua aplicação? 308, 4 dias

Vamos utilizar as equações do 2º grau para resolver enunciados envolvendo os juros compostos?

Taxas anuais, mensais e diárias Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Taxas de Juros ESPECIFICAÇÃO DAS TAXAS DE JUROS - Taxas Proporcionais (mais empregada com juros simples) - Taxas Equivalentes (taxas que transformam um mesmo P em um mesmo F) - Taxas Nominais (período da taxa difere do da capitalização) - Taxas Efetivas (período da taxa coincide com o da capitalização)

Taxas Equivalentes Taxas referentes a períodos distintos são equivalentes quando produzem o mesmo montante ao final de um determinado tempo, pela aplicação de um mesmo capital inicial. iq = ( 1 + it)q/t – 1 onde índice q significa o que eu quero e t o que tenho.

Observações Ø O termo taxa equivalente está relacionado com juros compostos. Ø No caso de juros simples usamos o conceito de taxa proporcional.

Exemplo 1: Uma taxa de 80% a. a. equivalerá a qual taxa em 200 dias? iq = ( 1 + it)q/t – 1 i 200 = ( 1 + 0, 8)200/360 – 1 i 200 = ( 1, 8)0, 5556 – 1 i 200 = 1, 3862 – 1 i 200 = 0, 3862 = 38, 62%

Exemplo 2: Uma taxa de 50% a. a. equivalerá a qual taxa em 2 meses? iq = ( 1 + it)q/t – 1 i 2 = ( 1 + 0, 5)2/12 – 1 i 2 = ( 1, 5)0, 1667 – 1 i 2 = 1, 0699 – 1 i 2 = 0, 0699 = 6, 99%

Exemplo 3: Uma taxa de 50% a. a. equivalerá a qual taxa em 1 mês? iq = ( 1 + it)q/t – 1 i 1 = ( 1 + 0, 5)1/12 – 1 i 1 = ( 1, 5)0, 08333 – 1 i 1 = 1, 03437 – 1 i 1 = 0, 03437 = 3, 437%

Exemplo 4: Uma taxa de 50% a. a. equivalerá a qual taxa em 1 dia? iq = ( 1 + it)q/t – 1 i 1 = ( 1 + 0, 5)1/360 – 1 i 1 = ( 1, 5)0, 00278 – 1 i 1 = 1, 00113 – 1 i 1 = 0, 00113 = 0, 113%

Exemplo 5: Uma taxa de 50% a. a. equivalerá a qual taxa em 230 dias? iq = ( 1 + it)q/t – 1 i 230 = ( 1 + 0, 5)230/360 – 1 i 230 = ( 1, 5)0, 63889 – 1 i 230 = 1, 2957 – 1 i 230 = 0, 2957 = 29, 57%

Resumindo. . . Taxas de Juros Compostos Equivalentes iq = ( 1 + it ) q/t - 1 iq = Taxa equivalente it = Taxa que eu tenho q = Número de dias da taxa que eu quero t = Número de dias da taxa que eu tenho Exemplo: A taxa de juros de 5% ao trimestre equivale a que taxas anual e mensal? iq = (1+0, 05) 360/90 - 1 0, 2155 ou 21, 55% ao ano iq = (1+0, 05) 30/90 - 1 0, 0164 ou 1, 64% ao mês

Taxas de Juros CONVERSÃO DE PRAZOS REGRA GERAL - Primeiro converta o prazo da operação para número de dias; - Logo após, divida o prazo da operação em dias pelo número de dias do prazo da taxa fornecida ou desejada. EXEMPLOS: n = 68 dias i = 15% ao mês n = 3 meses i = 300% ao ano n = 2 bimestres i = 20% ao semestre Dias Meses n = 68 / 30 = 2, 2667 meses Meses Anos n = 90 / 360 = 0, 25 anos Bimestres Semestres n = 120 / 180 = 0, 6667 semestres

Taxas de Juros PRINCÍPIO DA MATEMÁTICA FINANCEIRA Quando taxa e período estiverem em unidades de tempo diferentes, deve-se converter o prazo.

Valor presente e valor futuro de uma série de pagamentos ou recebimentos Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Anuidades ou Séries DEFINIÇÃO Anuidades, Rendas Certas, Série de Pagamentos Corresponde a toda e qualquer sequência de entradas ou saídas de caixa com o objetivo de amortizar uma dívida ou de capitalizar um montante. 0 1 2 3 4 5 6 7 8 Meses i = 3% mês R$600 R$600

Anuidades ou Séries CLASSIFICAÇÃO DAS SÉRIES 1) Quanto ao Tempo: - Temporária (pagamentos ou recebimentos por tempo determinado) - Infinita (os pagamentos ou recebimentos se perpetuam – ad eternum) 2) Quanto à Periodicidade: - Periódica (intervalo de tempo iguais ou constantes) - Não Periódica (intervalos de tempo variáveis ou irregulares) 3) Quanto ao Valor das Prestações: - Fixos ou Uniformes (todos os valores são iguais) - Variáveis (os valores variam, são distintos) 4) Quanto ao Momento dos Pagamentos: - Antecipadas (o 1 o pagamento ou recebimento está no momento “zero”) - Postecipadas (as prestações ocorrem no final dos períodos)

Anuidades ou Séries SÉRIES UNIFORMES Do ponto de vista de quem vai receber as prestações $600 $600 i = 3% mês Meses 0 1 2 3 4 5 6 7 Do ponto de vista de quem vai pagar as prestações 0 1 2 3 4 5 6 7 8 8 Meses i = 3% mês $600 $600

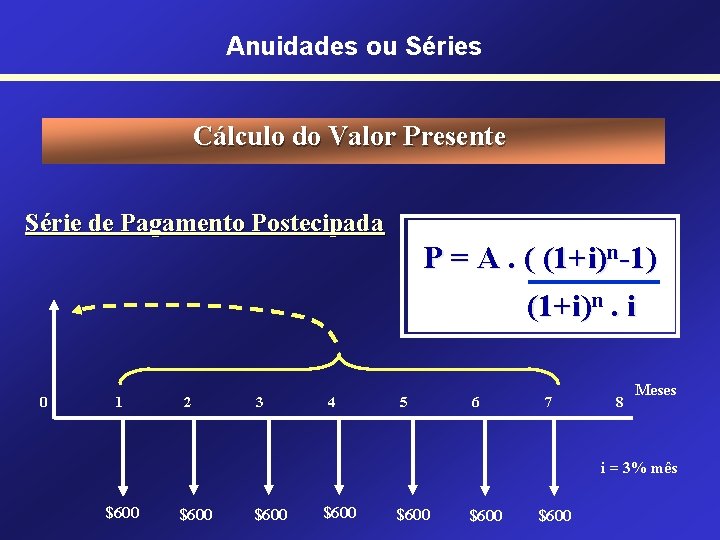
Anuidades ou Séries Cálculo do Valor Presente Série de Pagamento Postecipada P = A. ( (1+i)n-1) (1+i)n. i 0 1 2 3 4 5 6 7 8 Meses i = 3% mês $600 $600

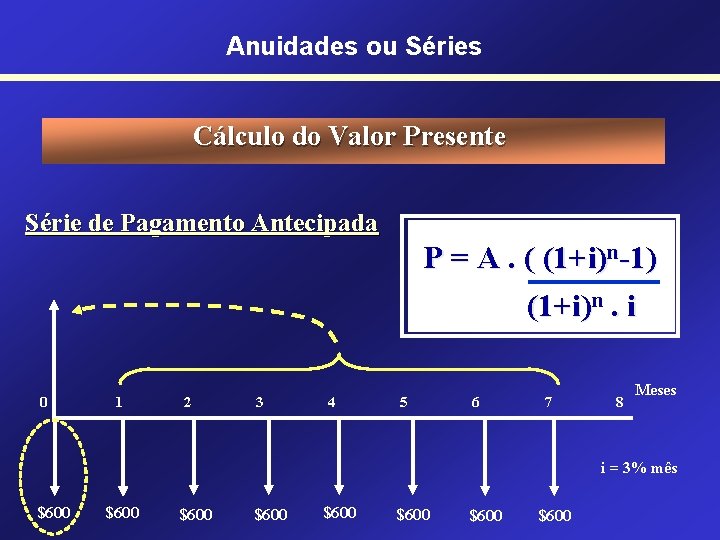
Anuidades ou Séries Cálculo do Valor Presente Série de Pagamento Antecipada P = A. ( (1+i)n-1) (1+i)n. i 0 1 2 3 4 5 6 7 8 Meses i = 3% mês $600 $600

Anuidades ou Séries Exemplo de Série Postecipada 1) Calcular o valor de um financiamento a ser quitado através de seis pagamentos mensais de $1500, vencendo a primeira parcela a 30 dias da liberação dos recursos, sendo de 3, 5% a. m. a taxa de juros negociada na operação. Dados: P = ? n = 6 meses f REG 6 n 1 5 0 i = 3, 5% a. m. A = $1500, 00 g 3 0 END , CHS 5 i PMT PV Resposta: $7. 992, 829530 Série de Pagamento Postecipada

Anuidades ou Séries Exemplo de Série Antecipada 2) Calcular o valor de um financiamento a ser quitado através de quatro pagamentos mensais de $2300, vencendo a primeira parcela no ato da liberação dos recursos, sendo de 4, 2% a. m. a taxa de juros negociada na operação. Dados: P = ? n = 4 meses i = 4, 2% a. m. A = $2300, 00 f REG g 4 n 4 2 3 0 0 BEG , CHS 2 i PMT PV Resposta: $8. 658, 558274 Série de Pagamento Antecipada

Sistemas de amortização Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Amortização Noções Introdutórias Quando um empréstimo é realizado/contraído, o tomador de recursos (pessoa física/jurídica) e o emprestador de recursos (normalmente Banco) combinam de que forma o empréstimo será pago (os recursos devolvidos). Existem várias formas de amortização/pagamento: SAC – Sistema de Amortização Constante; Prestações Constantes ou Método Francês (Price); Sistema Americano.

Amortização Termos Técnicos Ø Capital Financiado Saldo Devedor Inicial Ø Amortizar Pagar/devolver o capital financiado Ø Planilha Conjunto dos dados do contrato de forma sistematizada Ø Desembolso Valor a ser pago pelo devedor (Juros + Capital amortizado + Correção Monetária)

Amortização SISTEMA SAC Características: - A amortização é CONSTANTE (uniforme); - Os juros incidem sobre o saldo devedor (decai com o tempo); - O valor da prestação é decrescente (decai com o tempo). Valor Presente Taxa de juros (i) Amortizações Juros

Amortização SISTEMA DE PRESTAÇÕES CONSTANTES Características: - A amortização é crescente (aumenta com o tempo); - Os juros incidem sobre o saldo devedor (decai com o tempo); - O valor da prestação é CONSTANTE (uniforme). Valor Presente Taxa de juros (i) Juros Amortizações

Amortização SISTEMA AMERICANO Características: - A amortização é paga no final (com a última prestação); - Os juros são constantes (uniforme); - O valor da última prestação difere das demais. Valor Presente Taxa de juros (i) Juros Amortização

Amortização Sistema Americano Com a presença de coupons periódicos (Debêntures)

Valor presente líquido e taxa interna de retorno Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

VPL e TIR O Valor Presente Líquido e a Taxa Interna de Retorno permitem analisar a viabilidade financeira de projetos ou novos negócios, a partir das estimativas dos investimentos iniciais e retornos futuros (fluxos de caixa).

VPL e TIR Outras denominações: Valor Presente Líquido também é conhecido como Valor Atual Líquido, siglas VPL, VAL ou NPV (Net Present Value) Taxa Interna de Retorno também é conhecida pelas siglas TIR ou IRR (Internal Rate of Return)

VPL e TIR como técnicas para avaliação de investimento de capital Ø Ø PAYBACK Simples; PAYBACK Descontado; Valor Presente Líquido (VPL); Taxa Interna de Retorno (TIR) Obs. : Os Paybacks não serão levados em conta em nossos estudos.

Problemas da TIR Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

As desvantagens da metodologia da Taxa Interna de Retorno (TIR) A taxa interna de retorno (TIR) é uma ferramenta útil no arsenal dos analistas financeiros. Entretanto, ela não deve ser utilizada de forma isolada como fator de decisão, uma vez que possui diversas desvantagens.

Definição A taxa interna de retorno é simplesmente o percentual de retorno que um investidor espera obter ao investir em um projeto específico. Se, por exemplo, o investidor espera comprar estoque hoje por R$10 e vendê-lo por R$11 daqui a seis meses, a TIR é de 10% ao semestre. Expressa em base anual, a TIR é de 20%. Em projetos sofisticados, o cálculo se torna bem mais complicado, exigindo uma matemática avançada. Um projeto de construção, por exemplo, pode envolver um desembolso inicial de R$ 5 milhões para compra de terreno e materiais de construção, com gastos adicionais durante a execução, para pagamento dos trabalhadores e compra de mais materiais. Algumas casas podem ser vendidas após 6 meses do início do projeto, com a construção de um decorado para visita de clientes, com vendas adicionais a uma proporção de 1 por mês para o ano seguinte. Estes múltiplos fluxos de caixa fazem com que o cálculo da TIR torne-se difícil de ser feito a mão.

Resultados múltiplos Por mais estranho que possa parecer, é possível encontrar dois valores diferentes para a TIR de um mesmo projeto. Se o investimento produzir diversos fluxos de caixa (entradas e saídas), o cálculo da TIR pode resultar em dois ou mais valores. Esta é uma excentricidade matemática que, embora não seja uma ocorrência frequente, pode confundir significativamente o problema. Se o analista obtém dois resultados e um deles não parece razoável, ele pode optar por aquele que mais se assemelha a de outros projetos similares anteriores. Se os dois resultados estiverem próximos e ambos forem plausíveis, a TIR deverá ser abandonada como ferramenta de decisão.

Risco Enquanto a TIR diz ao analista qual o percentual de retorno de um projeto, ela não informa o risco que o investidor corre para obter tal retorno. Dois projetos podem ter o mesmo fluxo de caixa esperado, com os mesmos prazos. No entanto, as perdas que eles podem causar caso algo dê errado durante o projeto são significativamente diferentes. A TIR não revela as perdas potenciais dos investimentos, mas apenas os retornos esperados. Portanto, ela deve ser utilizada juntamente com medidas de risco, como análise de variância, ou "análise do pior cenário".

Retornos líquidos Um problema adicional com a TIR é que o seu valor não pode ser diretamente traduzido em ganhos líquidos, e nem sempre corresponde aos ganhos líquidos efetivos. Um projeto particular com investimento inicial de R$100. 000 e 20% de TIR anualizada, não resultará necessariamente em um ganho de R$20. 000 ao fim do ano. O projeto pode não manter sua atratividade, durando apenas um mês, e resultando em 1. 6% de ganhos líquidos durante estes 30 dias. Se anualizada, esta taxa corresponde aos 20% ao ano. No entanto, depois de um mês, oportunidades de reinvestimento tão atrativas podem não mais existir, forçando o investidor a depositar seu capital em um banco, a uma taxa bem mais baixa.

Equivalência de taxa de juros Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Mais exercícios. . .

Períodos de capitalização Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

O que é Capitalização? Capitalização é uma maneira de guardar dinheiro com uma vantagem: além de economizar, você concorre a prêmios. Ao final do plano, recebe todo o seu dinheiro de volta corrigido monetariamente. Podem ser feitos depósitos mensais ou um depósito único, com diferentes valores e períodos de duração, que dão direito a sorteios – com prêmios que variam de acordo com o plano escolhido.

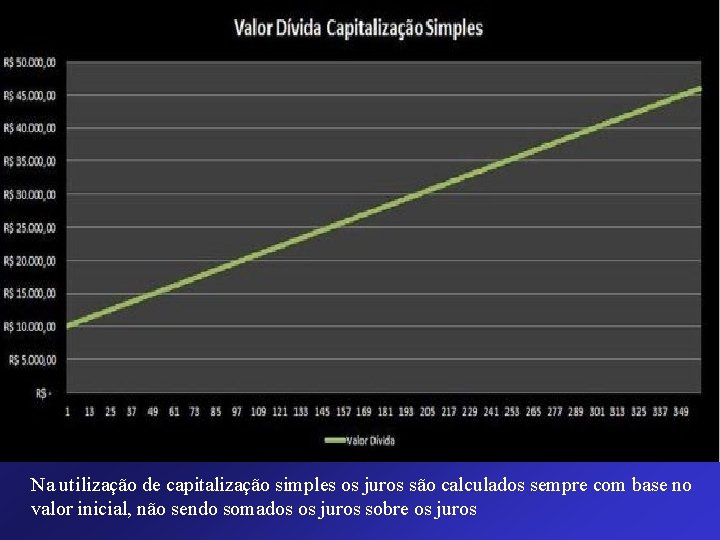
Capitalização Simples (Juros Simples) Quando tratamos de juros simples ou capitalização simples estamos falando sobre os juros que incidem apenas sobre o valor inicial, ou seja, não há a incidência de juros sobre juros. Vamos utilizar como exemplo um empréstimo que você pode fazer a um parente ou amigo, emprestando R$ 10. 000, 00 a uma taxa de 1% ao mês com juros simples. A taxa de juros de 1% será equivalente a quantia de R$100, 00 mensais que irá correr apenas sobre os R$ 10. 000, 00 iniciais. Assim, se o empréstimo levar trinta anos para ser pago e o valor for atualizado utilizando-se juros simples chegaremos a uma quantia de pouco mais de R$ 45. 000, 00. Ao tratarmos de capitalização simples o capital irá crescer de forma linear, em uma linha reta conforme indica o gráfico abaixo:

Na utilização de capitalização simples os juros são calculados sempre com base no valor inicial, não sendo somados os juros sobre os juros.

Capitalização Composta (Juros Compostos) Diferente da capitalização simples, na capitalização composta ou nos juros compostos há a incidência de juros sobre juros (segundo Albert Einstein a maior invenção da humanidade). Nos utilizando do mesmo exemplo utilizado acima onde é concedido um empréstimo a um parente ou amigo, emprestando R$ 10. 000, 00 a uma taxa de 1% ao mês porém agora utilizaremos a capitalização composta. Desta vez então os juros de 1% irão incidir sobre o valor atual da dívida, ou seja, juros sobre juros. Assim, se o empréstimo levar trinta anos para ser pago o valor atualizado será mais de R$ 350. 000, 00. Uma diferença gigantesca não? Ao tratarmos de capitalização composta o capital irá crescer de forma geométrica e o gráfico faz uma forma de parábola onde quanto maior o tempo decorrido, maiores são os juros.

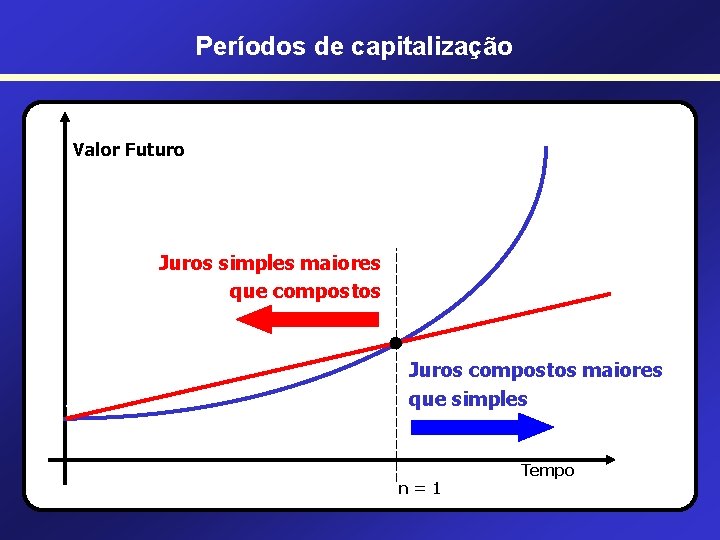
O Valor do Dinheiro no Tempo JUROS SIMPLES x JUROS COMPOSTOS Evolução do Valor Futuro Montante por Juros Compostos CUIDADO: em períodos menores que 1 unidade de tempo, os juros simples dão um montante maior. Montante por Juros Simples Principal 0 0, 5 1 1, 5 n Tempo

Períodos de capitalização JUROS SIMPLES x JUROS COMPOSTOS Antes do primeiro período de capitalização Exemplo: Qual é o montante a ser pago em um empréstimo de $100. 000, pelo prazo de 15 dias, a uma taxa de 30% ao mês? JUROS SIMPLES J=C. i. n J = 100. 0, 3. (15/30) J = $15. 000, 00 F = $115. 000, 00 (montante maior) JUROS COMPOSTOS M = P. (1 + i)n M = 100. 000. (1 + 0, 3)15/30 M = 100. 000. 1, 315/30 > M = $114. 017, 5425 (montante menor) CONCLUSÃO: Antes do primeiro período de capitalização o montante por juros simples é maior do que o obtido por juros compostos.

Períodos de capitalização Valor Futuro Juros simples maiores que compostos • VP Juros compostos maiores que simples n=1 Tempo

Equivalência de fluxos de caixa Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

Diagramas de Fluxo de Caixa CONCEITOS INICIAIS A Matemática Financeira se preocupa com duas variáveis: Dinheiro Tempo

Diagramas de Fluxo de Caixa CONCEITOS INICIAIS As transações financeiras envolvem duas variáveis-chaves: DINHEIRO e TEMPO - Valores somente podem ser comparados se estiverem referenciados na mesma data; - Operações algébricas apenas podem ser executadas com valores referenciados na mesma data.

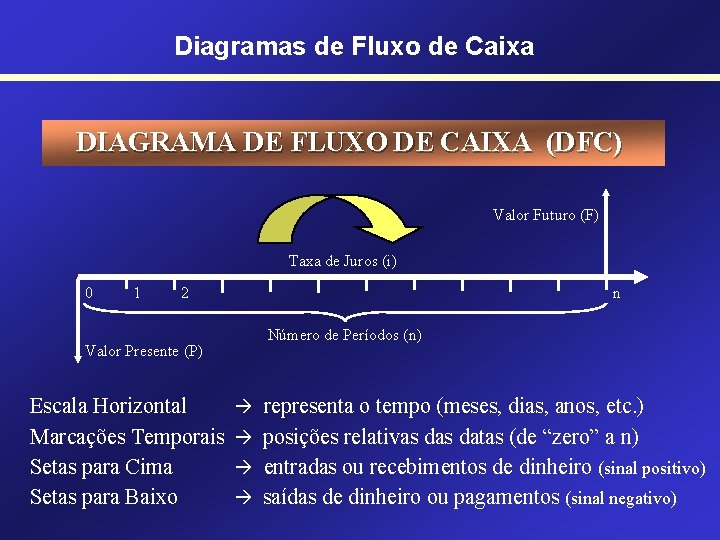
Diagramas de Fluxo de Caixa DIAGRAMA DE FLUXO DE CAIXA (DFC) Desenho esquemático que facilita a representação das operações financeiras e a identificação das variáveis relevantes. Valor Futuro (F) Taxa de Juros (i) 0 1 2 Valor Presente (P) n Número de Períodos (n)

Diagramas de Fluxo de Caixa DIAGRAMA DE FLUXO DE CAIXA (DFC) Valor Futuro (F) Taxa de Juros (i) 0 1 2 Valor Presente (P) Escala Horizontal Marcações Temporais Setas para Cima Setas para Baixo n Número de Períodos (n) representa o tempo (meses, dias, anos, etc. ) posições relativas datas (de “zero” a n) entradas ou recebimentos de dinheiro (sinal positivo) saídas de dinheiro ou pagamentos (sinal negativo)

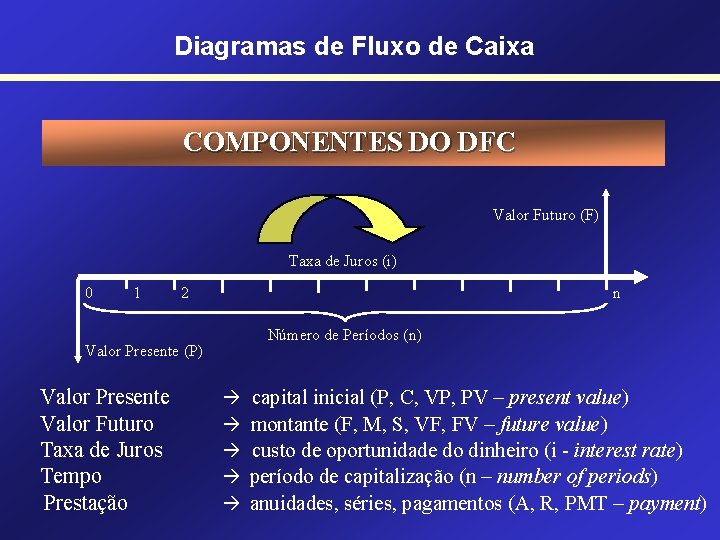
Diagramas de Fluxo de Caixa COMPONENTES DO DFC Valor Futuro (F) Taxa de Juros (i) 0 1 2 Valor Presente (P) Valor Presente Valor Futuro Taxa de Juros Tempo Prestação n Número de Períodos (n) capital inicial (P, C, VP, PV – present value) montante (F, M, S, VF, FV – future value) custo de oportunidade do dinheiro (i - interest rate) período de capitalização (n – number of periods) anuidades, séries, pagamentos (A, R, PMT – payment)

Perpetuidades Disciplina de Matemática Financeira Extensão Universitária em ADMINISTRAÇÃO Prof. Francisco de Paulo Rodrigues Freitas, Esp.

O que são perpetuidades? Falamos em perpetuidade quando temos um pagamento de uma dívida em infinitas prestações. Temos como objetivo calcular o valor de um bem na data zero, ou seja, o valor hoje.

Fórmula O termo perpetuidade (ou série infinita) sugere fluxos de duração infinita sem limite. Entretanto, é mais apropriado dizer que uma perpetuidade se constitui de um conjunto de rendas cujo número não pode ser determinado exatamente, pois é muito grande e tende ao infinito, como sucede, por exemplo, com os dividendos pagos pelas empresas. Assim, quando n é muito grande, tendendo para o infinito, o VP da série se transforma em: VP = R / i , sendo R o valor de cada prestação por período e i a taxa de juros.

EXEMPLOS 1) Um imóvel foi pago perpetuamente com prestações mensais de R$ 1500, 00 a uma taxa de 2 % ao mês. Qual o valor do imóvel? a) 55000, 00 b) 60000, 00 c) 65000, 00 d) 70000, 00 e) 75000, 00 Resolução: Temos que o valor dos pagamentos é de P = 1500. A questão, assim como o assunto, é bem simples: basta utilizarmos a fórmula dada para o valor presente, que é: VP = R / i = 1500 / 0, 02 = 75000 Gabarito: E

2) (Fiscal de Rendas-Sefaz/RJ – FGV – 2009) O valor presente de um título que paga o valor de R$ 500, 00 todo mês, perpetuamente, a uma taxa de juros de 2 %ao mês, no regime de juros compostos, é de: a) R$ 500, 00 b) R$ 5000, 00 c) R$ 50. 000, 00 d) R$ 100. 000, 00 e) R$ 25. 000, 00 Resolução: Mais uma questão “decoreba”… Fazendo VP = R / i , temos: VP = 500 / 0, 02 = 25000 Gabarito: E

• O Obrigado!